人工神经网络及BP算法的理解及如何利用神经网络挑瓜
一. 人工神经网络的理解:
在开始看到人工神经网络时,自以为是很厉害的东西,但随着了解的深入,发现其实也就是那点东西,说白了就是套模板的事。这里要和生物神经网络做区分,虽然人工神经网络也叫神经网络,但其复杂度远不如生物的神经网络,这里是通过代码进行模拟,即并没有创建所谓的神经元,而是用一些参数来假设神经元的存在,例如创建两个神经元之间的的路径的数值及其他特征的数值来模拟神经元的存在.
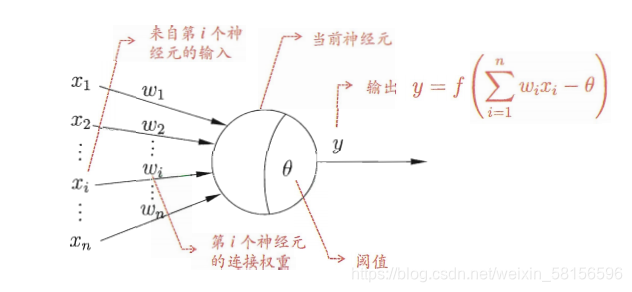
这里将一个神经元看作一个函数,它具有输入和输出。而输入值具有多个,我们对每一个输入值进行一个赋权操作,然后令赋权后值相加,把相加的和与该神经元的阈值做差,将差值作为该神经元的最终的输入,简单来说就是对初始的每一个变量乘一个系数,然后相加。之后把最终的输入值当作自变量,算出该神经元所对应的函数的值,该神经元所对应的函数是人为设定的,一般采用这个函数sidmoid(图像如下)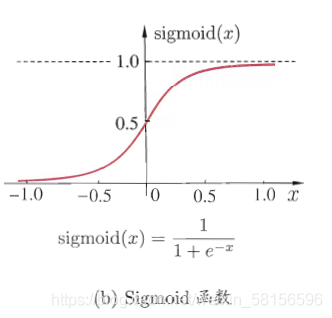
采用这个函数是因为这个函数是连续的,而且具有很好的求导性质,即
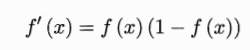
对于之后进行权值和阈值更新比较方便
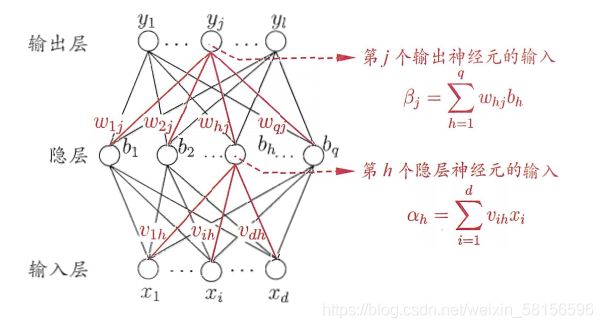
在建立神经网络时,首先建立输入层和输出层,然后根据需要,建立隐层。隐层的数量可以为多层,往往在建立时采用一层隐层,这是因为一层的准确度已经比较高了,采用多层会增加运算上的负担,同时准确率提升不高,当然,也可以不建立隐层,只用输入层和输出层,对于一些简单的处理已经足够了。
以下是两个神经网络图模型:

二. BP算法的理解:
BP算法即误差逆传播算法,先设定神经网络的初始权值和阈值,然后把输入值输入神经网络的输入层,然后令其通过神经网络的处理后得到最终的结果,将这个结果与结果标签进行对比,然后更新这个神经网络的阈值和权值,使得实际的结果去向结果标签靠近。每经过一个样例便进行一次调整,可以认为,当调整的次数足够多时,该神环境网络的阈值和权值已经变得非常理想,此时,该神环境网络的错误率变得非常低,即我们所谓已经训练好的人工智能,我们可以将这个训练好的神环境网络去处理其他数据,进而得出预期的结果。
这里以单个隐层的神经网络为例,假设输出层有L个神经元,我们采用
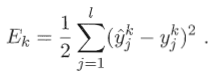
Ek叫做均方误差。
理想话的情况Ek的值为0,然而实际值不为零,则实际值与与预期值的差即为Ek,通过该值去调整权值和阈值。
三. 5.13公式的推导:
这里进行资料5.13式的推导,先给出已经推导好的公式
输出层第J个神经元的阈值

元的输出。


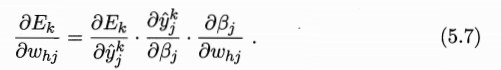

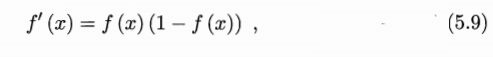
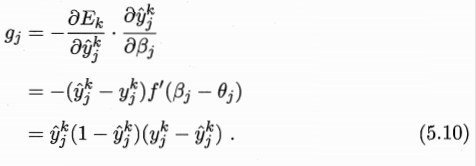

基于上述推导,我们推导
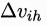
根据定义可知:
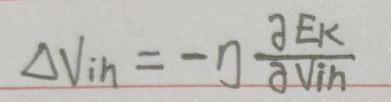
其中:

我们对这三个分别求:
首先:
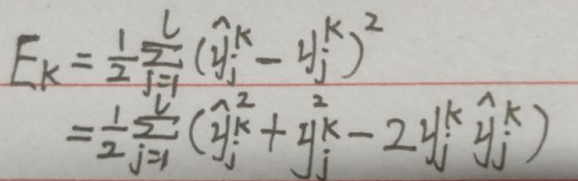

则:
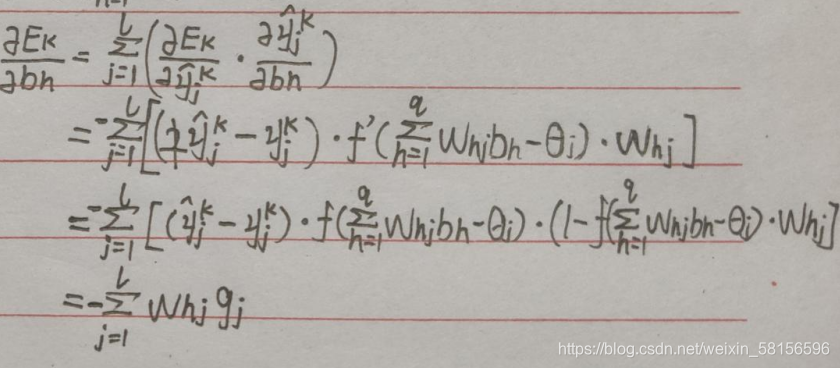
gi为之前已经推导出的
之后求第二个:
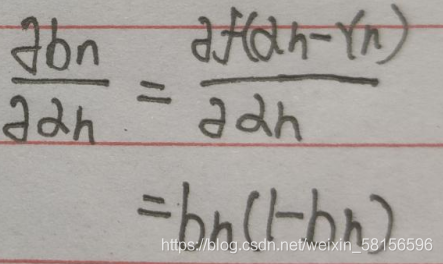
这里用到了:
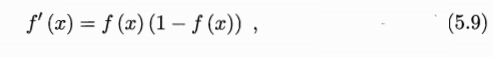
再求最后一项:
这个比较简单:
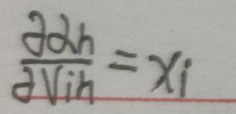
综上:
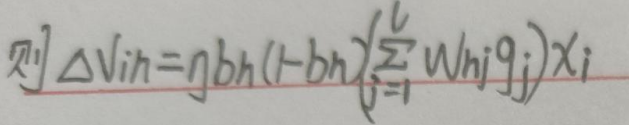
四. 模板代码:
import numpy as np
from numpy.core.fromnumeric import put
from numpy.lib.function_base import append
import pandas as pd
from pandas.core.construction import array
from sklearn import preprocessing
# 设置文本标签转数字程序
trans1 = preprocessing.LabelEncoder()
trans2 = preprocessing.LabelEncoder()
trans1 = trans1.fit([
"青绿", "乌黑", "浅白", "蜷缩", "稍蜷", "硬挺",
"浊响", "沉闷", "清脆",
"清晰", "稍糊", "模糊", "浊响",
"平坦", "凹陷", "稍凹",
"硬滑", "软粘"
])
trans2 = trans2.fit(["是", "否"])
# 加载数据
def loaddataset(path):
# path = "C:\\Users\\小白白\\Desktop\\names.txt"
file = open(path, "r", encoding="utf8")
# 存放数据
dataset = np.array([])
# 存放标签
labelset = np.array([])
for i in file.readlines():
a = i.strip().split(",")
temp = []
temp.extend(a[1:-3])
temp = trans1.transform(temp)
temp = np.append(temp, a[-2])
temp = np.append(temp, a[-3])
dataset = np.append(dataset, temp)
p = np.array([])
p = np.append(p, a[-1])
p = trans2.transform(p)
labelset = np.append(labelset, p)
# 每个数据行的最后一个是标签
dataset = dataset.reshape((17, 8))
file.close()
return dataset, labelset
def parameter_initialization(x, y, z):
# 隐层阈值
value1 = np.random.randint(-5, 5, (1, y)).astype(np.float64)
# 输出层阈值
value2 = np.random.randint(-5, 5, (1, z)).astype(np.float64)
# 输入层与隐层的连接权重
weight1 = np.random.randint(-5, 5, (x, y)).astype(np.float64)
# 隐层与输出层的连接权重
weight2 = np.random.randint(-5, 5, (y, z)).astype(np.float64)
'''value1=np.ones((1,8))
value2=np.ones((1,1))
weight1=np.ones((8,8))
weight2=np.ones((8,1))'''
return weight1, weight2, value1, value2
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def trainning(dataset, labelset, weight1, weight2, value1, value2):
# x为步长
x = 0.1
for i in range(len(dataset)):
# 输入数据
inputset = np.mat(dataset[i]).astype(np.float64)
# 数据标签
outputset = np.mat(labelset[i]).astype(np.float64)
# 隐层输入
input1 = np.dot(inputset, weight1).astype(np.float64)
# 隐层输出
output2 = sigmoid(input1 - value1).astype(np.float64)
# 输出层输入
input2 = np.dot(output2, weight2).astype(np.float64)
# 输出层输出
output3 = sigmoid(input2 - value2).astype(np.float64)
# 更新公式由矩阵运算表示
a = np.multiply(output3, 1 - output3)
g = np.multiply(a, outputset - output3)
b = np.dot(g, np.transpose(weight2))
c = np.multiply(output2, 1 - output2)
e = np.multiply(b, c)
value1_change = -x * e
value2_change = -x * g
weight1_change = x * np.dot(np.transpose(inputset), e)
weight2_change = x * np.dot(np.transpose(output2), g)
# 更新参数
value1 += value1_change
value2 += value2_change
weight1 += weight1_change
weight2 += weight2_change
return weight1, weight2, value1, value2
def testing(dataset, labelset, weight1, weight2, value1, value2):
# 记录预测正确的个数
rightcount = 0
for i in range(len(dataset)):
# 计算每一个样例通过该神经网路后的预测值
inputset = np.mat(dataset[i]).astype(np.float64)
outputset = np.mat(labelset[i]).astype(np.float64)
output2 = sigmoid(np.dot(inputset, weight1) - value1)
output3 = sigmoid(np.dot(output2, weight2) - value2)
# 确定其预测标签
if output3 > 0.5:
flag = 1
else:
flag = 0
if labelset[i] == flag:
rightcount += 1
# 输出预测结果
print("预测为%d 实际为%d" % (flag, labelset[i]))
# 返回正确率
return rightcount / len(dataset)
filename = "C:\\Users\\小白白\\Desktop\\names.txt"
d1, d2 = loaddataset(filename)
w1, w2, v1, v2 = parameter_initialization(len(d1[0]), len(d1[0]), 1)
for i in range(5000):
w1, w2, v1, v2 = trainning(d1, d2, w1, w2, v1, v2)
sum=0
for i in range(10):
sum+=(testing(d1,d2,w1,w2,v1,v2))
print(sum/10.0)
t = int(input("请输入测试样例个数:"))
for i in range(t):
s = input("请按顺序输入西瓜特征:")
s = s.strip().split(",")
temp = []
temp.extend(s[1:-2])
temp = trans1.transform(temp)
temp = np.append(temp, s[-2])
temp = np.append(temp, s[-1])
inputset = np.mat(temp).astype(np.float64)
output2 = sigmoid(np.dot(inputset, w1) - v1)
output3 = sigmoid(np.dot(output2, w2) - v2)
p=""
if output3 > 0.5:
p = "好"
else:
p = "坏"
print("该西瓜判断为%s瓜" % p)
当然,学习率的设置要适当,通常设置为0.1;
学习次数越多,所得的准确率越高
由于初始设定的权值和阈值为随机产生的,所以准确率有一定的浮动,
每次运行程序所得的准确率都不同,但大致在一定范围内,所谓没必要太过计较所造成的偏差。
以下为训练集:
编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否