Bagging集成
- Boostrap抽样
对于线性模型
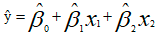
从抽样总体中抽出一个容量为n的样本，通过这n个数据得到参数Beta1的一个估计值。将该过程重复k次（自助采样），可以得到k个Beta1的估计值，利用公式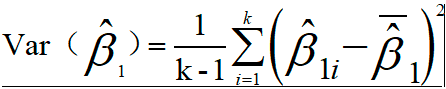
可以求得Beta1的方差，以衡量该线性模型的波动性
- Bagging集成
Bagging集成以boostrap抽样为基础。在得到beta1的k个估计值后，可以通过k个样本集得到k个y的预测值，取k个y的估计值的平均值作为最终预测值。（对于回归问题来说，最终预测值是取k个预测值的平均值，但对于分类问题来说，哪一类的次数出现最多，最终预测值就是哪一类）
作业
1.什么是boostraps？
boostraps是一种通过自助采样来估计模型参数的方差的方法，用于衡量模型的波动性。
2.boostraps与bagging的联系
bagging是以boostraps为基础的集成方法。
4.随机森林与bagging的联系与区别
联系：随机森林与bagging都包含了boostraps的思想
区别：随机森林除了要对样本进行采样外，还要对特征进行采样，与bagging相比，方差进一步减小。
5.使用方差与偏差理论阐述为什么bagging能提升模型的预测精度
测试误差=方差+偏差2，由于bagging中是通过求多个估计值的平均值来作为结果的，故最终结果的方差是σ2/n，是估计值方差的1/n.又因为方差与偏差成反比，当方差减小时，偏差增大，当方差增大时，偏差减小，故最终结果的偏差会增大。但当偏差的增加量小于方差的减小量时，模型的精度会提高。
6.请尝试使用bagging与基本分类模型或回归模型做对比，观察bagging是否相对于基础模型的精度有所提高
参考：
[1]https://github.com/datawhalechina/ensemble-learning
[2]https://www.bilibili.com/video/BV1Mb4y1o7ck?t=360&p=27