建模和评估-建模
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from IPython.display import Image
%matplotlib inline
plt.rcParams['font.sans-serif'] = ['SimHei']#正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False#正常显示负号
plt.rcParams['figure.figsize'] = (10,6)#设置图片大小
train = pd.read_csv('train.csv')
train.shape
(891, 12)
train.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
特征工程
缺失值补充
·分类变量缺失值:用最多的类别填充,用缺失值字符NA填充
·连续变量缺失值:填充均值、中位数、众数
#对分类变量填充
train['Cabin'] = train['Cabin'].fillna('NA')
train['Embarked'] = train['Embarked'].fillna('S')
#连续变量的填充
train['Age'] = train['Age'].fillna(train['Age'].mean())
#检查缺失值比例
train.isnull().sum().sort_values(ascending = False)
PassengerId 0
Survived 0
Pclass 0
Name 0
Sex 0
Age 0
SibSp 0
Parch 0
Ticket 0
Fare 0
Cabin 0
Embarked 0
dtype: int64
#取出输入特征
data = train[['Pclass','Sex','Age','SibSp','Parch','Fare', 'Embarked']]
data
| Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | |
|---|---|---|---|---|---|---|---|
| 0 | 3 | male | 22.000000 | 1 | 0 | 7.2500 | S |
| 1 | 1 | female | 38.000000 | 1 | 0 | 71.2833 | C |
| 2 | 3 | female | 26.000000 | 0 | 0 | 7.9250 | S |
| 3 | 1 | female | 35.000000 | 1 | 0 | 53.1000 | S |
| 4 | 3 | male | 35.000000 | 0 | 0 | 8.0500 | S |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 886 | 2 | male | 27.000000 | 0 | 0 | 13.0000 | S |
| 887 | 1 | female | 19.000000 | 0 | 0 | 30.0000 | S |
| 888 | 3 | female | 29.699118 | 1 | 2 | 23.4500 | S |
| 889 | 1 | male | 26.000000 | 0 | 0 | 30.0000 | C |
| 890 | 3 | male | 32.000000 | 0 | 0 | 7.7500 | Q |
891 rows × 7 columns
train
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.000000 | 1 | 0 | A/5 21171 | 7.2500 | NA | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.000000 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.000000 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NA | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.000000 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.000000 | 0 | 0 | 373450 | 8.0500 | NA | S |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 886 | 887 | 0 | 2 | Montvila, Rev. Juozas | male | 27.000000 | 0 | 0 | 211536 | 13.0000 | NA | S |
| 887 | 888 | 1 | 1 | Graham, Miss. Margaret Edith | female | 19.000000 | 0 | 0 | 112053 | 30.0000 | B42 | S |
| 888 | 889 | 0 | 3 | Johnston, Miss. Catherine Helen "Carrie" | female | 29.699118 | 1 | 2 | W./C. 6607 | 23.4500 | NA | S |
| 889 | 890 | 1 | 1 | Behr, Mr. Karl Howell | male | 26.000000 | 0 | 0 | 111369 | 30.0000 | C148 | C |
| 890 | 891 | 0 | 3 | Dooley, Mr. Patrick | male | 32.000000 | 0 | 0 | 370376 | 7.7500 | NA | Q |
891 rows × 12 columns
比较train和data,我们把train中有用的数据提取出来并汇集到新的数据集data中。
编码分类变量
#虚拟变量转换
data = pd.get_dummies(data)
data
| Pclass | Age | SibSp | Parch | Fare | Sex_female | Sex_male | Embarked_C | Embarked_Q | Embarked_S | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 22.000000 | 1 | 0 | 7.2500 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 38.000000 | 1 | 0 | 71.2833 | 1 | 0 | 1 | 0 | 0 |
| 2 | 3 | 26.000000 | 0 | 0 | 7.9250 | 1 | 0 | 0 | 0 | 1 |
| 3 | 1 | 35.000000 | 1 | 0 | 53.1000 | 1 | 0 | 0 | 0 | 1 |
| 4 | 3 | 35.000000 | 0 | 0 | 8.0500 | 0 | 1 | 0 | 0 | 1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 886 | 2 | 27.000000 | 0 | 0 | 13.0000 | 0 | 1 | 0 | 0 | 1 |
| 887 | 1 | 19.000000 | 0 | 0 | 30.0000 | 1 | 0 | 0 | 0 | 1 |
| 888 | 3 | 29.699118 | 1 | 2 | 23.4500 | 1 | 0 | 0 | 0 | 1 |
| 889 | 1 | 26.000000 | 0 | 0 | 30.0000 | 0 | 1 | 1 | 0 | 0 |
| 890 | 3 | 32.000000 | 0 | 0 | 7.7500 | 0 | 1 | 0 | 1 | 0 |
891 rows × 10 columns
模型搭建
(1)机器学习分为监督学习和无监督学习
(2)模型的选择可以从需求出发,也可以从样本数量和特征枢密性决定
(3)算法路径
a.分类(classification):标识对象所属类别,如图像识别
b.回归(regression):预测与对象关联的连续值属性,股票价格药物反应
c.聚类(clustering):自动将相似对象归为一组,客户细分,分组实验成果
d.降维(dimentionality reduction):减少随机变数的数量,可视化,提高效率
稍微提一嘴机器学习
大体上来看,机器学习分为四个要素:数据、任务、性能度量和模型。
这里直接引入定义:
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E.
什么意思呢,简单说就是用P(性能度量)来评估某个计算机程序在某类T(任务)中的性能,若程序在T中利用了E(经验)来提升自己的P,那么我们就说机器对经验E进行了学习。
插入一张图来简要说明四要素

数据
1.按具体类型分:结构化和非结构化
2.按表达形式分:原始和加工
3.按统计性质分:样本内外
结构化和非结构化
结构化数据
结构化数据是二维数组,它主体结构分为特征部分和标签部分。特征部分相当于多元自变量(X),标签部分相当于因变量(y),一组X和y就是一个训练样例。
非结构化数据
结构化数据的逆,图片,文字,语音等
独热编码(One-Hot Code)
一种将str或者其他非结构化的数据转为结构化数据,文字可映射成ASCII再映射为独热码,对于分类型变量,直接one-hot encoding那岂不是美滋滋
任务
1.有监督学习(有标签)
2.无监督学习(没标签)
3.半监督学习(有部分标签)
4.增强学习(有评级标签)
图片: sklearn模型算法选择路径图(集中学习下的常见任务)
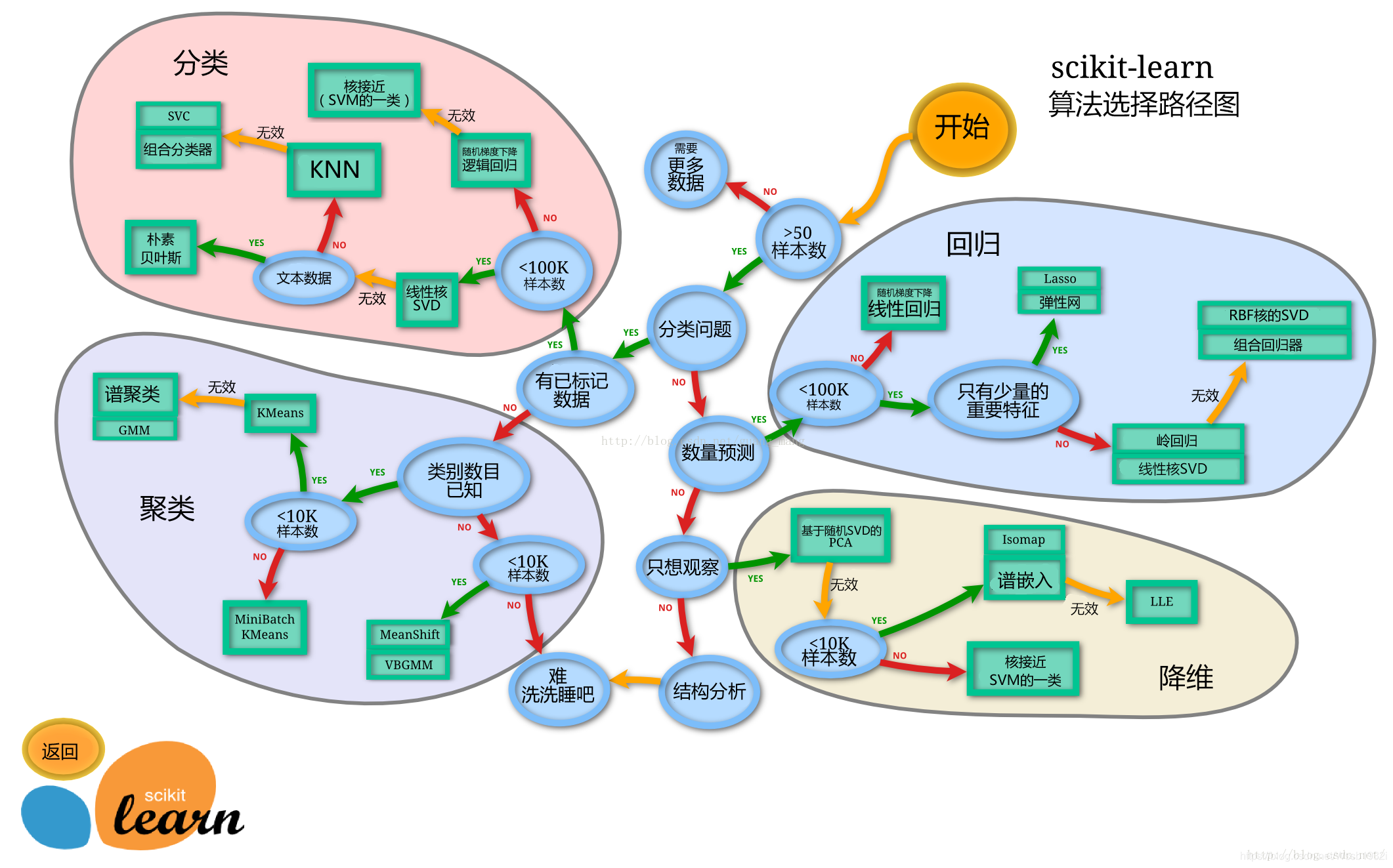
有监督学习
(1)分类:预测离散值的这类任务被称为分类。
(2)回归:预测连续值的这类任务被称为回归。
(3)聚类:对数据聚类,就是吧数据分为若干组,每组都是一簇。
(4)将为:排除对标签贡献不大的特征或数据。
1.切割训练集和测试集
·训练集和测试集:将一个数据集分为训练和测试两部分,训练部分用来训练模型,测试集用来评估模型的泛化能力
·按比例切割(测试集30%,25%,20%,15%和10%)
·按目标变量分层进行等比切割
·设置随机种子以便结果能复现
from sklearn.model_selection import train_test_split
X = data#数据集
y = train['Survived']#标签
#切割
X_train,X_test,y_train,y_test = train_test_split(X,y,stratify=y,random_state=0)
#查看数据形状
X_train.shape,X_test.shape
((668, 10), (223, 10))
模型创建
·分类模型:基于线性模型的逻辑回归LinearRegression,基于树的分类模型(决策树,随机森林)。
·线性模型所在model为sklearn.linear_model
·树模型所在model为sklearn.ensemble
#引入逻辑回顾和随机森林model
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
#默认参数逻辑回归模型
lr = LogisticRegression(max_iter = 300)
lr.fit(X_train, y_train)
LogisticRegression(max_iter=300)
print('Training set score:{:.2f}'.format(lr.score(X_train,y_train)))
print('Testing set score:{:.2f}'.format(lr.score(X_test,y_test)))
Training set score:0.80
Testing set score:0.79
#调整参数后的逻辑回归模型
lr2 = LogisticRegression(max_iter=300,C = 100)
lr2.fit(X_train,y_train)
LogisticRegression(C=100, max_iter=300)
print('Training set score:{:.2f}'.format(lr.score(X_train,y_train)))
print('Testing set score:{:.2f}'.format(lr.score(X_test,y_test)))
Training set score:0.80
Testing set score:0.79
#默认参数的随机森林分布模型
rfc = RandomForestClassifier()
rfc.fit(X_train,y_train)
RandomForestClassifier()
print("Training set score: {:.2f}".format(rfc.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(rfc.score(X_test, y_test)))
Training set score: 0.99
Testing set score: 0.81
#调整随机森林的参数
rfc2 = RandomForestClassifier(n_estimators=100, max_depth=5)
rfc2.fit(X_train, y_train)
RandomForestClassifier(max_depth=5)
print("Training set score: {:.2f}".format(rfc2.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(rfc2.score(X_test, y_test)))
Training set score: 0.86
Testing set score: 0.81
输出模型预测结果
·输出模型预测分类标签predict
·输出不同分类标签的预测概率predict_proba
#预测标签
pred = lr.predict(X_train)
pred[:10]
array([0, 1, 1, 1, 0, 0, 1, 0, 1, 1])
#预测标签概率
pred_proba = lr.predict_proba(X_train)
pred_proba[:10]
array([[0.60030085, 0.39969915],
[0.12810718, 0.87189282],
[0.46659115, 0.53340885],
[0.18637035, 0.81362965],
[0.8665119 , 0.1334881 ],
[0.91112557, 0.08887443],
[0.12006672, 0.87993328],
[0.90988944, 0.09011056],
[0.04883764, 0.95116236],
[0.13186542, 0.86813458]])
模型建立和评估-评估
交叉验证
·模型评估评估的是模型的泛化能力。
·交叉验证(cross-validation)是一种评估泛化性能的统计学方法,它比单次划分训练集和测试集的方法更稳定、全面。
·k-fold cross-validation

k折交叉验证,k一般取5-10,将一个数据集重复进行k次不同的划分(划分为k对不同的train和test集),进行k次测验,将成绩取平均值。
·准确率(precision)度量的是被预测为正例的样本中有多少是真正的正例。
·召回率(recall)度量的是正类样本中有多少被预测为正类
·f-分数是准确率与召回率的调和平均
·交叉验证在sklearn中的model为sklearn.model_selection
from sklearn.model_selection import cross_val_score
lr = LogisticRegression(max_iter = 300,C=100)
scores = cross_val_score(lr,X_train,y_train,cv=10)
scores
array([0.8358209 , 0.7761194 , 0.82089552, 0.79104478, 0.85074627,
0.86567164, 0.73134328, 0.86567164, 0.75757576, 0.71212121])
# 平均交叉验证分数
print("Average cross-validation score: {:.2f}".format(scores.mean()))
Average cross-validation score: 0.80
混淆矩阵(Confusion Matrix)
混淆矩阵是一种可视化模型预测结果和世界结果对照的工具
主对角线上的元素就是预测正确的元素
这里主要介绍二分类的混淆矩阵

【注释】:
TN(True Negative):真负类
FP(False Positive):假正类
FN(False Negative):假负类
TP(True Positive):真正类
Positive和Negative都指的是预测结果的分类,而不是真实情况的分类,True和False指的是预测结果的正确与否
很自然的引入一些根据Confusion Matrix可以得到的结论
(1)Accuracy:
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN?
(2)Precision:
P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP+FP} Precision=TP+FPTP?
(3)Recall(True Positive Rate)(Sensitivity):
T P R or R e c a l l = T P T P + F N TPR \quad \text{or} \quad Recall = \frac{TP}{TP+FN} TPRorRecall=TP+FNTP?
(4)Specificity(False Positive Rate):
F P R or S p e c i f i c i t y = F P F P + T N FPR\quad \text{or}\quad Specificity = \frac{FP}{FP+TN} FPRorSpecificity=FP+TNFP?
(5)Fβ_Score:
Fβ的物理意义就是将正确率和召回率的一种加权平均(应该是加权调和平均),在合并的过程中,召回率的权重(权数)是正确率的β倍。
对于二分类问题,一般用F1_Score,F1_Score取值是0到1,越高越好。但是为什么用F1_score呢?
一般来讲,Accuracy和F1_Score是判断分类模型总体的标准。
F1?Score = 2 ( P r e s i c i o n × T P R P r e c i s i o n + T P R ) \text{F1 Score} = 2(\frac{Presicion \times TPR}{Precision+TPR}) F1?Score=2(Precision+TPRPresicion×TPR?)
混淆矩阵的方法在sklearn.metrics模块
混淆矩阵需要输入真实标签和预测标签
#其他可以从confusion matrix里得到的相关参数(from wikipedia)
Image('Annotation 2021-07-21 153910.jpg')

from sklearn.metrics import confusion_matrix
confusion_matrix(y_train,pred)
array([[353, 59],
[ 72, 184]])
#classification_report方法得到Precision等参数
from sklearn.metrics import classification_report
print(classification_report(y_train,pred))
precision recall f1-score support
0 0.83 0.86 0.84 412
1 0.76 0.72 0.74 256
accuracy 0.80 668
macro avg 0.79 0.79 0.79 668
weighted avg 0.80 0.80 0.80 668
实际上,FPR和TPR才是更具有参考意义的,具象点来说,就是可以看出实际positive的样本里模型识别出来多少,实际negative的样本里模型认错了多少。Accuracy在不平衡样本中的参考意义其实并不如这两项。
ROC(Receiver Operating characteristic Curve)/AUC(Area Under the Curve of ROC)
通过对confusion matrix的理解,我们发现FPR和TPR可以很好的衡量一个模型的泛化能力,那么我们可以试着通过这两个参数,将模型的泛化能力可视化。
如果我们将FPR和TPR分别作为横纵坐标,我们可以得到一个点,这个点是(FPR,TPR)。
显然,我们希望TPR尽可能大,FPR尽可能小,所以反映在坐标系上,这个点越靠近左上角越符合我们的期望。
但是光有一个点是不够的,我们可以将不同参数设定下的分类器的表现汇集到一张图中,这样就可以看出哪个参数是最好的(最适合的)。
而这个参数就是判定为T的阈值,对一个数据,分类器会给出这个数据为T的概率,并定义一个概率,超过这个概率就判定为T,低于这个概率就判定为F。
此时,我们可以依次定义阈值为每一个数据为T的这个概率,这样我们就得到了很多点,这些点连起来就是ROC曲线。
这里可以解释一下ROC的命名(个人见解)Receiver Operating characteristic Curve,接收者操作特征曲线,可以理解为是同一组数据,给同一个Receiver,得到了不同的Character,原因就在于你的Operating标准不同,也就是你设定的阈值不同。把这些所有数据汇聚到一起,就成了一个Curve
对于AUC,这里我的理解非常浅显,从上面我们对ROC曲线理解可知,当ROC整体高于y=x时,ROC曲线越接近y=x,你的模型越接近“随机分类”,TF的概率各50%(基本上就是没用),当你的ROC大部分低于y=x时,恭喜你,请马上去买彩票。
那么曲线整体相对y=x的高低,可以用面积来表示,
AUC
?
图
表
总
面
积
2
\text{AUC}-\frac{图表总面积}{2}
AUC?2图表总面积?的取值正负,意味着总体相对高低,由于这个值和AUC是线性关系(美妙至极),我们就可以粗略认为AUC高的模型就是好模型。
【个人注】:我依旧没有搞明白,靠近左上角是什么意思,如果两个点距离左上角的距离相同,如何斟酌,此时设定TPR和FPR的权重就显得尤为重要,不过我没有找到相关资料,也许是因为二分类分类器模型处理的问题都比较简单,这种刁钻问题有更好的模型吧。
#这里直接引入sklearn.metrix里的roc_curve
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score
#lr.fit(X_test,y_test)#妈的老子改了好久,这里下次注意,报错是说没有fit decision_function里面的arguments,fit完以后这行代码又没用了,留个纪念吧
fpr, tpr, thresholds = roc_curve(y_test,lr.decision_function(X_test))
plt.plot(fpr, tpr, label="ROC Curve LR")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
# 找到最接近于0的阈值
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10, label="threshold zero")
#再画一张RFC的ROC图
fpr2,tpr2,thresholds2 = roc_curve(y_test,rfc.predict_proba(X_test)[:,1])
plt.plot(fpr2,tpr2,label="ROC Curve RFC")
plt.plot(fpr2[close_zero],tpr2[close_zero],'s',markersize=10,label="threshold zero2")
#加上图例
plt.legend(loc=4)
<matplotlib.legend.Legend at 0x7fd74800ef40>

a = roc_auc_score(y_test, lr.decision_function(X_test))
print('AUC of LR is: '"%.2f" % a)
b = roc_auc_score(y_test, rfc.predict_proba(X_test)[:,1])
print('AUC of RFC is: '"%.2f" % b)
AUC of LR is: 0.84
AUC of RFC is: 0.84
那么ROC/AUC为什么好?
ROC是根据FPR和TPR画出来的,而这两个参数不会收到数据分布不均(T数据明显多于F数据或反之)影响,这保证了模型面对不同的数据集时图像稳定,也就是图像反映出的模型特性也更稳定,能更好的反映出来模型的问题在哪。
至于AUC的计算公式(一个简单的积分,简单到
Δ
x
\Delta x
Δx不用很小就足够精确,因为全是规则矩形对吧)这里也不多赘述,网上能看到很多深入浅出的解释。