一、Q表格
我们可以用状态动作价值来表达说在某个状态下,为什么动作 1 会比动作 2 好,因为动作 1 的价值比动作 2 要高,这个价值就叫 Q 函数。
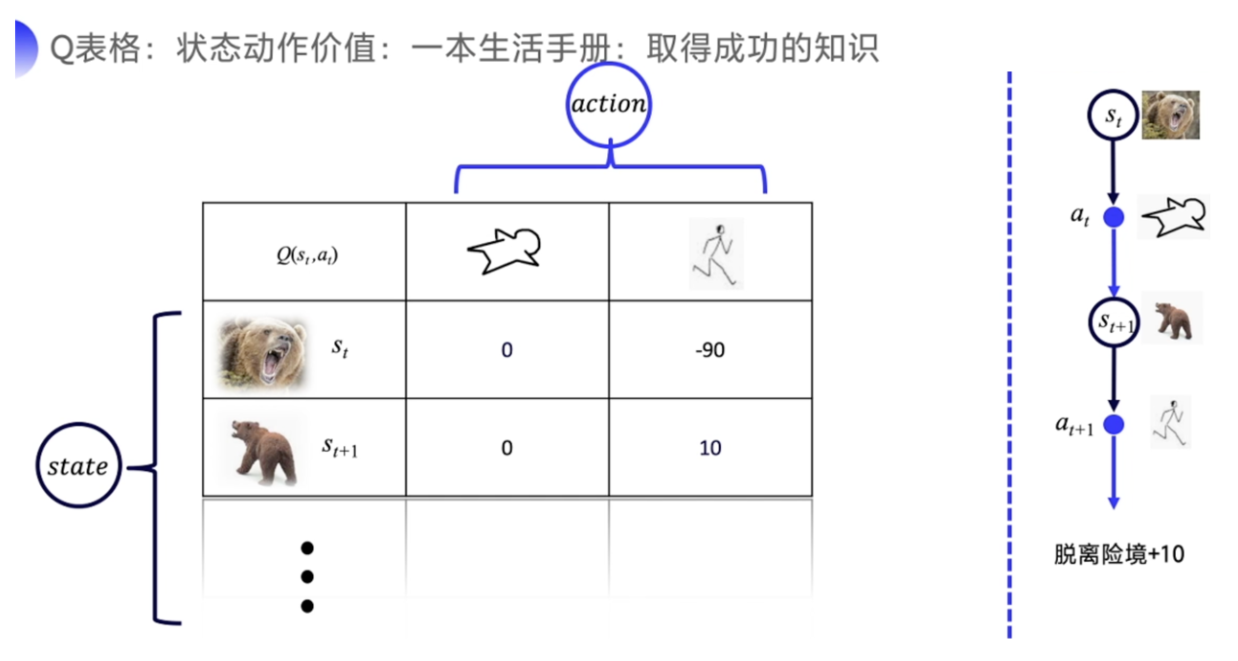
如果 Q 表格是一张已经训练好的表格的话,那这一张表格就像是一本生活手册。 我们就知道在熊发怒的时候,装死的价值会高一点。在熊离开的时候,我们可能偷偷逃跑的会比较容易获救。
这张表格里面 Q 函数的意义就是我选择了这个动作之后,最后面能不能成功,就是我需要去计算在这个状态下,我选择了这个动作,后续能够一共拿到多少总收益。如果可以预估未来的总收益的大小,我们当然知道在当前的这个状态下选择哪个动作,价值更高。我选择某个动作是因为我未来可以拿到的那个价值会更高一点。所以强化学习的目标导向性很强,环境给出的奖励是一个非常重要的反馈,它就是根据环境的奖励来去做选择。
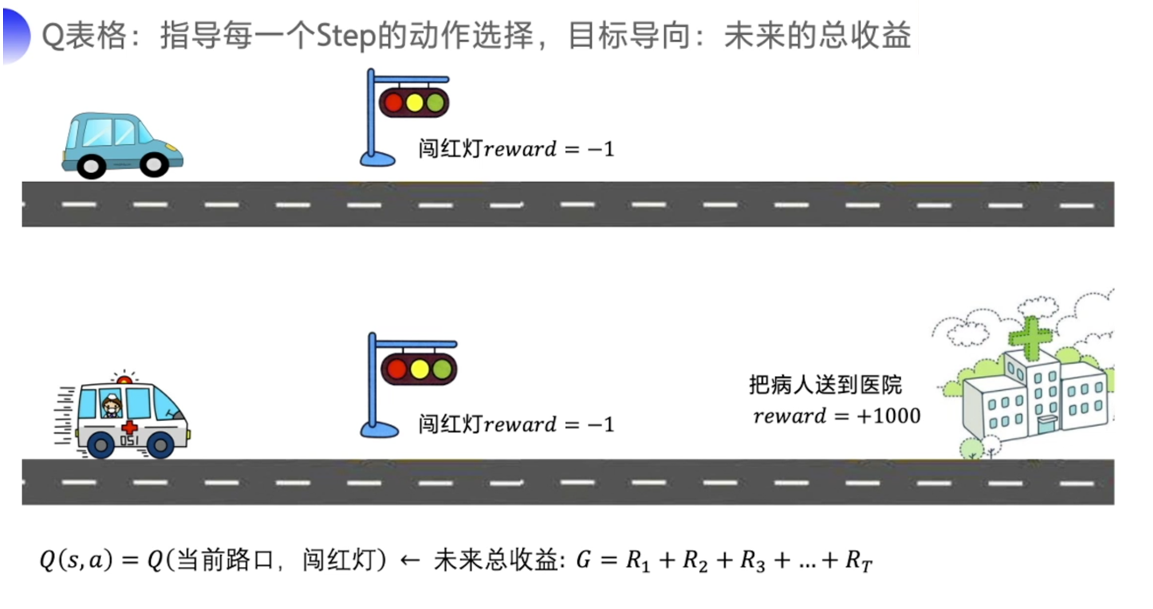
为什么可以用未来的总收益来评价当前这个动作是好是坏?
A: 举个例子,假设一辆车在路上,当前是红灯,我们直接走的收益就很低,因为违反交通规则,这就是当前的单步收益。可是如果我们这是一辆救护车,我们正在运送病人,把病人快速送达医院的收益非常的高,而且越快你的收益越大。在这种情况下,我们很可能应该要闯红灯,因为未来的远期收益太高了。这也是为什么强化学习需要去学习远期的收益,因为在现实世界中奖励往往是延迟的。所以我们一般会从当前状态开始,把后续有可能会收到所有收益加起来计算当前动作的 Q 的价值,让 Q 的价值可以真正地代表当前这个状态下,动作的真正的价值。
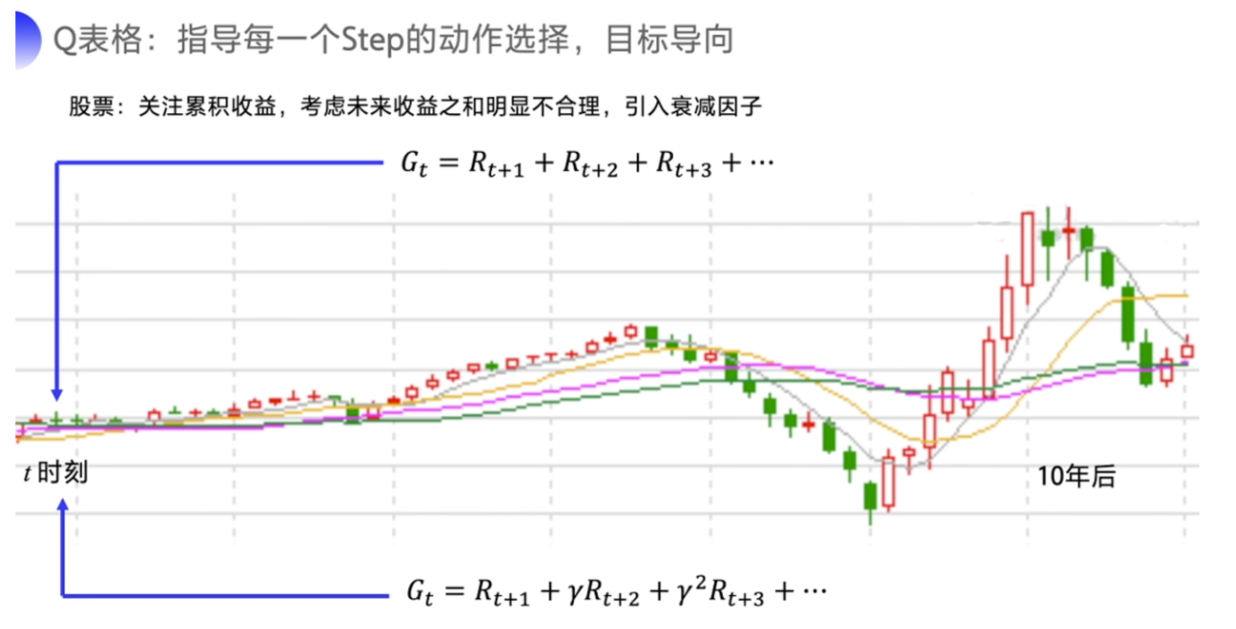
但有的时候把目光放得太长远不好,因为如果事情很快就结束的话,你考虑到最后一步的收益无可厚非。如果是一个持续的没有尽头的任务,即持续式任务(Continuing Task),你把未来的收益全部相加,作为当前的状态价值就很不合理。
股票的例子就很典型了,我们要关注的是累积的收益。可是如果说十年之后才有一次大涨大跌,你显然不会把十年后的收益也作为当前动作的考虑因素。那我们会怎么办呢,有句俗话说得好,对远一点的东西,我们就当做近视,就不需要看得太清楚,我们可以引入这个衰减因子γ 来去计算这个未来总收益,γ∈[0,1],越往后 γ^n就会越小,也就是说越后面的收益对当前价值的影响就会越小。
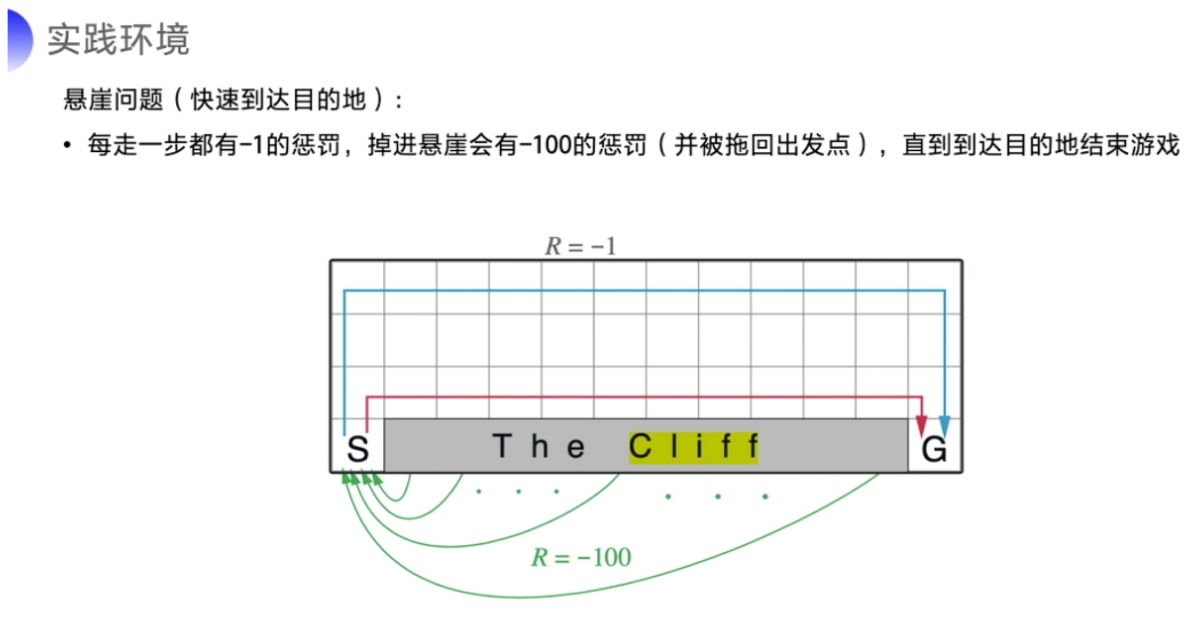
举个例子来看看计算出来的是什么效果。这是一个悬崖问题,这个问题是需要智能体从出发点 S 出发,到达目的地 G,同时避免掉进悬崖(cliff),掉进悬崖的话就会有 -100 分的惩罚,但游戏不会结束,它会被直接拖回起点,游戏继续。为了到达目的地,我们可以沿着蓝线和红线走。
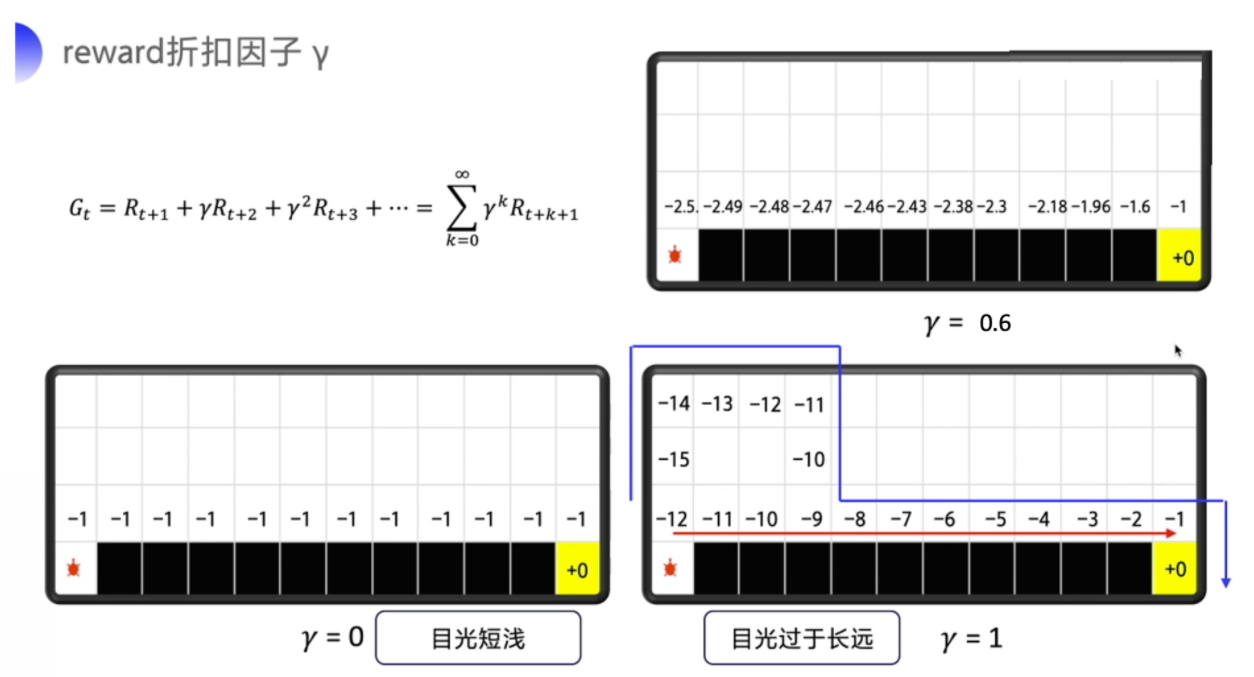

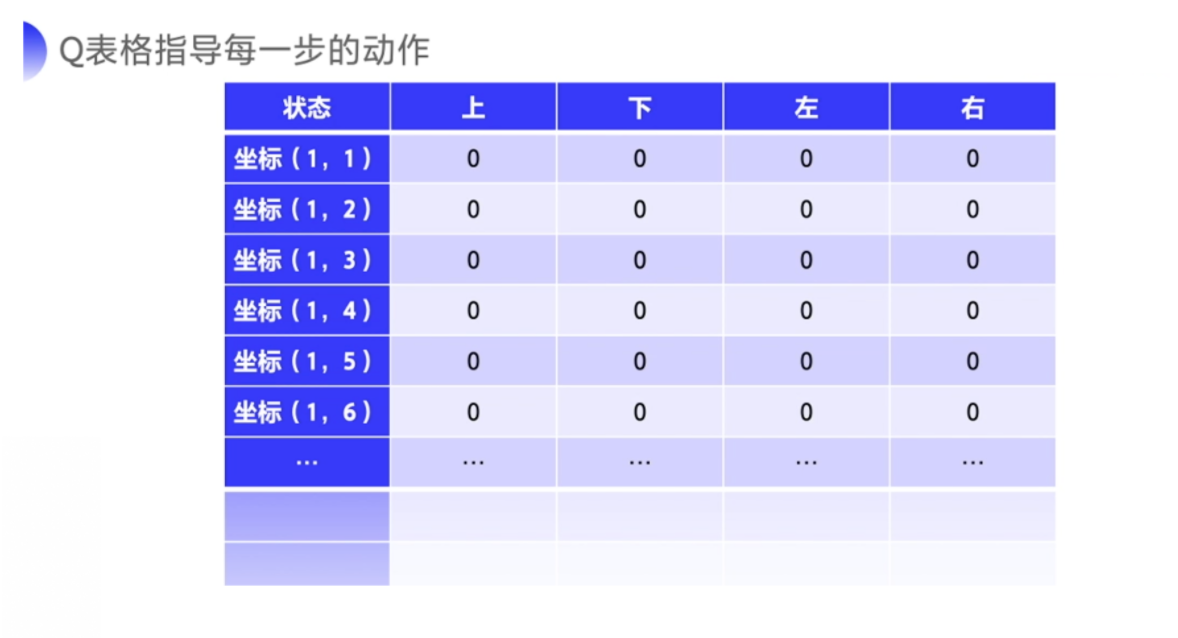
类似于上图,最后我们要求解的就是一张 Q 表格,
- 它的行数是所有的状态数量,一般可以用坐标来表示表示格子的状态,也可以用 1、2、3、4、5、6、7 来表示不同的位置。
- Q 表格的列表示上下左右四个动作。
最开始这张 Q 表格会全部初始化为零,然后 agent 会不断地去和环境交互得到不同的轨迹,当交互的次数足够多的时候,我们就可以估算出每一个状态下,每个行动的平均总收益去更新这个 Q 表格。怎么去更新 Q 表格就是接下来要引入的强化概念。
强化就是我们可以用下一个状态的价值来更新当前状态的价值,其实就是强化学习里面 bootstrapping 的概念。在强化学习里面,你可以每走一步更新一下 Q 表格,然后用下一个状态的 Q 值来更新这个状态的 Q 值,这种单步更新的方法叫做时序差分。








二、时间差分法(Temporal-Difference)
时间差分法的思路与蒙特卡罗法不同,它不希望机器人通过一个完整的 Episode 试探之后才对一个状态进行估算,它可以走一步就估算一次。
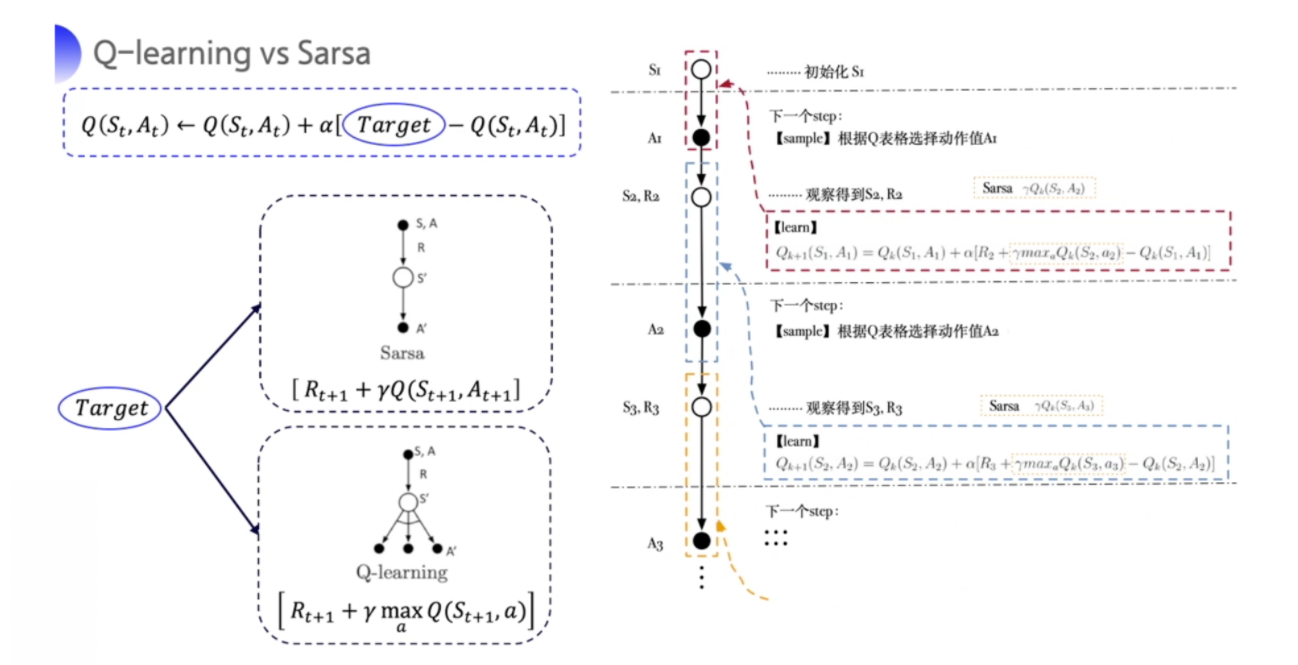
三、Sarsa算法
从结构上来看,Sarsa算法是 𝑆 → 𝐴 → 𝑅 → 𝑆 →𝐴 的缩写。在状态S下。要想把动作𝐴的估值 𝑄(𝑆, 𝐴) 计算准确,需要研究这个序列:𝑆 → 𝐴 → 𝑅 → 𝑆′ → 𝐴′,并对这个序列中的估值进行调整,从而使得方程收敛。
更新方程为:
- 𝑄(𝑆, 𝐴) ← 𝑄(𝑆, 𝐴) + 𝛼(𝑅𝑅 + 𝛾𝑄(𝑆′, 𝐴′) ? 𝑄(𝑆, 𝐴))
解释:SARSA 算法的表现形式是 𝑄(𝑆, 𝐴),即对某个状态下的一个动作做估值计算。在状态 𝑆 下,做一个动作 𝐴,它的估值 𝑄(𝑆, 𝐴) 需要的迭代计算逻辑是当前的 𝑄(𝑆, 𝐴)与一个 𝛼 倍的叠加值相加。
对于𝛼,可以认为 𝛼 值越小,说明“记忆”周期越长,也可以认为对于估值,“平均”的周期越长。
这个叠加值,是用瞬时回报 𝑅 和 𝛾 倍的下一个状态下的动作估值 𝑄(𝑆′, 𝐴′) 相减得到的。
𝛾 是折扣系数,表示对于长期回报的好坏。𝛾 的值值在 0 和 1 之间:值越大,说明算法越“远视”,即对远期的回报越重视,越倾向于把它们的得失算在当前决策的头上;值越小,说明算法越“无视”长期回报。
𝛼 的值越小,则估值变化越慢、越平滑,也就越能参考更长周期的变化平均值;𝛼 的
值越大,则变化越快、越剧烈,也就越关注最近几个时间周期的变化平均值。时间差分法走一步(一个 Step 循环)就进行一次更新,不必等到整个 Episode 结束再进行更新。𝛼 取得小一些,让变化的平滑度高一些。
Sarsa算法伪代码

??首先,函数 𝑄(𝑠, 𝑎) 的初始化其实是一个随机性比较强的过程,其原因还是在于冷启动时没有参考数据。因此,不妨设置一个空列表,这样在查表的时候会得到任意一个状态的任意动作的估值 𝑄(𝑠, 𝑎) = 0。这个问题在实际应用中影响不大,反正最开始估值的准确性不是那么重要。终止状态必须是 𝑄(𝑠, 𝑎) = 0
??接下来,让机器人在环境中不停地“玩游戏”(如图所示)——从“诞生”时就开始玩,直到出现 Terminal 的状态,也就是伪代码中所述的终止状态。这就是一个完整的 Episode 过程.

??对每个 Episode 来说,都要初始化一个状态 𝑠,让机器人开始学习(这可以通过 𝑄(𝑠, 𝑎) 和 ε-greedy 方法实现)。ε-greedy 方法的要点如下:
- 令 ε 取一个 0 和 1 之间的数字——概率。
- 以 1 ? ε 的概率,让机器人做 𝑎? = argmax𝑄(𝑠,𝑎) (𝑎∈𝐴)的动作,也就是 𝑄(𝑠,𝑎) 中能够产生最高估值的动作𝑎
- 以 ε 的概率进行试探,随机做一个动作,以兼顾试探和最优动作选择的方式不断提高机器人输出动作的质量。
??SARSA 算法是一种 On-Policy(在线)算法,也是基于一种已有策略的估算,如图所示。因此,在进化的过程中,机器人能知道 𝑆 → 𝐴 → 𝑅 → 𝑆′ → 𝐴′ 这个确定的序列的样子,并能根它把估值计算准确。
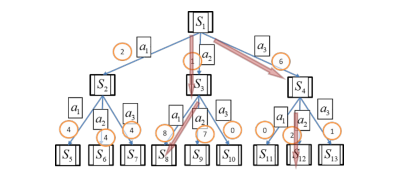
??在图中,𝑆1 到 𝑆13 只表示不同的状态,不表示严格意义上的次序。如果想要估算在 𝑆1 状态下做动作 𝑎1 、𝑎2 、𝑎3 的估值,除了要把过去学到的 𝑄(𝑆,𝐴) 保留下来,还要参考根据当前策略所到达的状态及在这个状态下动作的估值 𝑄(𝑆′,𝐴′),也就是
- 𝑄(𝑆,𝐴) ← 𝑄(𝑆,𝐴) + 𝛼(𝑅 + 𝛾𝑄(𝑆′,𝐴′) ? 𝑄(𝑆,𝐴))
??至于 𝑄(𝑆′,𝐴′) 的估值,仍旧通过在一次一次的 Episode 中学习得到。
简言之,SARSA 评估的内容是在一个策略下的 𝑄(𝑆,𝐴),方法是:评估当前状态的 𝑄(𝑆,𝐴),要参考当前策略下的下一个状态的 𝑄(𝑆′,𝐴′),通过这种将 𝑄 的值(奖励值)层层回溯的方式,逐步调整状态 𝑄(𝑆,𝐴) 的估值。
四、Q-Learning算法
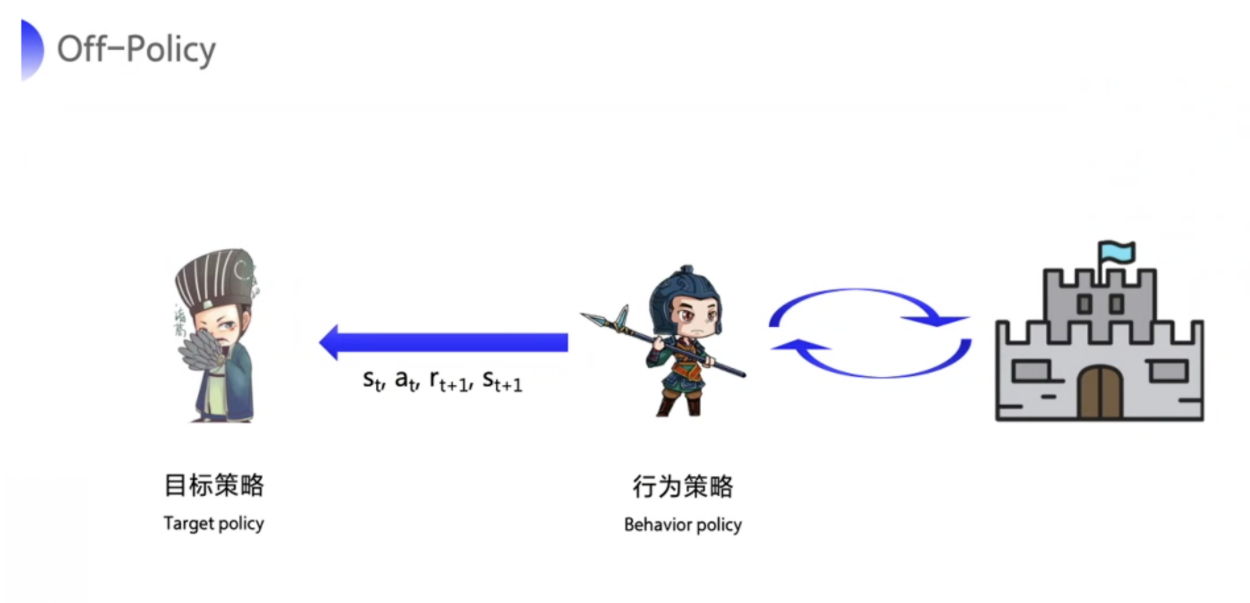
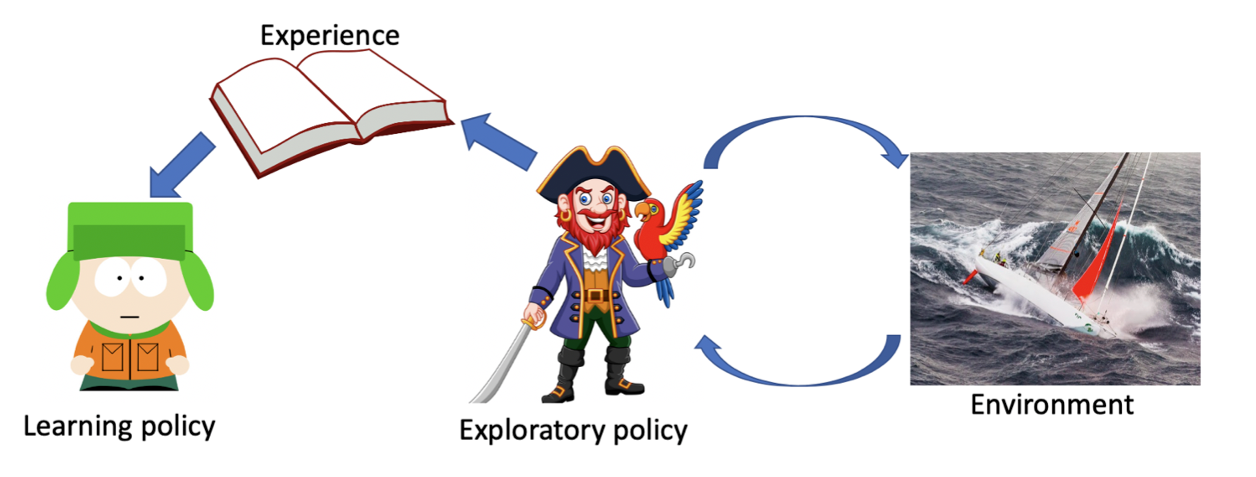
??Q-Learning 算法是强化学习中最为有效、最具普适性的算法。尽管从名字上看不出它是如何工作的,但它仍然是一个 TD 算法,并且是 Off-Policy(离线)的——这一点与 SARSA不同,SARSA 是 On-Policy 的。请看公式:
- Q-Learning 算法:𝑄(𝑆,𝐴) ← 𝑄(𝑆,𝐴) + 𝛼(𝑅 + 𝛾max𝑎′𝑄(𝑆′,𝐴′) ? 𝑄(𝑆,𝐴))。
- SARSA 算法:𝑄(𝑆,𝐴) ← 𝑄(𝑆,𝐴) + 𝛼(𝑅 + 𝛾𝑄(𝑆′,𝐴′) ? 𝑄(𝑆,𝐴))。
??从形式上看,只有后半部分不同。SARSA 算法使用的是一个带有折扣的估值 𝛾𝑄(𝑆𝑆′,𝐴𝐴′),而Q-Learning 算法使用的是一个带有折扣的 𝛾max𝑎′𝑄(𝑆′,𝐴′),差别就在“max”上。
??Q-Learning 算法对 𝑄(𝑆,𝐴) 的估值,同样参考了其后所能转移到的所有状态 𝑆′ 可能做的所有动作 𝑎′,并认为其中的最大估值才是当前 𝑄(𝑆,𝐴) 的估值。这个思路是非常明确的:当前状态𝑄(𝑆,𝐴) 的大小,取决于在它转移到的状态下,哪个 𝑎′ 能够取得最大的估值(奖励值)及估值为多少。
??用一句话概括:既然曾经有人在这么做之后能够达到某个估值,那么策略就应该将这个动作作为输出,以谋求“利益最大化”。
Q-Learning算法伪代码

这段伪代码和 SARSA 算法的伪代码非常像,主要的差别在对估值函数进行更新的表达式上。相信有 SARSA 算法做铺垫,对 Q-Learning 算法的功能,我们能通过伪代码了解得差不多:

??在 𝑄(𝑆,𝐴) 的估值中,除了当前的直接奖励值 𝑅,还有 max𝑎 ′𝑄(𝑆 ′ ,𝑎 ′ )。在这里没有强调 𝑆 ′和 𝑎 是在同一个策略下产生的,相反,我们其实更希望这是不同策略下的 𝑆′ 和 𝑎 的行为估值。因为只有这样,才会有比较丰富的 𝑄(𝑆′,𝑎),在其中挑选“max”的时候,才能够发现比较好的 𝑆和 𝑎 的值,从而把其时间序列前方的 𝑄(𝑆,𝐴) 估算得更“准确”,或者说,更容易发现比较好的策略行为路径,进而得到比较好的策略。
参考
- 百度强化学习
- 强化学习纲要
- 白话强化学习