一.插值算法的用途
- 在数模比赛中,需要用已知数据进行分析时,可能会出现已知数据缺失/不足的情况,此时可利用该方法产生一些靠谱的数据点。
- 数据量太小,需要增加数据量来提升算法的执行效果。比如机器学习、深度学习中的样本如果太少,可以用插值法得到更多的样本值。
- 需要对某个区域的值进行预测。通过插值算法将插值点的值计算出来。
二.什么是插值算法?
插值算法的重点在于找出插值函数----包含了所有已知数据点的函数

?三.插法分类
- 内插法-只对已知数据点集内部的点进行的插值运算称为内插,可比较准确的估测插值点上的函数值。
- 外插法-当插值点落在已知数据集的外部时的插值称为外插,要估计外插函数值很难。
四.建模比赛常用的插值方法---分段插值
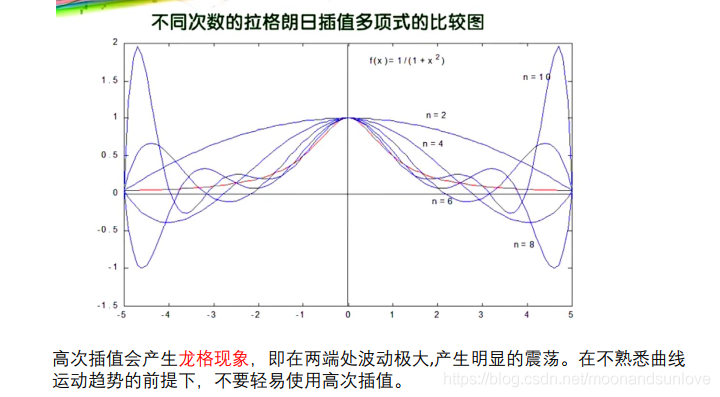
拉格朗日插值、牛顿插值、hermite插值 都会存在龙格现象的问题,所以采用分段插值来避免这种现象。
龙格现象 :在计算方法中,有利用多项式对某一函数的近似逼近,计算相应的函数值。. 一般情况下,多项式的次数越多,需要的数据就越多,而预测也就越准确。. 插值次数越高,插值结果越偏离原函数的现象称为龙格现象。.
?看上面的不同次数下图像的比较图可以方便理解龙格现象,如图:n=10次时,曲线两端的波动极大,并且n越大,这种现象越明显。我们应该尽量避免该现象的发生
分段插值分为:分段三次埃尔米特插值和三次样条插值。 一般的建模比赛都可以用这2种方法求解
1.分段三次埃尔米特插值【MATLAB对应函数:p = pchip(x,y, new_x)】
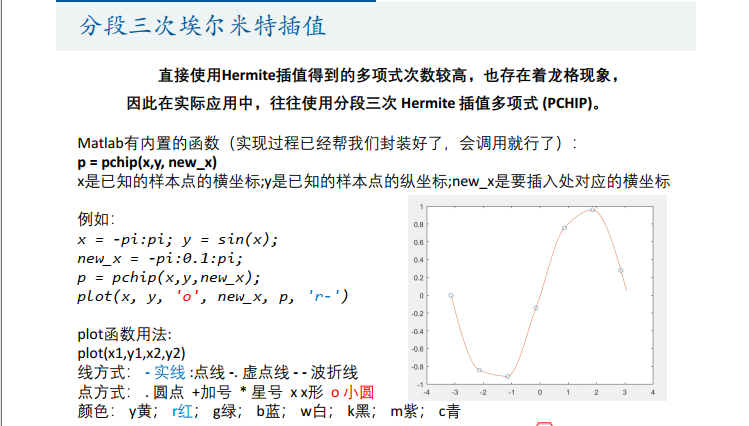
用法很简单,在MATLAB中有封装好的函数,直接调用即可,函数为:pchip(x,y,new_x)
上图中有具体说明。
 ?
?
?2.三次样条插值【MATLAB对应函数: p = spline (x,y, new_x)】


?五.总结
- 插值算法实现起来较简单,只需要调用对应的函数即可
- 不同插值算法都可以求出包含了所有已知数据点的插值函数,只是在满足这个基本要求的基础上,对插值函数有不同的约束条件。