[人工智能]LBP算子总结（人脸检测）

LBP算法介绍

1LBP算子

LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietik?inen,和 D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征。

1.1原始的LBP算子

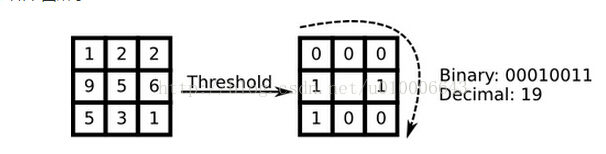
原始的LBP算子定义为在3*3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示：

但是随着算法的发展，大家发现这个算子不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala等对 LBP 算子进行了改进，将 3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域。

1.2 圆形LBP算子

基本的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala等对 LBP算子进行了改进，将 3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的 LBP算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子。每个采样点坐标为：
$$\begin{gathered} x_p=x_c+Rcos(\frac{2\pi k}{p}) \\ {y}_p=y_c+Rsin(\frac{2\pi k}{p}) \\ k=0,1,...,p?1 \end{gathered}$$
此时得到的不一定是整数，可以通过双线性插值来取整，此不再详述。

2 LBP旋转不变模式

从 LBP 的定义可以看出，LBP 算子是灰度不变的，但却不是旋转不变的。图像的旋转就会得到不同的 LBP值。
Maenpaa等人又将 LBP算子进行了扩展，提出了具有旋转不变性的 LBP算子，即不断旋转圆形邻域得到一系列初始定义的 LBP值，取其最小值作为该邻域的 LBP值。
图 2.5 给出了求取旋转不变的 LBP 的过程示意图，图中算子下方的数字表示该算子对应的 LBP值，图中所示的 8种 LBP模式，经过旋转不变的处理，最终得到的具有旋转不变性的 LBP值为 15。也就是说，图中的 8种 LBP 模式对应的旋转不变的 LBP模式都是 00001111。

3 LBP等价模式

一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生$2^p$种模式。(P个邻域点，每个邻域点和中心像素比较结果只能是0或者1，就相当于每次比较会有0和1两种选择，P次比较就是$2^P$）。
很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。例如：5×5邻域内20个采样点，有$2^{20}$＝1,048,576种二进制模式。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。同时，过多的模式种类对于纹理的表达是不利的。例如，将LBP算子用于纹理分类或人脸识别时，常采用LBP模式的统计直方图来表达图像的信息，而较多的模式种类将使得数据量过大，且直方图过于稀疏。因此，需要对原始的LBP模式进行降维，使得数据量减少的情况下能最好的代表图像的信息。
为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”（Uniform Pattern）来对LBP算子的模式种类进行降维。Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000（0次跳变），00000111（只含一次从0到1的跳变），10001111（先由1跳到0，再由0跳到1，共两次跳变）都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111（共四次跳变）。
以LBP（1,8）为例，即在半径为1的环形区域上8个采样点的领域进行LBP编码，原始的二进制模式为28=256种，等价模式为P*（P-1）+2=58种，那为什么就是58种二进制模式？
首先，要注意Ojala对等价模式的定义，即当某个局部二进制模式所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该局部二进制模式所对应的二进制就成为一个等价模式类；
其次，对于式子P*（P-1）+2中的2，很容易理解，其模式即为0000 0000和1111 1111，这是0到1或1到0跳变次数为0的情况；
最后，式子中的P*（P-1）怎么理解？稍微列举一些等价模式就能发现规律，如1011 1111，1001 1111，1000 1111，0001 1111等，可以发现，这些等价模式中0到1或1到0的跳变次数为2（注意：等价模式中不存在跳变次数为1的情况），而且其中0的出现必须是连续的（观察以0的出现规律为例，1的出现规律类似），0连续出现的意思是中间不出现1。
利用一种直观的较笨的方法进行统计如下：
当8个二进制位中只出现1个0时，0的位置存在8种情况，即0111 1111,1011 1111,1101 1111,1110 1111,1111 0111,1111 1011,1111 1101,1111 1110。
当8个二进制位中连续出现两个0时，00的位置也存在8种情况，即0011 1111,1001 1111,1100 1111,1110 0111，1111 0011,1111 1001,1111 1100，0111 1110。
…
当8个二进制位中连续出现7个0时，0000 000的位置也存在8种情况。
这样，规律就出现了，总共有8*（8-1）=56种情况。
综上：如果对像素进行LBP（R，P）编码时，采用等价模式，产生的二进制模式种类为P*（P-1）+2种。

4 LBP特征用于检测的原理

显而易见的是，上述提取的LBP算子在每个像素点都可以得到一个LBP“编码”，那么，对一幅图像（记录的是每个像素点的灰度值）提取其原始的LBP算子之后，得到的原始LBP特征依然是“一幅图片”（记录的是每个像素点的LBP值）。
LBP的应用中，如纹理分类、人脸分析等，一般都不将LBP图谱作为特征向量用于分类识别，而是采用LBP特征谱的统计直方图作为特征向量用于分类识别。因为，从上面的分析我们可以看出，这个“特征”跟位置信息是紧密相关的。直接对两幅图片提取这种“特征”，并进行判别分析的话，会因为“位置没有对准”而产生很大的误差。后来，研究人员发现，可以将一幅图片划分为若干的子区域，对每个子区域内的每个像素点都提取LBP特征，然后，在每个子区域内建立LBP特征的统计直方图。如此一来，每个子区域，就可以用一个统计直方图来进行描述；整个图片就由若干个统计直方图组成；
例如：一幅100*100像素大小的图片，划分为10*10=100个子区域（可以通过多种方式来划分区域），每个子区域的大小为10*10像素；在每个子区域内的每个像素点，提取其LBP特征，然后，建立统计直方图；这样，这幅图片就有10*10个子区域，也就有了10*10个统计直方图，利用这10*10个统计直方图，就可以描述这幅图片了。之后，我们利用各种相似性度量函数，就可以判断两幅图像之间的相似性了；

对LBP特征向量进行提取的步骤如下：

（1）首先将检测窗口划分为16×16的小区域（cell）；

（2）对于每个cell中的一个像素，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3*3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值；

（3）然后计算每个cell的直方图，即每个数字（假定是十进制数LBP值）出现的频率；然后对该直方图进行归一化处理。

（4）最后将得到的每个cell的统计直方图进行连接成为一个特征向量，也就是整幅图的LBP纹理特征向量；

然后便可利用SVM或者其他机器学习算法进行分类了。

————————————————

参考链接

https://ac.csdn.net/?spm=1001.2101.3001.5716
https://blog.csdn.net/u010006643/article/details/46417091
https://blog.csdn.net/sad_123_happy/article/details/9087989