Architecture

Inception module

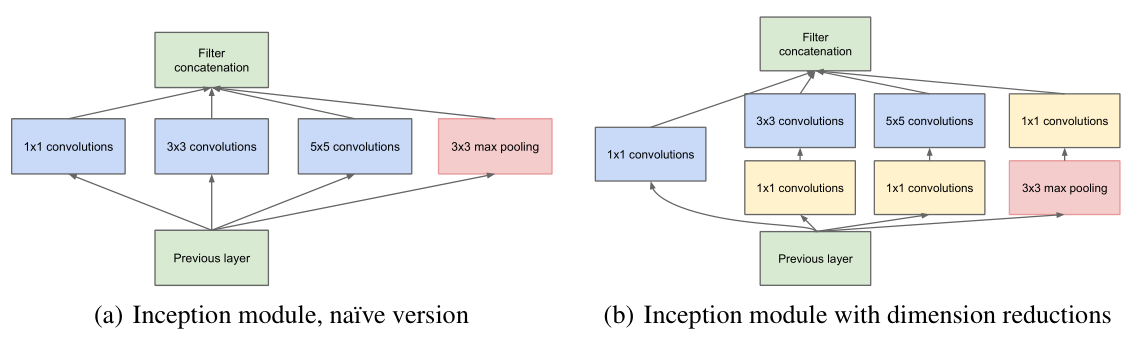
在这里插入图片描述

parallel conv. with different kernel size
visual information should be processed at various scales and then aggregated
→the next stage can abstract features from different scales simultaneously
max pooling
pooling operations have been essential for the success in current state of the art convolutional networks
1×1 conv.
① dimension reduction→remove computational bottlenecks
② increase the representational power
refer to Network-in-Network

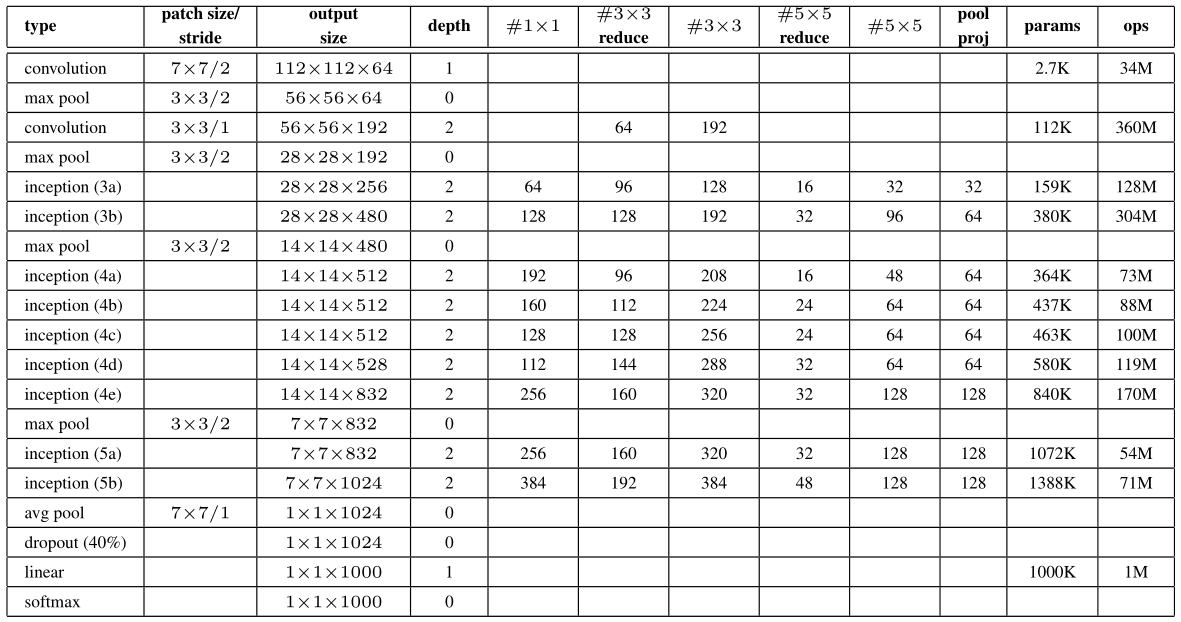
GoogLeNet

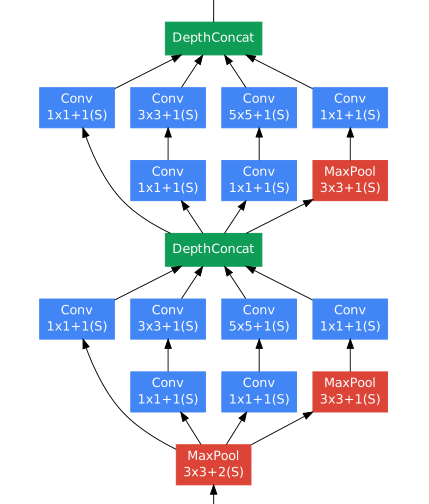
在这里插入图片描述
i.e. inception(3a)+(3b):

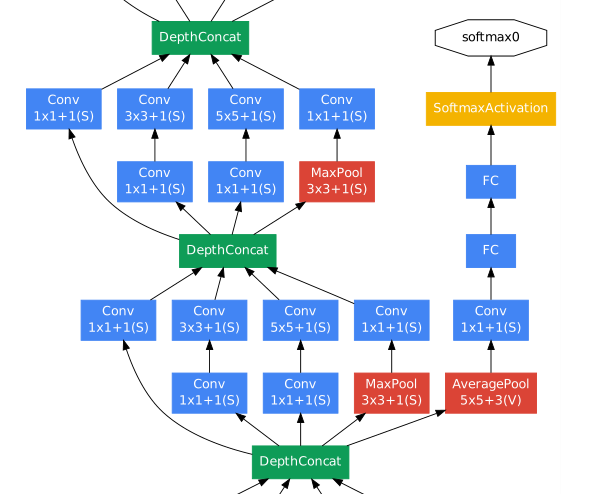
all conv. use ReLU
input→224×224 taking RGB channels with mean subtraction
#3×3 reduce→1×1filters in the reduction layer used before the 3×3 conv.
linear→FC
add auxiliary classifiers connected to intermediate layers
→encourage discrimination in lower stages in the classifier, increase the gradient signal that gets propagated back, provide additional regularization
put on top of output of the Inception(4a) and (4d) modules
during training, their loss gets added to the total loss of the network with a sidcount weight(0.3)
the structure:
在这里插入图片描述

Training

asynchronous stochastic gradient descent with 0.9 momentum, fixed learning rate schedule(decreasing the learning rate by 4% every 8 epochs)
image sampling method work well
sampling of various sized patches of the image whose size is distributed evenly between 8% and 100% of the image area and whose aspect radio is chosen randomly between 3/4 and 4/3

testing

resize the image to 4 scales where the shorter dimense is 256, 288, 320 and 352 respectively
take the left, center and right square of resized images (portrait-top, center and bottom)
for each square, take the 4 corners and center 224×224 crop +square resized to 224×224+mirrored version
→4×3×6×2=144 crops per image
note: such aggressive cropping may not be necessary in real application

Appendix

Network In Network

convolution filter in CNN is a generalized linear model(GLM) for the underlying data patch
replace the GLM with more potent nonlinear function approximator (in this paper, multilayer perceptron) can enhance the abstraction ability of the local model
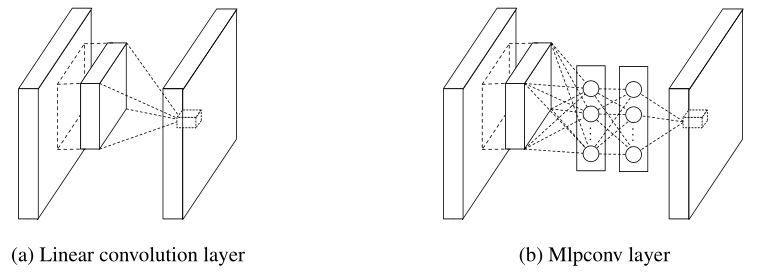
在这里插入图片描述
The mlpconv maps the input local patch to the output feature vector with a multilayer perceptron (MLP) consisting of multiple fully connected layers with nonlinear activation functions
the calculation performed by mlpconv layer:
$f_{i,j,k_1}^1=max({w_{k_1}^1}^Tx_{i,j}+b_{k_1},0)$
…
$f_{i,j,k_n}^n=max({w_{k_1}^n}^Tf_{i,j}^{n-1}+b_{k_n},0)$
n→the number of layers in the multilayer perceptron
$x_{i,j}$ →the input patch centered at location (i,j)
Notes:
different location(i,j) in first layer use the same $w_{k_1}$ , so it is different with the normal FC layer
i think it is exactly conv. layer, a neuron can be regarded as a channel
"The cross channel parametric pooling layer is also equivalent to a convolution layer with 1x1 convolution kernel"→i think it is similar idea
on the internet, i found NIN structure is implemented by the stack of conv. layers
first one is n×n, later is 1×1 kernel
so, why authors of this paper use “multiple fully connected layers”? i am confused about it…
more confusing→there is no conv. layer before the 1×1 conv. layer in GoogLeNet, different with the structure of NIN. how can 1×1 conv. layer increase the representational power?

More Confusion

in addition to the question i mentioned above, i have plenty of confusion about this paper, especially the part of “3 Motivation and High Level Consideration”.
crying cat.jpg
The Inception architecture→approximate a sparse structure implied by Provable Bounds for Learning Some Deep Representations
Their main result states that if the probability distribution of the data-set is representable by a large, very sparse deep neural network, then the optimal network topology can be constructed layer by layer by analyzing the correlation statistics of the activations of the last layer and clustering neurons with highly correlated outputs.
however, i have not found “the optimal network topology” in that paper. what’s more, i can not find the relation of the inception module and sparsity.