前言

正则化在机器学习和深度学习中都是很重要的技巧，其核心思想是通过偏差的增加来换取方差的减少----用训练误差的增大来换取泛化误差的减小。
实现正则化主要有两类策略：
1）向模型添加限制参数的额外约束
2）向目标函数增加额外项来对参数值进行软约束
常见的L1和L2正则化都是使用的第二种策略

L2正则化简介

L2正则化项：
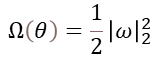
在这里插入图片描述
不考虑偏置参数，添加L2正则化之后的目标函数变成：

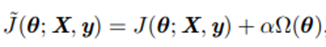
其中 *J(θ; X, y)*是原来的目标函数，α是决定正则化强度的系数。
其对应梯度如下：

使用梯度下降法更新权值的公式：

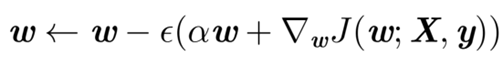
合并 $\omega$ 可得：

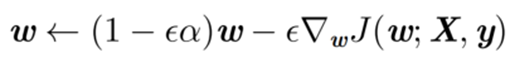
由此式可看出，加入正则项后会引起学习规则的修改，在每步执行梯度更新之前会先收缩权重向量。

下面我们从线性代数和图像两个方面来理解L2正则化的作用

线性代数角度

首先考虑无正则化时的情况：
令 $w^*$ 点为左右点，即 $\omega$ * = $argmin_w$ $J (W)$ ，并在 $w^*$ 的邻域对目标函数做二次近似（二阶泰勒展开，舍去余项）：
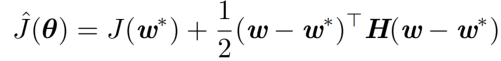
在这里插入图片描述
其中H是目标函数的Hessian矩阵，因为 $w^*$ 点为最优点，梯度为0，故上式没有一阶项。
上式对 $\omega$ 求偏导可得其梯度，并且梯度为0：

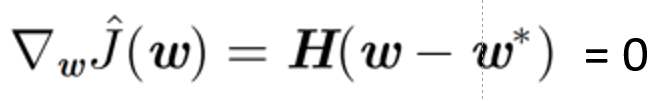
现在考虑添加正则项之后：
使用 $\omega'$ 表示此时的最优点：
$\alpha \omega' + H(\omega' - \omega^*) = 0$
$\alpha I)\omega' = H\omega^*$
$\omega' = (H + \alpha I)^{-1} H \omega^*$ 式(1)

可以看到， $\omega'$ 是由 $\omega^*$ 左乘一个矩阵得到的。
那么左乘一个矩阵会有什么影响呢？我们可以做这样一个实验：

研究单位向量u左乘矩阵A，其中矩阵A有两个标准正交的特征向量，分别是对应特征值为 $\lambda_1$ 的 $v^{(1)}$ ，以及对应特征值为 $\lambda_2$ 的 $v^{(2)}$ ；
向量u可取任意方向，画出所有的单位向量 $\in R_2$ 的顶点集合，构成一个单位圆（下图左侧）；画出所有的Au的顶点集合（下图右侧）
在这里插入图片描述
可见，左乘A的结果是对不同方向的u进行了不同程度的拉伸变换，具体来说就是，在A的特征向量 $v^{(i)}$ 方向拉伸了 $\lambda_i$ 倍。

在机器学习研究的范畴内，Hessian矩阵通常是实对称的，故可以被正交矩阵Q相似对角化：
$Q\Lambda Q^T$ 式（2）

有了以上结论，我们继续来探究 $\omega'$ 和 $\omega^*$ 的关系:
将式（2）带入式（1）并化简：
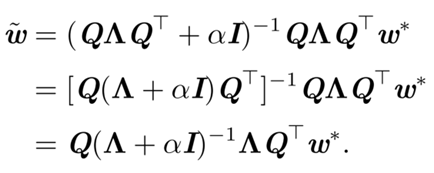
在这里插入图片描述
其中 $Q(\Lambda + \alpha I)^{-1}$ $\Lambda Q^T$ 是一个矩阵，其特征向量和H矩阵相同，其特征值由下式给出：
$\frac {\lambda_i} {\lambda_i + \alpha}$ 式（3）
根据之前的左乘矩阵收缩性的结论，我们可以得出：
正则化之后的最优权重 $\omega'$ 是将正则化之前的 $\omega^*$ 沿Hessian矩阵的特征向量的方向缩放的结果。
具体来说，根据 $\frac {\lambda_i} {\lambda_i + \alpha}$ 因子缩放与H第i个特征向量同向的 $\omega^*$ 的分量。

小结

根据缩放因子可知，沿着H特征值大的方向（如 $\lambda_i$ >> $\alpha$ ）正则化的影响小，而 $\lambda_i$ << $\alpha$ 的分量将会收缩到几乎为0.

从图像角度直观理解

回顾正则化之后的目标函数：
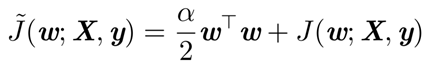
在这里插入图片描述
其中包含两项，一项是原始的目标函数，另一项是正则化项。我们的优化目标是找到最小的目标函数，所以两项都应该尽量小。
我们做如下图：

实线椭圆表示没有正则化目标的等值线， $\omega^*$ 在w1方向变化慢，在w2方向变化快；虚线圆圈表示 L2正则化项的等值线；在 $\omega'$ 点，这两个竞争目标达到平衡.
由图可以看到，w1方向的坐标被压缩到接近0的位置，而w2方向几乎没有被压缩。

补充

Hessian矩阵与方向二阶导数的关系
这是我做的ppt的截图
我们可以根据线性代数法推导出的结论来说明图像中w1轴被压缩的原因：
w1方向 $\omega^*$ 变化慢，对应方向二阶导数较小，在此方向上的H矩阵的特征值也小，根据之前的结论，H矩阵特征值小的方向上 $\omega^*$ 的分量被压缩，这就解释了图像所反映的现象。