更新中...
8.1 个体与集成
集成学习 (ensemble learning)= 多分类器系统(multi-classifier system)= 基于委员会的学习(committee-based learning): 构建并结合多个学习器, 完成学习任务.
集成学习结构:
1. 产生一组个体学习器
2. 用某种策略结合它们
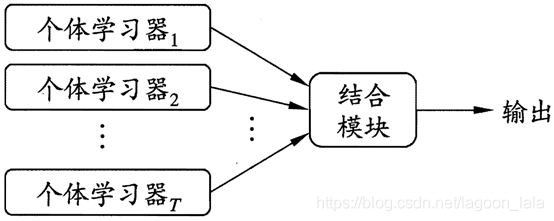
?个体学习器(individual learner): 由现有学习算法从训练数据产生.
1. 同质(homogeneous)
?????? 基学习器(base learner): 个体学习器/弱学习器" (weak learner)(实际会用较强学习器)
?????? 基学习算法(base learning algorithm): 个体学习器对应算法.
2. 异质(heterogenous)
?????? 组件学习器(component learner)=个体学习器
好的集成=个体学习器准确性+多样性(diversity)
准确性与多样性存在冲突. 准确性至少不能差于弱学习器(50%).
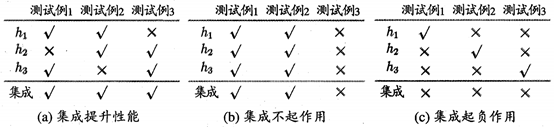
集成学习对比单一学习器例子:
二分类任务,三个分类器在三个测试样本, 通过投票法(voting)产生集成学习的结果.
1. 准确+多样. 每个分类器精度66.6%, 集成学习精度100%
2. 准确+不多样. 每个分类器精度66.6%, 集成学习精度66.6%
3. 不准确+多样. 每个分类器精度33.3%, 集成学习精度0%
集成学习方法
1. Boosting. 个体学习器的生成方式: 个体学习器间强依赖、必须串行生成的序列化方法.
2. Bagging, 随机森林(Random Forest). 个体学习器的生成方式: 个体学习器间无强依赖、可同时生成的并行化方法.
集成错误率
| 符号 | 含义 |
| $$ h_{i}(\boldsymbol{x})\in \{-1,+1\} $$ | 基分类器i对x的预测标记 |
| $$ y=f(\boldsymbol{x})\in \{-1,+1\} $$ | x的真实标记 |
| $$ \epsilon $$ | 错误率, 预测与真实不一致的概率 |
hi基分类器错误率
$$ P\left(h_{i}(\boldsymbol{x}) \neq f(\boldsymbol{x})\right)=\epsilon $$
通过投票法结合T个基分类器,若有超过半数的基分类器预测+1,则集成分类就+1:
| $$ \sum_{i=1}^{T} h_{i}(\boldsymbol{x})>0 $$ | 基分类器中预测1超过半数 |
| $$ \sum_{i=1}^{T} h_{i}(\boldsymbol{x})<0 $$ | 基分类器中预测-1超过半数 |
(投票分类)集成结果
$$ H(\boldsymbol{x})=\text{sgn}\left(\sum_{i=1}^{T} h_{i}(\boldsymbol{x})\right) $$
假设基分类器的错误率相互独立,则由Hoeffding不等式,集成预测的错误率为:
$$ \begin{aligned} P(H(\boldsymbol{x}) \neq f(\boldsymbol{x})) &=\sum_{k=0}^{\lfloor T / 2\rfloor} \left( \begin{array}{c}{T} \\ {k}\end{array}\right)(1-\epsilon)^{k} \epsilon^{T-k} \\ & \leq \exp \left(-\frac{1}{2} T(1-2 \epsilon)^{2}\right) \end{aligned} ?$$
上式分类器数T越大, 集成的错误率越小,最终趋向于零.
但该式的假设(基学习器误差相互独立)并不成立, 准确性和多样性存在矛盾, 无法达到这么好的效果.
错误率推导
伯努利分布: n=1时的二项分布
$$ X \sim B(1, p)\\ P(X=x)= \begin{cases} p, & \text {if $x=1$} \\ 1-p, & \text{if $x=0$} \end{cases}\\ E(X)=p,~ D(X)=p(1-p) ?$$
二项分布: n个独立的成功/失败试验中成功的次数的离散概率分布
$$ X \sim B(n, p)\\?\begin{align}P(X=k)=\begin{pmatrix} n \\ k \\ \end{pmatrix} p^k(1-p)^{n-k} ,?? & \;\;\;\;\; \text{for $0 \leq k \leq n$}\end{align}\\ E(X)=np,~ D(X)=np(1-p) $$
在集成学习中, 每一个分类器分类正确的次数xi:
$$ x_i\sim B(1, 1-\mathrm{\epsilon})(i=1,2,3,...,\mathrm{T}) $$
T个基分类器分类正确的次数X:
$$ \mathrm{X}=\sum_{i=1}^{\mathrm{T}} x_i \sim B(\mathrm{T}, 1-\mathrm{\epsilon})\\ \mathbb{E}(X)=\sum_{i=1}^{\mathrm{T}}\mathbb{E}(x_i)=(1-\epsilon)T $$
Hoeffding不等式指随机变量的和与其期望值偏差的概率上限.
根据习题8.1给出的Hoeffding不等式
抛硬币正面朝上的概率为p, 反面朝上的概率为1-p. H(n)代表抛n次硬币所得正面朝上的次数,则最多k次正面朝上的概率(=1次成功~k次成功的概率之和)为:
$$ P(H(n)\leq k)=\sum_{i=0}^k\begin{pmatrix} n \\ i \\ \end{pmatrix} p^i(1-p)^{n-i} ??$$
Hoeffding不等式:
$$ 当\delta>0, k=(p-\delta)n, \\?P(H(n)\leq (p-\delta)n)\leq e^{-2\delta^2n} $$
将集成错误率代入Hoeffding不等式时, 将代入几个具体符号:
| Hoeffding符号 | 错误率公式符号 | 含义 |
| $$ n $$ | $$ T $$ | n次实验; T个分类器 |
| $$ H(n)\leq k $$ | $$ H(n)\leq \lfloor T/2 \rfloor \\ \Leftrightarrow H(\boldsymbol{x}) \neq f(\boldsymbol{x}) $$ | 最多k次成功的概率; 当正确的基分类器个数不超过?T/2?, 即集成后预测错误 |
| $$ i $$ | $$ k $$ | i次实验成功; k个分类器预测正确 |
| $$ p $$ | $$ 1-\epsilon $$ | 单次实验成功概率p; 基分类器正确率1-? |
则Hoeffding不等式:
$$ 当\delta>0, k=(p-\delta)n?\lfloor T/2\rfloor =(1-\epsilon-\delta)T, \\?P(H(T)\leq (1-\epsilon-\delta)T)\leq e^{-2\delta^2 T} $$
根据条件?T/2? =(1-?-δ)T整理δ, 代入原不等式即可解出错误率的Hoeffding不等式.
首先整理δ:
$$ \lfloor T/2\rfloor =(1-\epsilon-\delta)T\\ \Rightarrow \delta=1-\epsilon-\frac{\lfloor T/2\rfloor}{T} $$
其中弱分类器正确率1??>1/2, 且根据向下取整性质:
$$ \begin{align} 1-\epsilon&> \frac{1}{2},\frac{\lfloor T/2\rfloor}{T}\leq \frac{1}{2}\\ \Rightarrow \delta&=1-\epsilon-\frac{\lfloor T/2\rfloor}{T} \\?&\geq 1-\epsilon-\frac{1}{2}>0?\end{align} $$
δ代入原不等式即:
$$? \begin{align} P(H(T)\leq \lfloor T/2\rfloor)& \leq e^{-2\delta^2 T}\\ & \leq e^{-2(1-\epsilon-\frac{1}{2})^2 T}=e^{ -\frac{T}{2} (1-2 \epsilon)^{2}} \end{align} ?$$