目录
1.PCA简介
主成分分析算法(PCA)是最常用的线性降维方法,它的目标是通过某种线性投影,将高维的数据映射到低维的空间中,并期望在所投影的维度上数据的信息量最大(方差最大),以此使用较少的数据维度,同时保留住较多的原数据点的特性。
PCA降维的目的,就是为了在尽量保证“信息量不丢失”的情况下,对原始特征进行降维,也就是尽可能将原始特征往具有最大投影信息量的维度上进行投影。将原特征投影到这些维度上,使降维后信息量损失最小。
1:获得数据
2:求平均值
3:各数据减平均值
4:计算数据的协方差矩阵
5:计算协方差矩阵的特征值、特征向量
6:把原数据进行投影 2.照片要求
? ? 30个人,每人拍摄10张正脸照片,取每个人的7张照片,共210张作为训练数据。那么每个人剩下的3张照片,计算机还没有看过,就可以在计算机认识了每一个人之后用来考研计算机是否真的能够正确识别图像中的人是谁。
这是我创造的30个人的训练集文件,每个trainxx 下又包含7张照片。
?
这是我创造的30个人的测试集文件,每个testxx 下又包含3张照片。
?
3.创建训练人脸库的特征脸空间
????????3.1:创建所有训练样本组成的 M×N 矩阵
?创建所有训练样本组成的 M×N 矩阵 trainFaceMat。M 为样本个数,N 为一 个训练样本? ? ? ? ? ? ? ? ?图像所有像素按行相连的像素值,在本次实验中,?M = 人数(使用的30个人的人脸数据) * 7(每人7张照片)= 210。
N = 像素点的个数,比如说一张照片大小为 10 * 10, N就为100。在本次实验中,我们把每个人的照片都处理成128 * 128,因此N = 16384。
# 对于每一张照片,首先创建一个列表list,存储本张照片的16384个灰度值,
# 当一个list存储完16384个灰度值后,将list添加至bigList。
# 依次循环210次, bigList就存储了210张照片的灰度值了。
'''
注:这里有一处细节,就是我是在读入每一张照片时,是新创建的列表list。
而不是在最开始创建list,然后每次读入照片时使用.clear()清空list。
这里涉及到Python中浅复制的知识,是因为bigList使用append的时候,
是浅复制的状态,如果之后对列表list操作bigList也会被修改,这样的话
最后bigList存储的全为最后一张照片的灰度值。
'''
# 最后使用numpy中的函数,将列表bigList转换为矩阵。
bigList = []
# 导入人脸模型库
faceCascade = cv2.CascadeClassifier(r'C:\Python\haarshare\haarcascade_frontalface_alt.xml')
# 遍历30个人
for i in range(1, 31):
# 遍历每个人的7张照片
for j in range(1, 8):
list = []
# 直接读入灰度照片
image = cv2.imread("C:\\Users\\tangyitao\\Pictures\\Saved Pictures\\trainFace\\train"
+ str(i) + "\\train" + str(i) + "" + str(j) + ".jpg", 0)
faces = faceCascade.detectMultiScale(image, 1.3, 5)
for (x, y, w, h) in faces:
# 裁剪人脸区域为 128 * 128 大小
cutResize = cv2.resize(image[y:y + h, x:x + w], (128, 128),
interpolation=cv2.INTER_CUBIC)
# 遍历图片行数
for x in range(cutResize.shape[0]):
# 遍历图片每一行的每一列
for y in range(cutResize.shape[1]):
# 将每一处的灰度值添加至列表
list.append(cutResize[x, y])
bigList.append(list)
print("\n\ntrainFaceMat ")
trainFaceMat = numpy.mat(bigList) # 得到训练样本矩阵
print("trainFaceMat.shape[0] ",trainFaceMat.shape[0])
print("trainFaceMat.shape[1]",trainFaceMat.shape[1])
print(trainFaceMat)
运行结果:
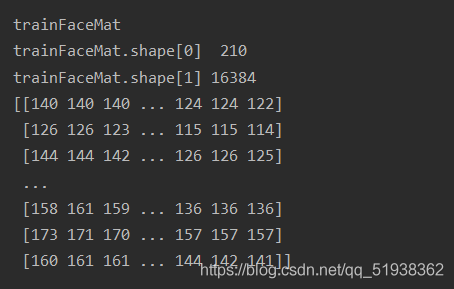
?????????3.2:计算训练样本的平均值矩阵
?计算训练样本的平均值矩阵meanFaceMat,该矩阵大小为1 * N。1 * N 就代表目前算出? ? ? ? ? ? ? ? ? ? ?来的平均值矩阵是 一张 人脸的数据,这张平均脸其实就是把上面的 M * N 的矩阵? ? ? ? ? ? ?trainFaceMat平均化,把这 M 张照片的每一个位置对应的数值加起来,然后再除以 M。可以理解为把一 个 M * N 的二维数组的每一列都加起来,变成一个 1 * N 的数组,然后这个数组的每一? ? ? ? ?位都除以 M,最后得到一个 1 * N 的平均值脸。
# numpy中有相关函数,直接调用即可
# axis = 0代表计算每一列的平均值
# axis = 1代表计算每一行的平均值
meanFaceMat = numpy.mean(trainFaceMat, axis=0) # 每一列的和除行数,得到平均值
print("meanFaceMat \n\n")
print("meanFaceMat.shape[0] ",meanFaceMat.shape[0])
print("meanFaceMat.shape[1] ",meanFaceMat.shape[1])
print(meanFaceMat)
?运行结果:

?
????????3.3:去除平均值,得到规格化后的训练样本矩阵
计算规格化后的训练样本矩阵 normTrainFaceMat,矩阵大小为 M×N。用我们一开始得到的 M*N 的矩阵 trainFaceMat 减去我们的平均脸矩阵meanFaceMat,即计算出我每个人的数据跟这个平均脸的差异,我们把计算结果成为差值矩阵。
# trainFaceMat 大小为 M * N, meanFaceMat 大小为 1 * N
# 可直接相减
normTrainFaceMat = trainFaceMat - meanFaceMat
print("\n\n normTrainFaceMat")
print("normTrainFaceMat.shape[0] ",normTrainFaceMat.shape[0])
print("normTrainFaceMat.shape[1] ",normTrainFaceMat.shape[1])
print(normTrainFaceMat)
运行结果:
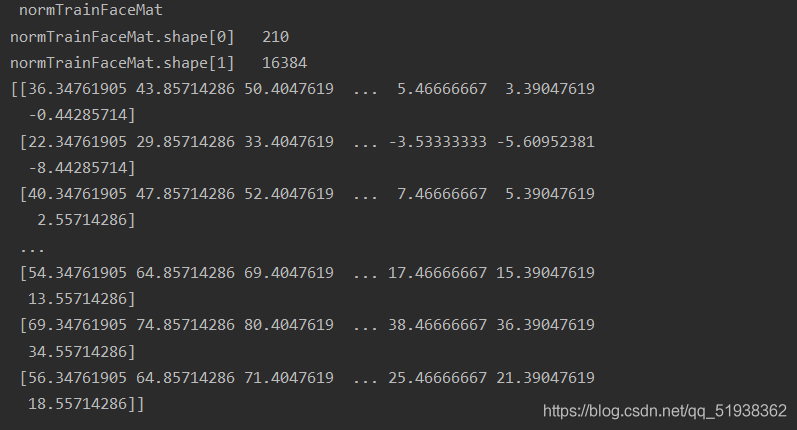
?
covariance = numpy.cov(normTrainFaceMat)计算 协方差矩阵covariance的特征值eigenvalue和特征向量featurevector。
# 求得协方差矩阵的特征值和特征向量
eigenvalue, featurevector = numpy.linalg.eig(covariance) sorted_Index = numpy.argsort(eigenvalue)????????3.7:保留前K个最大的特征值对应的特征向量
topk_evecs = featurevector[:,sorted_Index[:-140-1:-1]]函数计算得到的矩阵 eigenface 大小为 N×m,每一列是一个长度为 N 的特征脸,共 m 列。
eigenface = numpy.dot(numpy.transpose(normTrainFaceMat), topk_evecs)eigen_train_sample = numpy.dot(normTrainFaceMat, eigenface)?eigen_train_sample 为投影样本矩阵,大小为 M×m,每一行为一个训练样本图 像在特征脸空间的投影。由于 m<<N,经过投影可获得更能描述训练样本图像特征的描述。
4.人脸识别
# 主要思想和第一步计算trainFaceMat差不多,这里只需要添加一张照片的数据
list = []
faceCascade = cv2.CascadeClassifier(r'C:\Python\haarshare\haarcascade_frontalface_alt.xml')
# fileName 为待识别图片的文件名,读入灰度人脸
image = cv2.imread(fileName, 0)
faces = self.faceCascade.detectMultiScale(self.image, 1.3, 5)
for (x, y, w, h) in self.faces:
cut = image[y:y + h, x:x + w]
# 处理成 128 * 128大小的人脸
cutResize = cv2.resize(cut, (128, 128), interpolation=cv2.INTER_CUBIC)
for x in range(cutResize.shape[0]):
for y in range(cutResize.shape[1]):
list.append(cutResize[x, y])
testFaceMat = numpy.mat(list)?????????4.2:去除平均值,得到规格化后的识别样本矩阵
# 这里减的meanFaceMat 和计算normTrainFaceMat 的meanFaceMat是同一个变量
normTestFaceMat = testFaceMat - meanFaceMat# 和计算 eigen_train_sample相同,用规格化矩阵去点乘 eigenface即可。
eigen_test_sample = numpy.dot(normTestFaceMat, eigenface)# 以 eigen_train_sample[0]与eigen_test_sample的欧式距离赋值 minDistance
minDistance = numpy.linalg.norm(eigen_train_sample[0], eigen_test_sample)
# num 记录训练集中第几个人与待识别人为同一人
num = 1
# 遍历 eigen_train_sample 的每一行,在此处,eigen_train_sample.shape[0] = 210。
for i in range(1, eigen_train_sample.shape[0]):
distance = numpy.linalg.norm(eigen_train_sample[i], eigen_test_sample)
if minDistance > distance:
minDistance = distance
# 30个人中,每个人有7张照片,i是记录的第几张照片
# 因此记录第几个人的num为 i // 7 + 1。
num = i // 7 + 1到这一步,人脸识别的算法就完了,后面就自己去写一些界面来丰富自己的人脸识别,下面附上几张图测试一下此算法。
?

?
因为我使用的所有图片都是学长学姐们自己拍摄的,所以为了保护肖像权······嘿嘿…^o^懂得都懂。?
从发型看还是能看出来是同一个人吧哈哈哈。
在本博客所写代码中,不能实现待识别人脸不在训练集中的提示,他会查找到一张跟欧氏距离最小的照片显示。另因为算法本身就较为简陋,所以识别成功率不是很高。
注:此博客是在我的一位学长写的任务书下完成,文章中部分提及到任务书中的内容,在此感谢那位学长。
?
?
?
?
?
? ? ?