第五章 深度学习用于计算机视觉
5.1 卷积神经网络简介
5.1.1 卷积神经网络对 MNIST 分类
使用卷积神经网络对 MNIST 数字进行分类,在第 2 章用密集连接网络做过(当时的测试精度为 97.8%)。它是 Conv2D 层和 MaxPooling2D 层的堆叠。
-
实例化一个小型的卷积神经网络
from keras import layers from keras import models model = models.Sequential() model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1))) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu'))卷积神经网络接收形状为
(image_height, image_width, image_channels)的输入张量(不包括批量维度)。第一层传入参数input_shape=(28, 28, 1)来完成此设置。>>> model.summary() _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_1 (Conv2D) (None, 26, 26, 32) 320 _________________________________________________________________ max_pooling2d_1 (MaxPooling2D) (None, 13, 13, 32) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 11, 11, 64) 18496 _________________________________________________________________ max_pooling2d_2 (MaxPooling2D) (None, 5, 5, 64) 0 _________________________________________________________________ conv2d_3 (Conv2D) (None, 3, 3, 64) 36928 ================================================================= Total params: 55,744 Trainable params: 55,744 Non-trainable params: 0每个
Conv2D层和MaxPooling2D层的输出都是一个形状为(height, width,channels)的 3D 张量。通道数量由传入Conv2D层的第一个参数所控制(32 或 64)。 -
在卷积神经网络上添加分类器
model.add(layers.Flatten()) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(10, activation='softmax'))在进入两个 Dense 层之前,形状 (3, 3, 64) 的输出被展平为形状 (576,) 的向量。
>>> model.summary() _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= conv2d_1 (Conv2D) (None, 26, 26, 32) 320 _________________________________________________________________ max_pooling2d_1 (MaxPooling2D) (None, 13, 13, 32) 0 _________________________________________________________________ conv2d_2 (Conv2D) (None, 11, 11, 64) 18496 _________________________________________________________________ max_pooling2d_2 (MaxPooling2D) (None, 5, 5, 64) 0 _________________________________________________________________ conv2d_3 (Conv2D) (None, 3, 3, 64) 36928 _________________________________________________________________ flatten_1 (Flatten) (None, 576) 0 _________________________________________________________________ dense_1 (Dense) (None, 64) 36928 _________________________________________________________________ dense_2 (Dense) (None, 10) 650 ================================================================= Total params: 93,322 Trainable params: 93,322 Non-trainable params: 0 -
在 MNIST 图像上训练卷积神经网络
from keras.datasets import mnist from keras.utils import to_categorical (train_images, train_labels), (test_images, test_labels) = mnist.load_data() train_images = train_images.reshape((60000, 28, 28, 1)) train_images = train_images.astype('float32') / 255 test_images = test_images.reshape((10000, 28, 28, 1)) test_images = test_images.astype('float32') / 255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy']) model.fit(train_images, train_labels, epochs=5, batch_size=64)在测试数据上对模型进行评估。
>>> test_loss, test_acc = model.evaluate(test_images, test_labels) >>> test_acc 0.9912999868392944 -
整体代码
from tensorflow.keras.datasets import mnist from tensorflow.keras.utils import to_categorical from tensorflow.keras import layers from tensorflow.keras import models (train_images, train_labels), (test_images, test_labels) = mnist.load_data() train_images = train_images.reshape((60000, 28, 28, 1)) train_images = train_images.astype('float32') / 255 test_images = test_images.reshape((10000, 28, 28, 1)) test_images = test_images.astype('float32') / 255 train_labels = to_categorical(train_labels) test_labels = to_categorical(test_labels) model = models.Sequential() model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1))) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.MaxPooling2D((2, 2))) model.add(layers.Conv2D(64, (3, 3), activation='relu')) model.add(layers.Flatten()) model.add(layers.Dense(64, activation='relu')) model.add(layers.Dense(10, activation='softmax')) model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy']) model.fit(train_images, train_labels, epochs=5, batch_size=64) test_loss, test_acc = model.evaluate(test_images, test_labels)结果是:
>>> test_acc 0.99080000000000001
5.1.2 卷积运算
-
D e n s e 层 \color{red}Dense 层 Dense层从输入特征空间中学到的是 全 局 模 式 \color{red}全局模式 全局模式,而 卷 积 层 \color{red}卷积层 卷积层学到的是 局 部 模 式 \color{red}局部模式 局部模式。
-
卷积神经网络具有以下两个性质:
- 卷积神经网络学到的模式具有
平
移
不
变
性
(
t
r
a
n
s
l
a
t
i
o
n
??
i
n
v
a
r
i
a
n
t
)
\color{red}平移不变性(translation\;invariant)
平移不变性(translationinvariant)。这使得卷积神经网
络在处理图像时可以高效利用数据(因为 视 觉 世 界 从 根 本 上 具 有 平 移 不 变 性 \color{red}视觉世界从根本上具有平移不变性 视觉世界从根本上具有平移不变性),它只需要更少的训练样本就可以学到具有泛化能力的数据表示。 - 卷积神经网络可以学到
模
式
的
空
间
层
次
结
构
(
s
p
a
t
i
a
l
??
h
i
e
r
a
r
c
h
i
e
s
??
o
f
??
p
a
t
t
e
r
n
s
)
\color{red}模式的空间层次结构(spatial\;hierarchies\;of\;patterns)
模式的空间层次结构(spatialhierarchiesofpatterns)。卷积神经网络可以有效地学习越来越复杂、越来越抽象的视觉概念(因为
视
觉
世
界
从
根
本
上
具
有
空
间
层
次
结
构
\color{red}视觉世界从根本上具有空间层次结构
视觉世界从根本上具有空间层次结构)。
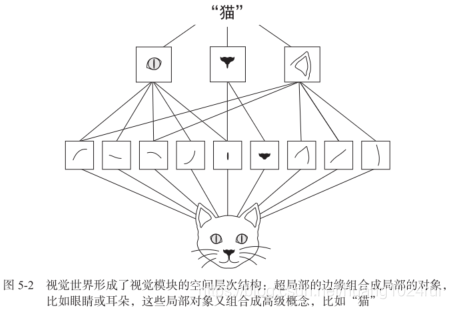
- 卷积神经网络学到的模式具有
平
移
不
变
性
(
t
r
a
n
s
l
a
t
i
o
n
??
i
n
v
a
r
i
a
n
t
)
\color{red}平移不变性(translation\;invariant)
平移不变性(translationinvariant)。这使得卷积神经网
-
特 征 图 ( f e a t u r e ?? m a p ) \color{red}特征图(feature\;map) 特征图(featuremap)
- 定义: 深度轴的每个维度都是一个
特
征
\color{red}特征
特征(或
过
滤
器
\color{red}过滤器
过滤器),而 2D 张量
output[:, :, n]是这个过滤器在输入上的响应的二维空间 图 ( m a p ) \color{red}图(map) 图(map)。 - 应用:
- 输入卷积中的: 包含两个空间轴(高度和宽度)和一个深度轴(也叫通道轴)的 3D 张量,其卷积也叫 特 征 图 ( f e a t u r e ?? m a p ) \color{red}特征图(feature\;map) 特征图(featuremap)。
- 从卷积中输出的: 卷积运算从输入特征图中提取图块,并对所有这些图块应用相同的变换,生成 输 出 特 征 图 ( o u t p u t ?? f e a t u r e ?? m a p ) \color{red}输出特征图(output\;feature\;map) 输出特征图(outputfeaturemap)。该输出特征图仍是一个 3D 张量,具有宽度和高度,其深度是输出深度是层的参数,每层代表代表 过 滤 器 ( f i l t e r ) \color{red}过滤器(filter) 过滤器(filter)。
- 定义: 深度轴的每个维度都是一个
特
征
\color{red}特征
特征(或
过
滤
器
\color{red}过滤器
过滤器),而 2D 张量
-
卷积关键参数:
- 从 输 入 中 提 取 的 图 块 尺 寸 \color{red}从输入中提取的图块尺寸 从输入中提取的图块尺寸:这些图块的大小通常是 3 × 3 3×3 3×3 或 5 × 5 5×5 5×5。本例中为 3 × 3 3×3 3×3。
- 输 出 特 征 图 的 深 度 \color{red}输出特征图的深度 输出特征图的深度:卷积所计算的过滤器的数量。本例第一层的深度为 32 32 32,最后一层的深度是 64 64 64。
-
卷积的工作原理
- 开始:在 3D 输入特征图上
滑
动
(
s
l
i
d
e
)
\color{red}滑动(slide)
滑动(slide)这些
3
×
3
3×3
3×3或
5
×
5
5×5
5×5的窗口,在每个可能的位置停止并提取周围特征的 3D 图块[
形状为 (window_height, window_width, input_depth)]。 - 然后,每个 3D 图块与学到的同一个权重矩阵[叫作
卷
积
核
(
c
o
n
v
o
l
u
t
i
o
n
k
e
r
n
e
l
)
\color{red}卷积核(convolution kernel)
卷积核(convolutionkernel)]做
张
量
积
\color{red}张量积
张量积,转换成形状为
(output_depth,)的 1D 向量。 - 最后,对所有这些向量进行空间重组,使其转换为形状为
(height, width, output_depth)的 3D 输出特征图。输出特征图中的每个空间位置都对应于输入特征图中的相同位置。
如图所示:
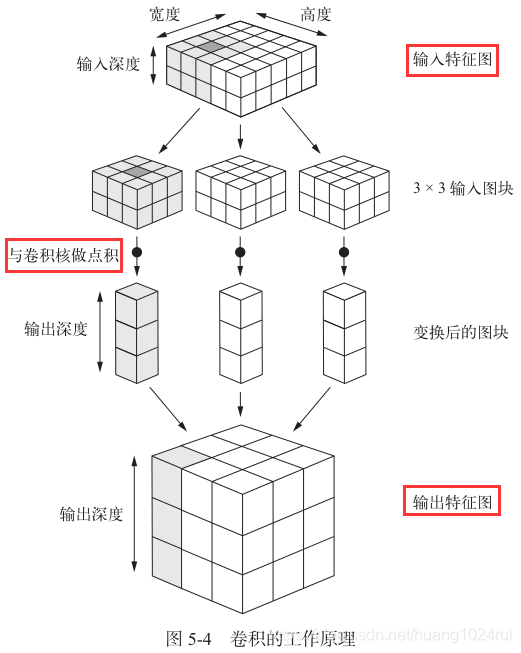
输 出 的 宽 度 和 高 度 可 能 与 输 入 的 宽 度 和 高 度 不 同 \color{red}输出的宽度和高度可能与输入的宽度和高度不同 输出的宽度和高度可能与输入的宽度和高度不同。不同的原因可能有两点:
- 边 界 效 应 \color{red}边界效应 边界效应,可以通过对输入特征图进行填充来抵消。
- 使 用 了 步 幅 ( s t r i d e ) \color{red}使用了步幅(stride) 使用了步幅(stride),稍后会给出其定义。
- 开始:在 3D 输入特征图上
滑
动
(
s
l
i
d
e
)
\color{red}滑动(slide)
滑动(slide)这些
3
×
3
3×3
3×3或
5
×
5
5×5
5×5的窗口,在每个可能的位置停止并提取周围特征的 3D 图块[
5.1.3 边界效应与填充
- 边界效应定义:
假设用 3 × 3 3×3 3×3的特征图 进行卷积Con2,开始的输入尺寸为 28 × 28 28×28 28×28,经过第一个卷积层之后尺寸变为 26 × 26 26×26 26×26。 - 填充的定义:
填充是在输入特征图的每一边 添 加 适 当 数 目 的 行 和 列 \color{red}添加适当数目的行和列 添加适当数目的行和列,使得每个输入方块都能作为 卷 积 窗 口 的 中 心 \color{red}卷积窗口的中心 卷积窗口的中心。 - 对于 Conv2D 层,可以通过
padding参数来设置填充,这个参数有两个取值:- “
valid” 表示 不 使 用 填 充 \color{red}不使用填充 不使用填充(只使用有效的窗口位置); - “
same” 表示“ 填 充 后 输 出 的 宽 度 和 高 度 与 输 入 相 同 \color{red}填充后输出的宽度和高度与输入相同 填充后输出的宽度和高度与输入相同”。 - padding 参数的默认值为 “
valid” 。
- “
5.1.4 卷积步幅
- 卷积步幅定义:
两个连续窗口的距离是卷积的一个参数,叫作 步 幅 \color{red}步幅 步幅,默认值为 1 \color{red}1 1。 - 步幅为n的意义:
- 步幅为 n n n意味着特征图的宽度和高度都被做了 n n n倍 下 采 样 \color{red}下采样 下采样(除了边界效应引起的变化)。
- 为了 对 特 征 图 进 行 下 采 样 \color{red}对特征图进行下采样 对特征图进行下采样, 我 们 不 用 步 幅 \color{red}我们不用步幅 我们不用步幅,而是通常使用 最 大 池 化 ( m a x ? p o o l i n g ) 运 算 \color{red}最大池化(max-pooling)运算 最大池化(max?pooling)运算。
5.1.5 最大池化运算
-
最大池化的定义:
- 最大池化是 从 输 入 特 征 图 中 提 取 窗 口 , 并 输 出 每 个 通 道 的 最 大 值 \color{red}从输入特征图中提取窗口,并输出每个通道的最大值 从输入特征图中提取窗口,并输出每个通道的最大值。
- 使 用 硬 编 码 的 m a x 张 量 运 算 对 局 部 图 块 进 行 变 换 , 而 不 是 使 用 学 到 的 线 性 变 换 ( 卷 积 核 ) \color{red}使用硬编码的 max 张量运算对局部图块进行变换,而不是使用学到的线性变换(卷积核) 使用硬编码的max张量运算对局部图块进行变换,而不是使用学到的线性变换(卷积核)。
-
最大池化的作用:
- 减 少 需 要 处 理 的 特 征 图 的 元 素 个 数 \color{red}减少需要处理的特征图的元素个数 减少需要处理的特征图的元素个数.
- 通过让连续卷积层的观察窗口越来越大, 从 而 引 入 空 间 过 滤 器 的 层 级 结 构 \color{red}从而引入空间过滤器的层级结构 从而引入空间过滤器的层级结构。
因为如果只使用卷积核会造成:
- 不 利 于 学 习 特 征 的 空 间 层 级 结 构 。 \color{red}不利于学习特征的空间层级结构。 不利于学习特征的空间层级结构。
- 最 后 一 层 的 特 征 图 对 每 个 样 本 所 有 的 元 素 太 多 , 造 成 难 以 计 算 。 \color{red}最后一层的特征图对每个样本所有的元素太多,造成难以计算。 最后一层的特征图对每个样本所有的元素太多,造成难以计算。
-
实现下采样可以用:
- 步幅
padding; - 平均池。
但最大池化的效果往往比这些替代方法更好。观察不同特征的最大值(而不是平均值)能够给出更多的信息,类似SIFT算法的下采样步骤。
- 步幅