[人工智能]【CVPR 2021】基于解耦特征的目标检测知识蒸馏：Distilling Object Detectors via Decoupled Features

论文地址：

https://arxiv.org/abs/2103.14475

主要问题：

与图像分类不同的是，目标检测的知识蒸馏更加复杂，因为它往往具有具有多个损失函数，其中语义信息所依赖的特征纠缠在一起

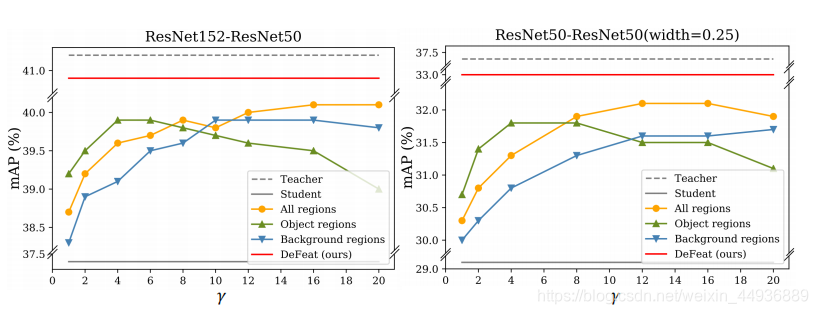
此外其他的目标检测知识蒸馏算法往往忽略了排除对象的区域的特征信息（就是背景区域的特征），而作者通过相关实验发现，只有通过背景区域特征蒸馏学生也可以显著提高学生，也就是说背景区域的特征对知识蒸馏也非常重要

这是因为通过背景区域蒸馏有效地减少了背景假阳性的数量

之前也有相关研究考虑了背景区域，但一旦将背景和前景集成在一起，蒸馏性能就会意外下降。原因可能是他们的方法直接整合了这两种区域。

从梯度的角度，作者在下图中说明了对象和背景区域之间的不一致：

左列的图像是从COCO训练集中随机选择的，右列的图像是在学生检测器中它们的neck部分特征的相应梯度

我们可以观察到，对象区域的梯度大小始终大于来自背景区域的梯度大小

因此，这提醒我们在蒸馏过程中物体区域和背景区域的不同重要性

主要思路：

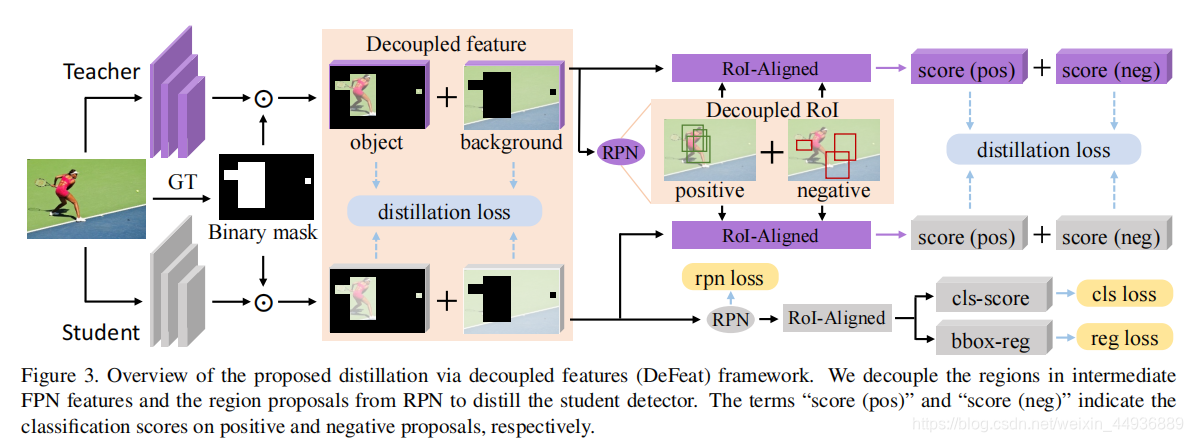
基于上述观察，作者提出了一种新的蒸馏算法，通过解耦特征（DeFeat）来学习一个更好的学生检测器

具体地说就是该算法会预处理两层解耦特征，从而将有用信息嵌入学生

作者说的两层就是从颈部（neck）的解耦特征和从分类头（head）的解耦建议区域（proposals），提取出FPN特征和RoI Align特征

前者利用GT掩码将FPN特征分为前景和背景部分，并在师生模型之间使用均方误差损失

后者的RoI Align特征也被解耦为正部分和负部分，然后利用师生模型基于RoI Align特征生成的logits计算KL散度损失

具体实现：

基本符号：

假设 $S\in R^{H\times W\times C}$ 和 $T\in R^{H\times W\times C}$ 分别是学生模型和教师模型的证件特征，基于中间特征的知识蒸馏损失就可以写作：

$L_{fea}=\frac{\gamma }{2N}{\sum }_{h=1}^H{\sum }_{w=1}^W{\sum }_{c=1}^{C}I(?(S_{h,w,c})?T_{h,w,c}{)}^2$

其中$N=HWC$为元素总数，用$\gamma$控制蒸馏损失的大小，$?$表示自适应层（用来降维），$I$表示模拟掩模（imitation mask），即中的高斯掩模或者细粒度掩模

在以前的工作中，只考虑对象区域或均匀地提取整个特征图，这些方法中的掩模可以看作是一个全是1的张量

给定RPN输出的K个建议区域，分类头需要计算所有proposals的软标签，通过软预测进行的蒸馏可以表述为：

$L_{}cls=\frac{1}{K}{\sum }_{i=1}^K{L}_{CE}(y_i^s,Y_i)+\frac{\lambda }{K}{\sum }_{i=1}^K{L}_{KL}(y_i^s,y_i^t)$

其中 $L_{CE}$ 是交叉熵损失，$L_{KL}$ 是KL散度，$Y_i$ 是第 $i$ 个proposal的真实标签，$y_i^s,y_i^t$ 分别是学生模型和教师模型的预测输出

这样总损失就可以写作：

$L=L_{fea}+L_{cls}+L_{reg}+L_{rpn}$

Decouple Intermediate Features in Distillation：

作者通过实验发现仅通过背景区域进行蒸馏仍然能获得与仅通过对象区域进行蒸馏相当的结果

以此得出的结论是，中间特征中的背景区域可以补充对象区域，并进一步有助于训练学生检测器，但剩下的问题是如何在蒸馏中适当地整合这两种区域

基于上述观察，作者建议通过解耦特征对学生模型进行蒸馏

给定$H\times W$大小的中间特征，我们首先根据真值框$B$生成一个二进制掩模 $M$：

$M_{i,j}=1[(i,j)\in B]$

其中 M ∈ { 0 , 1 } H × W M\in\{0,1\}^{H×W} M∈{0,1}H×W，位置 $(i,j)$ 的值为 $1$ 表示它属于前景，$0$ 则表示背景

更具体地说就是，如果检测器包含可以输出多层次特征的特征金字塔网络（FPN），我们将每个真值框分配到相应的层次，并相应地生成掩模 $M$

然后我们就可以使用生成的二进制掩码来解耦颈部特征，如图所示：

中间特征蒸馏的公式为：
$$\begin{array}{rl}{L}_{fea}=& \frac{{\alpha }_{obj}}{2N_{obj}}\sum _{h=1}^H\sum _{w=1}^W\sum _{c=1}^C{M}_{h,w}(?(S_{h,w,c})?T_{h,w,c}{)}^2\\ & +\frac{{\alpha }_{bg}}{2N_{bg}}\sum _{h=1}^H\sum _{w=1}^W\sum _{c=1}^C(1?M_{h,w})(?(S_{h,w,c})?T_{h,w,c}{)}^2\end{array}$$

其中 $N_{obj}=C{\sum }_{h=1}^H{\sum }_{w=1}^W{M}_{w,h}$ 是正样本区域元素数目， $N_{bg}=C{\sum }_{h=1}^H{\sum }_{w=1}^W(1?M_{w,h})$ 是负样本区域元素数目，${\alpha }_{obj}$和${\alpha }_{bg}$分别是前景和背景区域的损失系数

Decouple Region Proposals in Distillation：

作者通过实验发现，正样本的蒸馏损失始终比负样本的蒸馏损失要大。而且如果它们没有适当地平衡，负样本产生的小梯度可能会淹没在正样本产生的大梯度中，从而限制了进一步的细化

因此作者建议在提取分类头时，将region proposal解耦为正样本和负样本，以达到最优收敛性

作者将教师模型产生的区域建议输入教师和学生的头部，以生成$p^t$和$p^s$的类别预测

正样本和负样本在作者提出的方法中单独处理

假设正样本输出logits为 $z$，作者通过温度参数$T_{obj}$对教师模型和学生模型的预测进行软化：

$p^{s,T_{obj}}(c|{\theta }^s)=\frac{exp(z_c^s/T_{obj})}{{\sum }_{j=1}^{C}exp(z_j^s/T_{obj})},c\in Y$

$p^{t,T_{obj}}(c|{\theta }^t)=\frac{exp(z_c^t/T_{obj})}{{\sum }_{j=1}^{C}exp(z_j^t/T_{obj})},c\in Y$

负样本则类似的通过 $T_{bg}$ 进行处理

最终蒸馏损失就用 KL 散度，写作：

$$\begin{array}{rl}{L}_{fea}=& \frac{{\beta }_{obj}}{K_{obj}}\sum _{i=1}^K{b}_i{L}_{KL}(p_i^{s,T_{obj}},p_i^{t,T_{obj}})\\ & +\frac{{\beta }_{bg}}{K_{bg}}\sum _{i=1}^K(1?b_i)L_{KL}(p_i^{s,T_{bg}},p_i^{t,T_{bg}})\end{array}$$

$L_{KL}(p^{s,T},p^{t,T})=T^2{\sum }_{c=1}^C{p}^{t,T}(c|{\theta }^t)log\frac{p^{t,T}(c|{\theta }^t)}{p^{s,T}(c|{\theta }^s)}$

其中 b i ∈ { 0 , 1 } b_i\in \{0,1\} bi?∈{0,1} 是第 $i$ 个proposal相对于真值目标的二进制标签，${\beta }_{obj}$和${\beta }_{bg}$分别是正样本和负样本的系数，$K_{obj}={\sum }_i{b}_i,K_{bg}={\sum }_i(1?b_i)$ 分别是正样本和负样本的数目

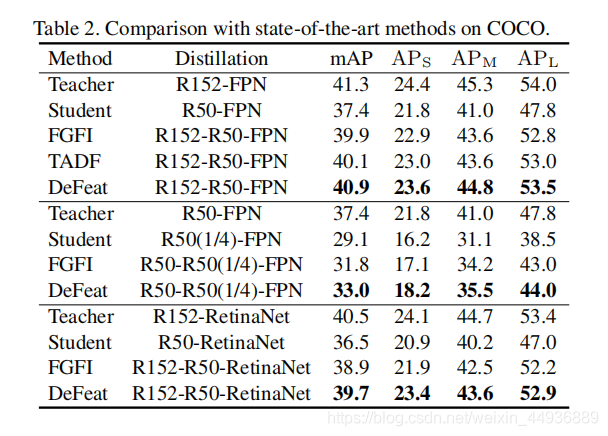
实验结果：

联系作者：

微信号：Sharpiless

作者的其他主页：

B站：https://space.bilibili.com/470550823

CSDN：https://blog.csdn.net/weixin_44936889

AI Studio：https://aistudio.baidu.com/aistudio/personalcenter/thirdview/67156

Github：https://github.com/Sharpiless

我的公众号：