CNN
Why CNN for Image
FNN 处理图片的缺点
- 需要很多的参数假设有一张尺寸100×100的图片(尺寸已经算很小了),那输入层就有100×100×3=30K个像素,假设第一个隐藏层有1K个神经元(一个神经元包含30K个参数),这就已经需要30M个参数了……
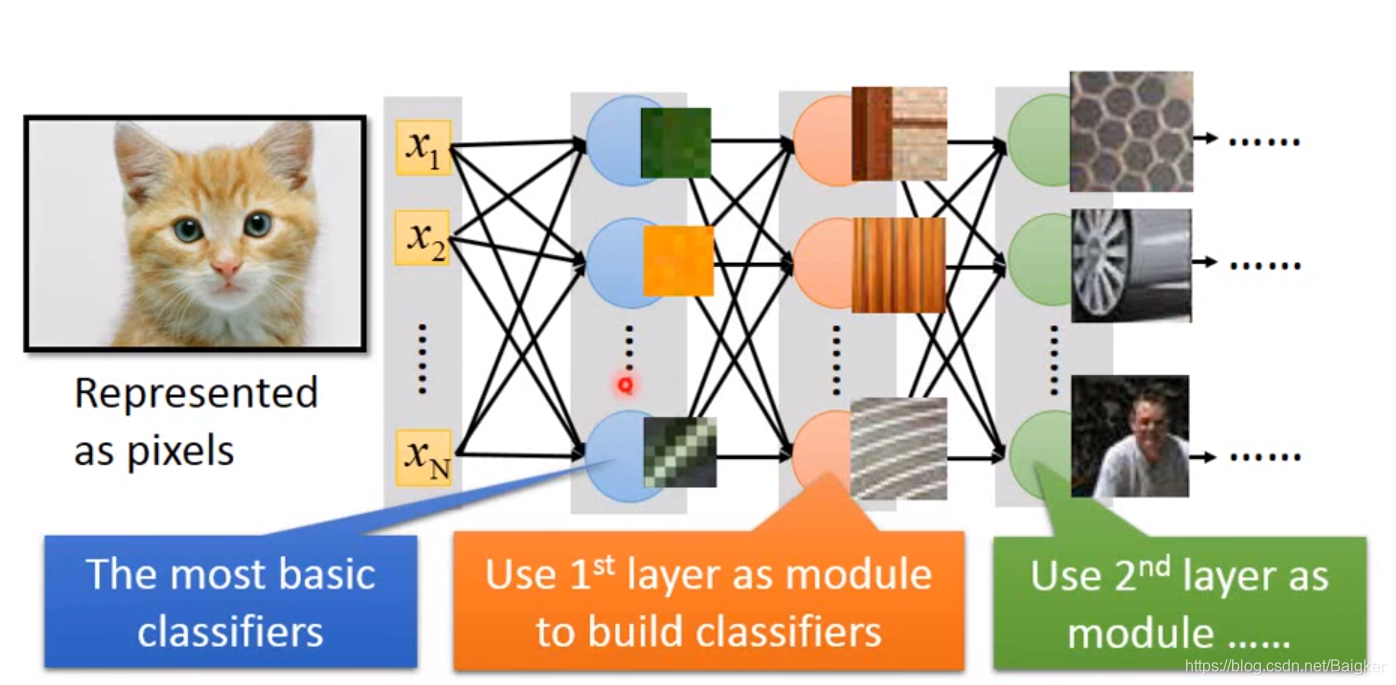
- 该架构中每个神经元就是一个分类器,这是没必要的第一个隐藏层作为最基础的pattern分类器(比如判断有无绿色、边缘等),第二个隐藏层基于第一个隐藏层继续做pattern分类(比如木头、肉类),以此类推……
图片的一些性质
- Some patterns are much smaller than the whole image.

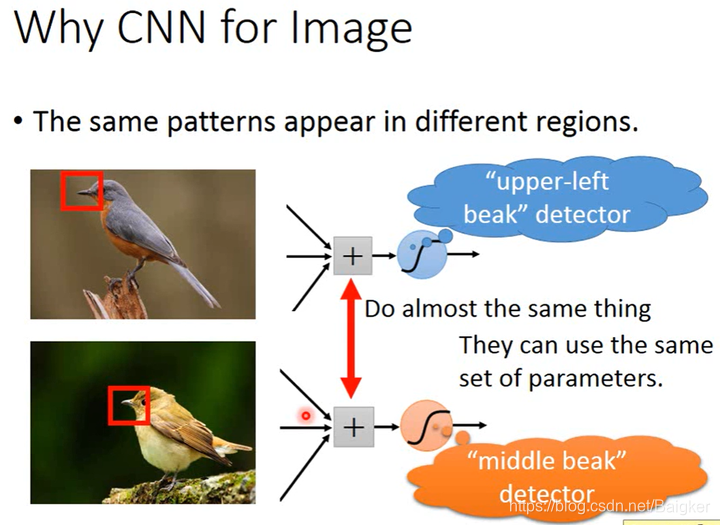
- The same patterns appear in different regions.
3.Subsampling the pixels will not change the object.

CNN架构
CNN可以总结为:多次的Convolution和Max Pooling,然后再用一个Flatten,将结果放入FNN中。、
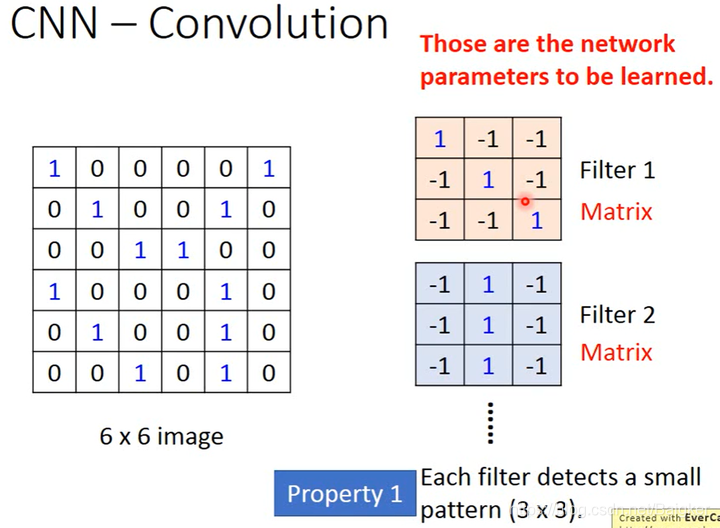
Convolution
假设Image是一个
6
×
6
6 \times 6
6×6的矩阵,值由输入获得。定义Filter(卷积核)是对应的一个神经元。在这里,一个Filter是一个
3
×
3
3 \times 3
3×3的矩阵,值由学习得到。
随后,将Filter和Image的每个
3
×
3
3 \times 3
3×3的子矩阵做内积,得到的值又构成了一个
4
×
4
4 \times 4
4×4矩阵,称为特征图(Feature Map)。
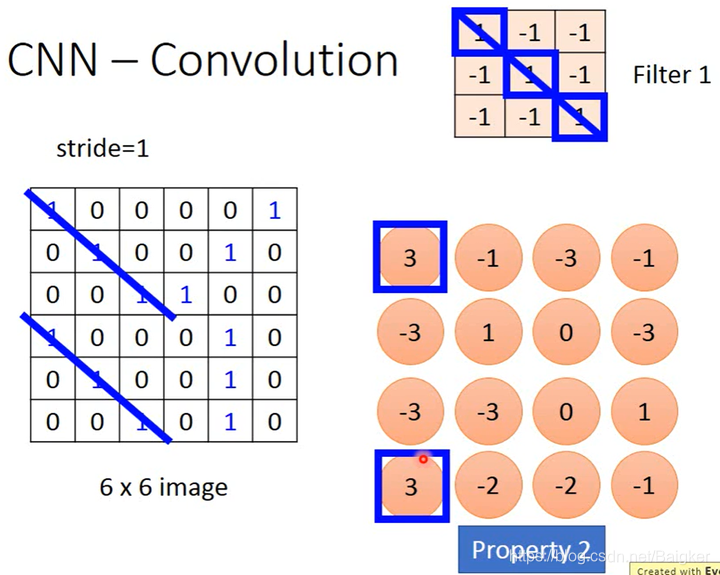
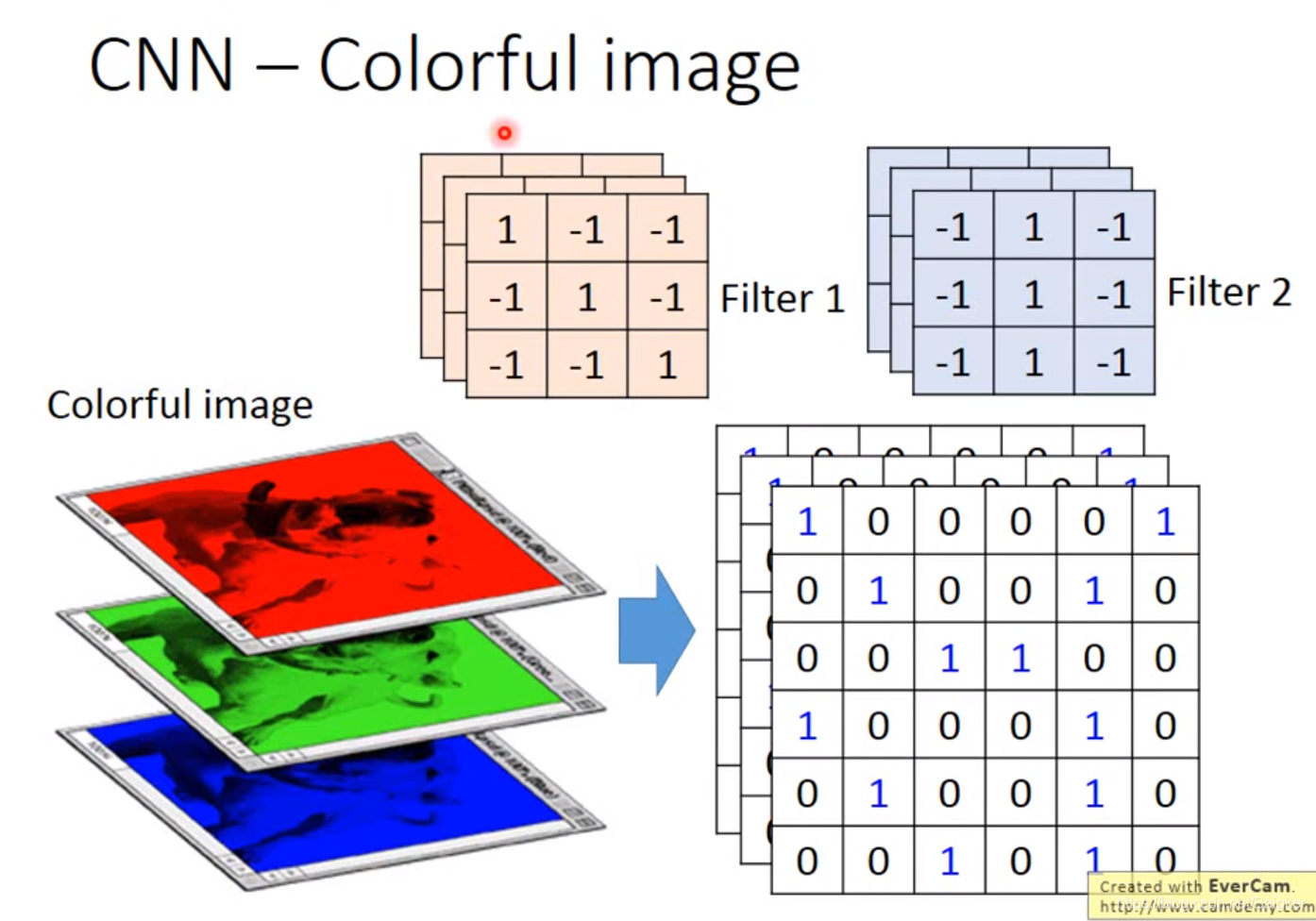
同样的,在处理彩色图片的时候,一个颜色有三个数值表示,就相当于Image是一个三维矩阵,则Filter也要是三维的。
Convolution VS Fully Connected
Convolution 无疑比Fully Connected更有优势,主要有两个优点。
- Convolution 模型的参数更少
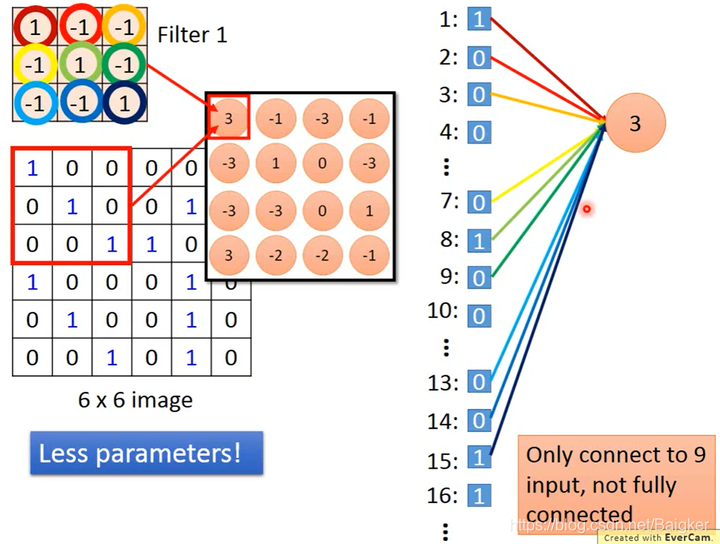
- Convolution 可以在不同区域做卷积时共享参数
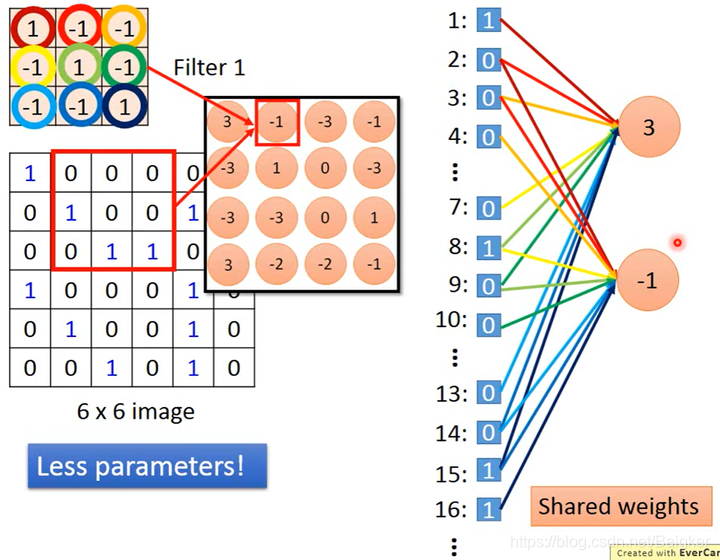
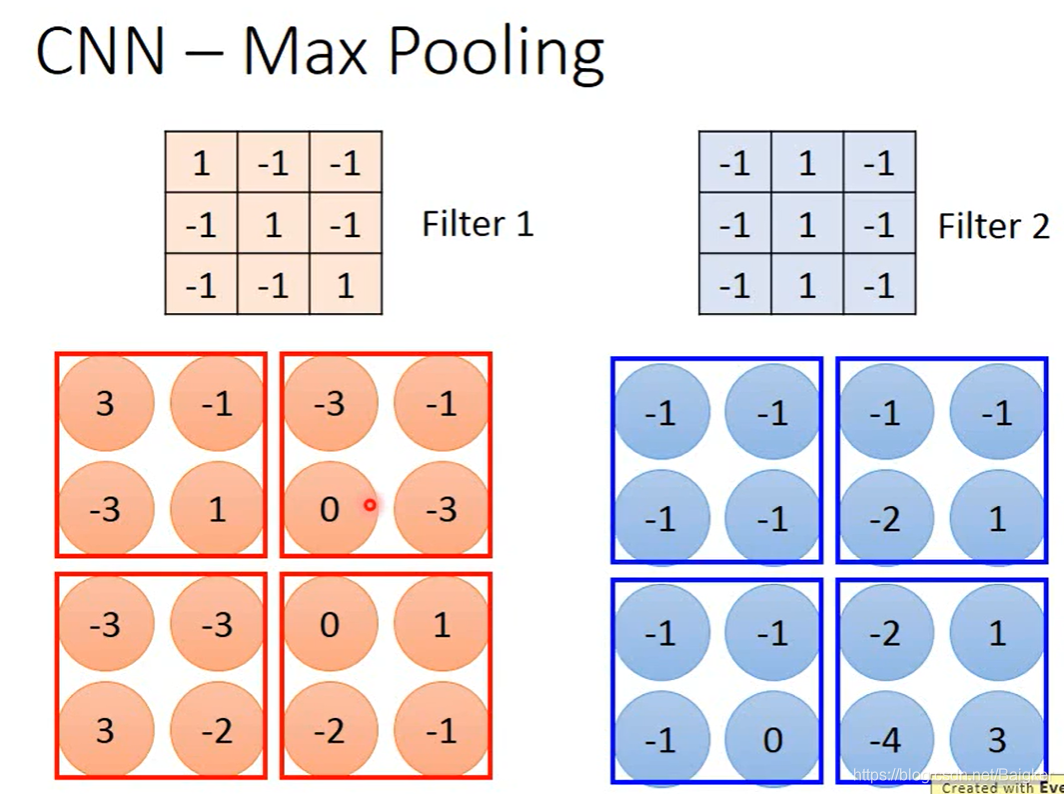
Max Pooling
在Convolution 之后,对得到的矩阵(如本例中的
4
×
4
4 \times 4
4×4的矩阵)进行划分,对每个区域取一个最大值,再次组成一个矩阵。
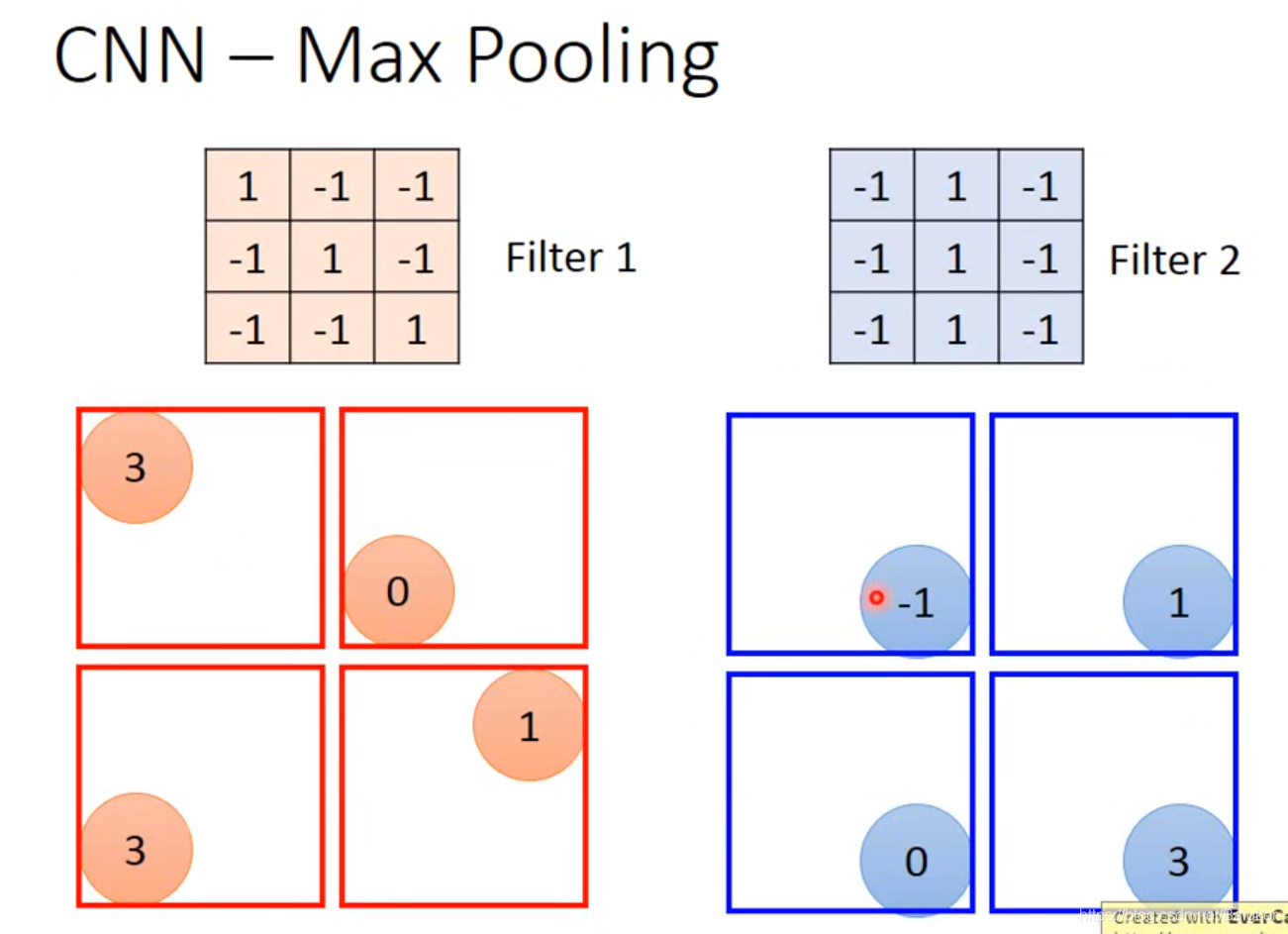
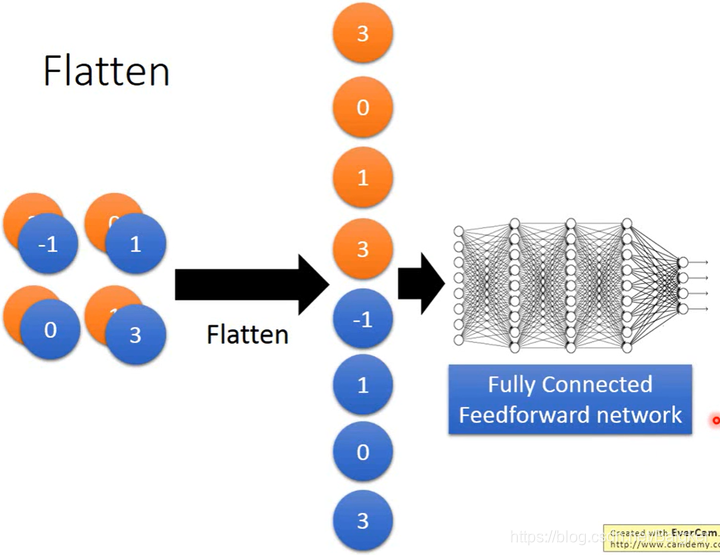
Flatten
经过一系列的Convolution和Max Pooling,将得到的特征图展开排列,作为FNN的输入,最后输出结果。