Backpropagation解决的是在神经网络中如何有效率的进行Gradient?Descent算法的问题。更具体地说,假设将Loss?Function记为,其中
为一个向量,表示所有的参数,那么
的梯度表示为
Backpropagation就是快速计算的一种方法。
定义函数为第n个预测值与真实值之间的距离函数,则Loss?Function可以表示为
将中的某一个参数记为w,
简记为C,下面开始展示
的计算过程。
如图所示是一个神经元,输入为和
,令sigmoid函数的输入
,则根据链式法则,
.
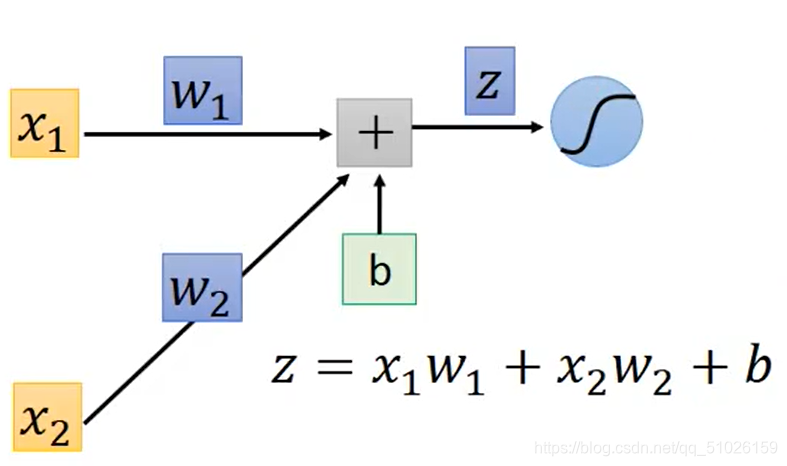
?其中是容易得到的。若
,则
;若
,则
;否则
。但是,计算
需要考虑后面的运算对C带来的影响。
进一步地,令,我们可以得到
??。同样的,
可以由sigmoid函数求导得到,计算
需要考虑后面的运算对C带来的影响。
于是我们考虑下一层神经元。假设这个神经元只与下一层的两个神经元的连接。在下一层中,经过同样的运算可以得到和
。于是
。
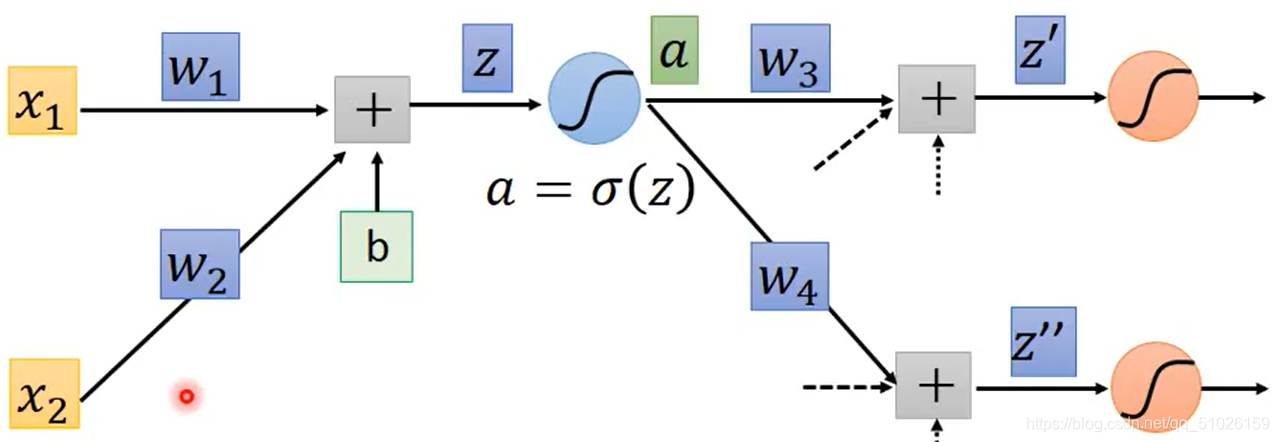
?
?观察这个式子,从图中易得,
,而
和
的求法与
没有任何区别。于是我们考虑:能不能用递推的方法求出所有的
呢?
答案是肯定的。通过以上的推导可以得到递推式
?如果这层神经元不是最后一层,即不是output?layer,则用递推式计算;如果是output?layer,假设输出分别为和
,则
,
。
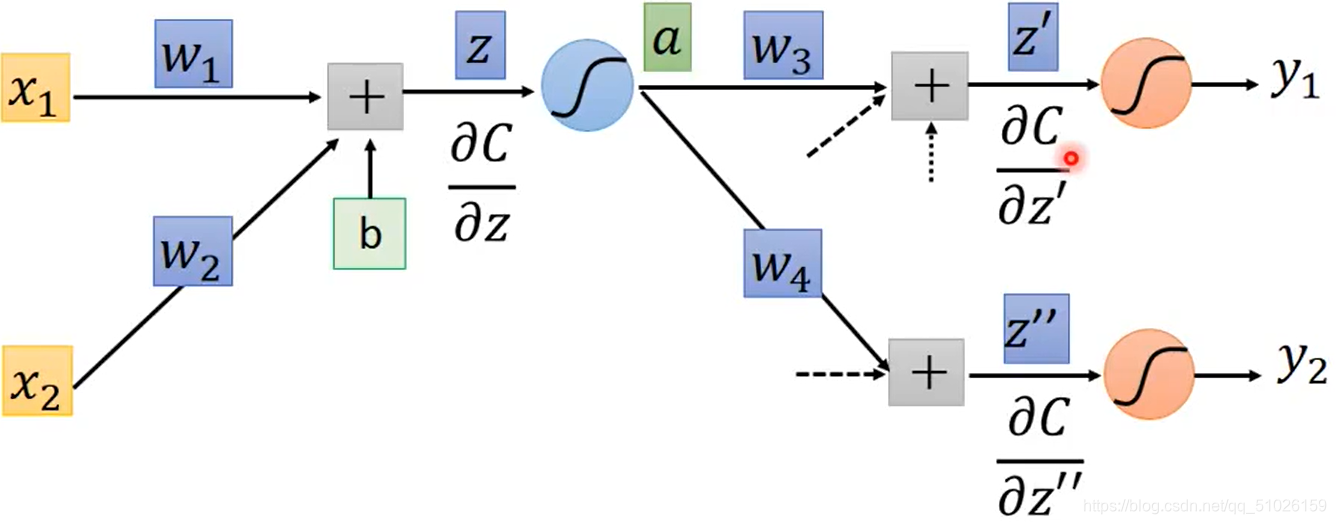
?由于C是距离函数,表达式已知且显含y,所以易于求得。
与此同时,我们观察到,递推式的项数与该神经元连接到的神经元的个数相同,并且同样乘以一个系数之后相加,这个过程与神经网络做的事情很像。于是我们用一个反向的神经元来表示这个计算过程。但是激活函数由sigmoid函数换为乘一个常数,并且没有bias项。
 ?
?
由于这个过程与正常的神经网络进行运算的方向是相反的,所以这个过程又叫做Backward?pass。
整理一遍整个运算过程,假设下图为我们要计算的神经网络。
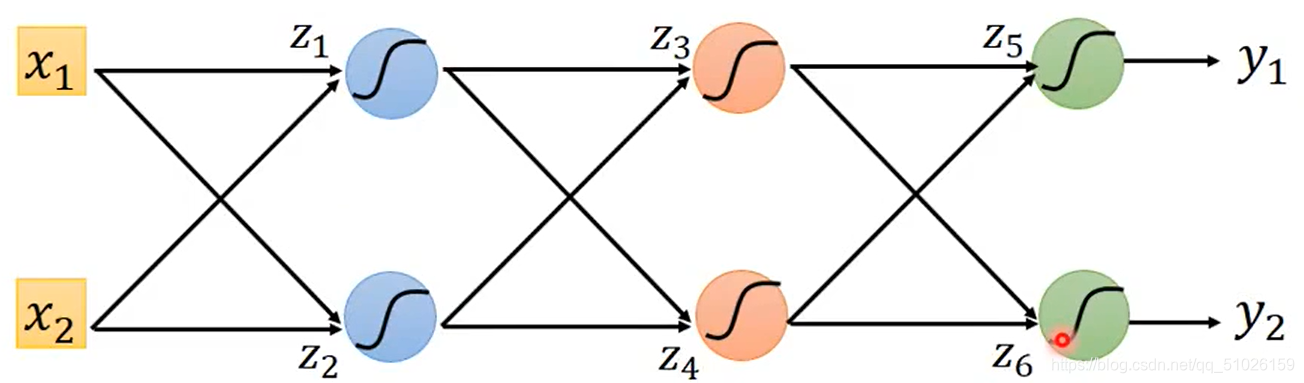
?首先,对整个神经网络进行一次运算,计算出z1,z2…以及y1和y2。
然后进行backward?pass,计算,
…一次性计算出所有需要用到的偏微分值。
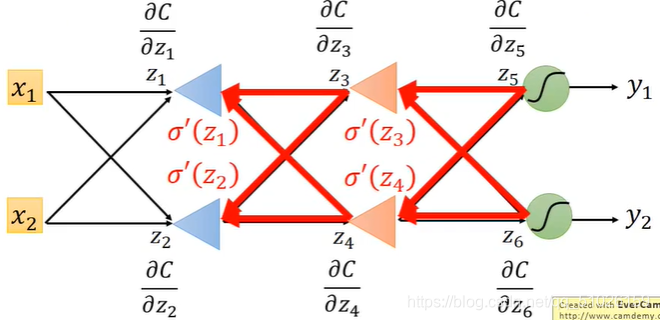
?最后依次对所有参数进行运算即可。
?
?
?
?
?
?
?
?
?
?