[人工智能]Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles

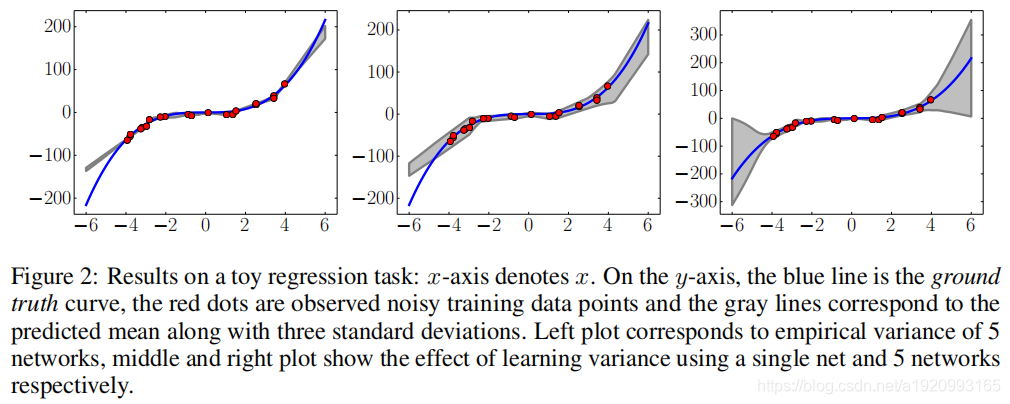
使用深度神经网络集合预测点的分布

1.摘要

深度神经网络是一个在处理黑盒优化问题时的很好的预测器。然而量化神经网络的不确定性的问题仍然具有挑战且有待解决。
贝叶斯神经网络是目前最先进的估计预测不确定性的方法，然而这些方法都需要对训练过程进行重大修改，与标准（非贝叶斯）神经网络相比计算昂贵。
我们提出了一种贝叶斯神经网络的替代方案，它易于实现，易于并行，并产生高质量的预测不确定性估计。通过分类的一系列回归基准实验，我们证明了我们的方法产生了良好校准的不确定性估计，这些估计与近似贝叶斯神经网络一样好或更好。
最后，我们评估了已知和未知类的测试示例的预测不确定性，并表明我们的方法能够在未知类上表达更高程度的不确定性，不像现有的方法即使在未知类上也做出过自信的预测。
本文实现代码：https://github.com/mpritzkoleit/deepensembles/blob/master/Deep%20Ensembles.ipynb
https://github.com/hayoung-kim/tf2-deep-ensemble-uncertainty/blob/master/ensemble.ipynb
https://github.com/muupan/deep-ensemble-uncertainty/blob/master/train_ensemble.ipynb

2.介绍

尽管在监督学习问题中存在令人印象深刻的分类精度和均方误差，但神经网络在量化预测不确定性方面却很差，而且往往对其预测过于自信。评估预测不确定性的质量是具有挑战性的，因为数据的真实条件概率通常是不可用的。
本文主要关注神经网络预测不确定性质量的两种措施。

1. 检查校准情况。校准是主观预测和长期运行的经验预测之间的差异
2. 考虑模型在新数据集上的不确定性

本文贡献如下：

1. 提供了一种简单，可伸缩的方法用于评估神经网络的不确定性，并证明了两种简单的训练途径①集合法②对抗式训练法可以很好校准不确定性的评估
2. 提出了多个测试案例测试不确定性的评估性能。

3.方法

对于分类问题，数据集的标签是K个类别，对于回归问题，数据集的标签是真实值。
本文建议的3种改进法：

1. 合适的评分函数
2. 使用对抗式训练平滑预测分布
3. 训练一个网络集合

3.1合适的评分规则

评分规则用于衡量预测不确定性的质量。它的用处是给一个预测分布函数一个的值，直白点说就是给你的预测网络给出的分布$p_{\theta }(y|x)$打分。我们认为分越高越好。
一个评分规则的数学定义如下：

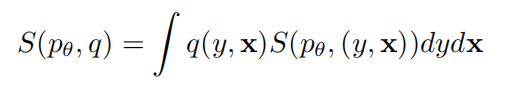
其中$q(y,x)$代表真实(x,y)数据的分布，后面一项是对每个(x,y)的积分。
一个好的评分规则是只有在预测分布$p_{\theta }(x,y)$等于真实分布$q(x,y)$时才会有$S(p_{\theta },q)\ge S(q,q)$发生,即分更高。
有了S后，我们就可以最小化下式的损失函数来得到更好的神经网络。

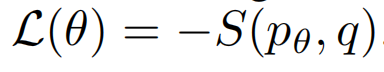
一般来说，普通的神经网络损失函数就是比较合适的评分函数。例如，平方误差MES，最大拟然函数log等。

3.2对抗式训练
首先，我们需要生成对抗式训练用的对抗式数据集。
一般来说，给定一个输入x和目标值y，以及一个损失函数$l(\theta ,x,y)$，一个快速生成一个对抗式数据集例子是：

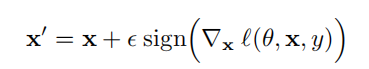
其中，$?$是一个很小的值，使得扰动的最大程度是有限制的。
直观地说，对抗式扰动通过在网络可能增加损失值的方向上加了一个扰动。
假设$?$足够小，这些新的$x^{\prime }$对抗式训练例子可以大大增加数据集。

相比上诉例子对抗式训练，本文提出一个新的视角，考虑下面这个评分规则：

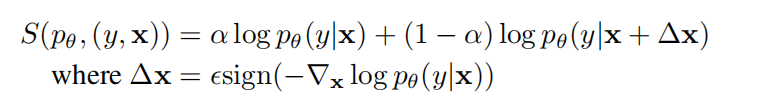
其中，$\alpha$在通常的最大似然分数和对抗性分数之间进行权衡。
如果，$\alpha =1$，我们就只有前一项，此时上诉评分函数变成了一个普通损失函数。如果，$\alpha \le 1$我们可以利用后一项添加的扰动，来更好校准不确定性。简单地说，通过在x旁增加对抗式训练，我们可以平滑网络地预测分布。
一般来说我们希望能在x的所有周围都增加这种对抗式训练，来平滑预测分布，然而这个计算代价太过昂贵。这时候我们会选择loss值很高的一个方向上去进行对抗式训练，细节参考（ Distributional smoothing by virtual
adversarial examples.）。

3.2.1回归问题的训练
通常，在回归问题中我们会使用MES来当loss函数。然而，MES只提供了均值$\mu$，没有捕捉不确定性$\sigma$。
因此，本文的做法是输出两个值，一个是均值$\mu (x)$，一个是方差${\sigma }^2(x)$
我们最小化下面这个log函数：

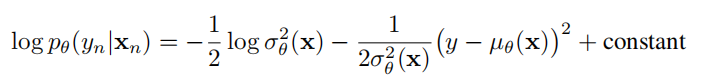
3.3神经网络集的训练
本文对每个神经网络都使用所有数据集。算法流程如下：

最后分布由多个网络平均加权得到：

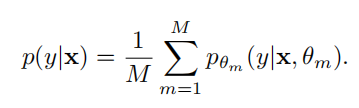
4.实验