目录
1.bp算法介绍
1.1 背景
以人脑中的神经网络为启发,用计算机模拟人脑的神经网络实现类人工智能的机器学习技术,bp算法是至今为止最成功的神经网络算法,bp算法可用于多层向前神经网络
1.2 多层前馈神经网络(Multilayer Feed-Forward Neural Network)
多层前馈神经网络每层神经元与下一层全互连,神经元之间不存在同层连接,也不存在跨层连接
多层前馈神经网络由以下部分组成:
输入层(input layer), 隐藏层 (hidden layers), 输入层 (output layers)
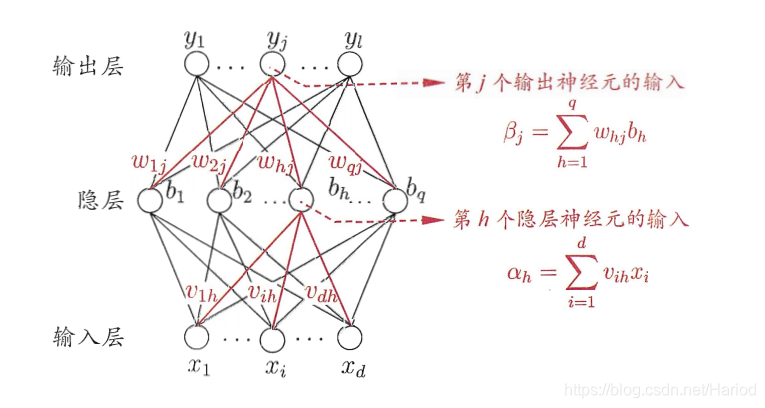
神经网络介绍:
- 每层由神经元组成
- 输入层(input layer)是由训练集的实例特征向量传入
- 经过连接结点的权重(weight)传入下一层,一层的输出是下一层的输入
- 每一神经元输入的值由上一层与其连接的所有神经元的输出与对应权重的累计和,每一层的输出值为累计和加上阈值再根据方程转化得到的值
- 隐藏层的个数可以是任意的,输入层有一层,输出层有一层
- 输出层不算神经网络的层数,隐藏层有任意多个,所有神经网络可以模拟任何计算方程
1.3 神经网络结构的设计
神经网络大多数情况下被用于解决分类问题,使用神经网络训练数据之前,必须确定神经网络的层数,以及每层神经元的个数。在数据集被传入输入层时为了加速神经网络的学习过程通常将数据标准化到0-1之间
输入层神经元数的确定:
由数据集数据种类确定,输入层的神经元数量通常等于类别的数量,比如西瓜色泽A可能取三个值乌黑,青绿,浅白,那么变可以设定输入层神经元数为3,如果输入数据为乌黑(A=乌黑),那么代表乌黑色的神经元就取1,其他两个神经元取0
输出层神经元数的确定:
对于分类问题,如果是2类,可以用一个输出单元表示(0和1分别代表2类)如果多余2类,每一个类别用一个输出单元表示
隐藏层神经元数的确定:
没有明确的规则来设计最好有多少个隐藏层,根据实验测试和误差,以及准确度来实验并改进
1.4 bp算法过程
总的来看bp算法主要通过迭代来处理训练集中的实例,主要步骤为正方向更新每一层神经元的值,然后对比神经网络预测值(输出层值)与真实值之间的误差再反方向以最小化误差更新每个连接的权重与每个神经元的阈值
算法介绍

1.4.1 初始化
初始化权重(weights)和阈值
1.4.2 正向更新神经元值
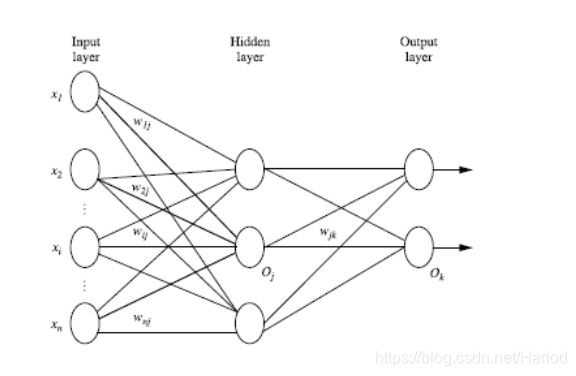
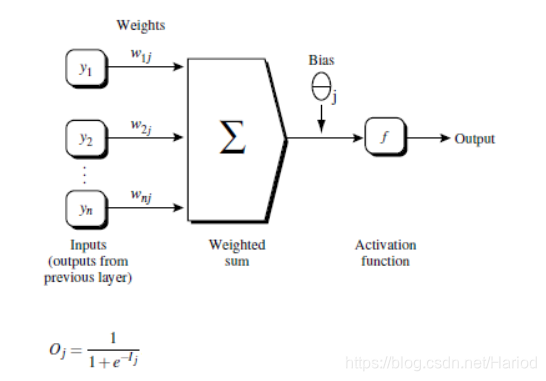
步骤:
- 将训练数据的每个实例赋到输入层
- 隐藏层神经元的输入值为输入层的值与对应的权重累计求和
- 隐藏层神经元将输入值与阈值求和经过函数转化再输出即得到输出值
- 输出层神经元的输入值为隐藏层输出值与对应的权重累计求和
- 输出层神经元将输入值与阈值求和经过函数转化再输出即得到输出值
1.4.3 反向更新权重与阈值
根据输出层值与真实值之间的差反向更新权重与阈值从输出层开始计算到输入层
步骤:
-
输出层误差:
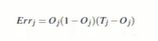
即输出层误差=预测值*(1-预测值)*(真实值-预测值) -
隐藏层误差:
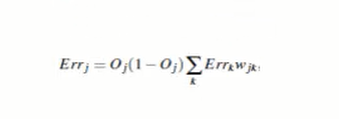
即隐藏层误差=该层输出*(1-该层输出)(下一层误差对应权重累计和) -
权重更新:
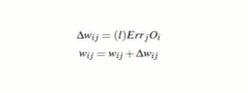
即权重=当前权重+学习率下一层误差当前层输出 -
阈值更新:
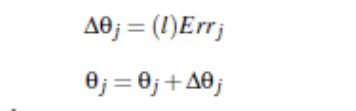
即偏向=当前偏向+学习率*当前层误差 -
输出层神经元将输入值与阈值求和经过函数转化再输出即得到输出值
1.4.4 算法停止
算法停止条件可以根据实际模型训练情况来确定,通常情况下停止条件有以下三种
- 权重的更新低于某个阈值
- 预测的错误率低于某个阈值
- 达到预设一定的循环次数
1.5 bp算法举例
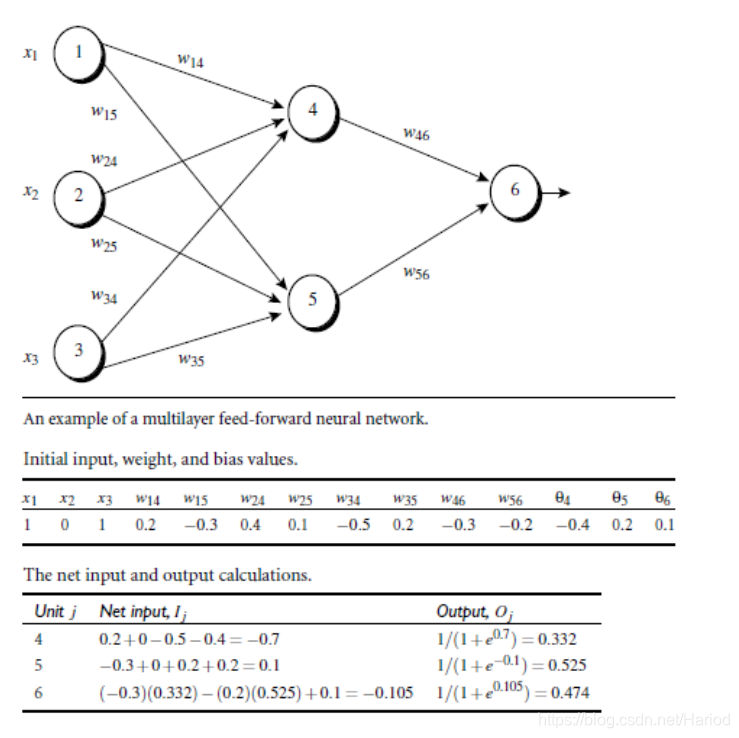

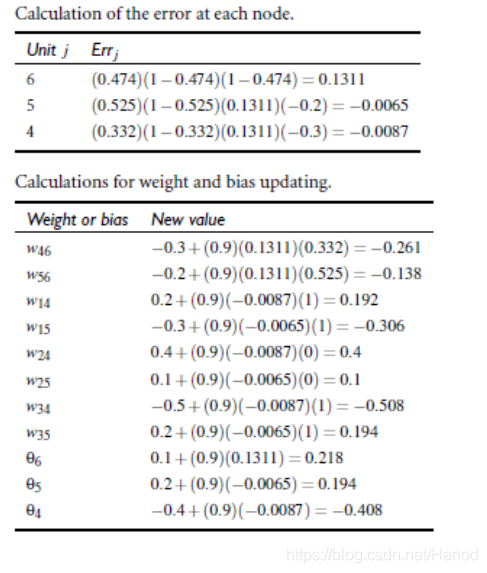
2.bp算法理论推导
本节以周志华西瓜书第五章神经网络里的内容与公式作为基础与参考进行理论推导
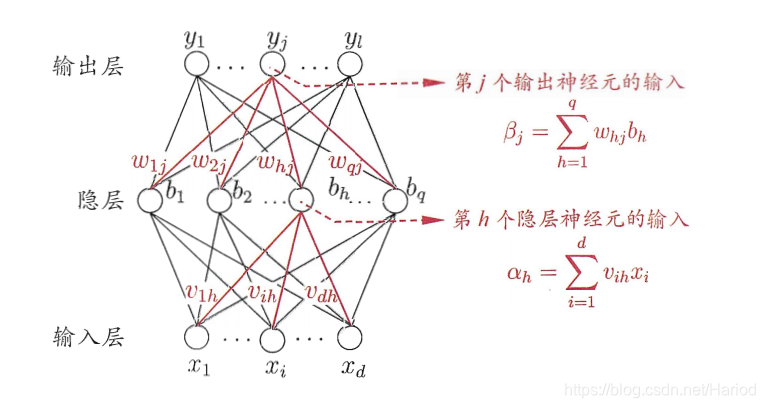

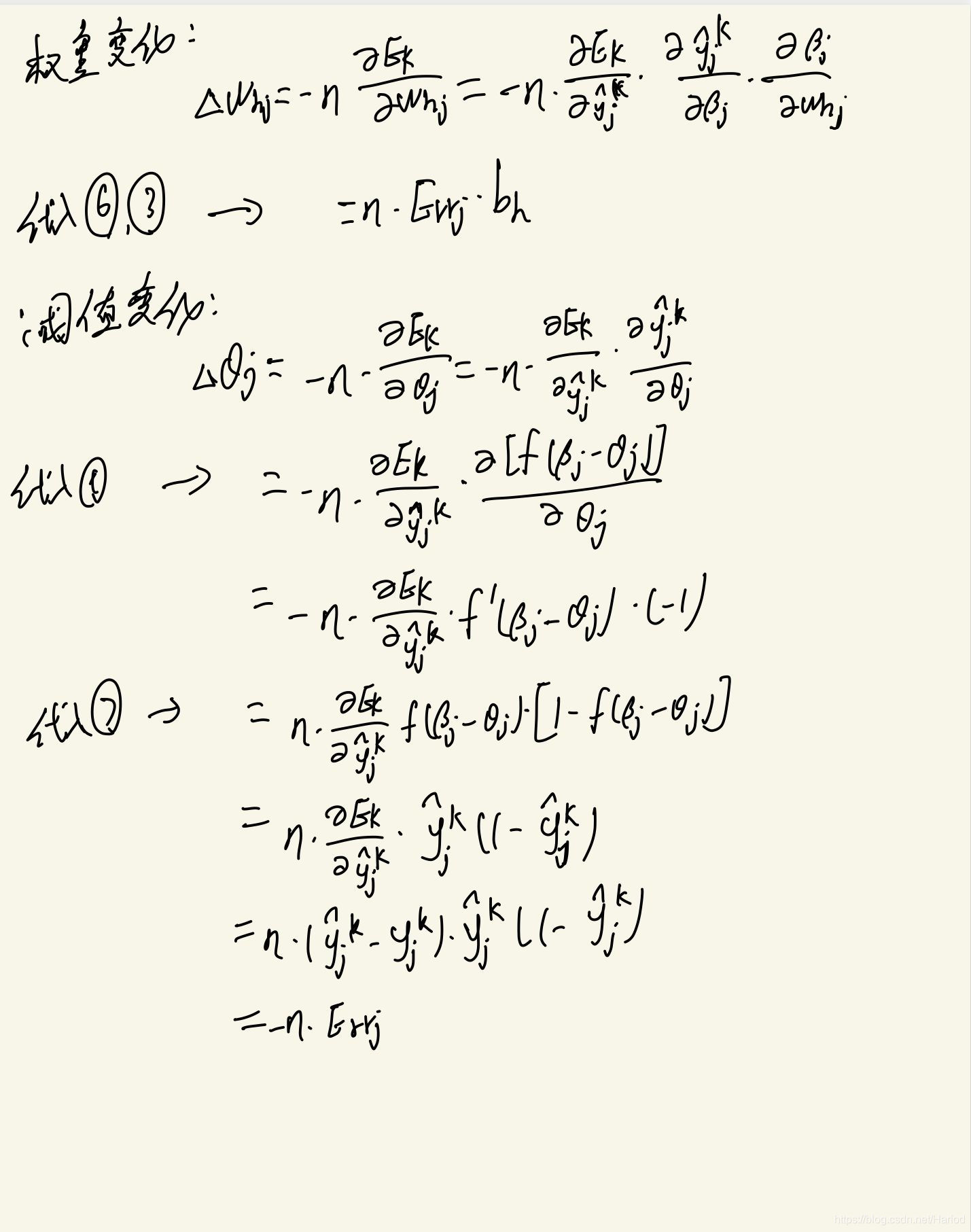
3.bp算法代码举例
下面我们来一个很常规的神经网络例子,用神经网络实现预测异或运算的值,训练集为
[
([0 0],0)
([0 1],1)
([1 0],1)
([1 1],0)
]
import numpy as np
#定义双曲函数
def tanh(x):
return np.tanh(x)
#双曲函数导函数
def tanh_deriv(x):
return 1.0 - np.tanh(x) * np.tanh(x)
#定义逻辑函数
def logistic(x):
return 1 / (1 + np.exp(-x))
#定义逻辑函数导函数
def logistic_derivative(x):
return logistic(x) * (1 - logistic(x))
class NeuralNetwork:
def __init__(self, layers, activation='logistic'):
if activation == 'logistic':
self.activation = logistic#self.activation为逻辑函数
self.activation_deriv = logistic_derivative
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tanh_deriv
self.weights = []#定义权重
for i in range(1, len(layers) - 1):#权重初始化随机赋值
self.weights.append((2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1) * 0.25)
self.weights.append((2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1) * 0.25)
print(self.weights)
def fit(self, X, y, learning_rate=0.2, epochs=10000):
'''
X:输入的数据
y:预测标记
learning_rate:学习率
epochs:设置算法执行次数
'''
X = np.atleast_2d(X) # 转为一个m*n的矩阵
print("输入数据集\n",X)
temp = np.ones([X.shape[0], X.shape[1] + 1]) #初始化一个m*(n+1)的矩阵 X.shape=(4,2)
print("初始化矩阵m*n\n",temp)
temp[:, 0:-1] = X # 偏量的赋值
X = temp
print("偏量\n",X)
y = np.array(y)
print(np.random.randint(X.shape[0]))
for k in range(epochs):
i = np.random.randint(X.shape[0]) #从0到第m-1行随机取一个数
a = [X[i]] #把该行赋值给i
for l in range(len(self.weights)): # 正向更新每个神经元的值
sum_weights=np.dot(a[l], self.weights[l])
a.append(self.activation(sum_weights))
error = y[i] - a[-1] #真实值与预测值的差
deltas = [error * self.activation_deriv(a[-1])] # 计算输出层的误差 对应于输出层计算式
# Staring backprobagation
for l in range(len(a) - 2, 0, -1): # we need to begin at the second to last layer
# Compute the updated error (i,e, deltas) for each node going from top layer to input layer
deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l])) #计算隐藏层误差 对应于隐藏层计算式
deltas.reverse()
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i]) #
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta) #权重更新计算式
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0] + 1)
temp[0:-1] = x
a = temp
for l in range(0, len(self.weights)):
a = self.activation(np.dot(a, self.weights[l]))
return a
nn=NeuralNetwork([2,2,1],'tanh')
x=np.array([[0,0],[0,1],[1,0],[1,1]])
y=np.array([0,1,1,0])
nn.fit(x,y)
for index,data in enumerate([[0,0],[0,1],[1,0],[1,1]]):
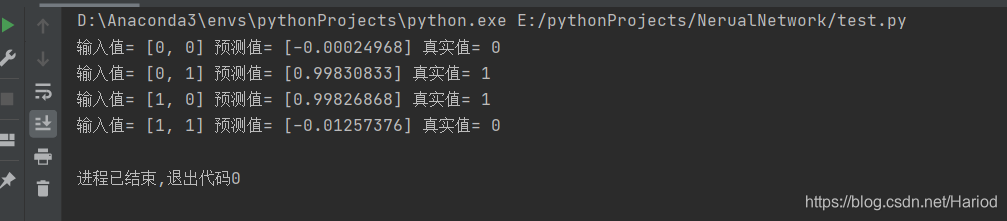
print("输入值=",data,"预测值=",nn.predict(data),"真实值=",y[index])
运行结果如下: