[人工智能]吴恩达：卷积神经网络（Convolutional Neural Networks）

1.1 计算机视觉

1.2 边缘检测示例

卷积的乘法（对应元素相乘，不同于矩阵乘法）fliter过滤器
$$?\begin{array}{cccccc}3& 0& 1& 2& 7& 4\\ 1& 5& 8& 9& 3& 1\\ 2& 7& 2& 5& 1& 3\\ 0& 1& 3& 1& 7& 8\\ 4& 2& 1& 6& 2& 8\\ 2& 4& 5& 2& 3& 9\end{array}???\begin{array}{ccc}1& 0& ?1\\ 1& 0& ?1\\ 1& 0& ?1\end{array}?=?\begin{array}{cccc}?5& ?4& 0& 8\\ ?10& ?2& 2& 3\\ 0& 01& ?4& ?7\\ ?3& ?2& ?3& ?16\end{array}?$$

1.3 更多的边缘检测内容

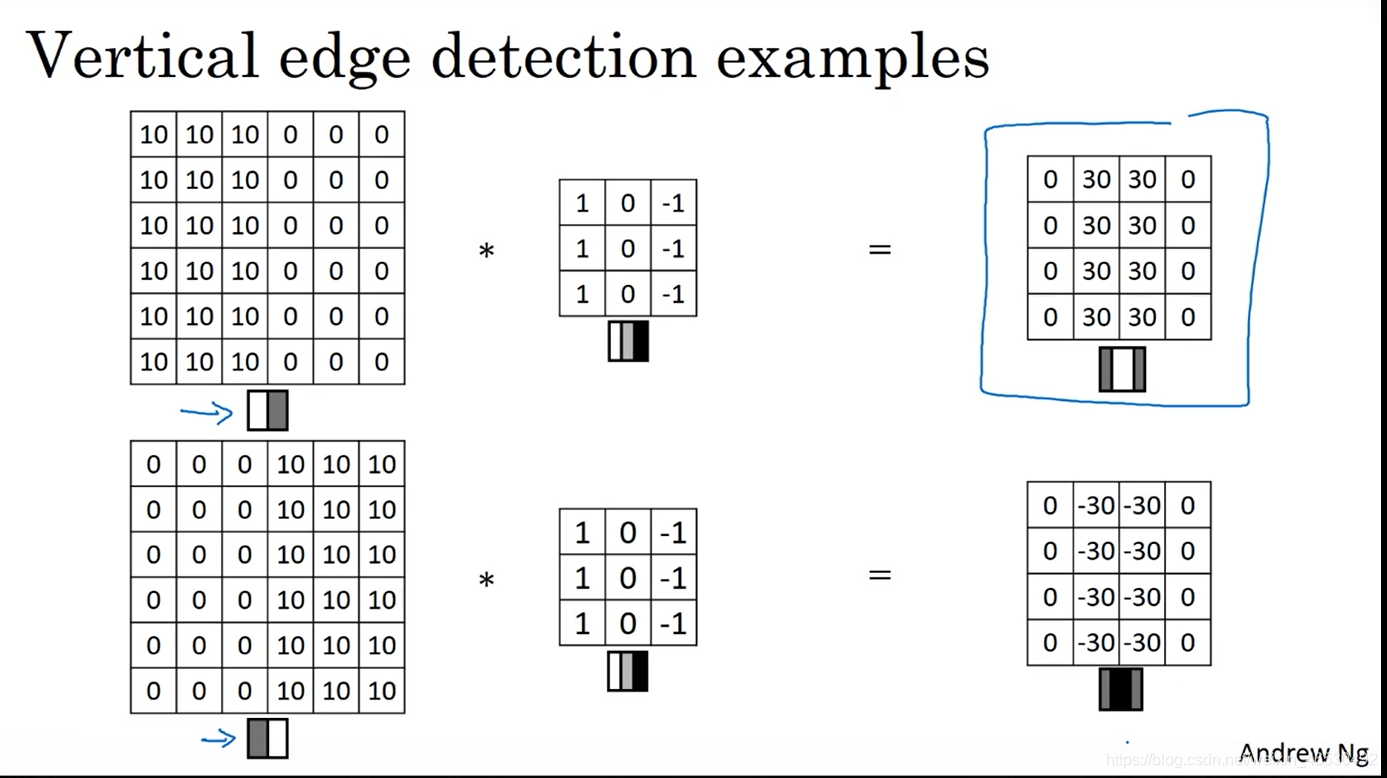
$$\begin{gathered} ?\begin{array}{ccc}1& 0& ?1\\ 1& 0& ?1\\ 1& 0& ?1\end{array}??\begin{array}{ccc}1& 1& 1\\ 0& 0& 0\\ ?1& ?1& ?1\end{array}? \\ verticalhorizontal \\ ?\begin{array}{ccc}1& 0& ?1\\ 2& 0& ?2\\ 1& 0& ?1\end{array}??\begin{array}{ccc}3& 0& ?3\\ 10& 0& ?10\\ 3& 0& ?3\end{array}? \\ soberfilterscharrfilter \end{gathered}$$
还有将filter过滤器设置成参数，通过反向传播进行学习。

1.4 padding

之前的卷积操作会降低图片的维度，可能会使图片维度越来越低，同时边缘的像素只被过滤器利用一次。

习惯上用0来填充，维度变成（n+2p-f+1)*(n+2p-f+1)

valid convolutions:no padding

same convolutions: padding so that output size is the same as the input size.
$$\begin{gathered} （n+2p?f+1)\times (n+2p?f+1) \\ ifn+2p?f+1=n \\ p=\frac{f?1}{2} \end{gathered}$$
所以f一般为奇数，此时首先能保证p是整数，其次奇数的卷积核（kernel）有中心，便于指出过滤器的位置。

1.5 卷积步长 strided convolution

$$\begin{gathered} n\times nimagef\times ffilter \\ paddingpstrides \\ └\frac{n+2p?f}{s}+1┘\times └\frac{n+2p?f}{s}+1┘ \end{gathered}$$

1.6 三维卷积

通过设置立体过滤器（卷积核）的不同通道的数值，可以提取不同层的特征。
$$summary:(n\times n\times n_c)?(f\times f\times n_c)\to (n?f+1)\times (n?f+1)\times n_c^{\prime }$$

1.7 单层神经网络

卷积神经网络：避免过拟合。无论应用到大小图片中，参数数量不变

if you have 10 filters that are 3x3x3 in one layer of a neural network, how many parameters does that layers have?

(3x3x3+1) x 10 = 280

1.8 简单卷积网络示例

卷积核是特征提取器，卷积核越多，提取的信息越多。

Types of layers in a convolutional network?

• Convolution (CONV)
• Pooling (POOL)
• Fully connected (FC)

1.9 池化层

池化层：缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性。

目前来说，最大池化比平均池化更常用，但也有例外，就是深度很深的神经网络。

summary of pooling

hyperparameters:

f: filter size

s: stride

Max(f=2,s=2) or average(f=3,s=2) pooling

1.10 卷积神经网络示例

随着层数的增加，高度和宽度都会减小，而通道数量会增加。

1.11 为什么使用卷积？

卷积神经网络可以用两种方式减少参数，以便于我们用更小的训练集训练它，从而预防过度拟合。

为什么使用卷积：参数共享和稀疏连接

2.1 为什么要进行实例研究？

classic networks:LeNet-5、AlexNet、VGG

ResNet、Inception.

2.2 经典网络

2.3 残差网络

skip connect（远跳连接）：$a^{[l]}$跳过一层或好几层，从而将信息传递到神经网络的更深层。

residual network 能够达到网络的更深层，这种方式确实有助于解决梯度消失和梯度爆炸问题。让我们在训练更深网络的同时，又能保证良好的性能。

2.4 残差网络为什么有用？

网络深度越深，它在训练集上训练网络的效率会有所减弱，这也是有时候我们不希望加深网络的原因。

残差网络有用的主要原因是这些残差层学习恒等函数很容易，至少网络性能不会受到影响，很多时候甚至可以提高效率，或者说至少不会降低效率。
$$\begin{gathered} a^{[l+2]}=g(z^{[l+2]}+a^{[l]}) \\ =g(w^{[l+2]}{a}^{[l+1]}+b^{[l+2]}+a^{[l]}) \\ 假设w^{[l+2]}、b^{[l+2]}均为0，则有 \\ =g(a^{[l]})=a^{[l]}(ReLU函数) \end{gathered}$$

2.5 网络中的网络以及1x1卷积

1x1卷积可以在保证高度宽度不变的情况下压缩信道数量并减少计算。

2.6 谷歌inception网络简介

2.7 inception网络

2.8 使用开源的实现方案

2.9 迁移学习

冻结前面所有的层，只把softmax层改动以适应自己的实现。

2.10 数据扩充

mirroring镜像对称、random cropping随机修剪、rotation、shearing、local warping

color shifting(rgb通道)

2.11 计算机视觉现状

3.1 目标定位object localization

Need to output $b_x,b_y,b_h,b_w$,class label (1,-4)

$y=[p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3]$

$L(\hat{y},y)={\sum }_{i=1}^8(\widehat{y_i}?y_i{)}^2$

3.2 特征点检测landmark detection

$ConvNet\to [face,l_{1x},l_{1y},l_{2x},l_{2y},\dots \dots ,l_{64x},l_{64y}]$ 129

3.3 目标检测object detection

3.4 卷积的滑动窗口实现

convolution implementation of sliding windows

3.5 Bounding Box预测

YOLO:you only look once

YOLO计算速度非常快，可以达到实时识别，

3.6 交并化intersection over union（IOU)

Evaluating object localization 交并比函数

计算两个边框交集与并集之比

“correct” if IoU > 0.5

3.7 非极大值抑制Non-max suppression

3.8 Ancher Boxes

ancher boxes:为了处理两个对象出现在同一个格子里的情况，可以使你的训练集更有针对性（很高很瘦的行人和很长很低的车子）
$$\begin{gathered} y=[p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3,p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3] \\ anchorbox1anchorbox2 \end{gathered}$$

3.9 YOLO算法

3.10 候选区域region proposal

R-CNN:带区域的卷积神经网络

首先得到候选区域，然后再分类，所以速度较慢。

4.1 什么是人脸识别？

face verification人脸验证

• input image，name/ID
• output whether the input image is that of the claimed person.

face recognition人脸识别

• has a database of K persons
• get an input image
• output ID if the image is any of the K persons (or “not recognized”)

4.2 One-Shot学习

d(img1,img2) = degree of difference between images

if d(img1,img2) $\le \tau$

4.3 Siamese网络

4.4 Triplet损失(三元组)

Anchor、Positive、Negative
$$\begin{gathered} ||f(A)?f(P)|{|}^2+\alpha \le ||f(A)?f(N)|{|}^2 \\ ||f(A)?f(P)|{|}^2?||f(A)?f(N)|{|}^2+\alpha \le 0 \\ \alpha :margin(间隔) \\ lossfunction:L(A,P,N)=max(||f(A)?f(P)|{|}^2?||f(A)?f(N)|{|}^2+\alpha ,0) \\ J=\sum _{i=1}^{m}L(A^{(i)},P^{(i)},N^{(i)}) \end{gathered}$$

4.5 面部验证和二分类

把人脸验证当做一个监督学习，创建一个成对图片的训练集（不再是三个一组），目标标签是1表示两张图片是同一个人

4.6 什么是神经风格转换？

4.7 什么是深度卷积网络？

4.8 代价函数_bilibili

$J(G)=\alpha J_{content}(C,G)+\beta J_{style}(S,G)$

4.9 内容代价函数

4.10 风格代价函数

$$\begin{gathered} Let{a}_{i,j,k}^{[l]}=activationat(i,j,k).G^{[l]}is{n}_c^{[l]}\times n_c^{[l]} \\ {G}_{k{k}^{\prime }}^{[l](S)}=\sum _{i=1}^{n_H^{[l]}}\sum _{j=1}^{n_W^{[l]}}{a}_{ijk}^{[l](S)}{a}_{ij{k}^{\prime }}^{[l](S)} \\ {G}_{k{k}^{\prime }}^{[l](G)}=\sum _{i=1}^{n_H^{[l]}}\sum _{j=1}^{n_W^{[l]}}{a}_{ijk}^{[l](G)}{a}_{ij{k}^{\prime }}^{[l](G)} \\ {J}_{style}^{[l]}(S,G)=\frac{1}{2n_H^{[l]}{n}_W^{[l}{n}_C^{[l]}}||G_{k{k}^{\prime }}^{[l](S)}?G_{k{k}^{\prime }}^{[l](G)}|{|}_F^2 \\ =\frac{1}{2n_H^{[l]}{n}_W^{[l}{n}_C^{[l]}}\sum _k\sum _{k^{\prime }}(G_{k{k}^{\prime }}^{[l](S)}?G_{k{k}^{\prime }}^{[l](G)}{)}^2 \end{gathered}$$

4.11 一维到三维推广