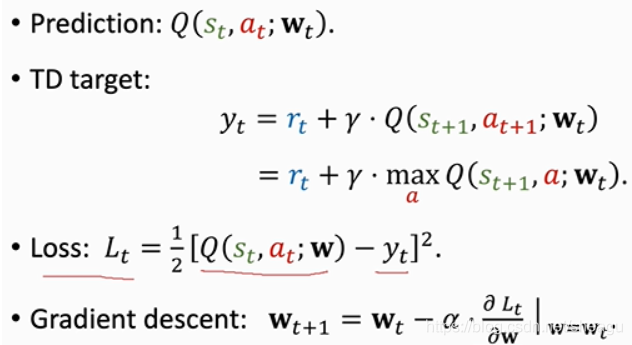[人工智能]强化学习：（二）价值学习

valued-based learnning with Deep Q-Network (DQN)

目标：使reward最大化

a的选择：

1）如果已经知道了 $Q^{?}(s,a)$ ，那么最好的 $a^{?}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}{\mathrm{Q}}^{?}(\mathrm{s},\mathrm{a})$， 也就是使得平均回报值最大的a

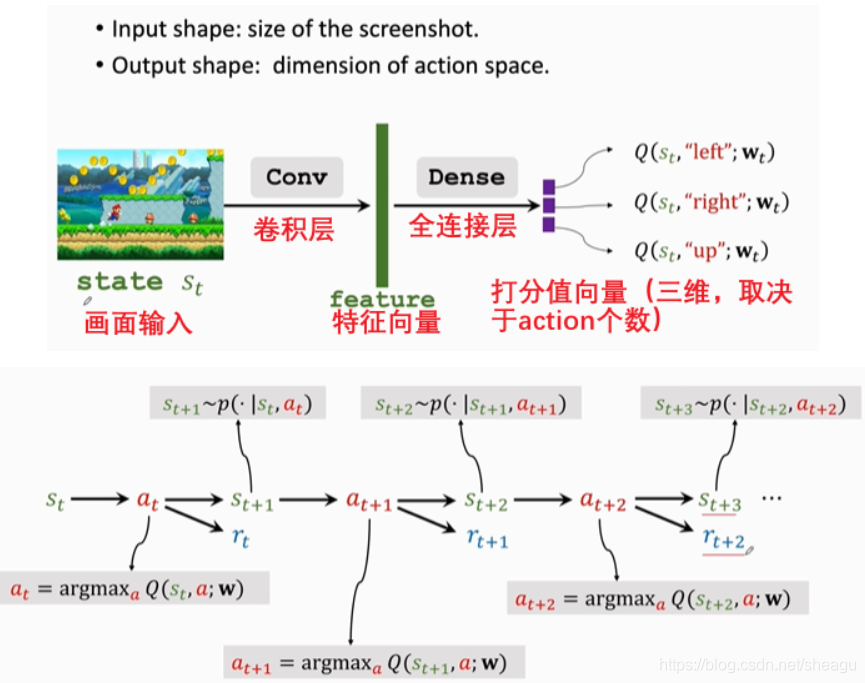
2）其实我们不知道 $Q^{?}(s,a)$ ，我们需要把他学习出来，比如用Deep Q-Network (DQN)。基本思路：用一个神经网络 $Q(s,a;w)$ 来近似出 $Q^{?}(s,a)$ ，其中w是参数，s为输入，输出为一系列打分值，不断提高打分值的合理性，以此优化网络。

一、TD算法

如何训练DQN？TD算法（temporal difference learning，瞬时差分法）最常用

先来看一个例子。一般的参数更新方法：比如我想知道从NYC到atlanta要多久，我先估计是1000min，然后实际开车去一次，测得860min，最后更新估计值。具体的表达式如下：

估计：$q=Q(w)$

真实值：$y$

loss：$L=\frac{1}{2}(q?y{)}^2$

gradient：

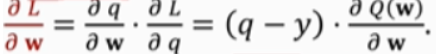
gradient descent（梯度下降）：

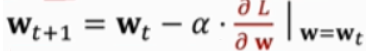
其中 α 称为学习率

缺点：需要完成整个旅途才能对模型做一次更新

利用半路上的数据进行w的优化：先估计是1000min，然后从NYC开到DC，发现用了300min，此时重新估计剩余路程的时间为600min，则从NYC到atlanta的估计为300+600=900，这个900称为TD target，它比原来的1000更准，用y表示（这里y不再是真实值了，因为包含了一段估计，应该理解为“充分利用已知信息得到的最好的值”）。（越接近亚特兰大，TD target越准）

TD error：$Q(w)?y$，注意这不是估计值与真实值的差，而是第一次估计和第二次估计的差

loss：$L=\frac{1}{2}(Q(w)?y{)}^2$

gradient：

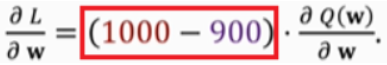
gradient descent（梯度下降）：

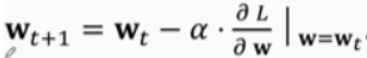
TD算法的目标就是让TD error趋于0（也就是前一次估计和后一次估计一样，说明估计值不能再好了）

TD算法的使用条件：

二、在DRL中使用TD算法

上面的式子是怎么来的呢？先看 $U_t$ 的动态：

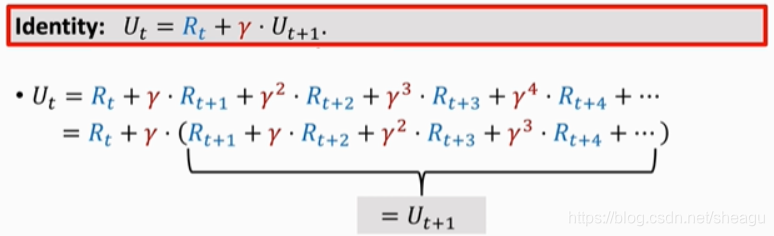
而Q是对U的期望，因此：

它的形式和TD算法的迭代是相同的

用TD算法训练DQN（更新其参数的过程）：

三、参考资料

深度强化学习（全）