开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 集成学习方法二 -> 正文阅读

[人工智能]集成学习方法二

请添加图片描述

bagging：

对不同的子集使用同一种基本模型进行拟合，然后投票得出最终的预测
降低方差

boosting：

使用同一组数据集进行反复学习，得到一系列简单模型，然后组合这些模型构成一个预测性能十分强大的机器学习模型
减小偏差

boosting

基本思路

弱学习：识别错误率小于1/2（即准确率仅比随机猜测略高的学习算法）
强学习：识别准确率很高并能在多项式时间内完成的学习算法

在PAC 学习的框架下，强可学习和弱可学习是等价的

从弱学习算法出发，反复学习，得到一系列弱分类器(又称为基本分类器)，然后通过一定的形式去组合这些弱分类器构成一个强分类器

大多数的Boosting方法都是通过改变训练数据集的概率分布(训练数据不同样本的权值)，针对不同概率分布的数据调用弱分类算法学习一系列的弱分类器

boosting方法要解决的两个问题：

每一轮学习应该如何改变数据的概率分布？
如何将各个弱分类器组合起来？

Adaboost算法

基本原理

提高那些被前一轮分类器错误分类的样本的权重，而降低那些被正确分类的样本的权重

各个弱分类器的组合是通过采取加权多数表决的方式，加大分类错误率低的弱分类器的权重，因为这些分类器能更好地完成分类任务，而减小分类错误率较大的弱分类器的权重，使其在表决中起较小的作用

算法步骤

给定一个二分类的训练数据集： $T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}$ ，其中每个样本点由特征与类别组成。特征 $x_{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}$ ，类别 $y_{i} \in \mathcal{Y}=\{-1,+1\}$ ， $\mathcal{X}$ 是特征空间，$ \mathcal{Y} $是类别集合，输出最终分类器$ G(x)$

(1) 初始化训练数据的分布： $D_{1}=\left(w_{11}, \cdots, w_{1 i}, \cdots, w_{1 N}\right), \quad w_{1 i}=\frac{1}{N}, \quad i=1,2, \cdots, N$ (训练数据的权值分布是均匀分布——为了使得第一次没有先验信息的条件下每个样本在基本分类器的学习中作用一样)

(2) 对于m=1,2,…,M

使用具有权值分布 $D_m$ 的训练数据集进行学习，得到基本分类器： $G_{m}(x): \mathcal{X} \rightarrow\{-1,+1\}$
计算 $G_m(x)$ 在训练集上的分类误差率 $e_{m}=\sum_{i=1}^{N} P\left(G_{m}\left(x_{i}\right) \neq y_{i}\right)=\sum_{i=1}^{N} w_{m i} I\left(G_{m}\left(x_{i}\right) \neq y_{i}\right)$
计算 $G_m(x)$ 的系数** $\alpha_{m}=\frac{1}{2} \log \frac{1-e_{m}}{e_{m}}$ **，这里的log是自然对数ln (表示了 $G_m(x)$ 在最终分类器的重要性程度) ,当 $e_{m} \leqslant \frac{1}{2}$ 时， $\alpha_{m} \geqslant 0$ ，并且 $\alpha_m$ 随着 $e_m$ 的减少而增大，因此分类错误率越小的基本分类器在最终分类器的作用越大
更新训练数据集的权重分布
$\begin{array}{c} D_{m+1}=\left(w_{m+1,1}, \cdots, w_{m+1, i}, \cdots, w_{m+1, N}\right) \\ w_{m+1, i}=\frac{w_{m i}}{Z_{m}} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right), \quad i=1,2, \cdots, N \end{array}$
样本权重的更新为：
$w_{m+1, i}=\left\{\begin{array}{ll} \frac{w_{m i}}{Z_{m}} \mathrm{e}^{-\alpha_{m}}, & G_{m}\left(x_{i}\right)=y_{i} \\ \frac{w_{m i}}{Z_{m}} \mathrm{e}^{\alpha_{m}}, & G_{m}\left(x_{i}\right) \neq y_{i} \end{array}\right.$

这里的 $Z_m$ 是规范化因子，使得 $D_{m+1}$ 称为概率分布， $Z_{m}=\sum_{i=1}^{N} w_{m i} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right)$

可以看出，被基本分类器 $G_m(x)$ 错误分类的样本的权重扩大，被正确分类的样本权重减少，二者相比相差 $\mathrm{e}^{2 \alpha_{m}}=\frac{1-e_{m}}{e_{m}}$ 倍

(3) 构建基本分类器的线性组合 $f(x)=\sum_{m=1}^{M} \alpha_{m} G_{m}(x)$ ——加权表决，得到最终的分类器

$\begin{aligned} G(x) &=\operatorname{sign}(f(x)) \\ &=\operatorname{sign}\left(\sum_{m=1}^{M} \alpha_{m} G_{m}(x)\right) \end{aligned}$

向前分步算法

给定数据集 $T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}$ ， $x_{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}$ ， $y_{i} \in \mathcal{Y}=\{+1,-1\}$ 。损失函数 $L (y, f (x))$ ，基函数集合 $\{b(x ; \gamma)\}$ ，我们需要输出加法模型 $f (x)$ 。

初始化： $f_{0}(x)=0$
对m = 1,2,…,M:
- (a) 极小化损失函数：
  $\left(\beta_{m}, \gamma_{m}\right)=\arg \min _{\beta, \gamma} \sum_{i=1}^{N} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+\beta b\left(x_{i} ; \gamma\right)\right)$
  得到参数 $\beta_{m}$ 与 $\gamma_{m}$
- (b) 更新：
$f_{m}(x)=f_{m-1}(x)+\beta_{m} b\left(x ; \gamma_{m}\right)$
得到加法模型：
$f(x)=f_{M}(x)=\sum_{m=1}^{M} \beta_{m} b\left(x ; \gamma_{m}\right)$

这样，前向分步算法将同时求解从m=1到M的所有参数 $\beta_{m}$ ， $\gamma_{m}$ 的优化问题简化为逐次求解各个 $\beta_{m}$ ， $\gamma_{m}$ 的问题

梯度提升决策树(GBDT)

在回归树中的样本标签是连续数值，可划分点包含了所有特征的所有可取的值。所以再使用熵之类的指标不再合适，取而代之的是平方误差，它能很好的评判拟合程度。

用每个样本的残差表示每次使用基函数预测时没有解决的那部分问题

提升树算法

输入数据集 $T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}, x_{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}, y_{i} \in \mathcal{Y} \subseteq \mathbf{R}$ ，输出最终的提升树 $f_{M}(x)$

初始化 $f_0(x) = 0$
对m = 1,2,…,M：
- 计算每个样本的残差: $r_{m i}=y_{i}-f_{m-1}\left(x_{i}\right), \quad i=1,2, \cdots, N$
- 拟合残差 $r_{mi}$ 学习一棵回归树，得到 $T\left(x ; \Theta_{m}\right)$
- 更新 $f_{m}(x)=f_{m-1}(x)+T\left(x ; \Theta_{m}\right)$
得到最终的回归问题的提升树： $f_{M}(x)=\sum_{m=1}^{M} T\left(x ; \Theta_{m}\right)$

梯度提升算法

梯度提升算法(gradient boosting)，这是利用最速下降法的近似方法，利用损失函数的负梯度在当前模型的值 $-\left[\frac{\partial L\left(y, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)}$ 作为回归问题提升树算法中的残差的近似值，拟合回归树。与其说负梯度作为残差的近似值，不如说残差是负梯度的一种特例。
以下开始具体介绍梯度提升算法：
输入训练数据集 $T=\left\{\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), \cdots,\left(x_{N}, y_{N}\right)\right\}, x_{i} \in \mathcal{X} \subseteq \mathbf{R}^{n}, y_{i} \in \mathcal{Y} \subseteq \mathbf{R}$ 和损失函数 $L (y, f (x))$ ，输出回归树 $\hat{f}(x)$

初始化 $f_{0}(x)=\arg \min _{c} \sum_{i=1}^{N} L\left(y_{i}, c\right)$
对于m=1,2,…,M：
- 对i = 1,2,…,N计算： $r_{m i}=-\left[\frac{\partial L\left(y_{i}, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)}$
- 对 $r_{mi}$ 拟合一个回归树，得到第m棵树的叶结点区域 $R_{m j}, j=1,2, \cdots, J$
- 对j=1,2,…J，计算： $c_{m j}=\arg \min _{c} \sum_{x_{i} \in R_{m j}} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+c\right)$
- 更新 $f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$
得到回归树： $\hat{f}(x)=f_{M}(x)=\sum_{m=1}^{M} \sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$

梯度提升算法讲解

XGboost算法

XGboost算法详解

作业

1.Adaboost的基本思路

Adaboost是在初始化权重都相同的数据集下进行学习得到基本学习器，然后提高错误分类样本的权重，减小正确分类样本的权重，得到新的权重分布，然后循环操作，最后实现对多个基本分类器的加权表决。

2.Adaboost和GBDT的联系与区别

联系：

AdaBoost和Gradient Boosting每次基于先前模型的表现选择一个表现一般的新模型并且进行调整，两者都是基于加法模型和前向分步算法

区别：

AdaBoost是通过提升错分数据点的权重来定位模型的不足

Gradient Boosting是通过算梯度（gradient）来定位模型的不足，Gradient Boosting可以使用更多种类的目标函数,而当目标函数是均方误差时，计算损失函数的负梯度值在当前模型的值即为残差

3.boosting与bagging的区别，以及如何提升模型的精度？

bagging：

对不同的子集使用同一种基本模型进行拟合，然后投票得出最终的预测
降低方差

boosting：

使用同一组数据集进行反复学习，得到一系列简单模型，然后组合这些模型构成一个预测性能十分强大的机器学习模型
减小偏差

4.使用基本分类模型和Boosting提升模型，画出他们的决策边界

使用Adaboost算法根据葡萄酒数据集预测红酒属于哪一个类别

加载数据

# 引入数据科学相关工具包：
import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
plt.style.use("ggplot")
%matplotlib inline
import seaborn as sns

# 加载训练数据：         
wine = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data",header=None)

wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash','Magnesium', 'Total phenols','Flavanoids', 'Nonflavanoid phenols', 
                'Proanthocyanins','Color intensity', 'Hue','OD280/OD315 of diluted wines','Proline']

# 数据查看：
print("Class labels:",np.unique(wine["Class label"]))#有三类葡萄酒
wine.head()

Class labels: [1 2 3]

	Class label	Alcohol	Malic acid	Ash	Alcalinity of ash	Magnesium	Total phenols	Flavanoids	Nonflavanoid phenols	Proanthocyanins	Color intensity	Hue	OD280/OD315 of diluted wines	Proline
0	1	14.23	1.71	2.43	15.6	127	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065
1	1	13.20	1.78	2.14	11.2	100	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050
2	1	13.16	2.36	2.67	18.6	101	2.80	3.24	0.30	2.81	5.68	1.03	3.17	1185
3	1	14.37	1.95	2.50	16.8	113	3.85	3.49	0.24	2.18	7.80	0.86	3.45	1480
4	1	13.24	2.59	2.87	21.0	118	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735

数据预处理

# 数据预处理
# 仅仅考虑2，3类葡萄酒，去除1类
wine = wine[wine['Class label'] != 1]
y = wine['Class label'].values
#仅仅考虑两个特征“Alcohol”和“OD280/OD315 of diluted wines”
X = wine[['Alcohol','OD280/OD315 of diluted wines']].values
# print(X,y)

# 将分类标签变成二进制编码：
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y)

# 按8：2分割训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1,stratify=y)  # stratify参数代表了按照y的类别等比例抽样

使用单一决策树建模

DecisionTreeClassifier——决策树分类器

参数：

criterion：特征选择标准，有“gini”和“entropy”,默认为“gini”
splitter：特征划分标准，有“best”和“random”,"best"适合样本量不大，"random"适合样本量非常大
max_depth：决策树的深度

from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=1)
from sklearn.metrics import accuracy_score
tree = tree.fit(X_train,y_train)
y_train_pred = tree.predict(X_train) # 根据决策树模型用训练集预测
y_test_pred = tree.predict(X_test) # 根据决策树模型用测试集预测
tree_train = accuracy_score(y_train,y_train_pred)
tree_test = accuracy_score(y_test,y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))

Decision tree train/test accuracies 0.916/0.875

实现Adaboost(基分类器为决策树)

参数：

base_estimator:基分类器，默认是DecisionTreeClassifier(max_depth=1)
n_estimators：终止学习时的迭代次数，完全拟合时会提前结束迭代
learning_rate：学习率
algorithm：训练算法{‘SAMME’，‘SAMME.R’}，默认=‘SAMME.R’，两者的区别主要是弱学习器权重的度量，前者是对样本集预测错误的概率进行划分的，后者是对样本集的预测错误的比例，即错分率进行划分的
random_state：随机种子

from sklearn.ensemble import AdaBoostClassifier
ada = AdaBoostClassifier(base_estimator=tree,n_estimators=500,learning_rate=0.1,random_state=1)
ada = ada.fit(X_train,y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train,y_train_pred)
ada_test = accuracy_score(y_test,y_test_pred)
print('Adaboost train/test accuracies %.3f/%.3f' % (ada_train,ada_test))

Adaboost train/test accuracies 1.000/0.917

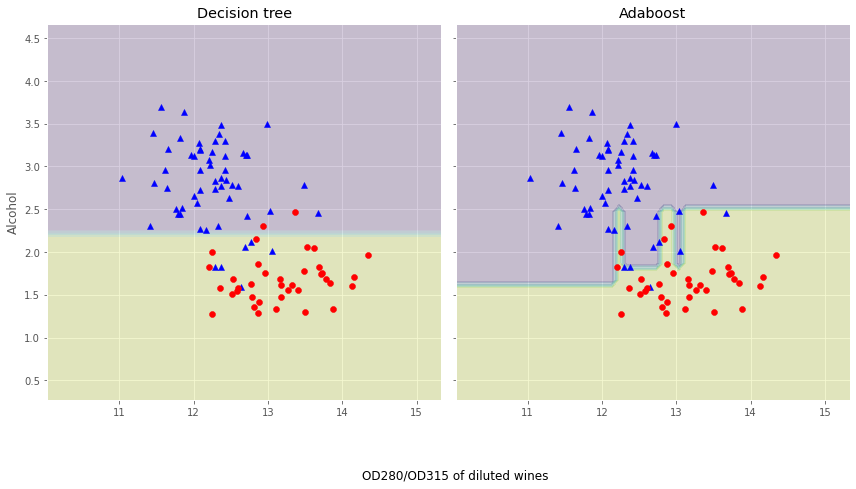
画出单层决策树与Adaboost的决策边界

x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1
print(x_min,x_max,y_min,y_max)
print("----------------")
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))
# print(xx)
print("----------------")
# print(yy)
print("----------------")
print(xx.shape,yy.shape)
print("----------------")
x_train_fake = np.c_[xx.ravel(), yy.ravel()]#这个操作可以把平面上的点都表示出来，继而表示整个平面
# print(x_train_fake)
print("----------------")
# print(x_train_fake.shape)

---------------------------------------------------------------------------

NameError                                 Traceback (most recent call last)

<ipython-input-3-3c4fe75b2756> in <module>
----> 1 x_min = X_train[:, 0].min() - 1
      2 x_max = X_train[:, 0].max() + 1
      3 y_min = X_train[:, 1].min() - 1
      4 y_max = X_train[:, 1].max() + 1
      5 print(x_min,x_max,y_min,y_max)


NameError: name 'X_train' is not defined

# z_fake = tree.predict(x_train_fake)
# z_fake = z_fake.reshape(xx.shape)
# z_fake
# print(X_train.dtype)

# print(y_train)

# print(X_train[y_train==0])

print(X_train[y_train==0,0])# y_train == 0是取的特定的行，0是取的第一列

[12.33 11.56 12.07 11.96 12.16 12.37 12.67 12.37 12.08 12.37 13.03 11.87
 12.08 12.69 11.41 12.08 12.04 12.42 12.21 12.72 12.7  13.49 12.29 12.42
 12.72 12.08 12.08 12.22 12.34 12.6  12.25 12.29 11.79 12.29 12.29 11.03
 12.37 11.65 11.64 11.82 12.   12.   12.52 11.45 11.82 12.99 11.84 12.43
 11.76 13.05 11.46 13.67 12.77 12.64 11.62 12.42 12.47]

f, axarr = plt.subplots(nrows=1, ncols=2,sharex='col',sharey='row',figsize=(12, 6))
for index, clf, title in zip([0, 1],[tree, ada],['Decision tree', 'Adaboost']):
    clf.fit(X_train, y_train)
    # np.c_按行连接矩阵，当传入一维数组时，将一维数组作为列放入到二维数组中，np.r_按列连接矩阵,当传入一维数组时，将两个一维数组连接
    # ravel()实现多维数组扁平化，降为一维数组
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])# 对平面上的所有点都进行预测
    Z = Z.reshape(xx.shape)
    axarr[index].contourf(xx, yy, Z, alpha=0.2)
    axarr[index].scatter(X_train[y_train==0, 0],X_train[y_train==0, 1],c='blue', marker='^')
    axarr[index].scatter(X_train[y_train==1, 0],X_train[y_train==1, 1],c='red', marker='o')
    axarr[index].set_title(title)
axarr[0].set_ylabel('Alcohol', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2,s='OD280/OD315 of diluted wines',ha='center',va='center',fontsize=12,transform=axarr[1].transAxes)
plt.show()

(xx, yy, Z, alpha=0.2)
axarr[index].scatter(X_train[y_train0, 0],X_train[y_train0, 1],c=‘blue’, marker=’^’)
axarr[index].scatter(X_train[y_train1, 0],X_train[y_train1, 1],c=‘red’, marker=‘o’)
axarr[index].set_title(title)
axarr[0].set_ylabel(‘Alcohol’, fontsize=12)
plt.tight_layout()
plt.text(0, -0.2,s=‘OD280/OD315 of diluted wines’,ha=‘center’,va=‘center’,fontsize=12,transform=axarr[1].transAxes)
plt.show()