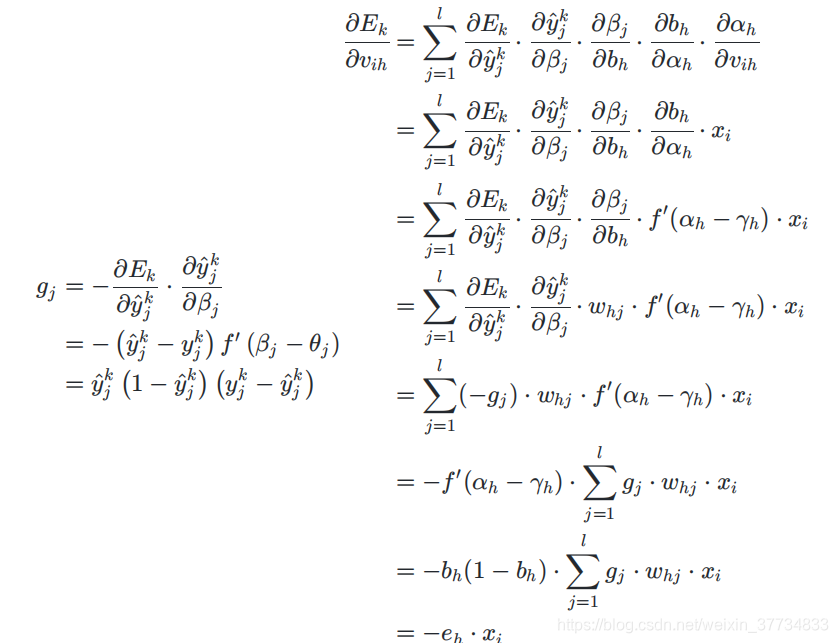5.1 MP神经元
模拟生物神经元,接受n个输入并得到加权和,和自身特有的阈值进行比较(作差),经过激活函数得到输出结果。
单MP神经元:感知机,对数几率回归(逻辑回归)
多MP神经元:神经网络
可以建模成之前我们熟悉的线性模型y=wx+b
激活函数sgn函数(阶跃函数)、sigmoid…
5.2 感知机
5.2.1 数学角度

5.2.2 几何角度
只能解决线性可分的问题
三要素:(模型、策略、算法)
模型:

策略:分错的时候算损失函数

最小化损失函数
将阈值固定为-1,简化模型。
算法:随机梯度下降

由于像感知机这种单个神经元分类能力有限,只能分类线性可分的数据集,对于线性不 可分的数据集则无能为力,但是多个神经元构成的神经网络能够分类线性不可分的数据集(西瓜书上异或问题的那个例子),且有理论证明(通用近似定理):只需一个包含 足够多神经元的隐层,多层前馈网络(最经典的神经网络之一)就能以任意精度逼近任意复杂度的连续函数。因此,神经网络既能做回归,也能做分类,而且不需要复杂的特 征工程。
BUT,理想很丰满,现实很骨感,神经网络存在如下问题待屏幕前的你来解决:
- 面对一个具体场景,神经网络该做多深?多宽?
- 面对一个具体场景,神经网络的结构该如何设计才最合理?
- 对一个具体场景,神经网络的输出结果该如何解释?
5.3 神经网络
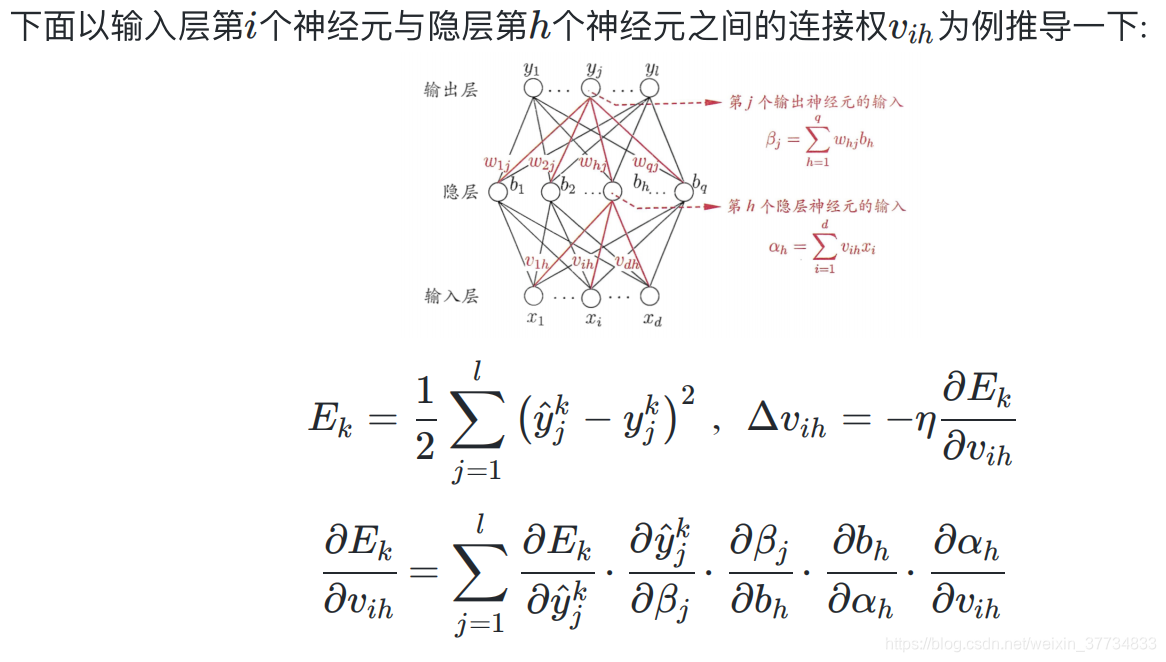
5.3.1 多层前馈神经:全连接
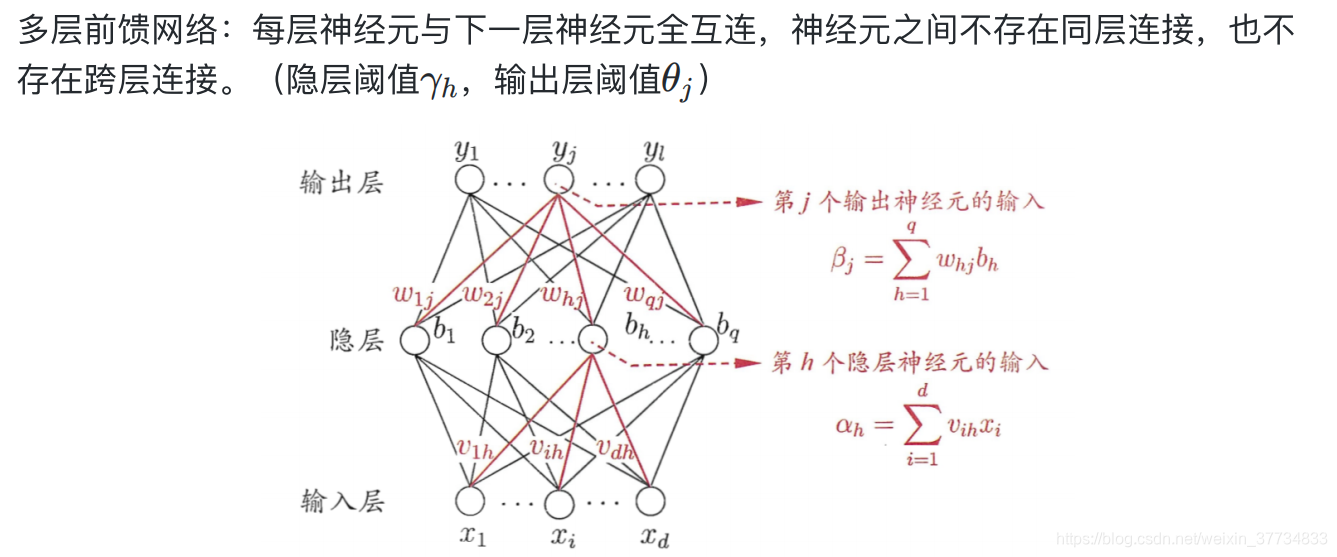
5.3.2 分类、回归

主要限制:数据量、特征(神经网络解放了人力)
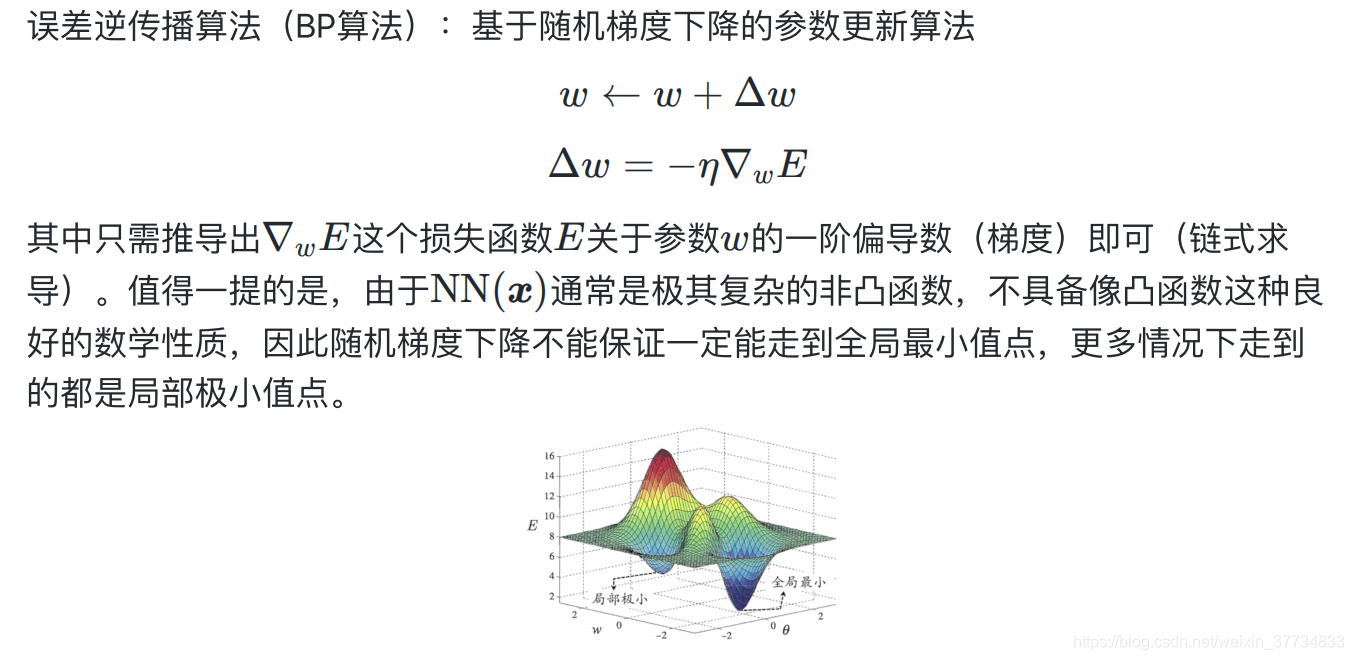
5.3.3 BP反向传播算法