[人工智能]pytorch学习（十四）——权重衰退

1. 如何缓解过拟合？

（1）可以通过收集更多的训练数据来缓解，但是这种方法成本高，而且不受人为控制，短时间内很难取得很高的成效；
（2）也可以通过限制特征的数量来缓解过拟合，但简单地丢弃某些特征会对训练结果产生更多的影响。
（3）假设我们已经拥有了足够多的高质量数据，我们可以用正则化技术来缓解过拟合的影响。

2. 如何衡量模型的复杂度？

记住：模型越复杂，其能拟合的函数也就越复杂，但其也越是容易过拟合；但是模型过于简单，又很容易导致欠拟合，不能够学习到数据的关键特征。

正则化是基于一个基本直觉，即在所有函数$f$中，函数$f=0$（所有输入都得到值$0$）在某种意义上是最简单的，我们可以通过函数与零的距离来衡量函数的复杂度。但是我们应该如何精确地测量一个函数和零之间的距离呢？没有一个正确的答案。事实上，整个数学分支，包括函数分析和巴拿赫空间理论，都在致力于回答这个问题。

一种简单的方法是通过线性函数$f(\mathbf{x})={\mathbf{w}}^{?}\mathbf{x}$中的权重向量的某个范数来度量其复杂性，例如$\Vert \mathbf{w}{\Vert }^2$。要保证权重向量比较小，最常用方法是将其范数作为惩罚项加到最小化损失的问题中。

$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{?}{\mathbf{x}}^{(i)}+b?y^{(i)}\right)}^2.$$

3. 通过限制参数的选择范围来控制模型容量（复杂度）

1. 使用均方范数作为硬性限制
   $$minL(w,b)subjectto||w|{|}^2?\theta$$
   * 通常不限制偏移b（限制与不限制的区别不大）
   * 小$\theta$表示更强的正则项
2. 使用均方范数作为柔性限制
   * 对于每个$\theta$都可以找到$\lambda$使得之前的目标函数等价于下面公式（使用拉格郎日乘子证明）：
   $$minL(w,b)+\frac{\lambda }{2}||w|{|}^2$$
   * 超参数$\lambda$控制了正则项的重要程度
   * $\lambda =0$:无作用
   * $\lambda \to \infty$：$w^{?}\to 0$

4. 正则化如何让权重衰退？

• 计算梯度
  $$\frac{?}{?w}（L（w,b）+\frac{\lambda }{2}{||w||}^2）=\frac{?L(w,b)}{?w}+\lambda w$$

• 时间t更新参数
  $$w_{t+1}=w_t?\eta (\frac{?L(w_t,b)}{?w_t}+\lambda w_t)$$
  $$w_{t+1}=(1?\eta \lambda )w_t?\eta \frac{?L(w_t,b_t)}{?w_t}$$

  • $\eta$为学习率
  • 通常$\eta \lambda <1$，在深度学习中通常称之为权重衰退

可以看出来加上正则项的loss function的梯度只是在$w_t$这里加上了一个$?\eta \lambda$项，通常$?\eta \lambda <1$那么我们得到的梯度更新量就会在梯度更新的方向上回退一些，从而控制了梯度更新的步子。

5. 可视化地看看正则化是如何利用权重衰退来达到缓解过拟合的目的的

权重衰退代码实现(李沐沐神2021动手学深度学习课程中的教学代码)：
训练的公式为：
$$y=0.05+\sum _{i=1}^{d}0.01x_i+?\text{?where?}?～\mathcal{N}(0,0.01^2).$$
我们选择标签是关于输入的线性函数。标签同时被均值为0，标准差为0.01高斯噪声破坏。为了使过拟合的效果更加明显，我们可以将问题的维数增加到$d=200$，并使用一个只包含20个样本的小训练集。

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

# 训练样本20，测试样本100个，输入特征维度200，批次大小5(训练样本太小，很容易过拟合)
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

# 初始化模型参数
def init_params():
    w = torch.normal(0,1,size =(num_inputs,1),requires_grad=True)
    b = torch.zeros(1,requires_grad=True)
    return [w,b]

# 定义L2范数惩罚
def l2_penalty(w):
    return torch.sum(w.pow(2))/2

# 定义训练函数
def train(lambd):
    w,b = init_params()
    net,loss = lambda X:d2l.linreg(X,w,b),d2l.squared_loss
    num_epochs ,lr = 500,0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X,y in train_iter:
            l = loss(net(X),y)+lambd*l2_penalty(w)
            l.sum().backward()
            d2l.sgd([w,b],lr,batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
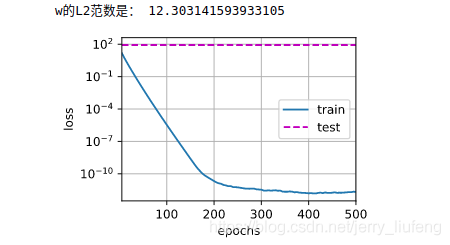
    print('w的L2范数是：', torch.norm(w).item())

# 忽略正则化直接训练
train(lambd=0)

# 使用权重衰减
train(lambd=3)

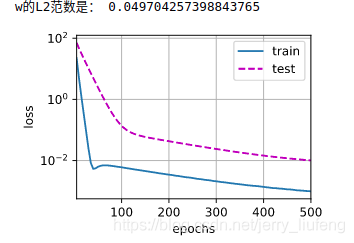
由此可见正则化进行权重衰退的却是缓解了过拟合的问题（未加正则化时，其训练误差和测试误差相差巨大，明显过拟合）。

6. 为什么使用平方范数而非标准范数（欧几里得距离）？

$$L(\mathbf{w},b)+\frac{\lambda }{2}\Vert \mathbf{w}{\Vert }^2,$$

对于$\lambda =0$，我们恢复了原来的损失函数。对于$\lambda >0$，我们限制$\Vert \mathbf{w}\Vert$的大小。公式中除以$2$：当我们取一个二次函数的导数时，$2$和$1/2$会抵消，以确保更新表达式看起来既漂亮又简单。

所以采用平方范数的原始是为了便于计算。通过平方$L_2$范数，我们去掉平方根，留下权重向量每个分量的平方和。这使得惩罚的导数很容易计算：导数的和等于和的导数。

7. L1范数和L2范数在应用中的一些区别

L1范数和L2范数在整个统计学习领域都是有效而受欢迎的正则化方法。

• L1正则化线性回归是统计学习中的基本模型，通常称之为“套索回归”（lasso regression）
  • L1范数施加的惩罚较之L2范数更小，使得模型将其他权重清零，而将权重主要集中在一小部分特征上，也被称之为“特征选择”，在某些情景下这是非常重要和被需要的。
• L2正则化线性模型则构建成了经典的“岭回归”（ridge regression）
  • L2范数对权重向量施加了巨大的惩罚，使得我们的学习算法偏向于在大量特征上均匀分布权重的模型（也就是说使得模型对单个变量中的误差更加鲁棒）