GOAL:?to train a model on a variety of learning tasks, such that it can solve new learning tasks using only a small number of training samples.
引言:从人脸识别说起,若一个公司有50个人,需要做一个人脸识别系统。倘若按照传统的深度学习思想,那应该把识别结果分成51类(50个公司成员+1非公司成员)。那么要训练一个这样的系统,我们的数据集需要这收集这50个公司成员和一些非公司成员的大量、各个角度拍摄的照片对该神经网络进行训练。但是事实显然不是这样的。在做人脸识别的时候往往只需要公司成员提供1-2张照片即可。怎么做到的呢?就是今天的few-shot learning的方法,few-shot learning 的目标在于通过小样本的输入完成分类工作。在few-shot learning的术语中,把公司提供的50个人的数据集叫做Support Set,把51个类别叫做51-way,把公司提供的1-2张照片叫做1-shot或2-shot,把做人脸识别实时采集到的图片数据集叫做?query set?。

(1 shot,6 way Support Set)
常见的网络模型:
- Siamese network (孪生网络,改进版)
? ? ? ? 该网络的工作主要包括以下三个过程:
????????1.预训练:目的在于通过一个庞大的数据集(Train set)进行训练,学习获得一个相似性特征提取的函数(Embedding),该函数将一张图片压缩至一个低维度的向量,并且相同类别或具有相似特征的图片具有相似的向量值。
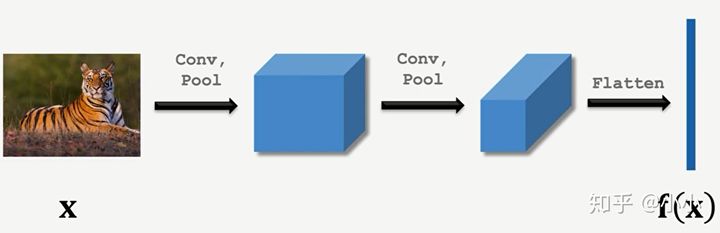
Embedding
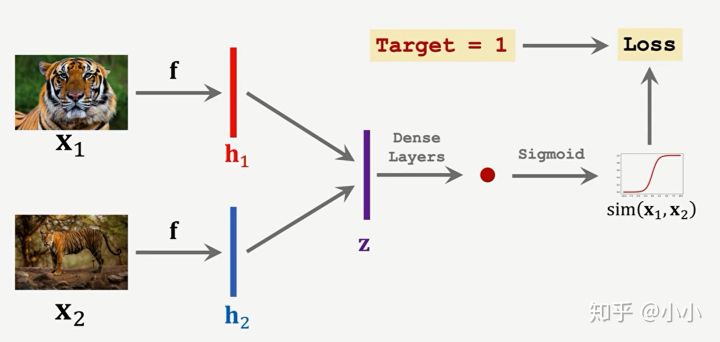
????????????????预训练方法1:learning pair-wise Similarity score,把训练集两两配对,分别经过embadding、FC和Sigmoid后,若为同一类即为1,非同类为0。
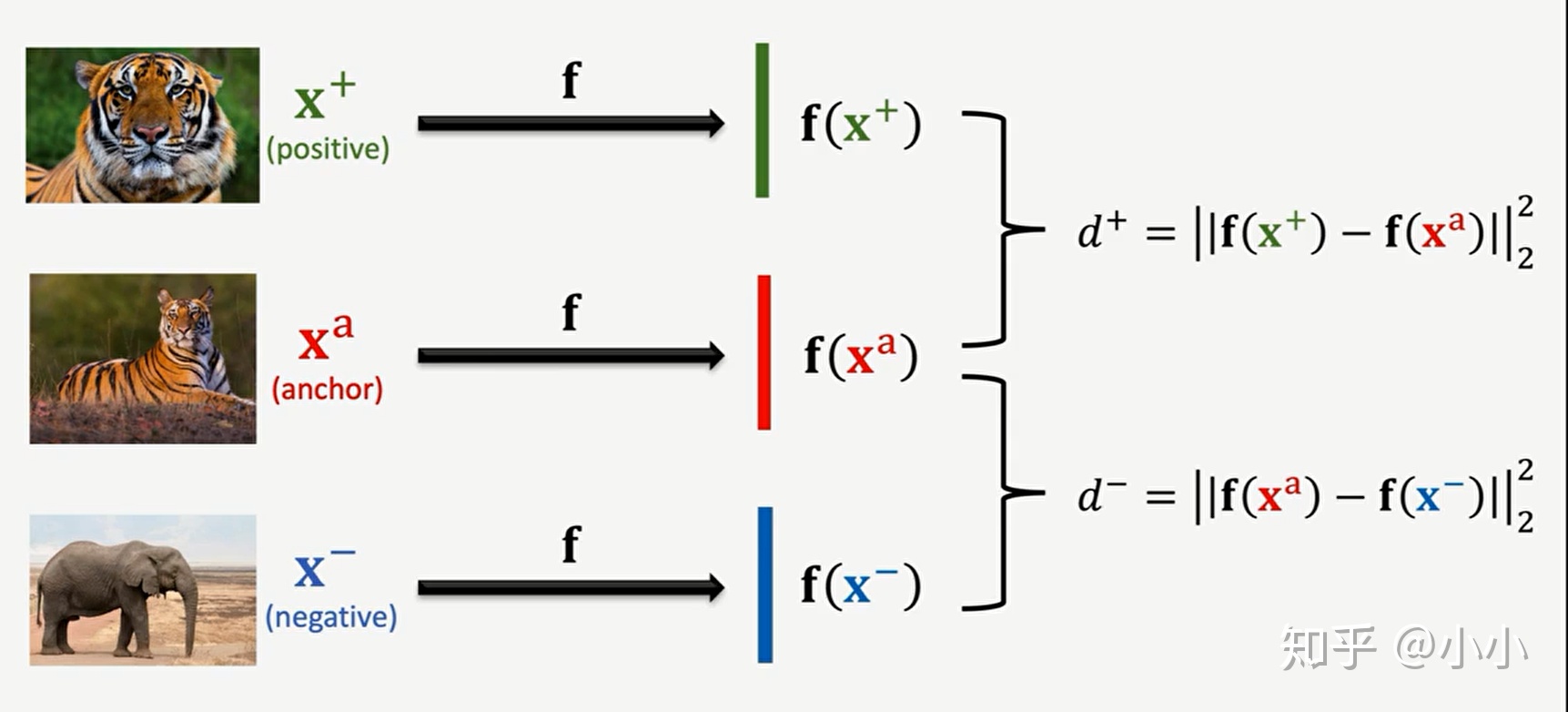
? ? ? ? ????????预训练方法2:Triplet Loss,随机抽出三张图片,一张为主图片(anchor),一张为同类别图像(positive image),另外一种为非同类别图像(negative image),经过embadding后分别计算他们和anchor图像的相似度(distance,以二范数为例)d1和d2,则LOSS=max{0,d1-d2+α },其意义是同类别图像的相似的要大于不同类别的。
????????2.细调(Fine tuning):目的在于根据手上的小数据样本(Support Set),对预训练的模型进行微调,能获得更加良好的效果。
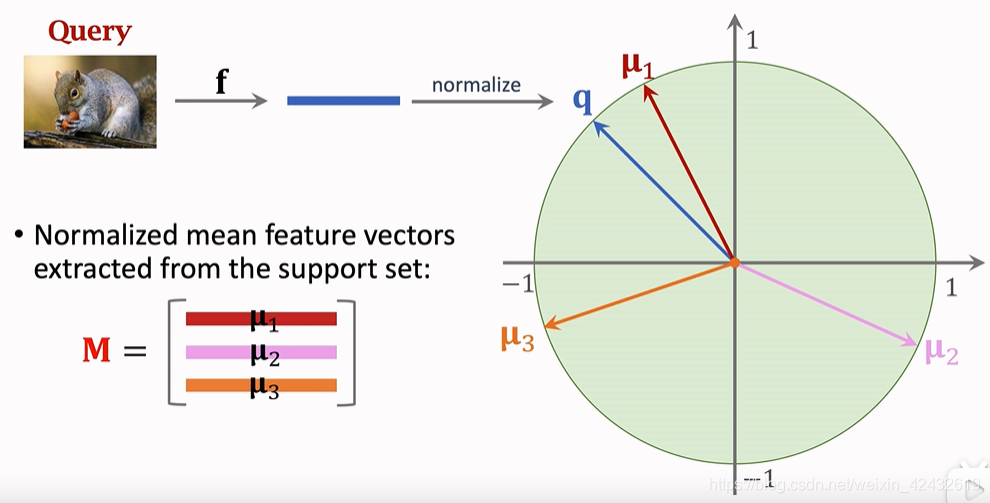
? ? ? ? 首先将Support Set通过预训练的网络进行embadding,获得特征向量后进行归一化得到向量M=[μ1,μ2,μ3]
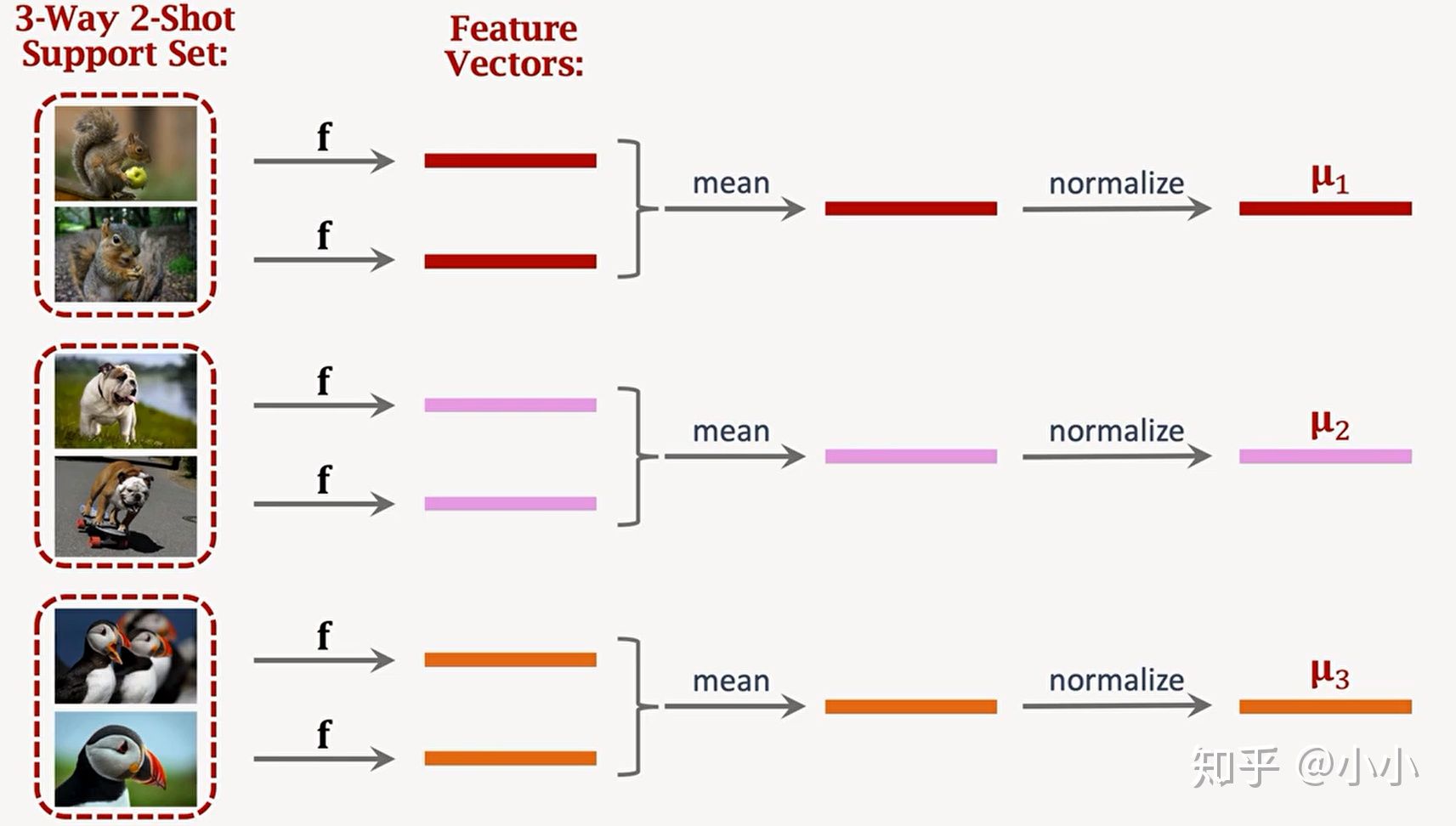
????????得到向量M后,把向量M作为初始化权重,把Support Set中的数据(Xi,Yi)作为输入,计算其余弦距离就能得到分类结果,把分类结果与Yi做对比得到Loss函数,从而对分类器进行微调(Fine tuning),通常Loss函数取交叉熵(CrossEntropy),为了防止过拟合,通常进行正则化,正则化函数采用Entropy Regulation。
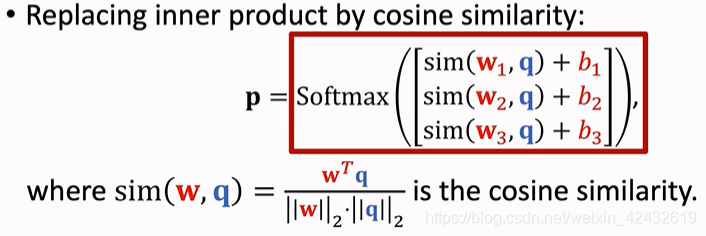
(在fine tuning中图片中的q应该改为Xi)
?
????????3.测试:利用该模型对随机样本(query set)进行测试,观察其分类效果。
?参考内容:https://www.bilibili.com/video/BV1B44y1r75K/?spm_id_from=autoNext
- Matching Network
Paper:Matching Networks for One Shot Learning
? ? ? ? ?在论文中提到,该模型主要有两个创新点:1. 在模型中采用了attention(softmax)和memory(LSTM)来加速学习,2. 对相同的任务的训练和评估(Test and train conditions must match?)的端对端学习(end to end)
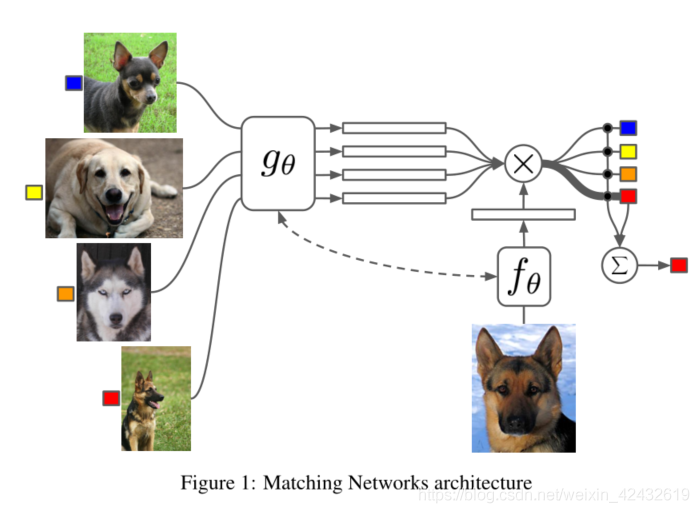
? ? ? ? ?如上图所示,gθ?和fθ?是特征提取函数,把高维度的图像数据压缩成特征向量(Enbadding),通常采用VGG或者Inception?网络(文章后面还使用了LSTM对CNN output进行处理,在文中起名为?fully conditional embeddings,简称FCE),且?gθ?和?fθ 通常取一样的网络,但是论文中提到,取不同的也行。对于所提到的attention机制,主要体现在网络的后半段。
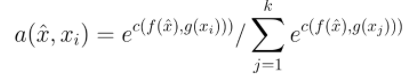
? ? ? ? 上式 a(x,xi) 代表attention,实际是一个softmax函数,c(f(x),g(xi)) 代表余弦相似度函数,x 帽代表query set 的测试输入值,xi代表support set 的样本。该公式的意义在于求得测试样本属于哪一类的概率。
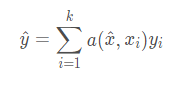
?????????上式 a(x,xi)由上上式子求得,yi为xi对应的类别标签,为one-hot编码,y帽为最终预测值。
? ? ? ? ?对于FCE部分,主要包括两个部分:BidrectionalLSTM 和?AttentionLSTM,前者连接于support set,后者连接于query set,据作者所说这种memory能提高学习效率,其网络结构如下代码所示:
class MatchingNetwork(nn.Module):
def __init__(self, n: int, k: int, q: int, fce: bool, num_input_channels: int,
lstm_layers: int, lstm_input_size: int, unrolling_steps: int, device: torch.device):
"""Creates a Matching Network as described in Vinyals et al.
# Arguments:
n: Number of examples per class in the support set
k: Number of classes in the few shot classification task
q: Number of examples per class in the query set
fce: Whether or not to us fully conditional embeddings
num_input_channels: Number of color channels the model expects input data to contain. Omniglot = 1,
miniImageNet = 3
lstm_layers: Number of LSTM layers in the bidrectional LSTM g that embeds the support set (fce = True)
lstm_input_size: Input size for the bidirectional and Attention LSTM. This is determined by the embedding
dimension of the few shot encoder which is in turn determined by the size of the input data. Hence we
have Omniglot -> 64, miniImageNet -> 1600.
unrolling_steps: Number of unrolling steps to run the Attention LSTM
device: Device on which to run computation
"""
super(MatchingNetwork, self).__init__()
self.n = n
self.k = k
self.q = q
self.fce = fce
self.num_input_channels = num_input_channels
self.encoder = get_few_shot_encoder(self.num_input_channels)
if self.fce:
self.g = BidrectionalLSTM(lstm_input_size, lstm_layers).to(device, dtype=torch.double)
self.f = AttentionLSTM(lstm_input_size, unrolling_steps=unrolling_steps).to(device, dtype=torch.double)
def forward(self, inputs):
pass
class BidrectionalLSTM(nn.Module):
def __init__(self, size: int, layers: int):
"""Bidirectional LSTM used to generate fully conditional embeddings (FCE) of the support set as described
in the Matching Networks paper.
# Arguments
size: Size of input and hidden layers. These are constrained to be the same in order to implement the skip
connection described in Appendix A.2
layers: Number of LSTM layers
"""
super(BidrectionalLSTM, self).__init__()
self.num_layers = layers
self.batch_size = 1
# Force input size and hidden size to be the same in order to implement
# the skip connection as described in Appendix A.1 and A.2 of Matching Networks
self.lstm = nn.LSTM(input_size=size,
num_layers=layers,
hidden_size=size,
bidirectional=True)
def forward(self, inputs):
# Give None as initial state and Pytorch LSTM creates initial hidden states
output, (hn, cn) = self.lstm(inputs, None)
forward_output = output[:, :, :self.lstm.hidden_size]
backward_output = output[:, :, self.lstm.hidden_size:]
# g(x_i, S) = h_forward_i + h_backward_i + g'(x_i) as written in Appendix A.2
# AKA A skip connection between inputs and outputs is used
output = forward_output + backward_output + inputs
return output, hn, cn
class AttentionLSTM(nn.Module):
def __init__(self, size: int, unrolling_steps: int):
"""Attentional LSTM used to generate fully conditional embeddings (FCE) of the query set as described
in the Matching Networks paper.
# Arguments
size: Size of input and hidden layers. These are constrained to be the same in order to implement the skip
connection described in Appendix A.2
unrolling_steps: Number of steps of attention over the support set to compute. Analogous to number of
layers in a regular LSTM
"""
super(AttentionLSTM, self).__init__()
self.unrolling_steps = unrolling_steps
self.lstm_cell = nn.LSTMCell(input_size=size,
hidden_size=size)
def forward(self, support, queries):
# Get embedding dimension, d
if support.shape[-1] != queries.shape[-1]:
raise(ValueError("Support and query set have different embedding dimension!"))
batch_size = queries.shape[0]
embedding_dim = queries.shape[1]
h_hat = torch.zeros_like(queries).cuda().double()
c = torch.zeros(batch_size, embedding_dim).cuda().double()
for k in range(self.unrolling_steps):
# Calculate hidden state cf. equation (4) of appendix A.2
h = h_hat + queries
# Calculate softmax attentions between hidden states and support set embeddings
# cf. equation (6) of appendix A.2
attentions = torch.mm(h, support.t())
attentions = attentions.softmax(dim=1)
# Calculate readouts from support set embeddings cf. equation (5)
readout = torch.mm(attentions, support)
# Run LSTM cell cf. equation (3)
# h_hat, c = self.lstm_cell(queries, (torch.cat([h, readout], dim=1), c))
h_hat, c = self.lstm_cell(queries, (h + readout, c))
h = h_hat + queries
return h
- ?Prototypical Networks(原型网络)
paper:Prototypical Networks for Few-shot Learning
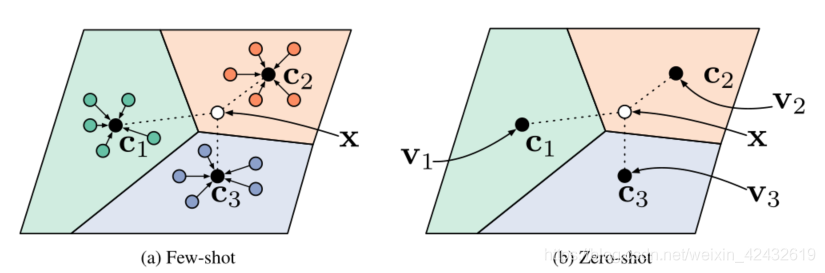
? ? ? ? ?优点在于非常简单,且据文章所述,具有与?Matching Network?相似的精度。其基本思想与kNN(最邻近算法)一致,主要包括以下三个过程:
????????1)embedding,把图像(few-shot,左图)或者描述的元信息(zero-shot,meta-learning,右图)压缩为低维度的特征向量;
 ?
?
def get_few_shot_encoder(num_input_channels=1) -> nn.Module:
"""Creates a few shot encoder as used in Matching and Prototypical Networks
# Arguments:
num_input_channels: Number of color channels the model expects input data to contain. Omniglot = 1,
miniImageNet = 3
"""
return nn.Sequential(
conv_block(num_input_channels, 64),
conv_block(64, 64),
conv_block(64, 64),
conv_block(64, 64),
Flatten(),
)
def conv_block(in_channels: int, out_channels: int) -> nn.Module:
"""Returns a Module that performs 3x3 convolution, ReLu activation, 2x2 max pooling.
# Arguments
in_channels:
out_channels:
"""
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, 3, padding=1),
nn.BatchNorm2d(out_channels),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)????????2)对于Support Set的每一个类别(way/class),计算其特征向量的中心点(class prototype),其实就是一个求解均值的过程:
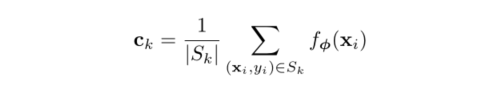
def compute_prototypes(support: torch.Tensor, k: int, n: int) -> torch.Tensor:
"""Compute class prototypes from support samples.
# Arguments
support: torch.Tensor. Tensor of shape (n * k, d) where d is the embedding
dimension.
k: int. "k-way" i.e. number of classes in the classification task
n: int. "n-shot" of the classification task
# Returns
class_prototypes: Prototypes aka mean embeddings for each class
"""
# Reshape so the first dimension indexes by class then take the mean
# along that dimension to generate the "prototypes" for each class
class_prototypes = support.reshape(k, n, -1).mean(dim=1)
return class_prototypes? ? ? ? 3)对于Query Set 的数据X,计算其属于每一类的概率,其实就是一个Softmax的计算,但是值得一提的是,论文中证明(证明过程没看懂)计算相似度时,应该使用布雷格曼散度(?Bregman divergences,也就是欧几里得距离)
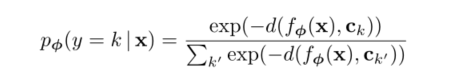
def pairwise_distances(x: torch.Tensor,
y: torch.Tensor,
matching_fn: str) -> torch.Tensor:
"""Efficiently calculate pairwise distances (or other similarity scores) between
two sets of samples.
# Arguments
x: Query samples. A tensor of shape (n_x, d) where d is the embedding dimension
y: Class prototypes. A tensor of shape (n_y, d) where d is the embedding dimension
matching_fn: Distance metric/similarity score to compute between samples
"""
n_x = x.shape[0]
n_y = y.shape[0]
if matching_fn == 'l2':
distances = (
x.unsqueeze(1).expand(n_x, n_y, -1) -
y.unsqueeze(0).expand(n_x, n_y, -1)
).pow(2).sum(dim=2)
return distances
elif matching_fn == 'cosine':
normalised_x = x / (x.pow(2).sum(dim=1, keepdim=True).sqrt() + EPSILON)
normalised_y = y / (y.pow(2).sum(dim=1, keepdim=True).sqrt() + EPSILON)
expanded_x = normalised_x.unsqueeze(1).expand(n_x, n_y, -1)
expanded_y = normalised_y.unsqueeze(0).expand(n_x, n_y, -1)
cosine_similarities = (expanded_x * expanded_y).sum(dim=2)
return 1 - cosine_similarities
elif matching_fn == 'dot':
expanded_x = x.unsqueeze(1).expand(n_x, n_y, -1)
expanded_y = y.unsqueeze(0).expand(n_x, n_y, -1)
return -(expanded_x * expanded_y).sum(dim=2)
else:
raise(ValueError('Unsupported similarity function'))
- ?MAML (Model-Agnostic Meta-Learning,与模型无关的元学习)
paper:Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
? ? ? ? 关于模型无关性(Model-Agnostic),作者如是说:它适用于任何使用梯度下降的模型,包括分类、回归和强化学习。
? ? ? ? 核心思路:训练模型的初始参数,使得这些参数在新任务的小数据中进行一次或多次的梯度更新后就能得到良好的效果。
? ? ? ? 上面两个描述是不是觉得很玄乎但是又有一点点牛皮?都是直译作者原文的,这篇论文前半段疯狂地在用各种表达重复上面这两个观点,卖关子、故弄玄虚。其实描述核心内容就那么一点点。主要包括以下三个步骤:
? ? ? ? 第一,对于一个较大的数据集(任务)?T,将其划分为很多个小数据集(任务)?Ti (meta-batch),并把数据集(任务)?Ti 分割为两个部分,分别为K个样本和N-K个样本;
for meta_batch in x:
# By construction x is a 5D tensor of shape: (meta_batch_size, n*k + q*k, channels, width, height)
# Hence when we iterate over the first dimension we are iterating through the meta batches
x_task_train = meta_batch[:n_shot * k_way]
x_task_val = meta_batch[n_shot * k_way:]? ? ? ? 第二,随机初始化生成一个模型权重参数?θ,对于每一个小数据集(任务)?Ti,抽取数据集内部 K?个样本进行训练并通过梯度下降法更新得到一个与这个小数据集对应的模型新权重参数?θi:
![]()
# Train the model for `inner_train_steps` iterations
for inner_batch in range(inner_train_steps):
# Perform update of model weights
y = create_nshot_task_label(k_way, n_shot).to(device)
logits = model.functional_forward(x_task_train, fast_weights)
loss = loss_fn(logits, y)
gradients = torch.autograd.grad(loss, fast_weights.values(), create_graph=create_graph)
# Update weights manually
fast_weights = OrderedDict(
(name, param - inner_lr * grad)
for ((name, param), grad) in zip(fast_weights.items(), gradients) # zip 打包成元组
)????????第三,训练完每一个的小数据集(任务)?Ti?后都会得到一个模型新权重参数?θi,取该数据集剩下来的?N-K?个数据样本基于该新权重参数?θi,求取每个小数据集对应的?Loss?和?梯度?:
# Do a pass of the model on the validation data from the current task
# 用测试集测试更新后的参数,保存task_predictions 和 task_losses 和 task_gradients
y = create_nshot_task_label(k_way, q_queries).to(device)
logits = model.functional_forward(x_task_val, fast_weights)
loss = loss_fn(logits, y)
loss.backward(retain_graph=True)
# Get post-update accuracies
y_pred = logits.softmax(dim=1)
task_predictions.append(y_pred)
# Accumulate losses and gradients
task_losses.append(loss)
gradients = torch.autograd.grad(loss, fast_weights.values(), create_graph=create_graph)
named_grads = {name: g for ((name, _), g) in zip(fast_weights.items(), gradients)}
task_gradients.append(named_grads)? ? ? ? 然后就是对这些不同小数据?Ti?得到?梯度?进行求和:(这代码看不懂,呜呜呜)
sum_task_gradients = {k: torch.stack([grad[k] for grad in task_gradients]).mean(dim=0)
for k in task_gradients[0].keys()}
hooks = []
for name, param in model.named_parameters():
hooks.append(
param.register_hook(replace_grad(sum_task_gradients, name))
)
? ? ? ? 最后是基于求和的梯度参数进行权重更新 (model()函数里面的参数是什么鬼,定义是:
def __init__(self, num_input_channels: int, k_way: int, final_layer_size: int = 64)
? ? ? ? 还有是什么时候把之前求和的梯度参数传进去的???)
model.train()
optimiser.zero_grad()
# Dummy pass in order to create `loss` variable
# Replace dummy gradients with mean task gradients using hooks
logits = model(torch.zeros((k_way, ) + data_shape).to(device, dtype=torch.double))
loss = loss_fn(logits, create_nshot_task_label(k_way, 1).to(device))
loss.backward()
optimiser.step()
for h in hooks:
h.remove()代码来源:https://github.com/oscarknagg/few-shot
---------------------------
---------------------------
---------头秃.jpg--------
----------------------------
----------------------------
- 我的理解:
- 为什么MAML适用于小数据?因为倘若直接训练,数据集很小,一小会功夫就训练完了,得到的模型也不太好,因此作者采用了一个对类别随机组合抽样的机制,对数据进行多次利用;
- 为什么meta-update要对Loss函数先进行基于Task batch的求和后求导呢,而不是直接的梯度下降呢?因为直接使用梯度下降的最理想结果是使得求解收敛于局部的最优解,但是MAML并不希望这样,它希望的是更好的适应性,也就是说在新的任务进来时,通过尽可能的迭代就收敛到新的任务的最优解里面,因此训练时应该到达一个“中间位置“,因此采用求和求导(求导和求和的运算是可以交换的)。
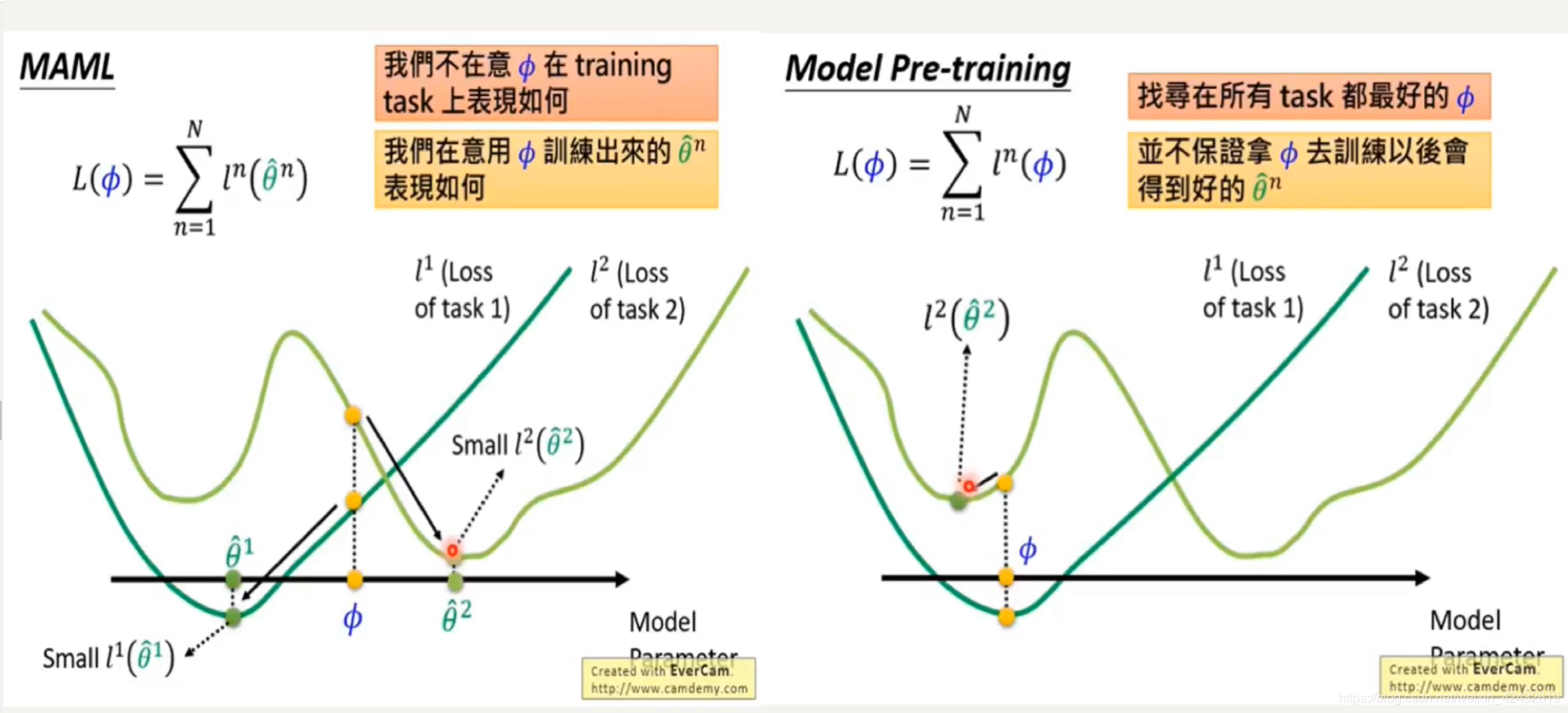
- ?论文中所说的一阶、二阶是什么意思?为什么meta-update采用的是对原始参数θ而不是优化后的参数θi求导?
推导过程来源于:https://www.bilibili.com/video/BV11E411G7V9
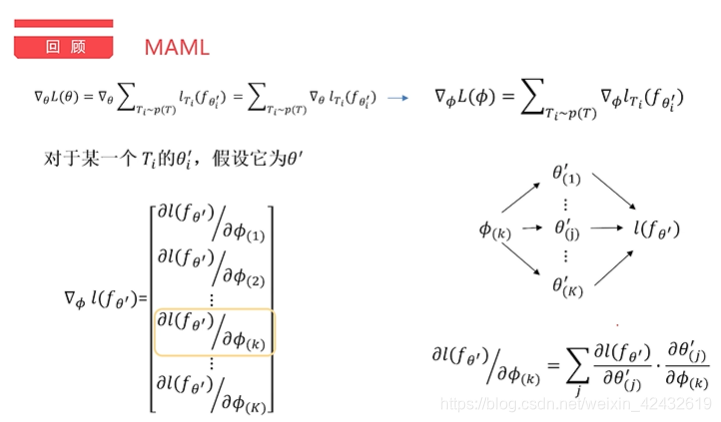
?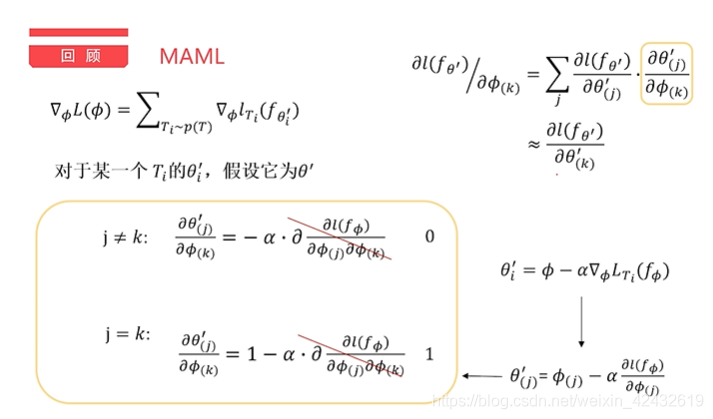
?推导的结果显示:如果忽略二阶的影响,其实最后的结果等效于Loss函数对优化过的θi进行求导,那么二阶有什么影响或者优势吗?其实我也不知道。
?
?
?