第二章 数字图像基础
2.1视觉感知要素
? ? ?这一节主要以讨论人眼中形成图像最基本的机理与参数,将通过数字图像处理的一些因素去了解人类视觉的物理限制。
2.1.1人眼的构造与传感器
? ? 人眼具体的构造不在此处说明。眼睛的内部具有视网膜,而视网膜表面分布着有光分离接收器。光分离接收器提供了图案视觉。光接收器分为两类:一类是锥状体,一类是杆状体。锥状体主要分布在中央凹,对颜色的灵敏度非常高。肌肉控制眼球转动,直到物体成像落在中央凹上。锥状视觉被称为白昼视觉或者亮光视觉。;杆状体主要分布与视网膜的表面,杆状体可以给出视野内一般的总体图像。它们没有彩色感觉,而在低照明度下对图像较为敏感。因此杆状体视觉也被称为夜视觉或者暗视觉。
? ? 基于以上的大致成像原理,我们可以将一个大小为1.5mm*1.5mm的传感器比做成中央凹,分辨率近似。
2.1.2人眼成像机理
? ? 人眼成像类似于小孔成像,由晶状体作为中间的光心,将外界的物体成像于视网膜上,由于光接收器的存在而产生感觉。感觉将辐射能转变成电脉冲,最后由大脑解码。
2.1.3亮度适应和鉴别
? ? 数字图像作为离散的亮点集,因此,由于眼睛对于不同亮度之间的鉴别能力在图像处理结果中是要考虑的重要方面。
? ? 概括来说,人眼具有夜视和昼视,昼视对于光亮度的适应范围要远大于夜视。但是由于人眼具有动态可调节能力,即即便是夜视,眼睛适应某一亮度级时,会延伸一些适应范围。一个描述亮度辨别特性的基本实验表明,(1)低照明级别时刻,视觉由杆状体执行,没有较好的辨别能力;高照明级别时刻,视觉由锥状体执行,有较好的辨别能力;(2)若背景照明保持恒定,人眼可以观察到12到24级不同强度的变化。(事实上,在同一副图像上,由于人眼的适应度,眼睛可以检测到不足24级的全部强度范围。)
? ? 感觉亮度不是简单地强度函数。人眼也具有一定的视觉错觉。
2.2光和电磁波谱
? ? 电磁波谱是条状波谱,描述了不同波长下的波段。电磁波谱了用波长、频率和能量来进行描述,波长和频率可以表示为landa=c/v,c表示光速2.998*10^8,v是频率;能量E=hv,h表示普朗克常量。电磁波可以看成是以波长为landa传播的正弦波,该波以波那样的光速传播,每个粒子包含一定能量,每束能量称为光子。可见伽马射线的能量很大,即伽马射线对活体组织危害很大。
? ? 光是一种特殊的电磁辐射,人眼可以看见和察觉到它。人眼能察觉到的彩色波段范围为0.43um(紫色)—0.79um(红色)的范围,每个颜色波段之间都是颜色平滑过去的。
? ? 人从一个物体感受的颜色由物体反射光的性质所决定。一个物体若反射的可见光波长相对平衡,则对于观察者来说就是白色的,若反射波在一个波长范围内,则会反射某一颜色。
? ? 单色光没有颜色,只有强度或大小。灰度级用来描述单色光强度,范围从黑到灰,到白;彩色光有三个描述基本量,发光强度、光通量和亮度。发光强度指的是从光源流出能量的总量,光通量指的是观察者从光源感受到的能量,如对于观测者,感受不到红外光的能量,则称红外光的光通量几乎为0,最后是强度。
? ?电磁波谱从左端开始分析其实际应用:①伽马射线,伽马辐射对于医学和天文学图像很重要,②硬X射线,主要用于工业,③软X射线,主要应用如胸透X射线,牙科X射线在该短波段的低能段④远红外波段,依靠“热特性”可以用于热成像⑤微波段,微波炉⑥无线电波,应用于AM,FM等收音机。
? ?在原理上,如果一种传感器可以检测一种电磁波谱发射的能量,那么就可以在一波段上对感兴趣的事件成像。
2.3图像感知和获取
? ?“照射”源和形成图像的“场景”元对光能的反射和吸收相互结合产生各类图像。“照射”和“场景”可以是许多不同的元素,如照射可以是电磁能引起,雷达,红外线,x光线等,场景也可以是多种多样,可以是分子,岩石,人体等等。根据光源的性质,可以进行折射和透射两种照射方式,第一种类型有平面成像,第二种类型可以是x光透射成像。
? ?照射量变为数字图像主要有三种传感器装置,(a)单个成像传感器,(b)线性传感器,(c)传感器阵列。
? ?这里不对2.3.1(1)(2)(3)进行详细阐述。单个传感器获取图像的例子有微观光密度计,带状传感器获取图像的例子有CAT,MRI等,传感器阵列获取图像的例子有数码摄像机等。
2.3.4图像形成模型
? ?若用f(x,y)二维函数表示图像,在特定的坐标(x,y)下,f的值或者幅度值都是一个正的标量,其物理意义由图像源来决定。本书多数图像均是单色图,可以用灰度级来进行描述。
? ?f(x,y)一定是非零和有限的,即:0<f(x,y)<∞
? ?f(x,y)可以由两个分量来进行数学表征:(1)入射到观察场景的光源量总和(2)场景中物体反射光的总和。我们相应的将其描述为入射分量和反射分量,分别表示为i(x,y)和r(x,y)。表征方式为:
? ?f(x,y)=i(x,y)r(x,y)
? 这里0<i(x,y)<∞,0<r(x,y)<1。显然r(x,y)所表示的反射分量限制于0(全吸收)和1(全反射)之间,0的时候f(x,y)=0即表示所捕获到的图像信息为0,反射光线全部被吸收;1的时候f(x,y)=i(x,y)此时照射光线全部被反射回来。当然r(x,y)不仅可以表示反射函数,也可以表示透射函数。
? 我们称单色图像在任何坐标(x0,y0)处的强度为图像在那一点的灰度级(l),即
? l=f(x0,y0)
? 显然l存在于一个区间内,区间为[L(min),L(max)]。我们要求L(min)是一个正值,L(max)是一个有限制即可。实际上,L(min)=i(min)r(min),L(max)=i(max)r(max)。
? 区间[L(min),L(max)]称为灰度级。实际上我们常常取灰度级为[0,L-1]。0表示黑色,L-1表示白色,而所有的中间值都是黑色到白色的灰色调。
2.4图像的取样和量化
2.4.1取样和量化的基本概念
? ?基于大多数传感器输出都是连续电压波形,这些波形的幅度和空间特性都与感知的物理现象有关。为了产生数字图像,则我们必须把连续的感知数据转换成为数字形式。其中包含两种处理:取样和量化。

取样和量化基本如图所示,对AB线段展开,得到横坐标与灰度级的关系图,随后对横坐标进行取样,对灰度级进行量化。?
2.4.2数字图像表示
? ? 取样和量化的结果实际上是一个矩阵。假如一幅图像f(x,y)被取样,则产生的数字图像有M行和N列。我们约定矩阵形式如下:
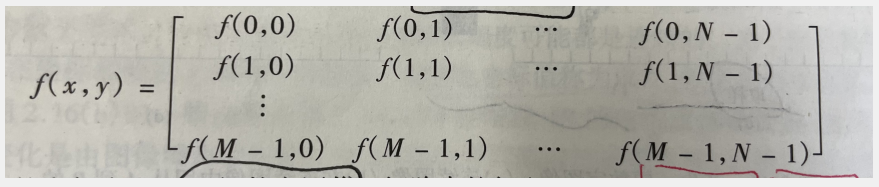
注意坐标(0,1)所表示的含义实际上为沿第一行的第二个取样。
该约定矩阵定义了一幅数字图像,矩阵中的每一个元素都被称为图像单元、图像元素或像素。
当然也可以使用传统矩阵来表示数字图像和像素,这里忽略。
我们对于M,N值的要求是M和N必须取正整数,但是出于硬件要求,灰度级典型的取值是2的整数次幂:L=2^k
灰度级的取值范围我们称为图像的动态范围。我们把占用灰度级全部有效段的图像称为高动态范围图像,此时图像具有较高的对比度。低动态范围的图像看上去冲淡了灰暗格调。
那我们该如何计算数字图像的存储大小(比特数):b=M*N*k
当一幅图像具有2^k灰度级时,我们称该图像是k比特图像。?
2.4.3空间和灰度级分辨率
? ? 一幅图像空间分辨率的主要参数:取样值。空间分辨率是图像中可辨别的最小细节。通俗来讲,取样值越多分辨率越清晰;灰度级分辨率是指灰度级别中可以分辨的最小变化。
? ?通常的,我们把大小为M*N,灰度为L级的数字图像称为空间分辨率M*N,灰度级分辨率为L级的数字图像。
{例1}

该例子可以简要说明取样对空间分辨率的影响。
?{例2}

?
若保持空间分辨率稳定,逐渐减小k值就会得到从(a)-(h)的图像变化?
该例子说面逐渐减小灰度级分辨率对图像的影响
{例3}
我们已经对单幅图像的K值,N值影响图像有所了解,那么K和N之间是否有其他的关系?
现在有三幅图像,(a),(b),(c),它们所包含的细节数量各不相同,逐渐递增

现在将不同K,N值所对应的图像给实验观察者看,让观察者判断图像的质量
我们得到等偏爱曲线
 ?
?
我们发现,(1)当细节越多,灰度级分辨率的影响会逐渐变低,(2)细节多的图像,灰度级在某一范围减小的时候,影响也不大。这可能是由于灰度级分辨率的减少,导致图像对比度增加,产生图像质量改进的视觉效果,(3)空间分辨率对人对图像分辨的影响总是较大。
2.4.4混淆的水纹图样?
2.4.5放大和收缩数字图像
前述我们讨论了抽样和量化的基本知识,我们在一个例题可以了解到如果抽样点少,如32*32,若将其恢复到1024*1024,必有大的失真现象。那么现在就粗略的讨论如何实现,32*32到1024*1024的放大过程。
【放大】
(1)最近邻法,主要有两个步骤:①创立新的像素点位置,②对新的像素点位置进行赋值。如一幅500*500的图像,我们如何放大至750*750?我们可以模拟在原图像中放置虚拟栅格750*750,显然虚拟栅格的间距要比原图像像素点间距要小,为了进行灰度赋值,我们在原图像上寻找最靠近的像素点,并将其灰度值赋予给新的栅格点。
? ? ?最近邻法也有特殊的情况,如果我们的放大倍数是整数倍的,那么我们直接赋值行列的像素点,每隔响应的行数列数进行重复,即可以实现整数倍放大。
(2)双线性插值,由于最近邻法会出现棋盘格效应,则有改进的灰度赋值方法,即双线性插值法。采用四个最邻近的点来对新的像素点赋值。
【收缩】
(1)最近邻法,和放大相反的操作,可以先放置小号的虚拟栅格,然后赋灰度值;或者是整数倍收缩,隔某几行就删除行或列的手段。
(2)双线性插值
基于以上所讲述的两种方法,实际上还有更多邻点的内插方式。更多邻点意味着更复杂表面对点赋灰度值,该种方法常常会产生一些平滑的效果。在三维和医学图像中使用较多。
2.5像素间的一些基本关系
? ? 一幅图像已知用f(x,y)进行表示,当我们指特殊像素时用小写字母(如p和q等)来表示。
2.5.1相邻像素
:表示的是坐标(x,y)的一个像素p的4邻域。即像素p有四个水平和垂直的相邻像素,即(x+1,y)等,每一个像素距(x,y)一个单位距离,如果(x,y)位于图像的边界,则p的某一邻像素位于外部。
:表示的是像素P的4个对角邻像素,即(x+1,y+1)等
:表示的是4个邻域点加4个对角邻像素点,与前边类似,如果p点在边界,则有一些邻域点会消失。

?
2.5.2邻接性、连通性、区域和边界
连通性:讨论p,q两个像素点的连通性,满足两个条件,①两个像素是相邻的,②灰度值是否满足相似性准则(或者说两个像素的灰度值是否相等)。例如,二值图像,两个像素可能是4邻接的,但是仅仅在两像素为同一灰度值时才能说是相通的。
邻接性:首先我们定义一个灰度值集合V。例如在二值图像当中V={1};在灰度图像当中,集合V一般会包含更多的元素,可能是0-255。我们考虑三种类型的邻接性:
(a)4邻接:如果一个像素点q在集合之中,p,q两个像素点的灰度值均在V之中,则称p,q两个像素点是4邻接的。

注:红色箭头所指的两个像素点就是4邻接?
(b)8邻接:如果一个像素点q在集合之中,p,q两个像素点的灰度值均在V之中,则称p,q两个像素点是8邻接的。

?
(c)m邻接(混合邻接):
对于V 假设要p,q两点是m邻接的 则要满足下面两个条件之一即可 ? ? ?
1、q在p的4邻域中, ? ? ?
2、q在p的对角邻域中,并且q的4邻域与p的4领域相交为空集(交集无点属于V)

注:最右侧的图是一个m邻接,中间的图是一个8邻接。
讨论:我们之所以有m邻接的原因是,8邻接常常会发生二义性。那么什么被称之为二义性??在这个图中,8邻域中的中间的那个1可以有两条路到达右上角的那个1,这就是所说的二义性,这个情况在边缘检测里面是很不希望的。
? ? ? ? ? ?而改成m邻域以后,中间的1像素和右上角的像素是8连通的却不是m连通的,这可以从m连通的定义得到,因此,如果用M连通从中间的1到右上角的1就只有一条路。
通俗来讲:当像素间同时存在4邻接和8邻接时,优先采用4邻接,屏蔽和一个像素同时存在4邻接的两个像素之间的8邻接。
关于通路的说明:从一个像素点(x_0 ,y_0)p走到坐标为(s,t)的像素q的通路是特定像素序列,坐标为(x_0,y_0)(x_1,y_1)...(s,t),其中的坐标(x_i,y_i)和(x_i-1,y_i-1)是邻接的。n表示通路长度。若通路回到原点,则称该通路为闭合通路。
通路有4-通路,8-通路,m-通路。这边不再赘述。
区域和边界:首先叙述概念连通集,现在假设S是图像中的一个像素子集合。如果S中全部像素之间存在通路,则可以说存在两个像素点p,q,他们两是在S中连通的。对于S中的任意像素N来说,如果S中有连通到该像素的像素集都被称为连通分量。如果仅有一个连通分量,则被称为连通集。
? ? ? ?如果R现在是一个像素子集,且R是一个连通集,则称R是一个区域。区域的边界(同边缘或轮廓)是区域中像素的集合。
? ? ?边缘和边界有什么区别:边界有“整体”的概念,一个有限区域的边界形成一条闭合通路。边界是由具有某些个导数点所组成的像素集合。简单地说,边界就是区域中像素的集合,边缘是灰度值发生突变的像素点。
2.5.3距离度量
现在定义两个像素点p(x,y),q(s,t),假如这两个点位于一个平面内:
存在好几种距离度量方式:
(1)p,q欧式距离度量方式:
?^(0.5) ,这个方程实际上就是数学上的两点距离,对于该种距离度量,距点(x,y)的距离小于或等于某一值r的像素是,中心在(x,y)半径为r的圆平面。
(2)距离(城市街区距离):
,该距离表示下,距离小于或等于某一值r的像素形成一个中心在(x,y)的菱形。如:

=1的像素是(x,y)的四邻域。
(3)距离(棋盘距离):
,该距离表示下,距离小于或等于某一值r的像素形成中心在(x,y)的方形。如:

?的像素是关于(x,y)的8邻域。
注意,以上所表示的距离关系和通路不存在任何的关系。但是,如果考虑m邻接,则两点间的距离是和通路直接相关的。
例如,
?
?2.5.4基于像素的图像处理
后续的章节进行详细的论述
2.6线性和非线性操作
线性操作对于图像处理来说较为重要,比如,我们假定一个算子H,输入输出均是图像,现在有两副图像f和g,如果有
则称该算子为线性算子。
?
?
