Stacking被称为“懒人算法”,因为它不需要花费过多时间的调参就可以得到一个效果不错的算法,也比bagging和boosting算法容易理解的多。
Stacking严格来说并不是一种算法,而是对模型集成的一种策略。Stacking集成算法可以理解为一个两层的集成,第一层含有多个基础分类器,把预测的结果(元特征)提供给第二层, 而第二层的分类器通常是逻辑回归,他把一层分类器的结果当做特征做拟合输出预测结果。
1.Blending集成学习算法
Blending:简化版的Stacking
Blending集成学习步骤如下:
(1) 将数据划分为训练集和测试集(test_set),其中训练集需要再次划分为训练集(train_set)和验证集(val_set);
(2) 创建第一层的多个模型,这些模型可以是同质的也可以是异质的;
(3) 使用train_set训练步骤2中的多个模型,然后用训练好的模型预测val_set和test_set得到val_predict, test_predict1;
(4) 创建第二层的模型,使用val_predict作为训练集训练第二层的模型;
(5) 使用第二层训练好的模型对第二层测试集test_predict1进行预测,该结果为整个测试集的结果。
优点:实现简单粗暴,没有太多的理论的分析
缺点:Blending只使用了一部分数据集作为留出集进行验证,也就是只能用上数据中的一部分,实际上这对数据来说是很奢侈浪费的
2.Stacking集成学习算法
Blending产生验证集的方式是直接分割,产生一组训练集和验证集;而Stacking采用交叉验证的方式。
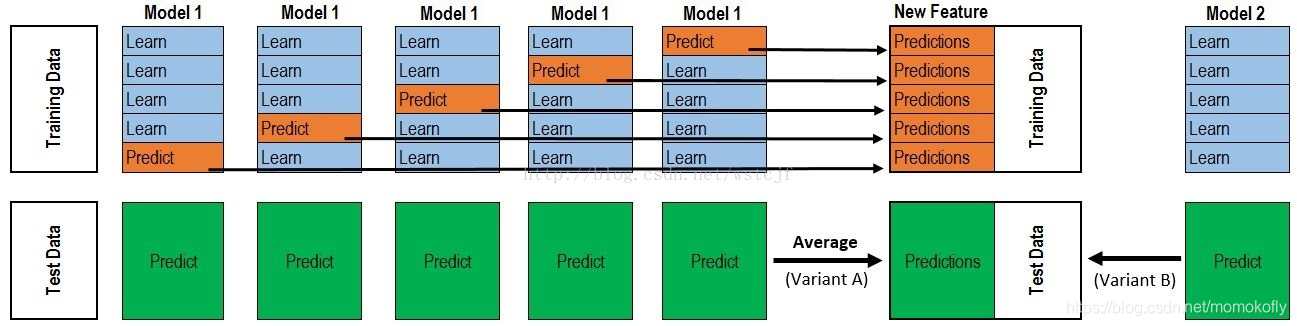
Stacking的完整步骤:
上半部分是用一个基础模型进行5折交叉验证,如:用XGBoost作为基础模型Model1,5折交叉验证就是先拿出四折作为training data,另外一折作为testing data。注意:在stacking中此部分数据会用到整个traing set。如:假设我们整个training set包含10000行数据,testing set包含2500行数据,那么每一次交叉验证其实就是对training set进行划分,在每一次的交叉验证中training data将会是8000行,testing data是2000行。
每一次的交叉验证包含两个过程,1. 基于training data训练模型;2. 基于training data训练生成的模型对testing data进行预测。在整个第一次的交叉验证完成之后我们将会得到关于当前testing data的预测值,这将会是一个一维2000行的数据,记为a1。注意!在这部分操作完成后,我们还要对数据集原来的整个testing set进行预测,这个过程会生成2500个预测值,这部分预测值将会作为下一层模型testing data的一部分,记为b1。因为我们进行的是5折交叉验证,所以以上提及的过程将会进行五次,最终会生成针对testing set数据预测的5列2000行的数据a1,a2,a3,a4,a5,对testing set的预测会是5列2500行数据b1,b2,b3,b4,b5。
在完成对Model1的整个步骤之后,我们可以发现a1,a2,a3,a4,a5其实就是对原来整个training set的预测值,将他们拼凑起来,会形成一个10000行一列的矩阵,记为A1。而对于b1,b2,b3,b4,b5这部分数据,我们将各部分相加取平均值,得到一个2500行一列的矩阵,记为B1。
以上就是stacking中一个模型的完整流程,stacking中同一层通常包含多个模型,假设还有Model2: LR,Model3:RF,Model4: GBDT,Model5:SVM,对于这四个模型,我们可以重复以上的步骤,在整个流程结束之后,我们可以得到新的A2,A3,A4,A5,B2,B3,B4,B5矩阵。
在此之后,我们把A1,A2,A3,A4,A5并列合并得到一个10000行五列的矩阵作为training data,B1,B2,B3,B4,B5并列合并得到一个2500行五列的矩阵作为testing data。让下一层的模型,基于他们进一步训练。
Blending与Stacking对比,Blending的优点和缺点分别为:
优点:比stacking简单(因为不用进行k次的交叉验证来获得stacker feature)
缺点:使用了很少的数据(是划分hold-out作为测试集,并非cv)
blender可能会过拟合(其实大概率是第一点导致的)
stacking使用多次的CV会比较稳健
3.案例分析一:幸福感预测
一个数据挖掘类型的比赛——幸福感预测的baseline。比赛的数据使用的是官方的《中国综合社会调查(CGSS)》文件中的调查结果中的数据,其共包含有139个维度的特征,包括个体变量(性别、年龄、地域、职业、健康、婚姻与政治面貌等等)、家庭变量(父母、配偶、子女、家庭资本等等)、社会态度(公平、信用、公共服务)等特征。
赛题要求使用以上 139 维的特征,使用 8000 余组数据进行对于个人幸福感的预测(预测值为1,2,3,4,5,其中1代表幸福感最低,5代表幸福感最高)。 最终的评价指标为均方误差MSE。
导入package
import os
import time
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from datetime import datetime
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score, roc_curve, mean_squared_error,mean_absolute_error, f1_score
import lightgbm as lgb
import xgboost as xgb
from sklearn.ensemble import RandomForestRegressor as rfr
from sklearn.ensemble import ExtraTreesRegressor as etr
from sklearn.linear_model import BayesianRidge as br
from sklearn.ensemble import GradientBoostingRegressor as gbr
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import LinearRegression as lr
from sklearn.linear_model import ElasticNet as en
from sklearn.kernel_ridge import KernelRidge as kr
from sklearn.model_selection import KFold, StratifiedKFold,GroupKFold, RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn import preprocessing
import logging
import warnings
warnings.filterwarnings('ignore') #消除warning
导入数据集
train = pd.read_csv("train.csv", parse_dates=['survey_time'],encoding='latin-1')
test = pd.read_csv("test.csv", parse_dates=['survey_time'],encoding='latin-1') #latin-1向下兼容ASCII
train = train[train["happiness"]!=-8].reset_index(drop=True)
train_data_copy = train.copy() #删去"happiness" 为-8的行
target_col = "happiness" #目标列
target = train_data_copy[target_col]
del train_data_copy[target_col] #去除目标列
data = pd.concat([train_data_copy,test],axis=0,ignore_index=True)
查看数据的基本信息
train.happiness.describe() #数据的基本信息
数据预处理
首先需要对于数据中的连续出现的负数值进行处理。由于数据中的负数值只有-1,-2,-3,-8这几种数值,所以它们进行分别的操作。
#make feature +5
#csv中有复数值:-1、-2、-3、-8,将他们视为有问题的特征,但是不删去
def getres1(row):
return len([x for x in row.values if type(x)==int and x<0])
def getres2(row):
return len([x for x in row.values if type(x)==int and x==-8])
def getres3(row):
return len([x for x in row.values if type(x)==int and x==-1])
def getres4(row):
return len([x for x in row.values if type(x)==int and x==-2])
def getres5(row):
return len([x for x in row.values if type(x)==int and x==-3])
#检查数据
data['neg1'] = data[data.columns].apply(lambda row:getres1(row),axis=1)
data.loc[data['neg1']>20,'neg1'] = 20 #平滑处理
data['neg2'] = data[data.columns].apply(lambda row:getres2(row),axis=1)
data['neg3'] = data[data.columns].apply(lambda row:getres3(row),axis=1)
data['neg4'] = data[data.columns].apply(lambda row:getres4(row),axis=1)
data['neg5'] = data[data.columns].apply(lambda row:getres5(row),axis=1)
填充缺失值,在这里我采取的方式是将缺失值补全,使用fillna(value),其中value的数值根据具体的情况来确定。例如将大部分缺失信息认为是零,将家庭成员数认为是1,将家庭收入这个特征认为是66365,即所有家庭的收入平均值。
#填充缺失值 共25列 去掉4列 填充21列
#以下的列都是缺省的,视情况填补
data['work_status'] = data['work_status'].fillna(0)
data['work_yr'] = data['work_yr'].fillna(0)
data['work_manage'] = data['work_manage'].fillna(0)
data['work_type'] = data['work_type'].fillna(0)
data['edu_yr'] = data['edu_yr'].fillna(0)
data['edu_status'] = data['edu_status'].fillna(0)
data['s_work_type'] = data['s_work_type'].fillna(0)
data['s_work_status'] = data['s_work_status'].fillna(0)
data['s_political'] = data['s_political'].fillna(0)
data['s_hukou'] = data['s_hukou'].fillna(0)
data['s_income'] = data['s_income'].fillna(0)
data['s_birth'] = data['s_birth'].fillna(0)
data['s_edu'] = data['s_edu'].fillna(0)
data['s_work_exper'] = data['s_work_exper'].fillna(0)
data['minor_child'] = data['minor_child'].fillna(0)
data['marital_now'] = data['marital_now'].fillna(0)
data['marital_1st'] = data['marital_1st'].fillna(0)
data['social_neighbor']=data['social_neighbor'].fillna(0)
data['social_friend']=data['social_friend'].fillna(0)
data['hukou_loc']=data['hukou_loc'].fillna(1) #最少为1,表示户口
data['family_income']=data['family_income'].fillna(66365) #删除问题值后的平均值
除此之外,还有特殊格式的信息需要另外处理,比如与时间有关的信息,这里主要分为两部分进行处理:首先是将“连续”的年龄,进行分层处理,即划分年龄段,具体地在这里我们将年龄分为了6个区间。其次是计算具体的年龄,在Excel表格中,只有出生年月以及调查时间等信息,我们根据此计算出每一位调查者的真实年龄。
#144+1 =145
#继续进行特殊的列进行数据处理
#读happiness_index.xlsx
data['survey_time'] = pd.to_datetime(data['survey_time'], format='%Y-%m-%d',errors='coerce')#防止时间格式不同的报错errors='coerce‘
data['survey_time'] = data['survey_time'].dt.year #仅仅是year,方便计算年龄
data['age'] = data['survey_time']-data['birth']
# print(data['age'],data['survey_time'],data['birth'])
#年龄分层 145+1=146
bins = [0,17,26,34,50,63,100]
data['age_bin'] = pd.cut(data['age'], bins, labels=[0,1,2,3,4,5])
在这里因为家庭的收入是连续值,所以不能再使用取众数的方法进行处理,这里就直接使用了均值进行缺失值的补全。第三种方法是使用我们日常生活中的真实情况,例如“宗教信息”特征为负数的认为是“不信仰宗教”,并认为“参加宗教活动的频率”为1,即没有参加过宗教活动,主观的进行补全,这也是我在这一步骤中使用最多的一种方式。
#对‘宗教’处理
data.loc[data['religion']<0,'religion'] = 1 #1为不信仰宗教
data.loc[data['religion_freq']<0,'religion_freq'] = 1 #1为从来没有参加过
#对‘教育程度’处理
data.loc[data['edu']<0,'edu'] = 4 #初中
data.loc[data['edu_status']<0,'edu_status'] = 0
data.loc[data['edu_yr']<0,'edu_yr'] = 0
#对‘个人收入’处理
data.loc[data['income']<0,'income'] = 0 #认为无收入
#对‘政治面貌’处理
data.loc[data['political']<0,'political'] = 1 #认为是群众
#对体重处理
data.loc[(data['weight_jin']<=80)&(data['height_cm']>=160),'weight_jin']= data['weight_jin']*2
data.loc[data['weight_jin']<=60,'weight_jin']= data['weight_jin']*2 #个人的想法,哈哈哈,没有60斤的成年人吧
#对身高处理
data.loc[data['height_cm']<150,'height_cm'] = 150 #成年人的实际情况
#对‘健康’处理
data.loc[data['health']<0,'health'] = 4 #认为是比较健康
data.loc[data['health_problem']<0,'health_problem'] = 4
#对‘沮丧’处理
data.loc[data['depression']<0,'depression'] = 4 #一般人都是很少吧
#对‘媒体’处理
data.loc[data['media_1']<0,'media_1'] = 1 #都是从不
data.loc[data['media_2']<0,'media_2'] = 1
data.loc[data['media_3']<0,'media_3'] = 1
data.loc[data['media_4']<0,'media_4'] = 1
data.loc[data['media_5']<0,'media_5'] = 1
data.loc[data['media_6']<0,'media_6'] = 1
#对‘空闲活动’处理
data.loc[data['leisure_1']<0,'leisure_1'] = 1 #都是根据自己的想法
data.loc[data['leisure_2']<0,'leisure_2'] = 5
data.loc[data['leisure_3']<0,'leisure_3'] = 3
使用众数(代码中使用mode()来实现异常值的修正),由于这里的特征是空闲活动,所以采用众数对于缺失值进行处理比较合理。
data.loc[data['leisure_4']<0,'leisure_4'] = data['leisure_4'].mode() #取众数
data.loc[data['leisure_5']<0,'leisure_5'] = data['leisure_5'].mode()
data.loc[data['leisure_6']<0,'leisure_6'] = data['leisure_6'].mode()
data.loc[data['leisure_7']<0,'leisure_7'] = data['leisure_7'].mode()
data.loc[data['leisure_8']<0,'leisure_8'] = data['leisure_8'].mode()
data.loc[data['leisure_9']<0,'leisure_9'] = data['leisure_9'].mode()
data.loc[data['leisure_10']<0,'leisure_10'] = data['leisure_10'].mode()
data.loc[data['leisure_11']<0,'leisure_11'] = data['leisure_11'].mode()
data.loc[data['leisure_12']<0,'leisure_12'] = data['leisure_12'].mode()
data.loc[data['socialize']<0,'socialize'] = 2 #很少
data.loc[data['relax']<0,'relax'] = 4 #经常
data.loc[data['learn']<0,'learn'] = 1 #从不,哈哈哈哈
#对‘社交’处理
data.loc[data['social_neighbor']<0,'social_neighbor'] = 0
data.loc[data['social_friend']<0,'social_friend'] = 0
data.loc[data['socia_outing']<0,'socia_outing'] = 1
data.loc[data['neighbor_familiarity']<0,'social_neighbor']= 4
#对‘社会公平性’处理
data.loc[data['equity']<0,'equity'] = 4
#对‘社会等级’处理
data.loc[data['class_10_before']<0,'class_10_before'] = 3
data.loc[data['class']<0,'class'] = 5
data.loc[data['class_10_after']<0,'class_10_after'] = 5
data.loc[data['class_14']<0,'class_14'] = 2
#对‘工作情况’处理
data.loc[data['work_status']<0,'work_status'] = 0
data.loc[data['work_yr']<0,'work_yr'] = 0
data.loc[data['work_manage']<0,'work_manage'] = 0
data.loc[data['work_type']<0,'work_type'] = 0
#对‘社会保障’处理
data.loc[data['insur_1']<0,'insur_1'] = 1
data.loc[data['insur_2']<0,'insur_2'] = 1
data.loc[data['insur_3']<0,'insur_3'] = 1
data.loc[data['insur_4']<0,'insur_4'] = 1
data.loc[data['insur_1']==0,'insur_1'] = 0
data.loc[data['insur_2']==0,'insur_2'] = 0
data.loc[data['insur_3']==0,'insur_3'] = 0
data.loc[data['insur_4']==0,'insur_4'] = 0
取均值进行缺失值的补全(代码实现为means()),在这里因为家庭的收入是连续值,所以不能再使用取众数的方法进行处理,这里就直接使用了均值进行缺失值的补全。
#对家庭情况处理
family_income_mean = data['family_income'].mean()
data.loc[data['family_income']<0,'family_income'] = family_income_mean
data.loc[data['family_m']<0,'family_m'] = 2
data.loc[data['family_status']<0,'family_status'] = 3
data.loc[data['house']<0,'house'] = 1
data.loc[data['car']<0,'car'] = 0
data.loc[data['car']==2,'car'] = 0 #变为0和1
data.loc[data['son']<0,'son'] = 1
data.loc[data['daughter']<0,'daughter'] = 0
data.loc[data['minor_child']<0,'minor_child'] = 0
#对‘婚姻’处理
data.loc[data['marital_1st']<0,'marital_1st'] = 0
data.loc[data['marital_now']<0,'marital_now'] = 0
#对‘配偶’处理
data.loc[data['s_birth']<0,'s_birth'] = 0
data.loc[data['s_edu']<0,'s_edu'] = 0
data.loc[data['s_political']<0,'s_political'] = 0
data.loc[data['s_hukou']<0,'s_hukou'] = 0
data.loc[data['s_income']<0,'s_income'] = 0
data.loc[data['s_work_type']<0,'s_work_type'] = 0
data.loc[data['s_work_status']<0,'s_work_status'] = 0
data.loc[data['s_work_exper']<0,'s_work_exper'] = 0
#对‘父母情况’处理
data.loc[data['f_birth']<0,'f_birth'] = 1945
data.loc[data['f_edu']<0,'f_edu'] = 1
data.loc[data['f_political']<0,'f_political'] = 1
data.loc[data['f_work_14']<0,'f_work_14'] = 2
data.loc[data['m_birth']<0,'m_birth'] = 1940
data.loc[data['m_edu']<0,'m_edu'] = 1
data.loc[data['m_political']<0,'m_political'] = 1
data.loc[data['m_work_14']<0,'m_work_14'] = 2
#和同龄人相比社会经济地位
data.loc[data['status_peer']<0,'status_peer'] = 2
#和3年前比社会经济地位
data.loc[data['status_3_before']<0,'status_3_before'] = 2
#对‘观点’处理
data.loc[data['view']<0,'view'] = 4
#对期望年收入处理
data.loc[data['inc_ability']<=0,'inc_ability']= 2
inc_exp_mean = data['inc_exp'].mean()
data.loc[data['inc_exp']<=0,'inc_exp']= inc_exp_mean #取均值
#部分特征处理,取众数(首先去除缺失值的数据)
for i in range(1,9+1):
data.loc[data['public_service_'+str(i)]<0,'public_service_'+str(i)] = data['public_service_'+str(i)].dropna().mode().values
for i in range(1,13+1):
data.loc[data['trust_'+str(i)]<0,'trust_'+str(i)] = data['trust_'+str(i)].dropna().mode().values
数据增广
这一步,我们需要进一步分析每一个特征之间的关系,从而进行数据增广。经过思考,这里我添加了如下的特征:第一次结婚年龄、最近结婚年龄、是否再婚、配偶年龄、配偶年龄差、各种收入比(与配偶之间的收入比、十年后预期收入与现在收入之比等等)、收入与住房面积比(其中也包括10年后期望收入等等各种情况)、社会阶级(10年后的社会阶级、14年后的社会阶级等等)、悠闲指数、满意指数、信任指数等等。除此之外,我还考虑了对于同一省、市、县进行了归一化。例如同一省市内的收入的平均值等以及一个个体相对于同省、市、县其他人的各个指标的情况。同时也考虑了对于同龄人之间的相互比较,即在同龄人中的收入情况、健康情况等等。
#第一次结婚年龄 147
data['marital_1stbir'] = data['marital_1st'] - data['birth']
#最近结婚年龄 148
data['marital_nowtbir'] = data['marital_now'] - data['birth']
#是否再婚 149
data['mar'] = data['marital_nowtbir'] - data['marital_1stbir']
#配偶年龄 150
data['marital_sbir'] = data['marital_now']-data['s_birth']
#配偶年龄差 151
data['age_'] = data['marital_nowtbir'] - data['marital_sbir']
#收入比 151+7 =158
data['income/s_income'] = data['income']/(data['s_income']+1) #同居伴侣
data['income+s_income'] = data['income']+(data['s_income']+1)
data['income/family_income'] = data['income']/(data['family_income']+1)
data['all_income/family_income'] = (data['income']+data['s_income'])/(data['family_income']+1)
data['income/inc_exp'] = data['income']/(data['inc_exp']+1)
data['family_income/m'] = data['family_income']/(data['family_m']+0.01)
data['income/m'] = data['income']/(data['family_m']+0.01)
#收入/面积比 158+4=162
data['income/floor_area'] = data['income']/(data['floor_area']+0.01)
data['all_income/floor_area'] = (data['income']+data['s_income'])/(data['floor_area']+0.01)
data['family_income/floor_area'] = data['family_income']/(data['floor_area']+0.01)
data['floor_area/m'] = data['floor_area']/(data['family_m']+0.01)
#class 162+3=165
data['class_10_diff'] = (data['class_10_after'] - data['class'])
data['class_diff'] = data['class'] - data['class_10_before']
data['class_14_diff'] = data['class'] - data['class_14']
#悠闲指数 166
leisure_fea_lis = ['leisure_'+str(i) for i in range(1,13)]
data['leisure_sum'] = data[leisure_fea_lis].sum(axis=1) #skew
#满意指数 167
public_service_fea_lis = ['public_service_'+str(i) for i in range(1,10)]
data['public_service_sum'] = data[public_service_fea_lis].sum(axis=1) #skew
#信任指数 168
trust_fea_lis = ['trust_'+str(i) for i in range(1,14)]
data['trust_sum'] = data[trust_fea_lis].sum(axis=1) #skew
#province mean 168+13=181
data['province_income_mean'] = data.groupby(['province'])['income'].transform('mean').values
data['province_family_income_mean'] = data.groupby(['province'])['family_income'].transform('mean').values
data['province_equity_mean'] = data.groupby(['province'])['equity'].transform('mean').values
data['province_depression_mean'] = data.groupby(['province'])['depression'].transform('mean').values
data['province_floor_area_mean'] = data.groupby(['province'])['floor_area'].transform('mean').values
data['province_health_mean'] = data.groupby(['province'])['health'].transform('mean').values
data['province_class_10_diff_mean'] = data.groupby(['province'])['class_10_diff'].transform('mean').values
data['province_class_mean'] = data.groupby(['province'])['class'].transform('mean').values
data['province_health_problem_mean'] = data.groupby(['province'])['health_problem'].transform('mean').values
data['province_family_status_mean'] = data.groupby(['province'])['family_status'].transform('mean').values
data['province_leisure_sum_mean'] = data.groupby(['province'])['leisure_sum'].transform('mean').values
data['province_public_service_sum_mean'] = data.groupby(['province'])['public_service_sum'].transform('mean').values
data['province_trust_sum_mean'] = data.groupby(['province'])['trust_sum'].transform('mean').values
#city mean 181+13=194
data['city_income_mean'] = data.groupby(['city'])['income'].transform('mean').values #按照city分组
data['city_family_income_mean'] = data.groupby(['city'])['family_income'].transform('mean').values
data['city_equity_mean'] = data.groupby(['city'])['equity'].transform('mean').values
data['city_depression_mean'] = data.groupby(['city'])['depression'].transform('mean').values
data['city_floor_area_mean'] = data.groupby(['city'])['floor_area'].transform('mean').values
data['city_health_mean'] = data.groupby(['city'])['health'].transform('mean').values
data['city_class_10_diff_mean'] = data.groupby(['city'])['class_10_diff'].transform('mean').values
data['city_class_mean'] = data.groupby(['city'])['class'].transform('mean').values
data['city_health_problem_mean'] = data.groupby(['city'])['health_problem'].transform('mean').values
data['city_family_status_mean'] = data.groupby(['city'])['family_status'].transform('mean').values
data['city_leisure_sum_mean'] = data.groupby(['city'])['leisure_sum'].transform('mean').values
data['city_public_service_sum_mean'] = data.groupby(['city'])['public_service_sum'].transform('mean').values
data['city_trust_sum_mean'] = data.groupby(['city'])['trust_sum'].transform('mean').values
#county mean 194 + 13 = 207
data['county_income_mean'] = data.groupby(['county'])['income'].transform('mean').values
data['county_family_income_mean'] = data.groupby(['county'])['family_income'].transform('mean').values
data['county_equity_mean'] = data.groupby(['county'])['equity'].transform('mean').values
data['county_depression_mean'] = data.groupby(['county'])['depression'].transform('mean').values
data['county_floor_area_mean'] = data.groupby(['county'])['floor_area'].transform('mean').values
data['county_health_mean'] = data.groupby(['county'])['health'].transform('mean').values
data['county_class_10_diff_mean'] = data.groupby(['county'])['class_10_diff'].transform('mean').values
data['county_class_mean'] = data.groupby(['county'])['class'].transform('mean').values
data['county_health_problem_mean'] = data.groupby(['county'])['health_problem'].transform('mean').values
data['county_family_status_mean'] = data.groupby(['county'])['family_status'].transform('mean').values
data['county_leisure_sum_mean'] = data.groupby(['county'])['leisure_sum'].transform('mean').values
data['county_public_service_sum_mean'] = data.groupby(['county'])['public_service_sum'].transform('mean').values
data['county_trust_sum_mean'] = data.groupby(['county'])['trust_sum'].transform('mean').values
#ratio 相比同省 207 + 13 =220
data['income/province'] = data['income']/(data['province_income_mean'])
data['family_income/province'] = data['family_income']/(data['province_family_income_mean'])
data['equity/province'] = data['equity']/(data['province_equity_mean'])
data['depression/province'] = data['depression']/(data['province_depression_mean'])
data['floor_area/province'] = data['floor_area']/(data['province_floor_area_mean'])
data['health/province'] = data['health']/(data['province_health_mean'])
data['class_10_diff/province'] = data['class_10_diff']/(data['province_class_10_diff_mean'])
data['class/province'] = data['class']/(data['province_class_mean'])
data['health_problem/province'] = data['health_problem']/(data['province_health_problem_mean'])
data['family_status/province'] = data['family_status']/(data['province_family_status_mean'])
data['leisure_sum/province'] = data['leisure_sum']/(data['province_leisure_sum_mean'])
data['public_service_sum/province'] = data['public_service_sum']/(data['province_public_service_sum_mean'])
data['trust_sum/province'] = data['trust_sum']/(data['province_trust_sum_mean']+1)
#ratio 相比同市 220 + 13 =233
data['income/city'] = data['income']/(data['city_income_mean'])
data['family_income/city'] = data['family_income']/(data['city_family_income_mean'])
data['equity/city'] = data['equity']/(data['city_equity_mean'])
data['depression/city'] = data['depression']/(data['city_depression_mean'])
data['floor_area/city'] = data['floor_area']/(data['city_floor_area_mean'])
data['health/city'] = data['health']/(data['city_health_mean'])
data['class_10_diff/city'] = data['class_10_diff']/(data['city_class_10_diff_mean'])
data['class/city'] = data['class']/(data['city_class_mean'])
data['health_problem/city'] = data['health_problem']/(data['city_health_problem_mean'])
data['family_status/city'] = data['family_status']/(data['city_family_status_mean'])
data['leisure_sum/city'] = data['leisure_sum']/(data['city_leisure_sum_mean'])
data['public_service_sum/city'] = data['public_service_sum']/(data['city_public_service_sum_mean'])
data['trust_sum/city'] = data['trust_sum']/(data['city_trust_sum_mean'])
#ratio 相比同个地区 233 + 13 =246
data['income/county'] = data['income']/(data['county_income_mean'])
data['family_income/county'] = data['family_income']/(data['county_family_income_mean'])
data['equity/county'] = data['equity']/(data['county_equity_mean'])
data['depression/county'] = data['depression']/(data['county_depression_mean'])
data['floor_area/county'] = data['floor_area']/(data['county_floor_area_mean'])
data['health/county'] = data['health']/(data['county_health_mean'])
data['class_10_diff/county'] = data['class_10_diff']/(data['county_class_10_diff_mean'])
data['class/county'] = data['class']/(data['county_class_mean'])
data['health_problem/county'] = data['health_problem']/(data['county_health_problem_mean'])
data['family_status/county'] = data['family_status']/(data['county_family_status_mean'])
data['leisure_sum/county'] = data['leisure_sum']/(data['county_leisure_sum_mean'])
data['public_service_sum/county'] = data['public_service_sum']/(data['county_public_service_sum_mean'])
data['trust_sum/county'] = data['trust_sum']/(data['county_trust_sum_mean'])
#age mean 246+ 13 =259
data['age_income_mean'] = data.groupby(['age'])['income'].transform('mean').values
data['age_family_income_mean'] = data.groupby(['age'])['family_income'].transform('mean').values
data['age_equity_mean'] = data.groupby(['age'])['equity'].transform('mean').values
data['age_depression_mean'] = data.groupby(['age'])['depression'].transform('mean').values
data['age_floor_area_mean'] = data.groupby(['age'])['floor_area'].transform('mean').values
data['age_health_mean'] = data.groupby(['age'])['health'].transform('mean').values
data['age_class_10_diff_mean'] = data.groupby(['age'])['class_10_diff'].transform('mean').values
data['age_class_mean'] = data.groupby(['age'])['class'].transform('mean').values
data['age_health_problem_mean'] = data.groupby(['age'])['health_problem'].transform('mean').values
data['age_family_status_mean'] = data.groupby(['age'])['family_status'].transform('mean').values
data['age_leisure_sum_mean'] = data.groupby(['age'])['leisure_sum'].transform('mean').values
data['age_public_service_sum_mean'] = data.groupby(['age'])['public_service_sum'].transform('mean').values
data['age_trust_sum_mean'] = data.groupby(['age'])['trust_sum'].transform('mean').values
# 和同龄人相比259 + 13 =272
data['income/age'] = data['income']/(data['age_income_mean'])
data['family_income/age'] = data['family_income']/(data['age_family_income_mean'])
data['equity/age'] = data['equity']/(data['age_equity_mean'])
data['depression/age'] = data['depression']/(data['age_depression_mean'])
data['floor_area/age'] = data['floor_area']/(data['age_floor_area_mean'])
data['health/age'] = data['health']/(data['age_health_mean'])
data['class_10_diff/age'] = data['class_10_diff']/(data['age_class_10_diff_mean'])
data['class/age'] = data['class']/(data['age_class_mean'])
data['health_problem/age'] = data['health_problem']/(data['age_health_problem_mean'])
data['family_status/age'] = data['family_status']/(data['age_family_status_mean'])
data['leisure_sum/age'] = data['leisure_sum']/(data['age_leisure_sum_mean'])
data['public_service_sum/age'] = data['public_service_sum']/(data['age_public_service_sum_mean'])
data['trust_sum/age'] = data['trust_sum']/(data['age_trust_sum_mean'])
经过如上的操作后,最终我们的特征从一开始的131维,扩充为了272维的特征。接下来考虑特征工程、训练模型以及模型融合的工作。
print('shape',data.shape)
data.head()
还应该删去有效样本数很少的特征,例如负值太多的特征或者是缺失值太多的特征,这里我一共删除了包括“目前的最高教育程度”在内的9类特征,得到了最终的263维的特征。
#272-9=263
#删除数值特别少的和之前用过的特征
del_list=['id','survey_time','edu_other','invest_other','property_other','join_party','province','city','county']
use_feature = [clo for clo in data.columns if clo not in del_list]
data.fillna(0,inplace=True) #还是补0
train_shape = train.shape[0] #一共的数据量,训练集
features = data[use_feature].columns #删除后所有的特征
X_train_263 = data[:train_shape][use_feature].values
y_train = target
X_test_263 = data[train_shape:][use_feature].values
X_train_263.shape #最终一种263个特征
选择了最重要的49个特征,作为除了以上263维特征外的另外一组特征。
imp_fea_49 = ['equity','depression','health','class','family_status','health_problem','class_10_after',
'equity/province','equity/city','equity/county',
'depression/province','depression/city','depression/county',
'health/province','health/city','health/county',
'class/province','class/city','class/county',
'family_status/province','family_status/city','family_status/county',
'family_income/province','family_income/city','family_income/county',
'floor_area/province','floor_area/city','floor_area/county',
'leisure_sum/province','leisure_sum/city','leisure_sum/county',
'public_service_sum/province','public_service_sum/city','public_service_sum/county',
'trust_sum/province','trust_sum/city','trust_sum/county',
'income/m','public_service_sum','class_diff','status_3_before','age_income_mean','age_floor_area_mean',
'weight_jin','height_cm',
'health/age','depression/age','equity/age','leisure_sum/age'
]
train_shape = train.shape[0]
X_train_49 = data[:train_shape][imp_fea_49].values
X_test_49 = data[train_shape:][imp_fea_49].values
X_train_49.shape #最重要的49个特征
选择需要进行onehot编码的离散变量进行one-hot编码,再合成为第三类特征,共383维。
cat_fea = ['survey_type','gender','nationality','edu_status','political','hukou','hukou_loc','work_exper','work_status','work_type',
'work_manage','marital','s_political','s_hukou','s_work_exper','s_work_status','s_work_type','f_political','f_work_14',
'm_political','m_work_14'] #已经是0、1的值不需要onehot
noc_fea = [clo for clo in use_feature if clo not in cat_fea]
onehot_data = data[cat_fea].values
enc = preprocessing.OneHotEncoder(categories = 'auto')
oh_data=enc.fit_transform(onehot_data).toarray()
oh_data.shape #变为onehot编码格式
X_train_oh = oh_data[:train_shape,:]
X_test_oh = oh_data[train_shape:,:]
X_train_oh.shape #其中的训练集
X_train_383 = np.column_stack([data[:train_shape][noc_fea].values,X_train_oh])#先是noc,再是cat_fea
X_test_383 = np.column_stack([data[train_shape:][noc_fea].values,X_test_oh])
X_train_383.shape
基于此,我们构建完成了三种特征工程(训练数据集),其一是上面提取的最重要的49中特征,其中包括健康程度、社会阶级、在同龄人中的收入情况等等特征。其二是扩充后的263维特征(这里可以认为是初始特征)。其三是使用One-hot编码后的特征,这里要使用One-hot进行编码的原因在于,有部分特征为分离值,例如性别中男女,男为1,女为2,我们想使用One-hot将其变为男为0,女为1,来增强机器学习算法的鲁棒性能;再如民族这个特征,原本是1-56这56个数值,如果直接分类会让分类器的鲁棒性变差,所以使用One-hot编码将其变为6个特征进行非零即一的处理。
特征建模
首先我们对于原始的263维的特征,使用lightGBM进行处理,这里我们使用5折交叉验证的方法:
1、lightGBM
##### lgb_263 #
#lightGBM决策树
lgb_263_param = {
'num_leaves': 7,
'min_data_in_leaf': 20, #叶子可能具有的最小记录数
'objective':'regression',
'max_depth': -1,
'learning_rate': 0.003,
"boosting": "gbdt", #用gbdt算法
"feature_fraction": 0.18, #例如 0.18时,意味着在每次迭代中随机选择18%的参数来建树
"bagging_freq": 1,
"bagging_fraction": 0.55, #每次迭代时用的数据比例
"bagging_seed": 14,
"metric": 'mse',
"lambda_l1": 0.1,
"lambda_l2": 0.2,
"verbosity": -1}
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=4) #交叉切分:5
oof_lgb_263 = np.zeros(len(X_train_263))
predictions_lgb_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print("fold n°{}".format(fold_+1))
trn_data = lgb.Dataset(X_train_263[trn_idx], y_train[trn_idx])
val_data = lgb.Dataset(X_train_263[val_idx], y_train[val_idx])#train:val=4:1
num_round = 10000
lgb_263 = lgb.train(lgb_263_param, trn_data, num_round, valid_sets = [trn_data, val_data], verbose_eval=500, early_stopping_rounds = 800)
oof_lgb_263[val_idx] = lgb_263.predict(X_train_263[val_idx], num_iteration=lgb_263.best_iteration)
predictions_lgb_263 += lgb_263.predict(X_test_263, num_iteration=lgb_263.best_iteration) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_lgb_263, target)))
接着,我使用已经训练完的lightGBM的模型进行特征重要性的判断以及可视化,从结果我们可以看出,排在重要性第一位的是health/age,就是同龄人中的健康程度,与我们主观的看法基本一致。
#---------------特征重要性
pd.set_option('display.max_columns', None)
#显示所有行
pd.set_option('display.max_rows', None)
#设置value的显示长度为100,默认为50
pd.set_option('max_colwidth',100)
df = pd.DataFrame(data[use_feature].columns.tolist(), columns=['feature'])
df['importance']=list(lgb_263.feature_importance())
df = df.sort_values(by='importance',ascending=False)
plt.figure(figsize=(14,28))
sns.barplot(x="importance", y="feature", data=df.head(50))
plt.title('Features importance (averaged/folds)')
plt.tight_layout()
后面,我们使用常见的机器学习方法,对于263维特征进行建模:
2、XGboost
##### xgb_263
#xgboost
xgb_263_params = {'eta': 0.02, #lr
'max_depth': 6,
'min_child_weight':3,#最小叶子节点样本权重和
'gamma':0, #指定节点分裂所需的最小损失函数下降值。
'subsample': 0.7, #控制对于每棵树,随机采样的比例
'colsample_bytree': 0.3, #用来控制每棵随机采样的列数的占比 (每一列是一个特征)。
'lambda':2,
'objective': 'reg:linear',
'eval_metric': 'rmse',
'silent': True,
'nthread': -1}
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2019)
oof_xgb_263 = np.zeros(len(X_train_263))
predictions_xgb_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print("fold n°{}".format(fold_+1))
trn_data = xgb.DMatrix(X_train_263[trn_idx], y_train[trn_idx])
val_data = xgb.DMatrix(X_train_263[val_idx], y_train[val_idx])
watchlist = [(trn_data, 'train'), (val_data, 'valid_data')]
xgb_263 = xgb.train(dtrain=trn_data, num_boost_round=3000, evals=watchlist, early_stopping_rounds=600, verbose_eval=500, params=xgb_263_params)
oof_xgb_263[val_idx] = xgb_263.predict(xgb.DMatrix(X_train_263[val_idx]), ntree_limit=xgb_263.best_ntree_limit)
predictions_xgb_263 += xgb_263.predict(xgb.DMatrix(X_test_263), ntree_limit=xgb_263.best_ntree_limit) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_xgb_263, target)))
3、RandomForestRegressor随机森林
#RandomForestRegressor随机森林
folds = KFold(n_splits=5, shuffle=True, random_state=2019)
oof_rfr_263 = np.zeros(len(X_train_263))
predictions_rfr_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_263[trn_idx]
tr_y = y_train[trn_idx]
rfr_263 = rfr(n_estimators=1600,max_depth=9, min_samples_leaf=9, min_weight_fraction_leaf=0.0,
max_features=0.25,verbose=1,n_jobs=-1) #并行化
#verbose = 0 为不在标准输出流输出日志信息
#verbose = 1 为输出进度条记录
#verbose = 2 为每个epoch输出一行记录
rfr_263.fit(tr_x,tr_y)
oof_rfr_263[val_idx] = rfr_263.predict(X_train_263[val_idx])
predictions_rfr_263 += rfr_263.predict(X_test_263) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_rfr_263, target)))
4、GradientBoostingRegressor梯度提升决策树
#GradientBoostingRegressor梯度提升决策树
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2018)
oof_gbr_263 = np.zeros(train_shape)
predictions_gbr_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_263[trn_idx]
tr_y = y_train[trn_idx]
gbr_263 = gbr(n_estimators=400, learning_rate=0.01,subsample=0.65,max_depth=7, min_samples_leaf=20,
max_features=0.22,verbose=1)
gbr_263.fit(tr_x,tr_y)
oof_gbr_263[val_idx] = gbr_263.predict(X_train_263[val_idx])
predictions_gbr_263 += gbr_263.predict(X_test_263) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_gbr_263, target)))
5、ExtraTreesRegressor 极端随机森林回归
#ExtraTreesRegressor 极端随机森林回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_etr_263 = np.zeros(train_shape)
predictions_etr_263 = np.zeros(len(X_test_263))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_263, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_263[trn_idx]
tr_y = y_train[trn_idx]
etr_263 = etr(n_estimators=1000,max_depth=8, min_samples_leaf=12, min_weight_fraction_leaf=0.0,
max_features=0.4,verbose=1,n_jobs=-1)# max_feature:划分时考虑的最大特征数
etr_263.fit(tr_x,tr_y)
oof_etr_263[val_idx] = etr_263.predict(X_train_263[val_idx])
predictions_etr_263 += etr_263.predict(X_test_263) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_etr_263, target)))
至此,我们得到了以上5种模型的预测结果以及模型架构及参数。其中在每一种特征工程中,进行5折的交叉验证,并重复两次(Kernel Ridge Regression,核脊回归),取得每一个特征数下的模型的结果。
train_stack2 = np.vstack([oof_lgb_263,oof_xgb_263,oof_gbr_263,oof_rfr_263,oof_etr_263]).transpose()
# transpose()函数的作用就是调换x,y,z的位置,也就是数组的索引值
test_stack2 = np.vstack([predictions_lgb_263, predictions_xgb_263,predictions_gbr_263,predictions_rfr_263,predictions_etr_263]).transpose()
#交叉验证:5折,重复2次
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack2 = np.zeros(train_stack2.shape[0])
predictions_lr2 = np.zeros(test_stack2.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack2,target)):
print("fold {}".format(fold_))
trn_data, trn_y = train_stack2[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack2[val_idx], target.iloc[val_idx].values
#Kernel Ridge Regression
lr2 = kr()
lr2.fit(trn_data, trn_y)
oof_stack2[val_idx] = lr2.predict(val_data)
predictions_lr2 += lr2.predict(test_stack2) / 10
mean_squared_error(target.values, oof_stack2)
接下来我们对于49维的数据进行与上述263维数据相同的操作。
1、LightGBM
##### lgb_49
lgb_49_param = {
'num_leaves': 9,
'min_data_in_leaf': 23,
'objective':'regression',
'max_depth': -1,
'learning_rate': 0.002,
"boosting": "gbdt",
"feature_fraction": 0.45,
"bagging_freq": 1,
"bagging_fraction": 0.65,
"bagging_seed": 15,
"metric": 'mse',
"lambda_l2": 0.2,
"verbosity": -1} # 一个叶子上数据的最小数量 \ feature_fraction将会在每棵树训练之前选择 45% 的特征。可以用来加速训练,可以用来处理过拟合。 #bagging_fraction不进行重采样的情况下随机选择部分数据。可以用来加速训练,可以用来处理过拟合。
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=9)
oof_lgb_49 = np.zeros(len(X_train_49))
predictions_lgb_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print("fold n°{}".format(fold_+1))
trn_data = lgb.Dataset(X_train_49[trn_idx], y_train[trn_idx])
val_data = lgb.Dataset(X_train_49[val_idx], y_train[val_idx])
num_round = 12000
lgb_49 = lgb.train(lgb_49_param, trn_data, num_round, valid_sets = [trn_data, val_data], verbose_eval=1000, early_stopping_rounds = 1000)
oof_lgb_49[val_idx] = lgb_49.predict(X_train_49[val_idx], num_iteration=lgb_49.best_iteration)
predictions_lgb_49 += lgb_49.predict(X_test_49, num_iteration=lgb_49.best_iteration) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_lgb_49, target)))
2、XGBoost
##### xgb_49
xgb_49_params = {'eta': 0.02,
'max_depth': 5,
'min_child_weight':3,
'gamma':0,
'subsample': 0.7,
'colsample_bytree': 0.35,
'lambda':2,
'objective': 'reg:linear',
'eval_metric': 'rmse',
'silent': True,
'nthread': -1}
folds = KFold(n_splits=5, shuffle=True, random_state=2019)
oof_xgb_49 = np.zeros(len(X_train_49))
predictions_xgb_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print("fold n°{}".format(fold_+1))
trn_data = xgb.DMatrix(X_train_49[trn_idx], y_train[trn_idx])
val_data = xgb.DMatrix(X_train_49[val_idx], y_train[val_idx])
watchlist = [(trn_data, 'train'), (val_data, 'valid_data')]
xgb_49 = xgb.train(dtrain=trn_data, num_boost_round=3000, evals=watchlist, early_stopping_rounds=600, verbose_eval=500, params=xgb_49_params)
oof_xgb_49[val_idx] = xgb_49.predict(xgb.DMatrix(X_train_49[val_idx]), ntree_limit=xgb_49.best_ntree_limit)
predictions_xgb_49 += xgb_49.predict(xgb.DMatrix(X_test_49), ntree_limit=xgb_49.best_ntree_limit) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_xgb_49, target)))
3、GradientBoostingRegressor梯度提升决策树
folds = StratifiedKFold(n_splits=5, shuffle=True, random_state=2018)
oof_gbr_49 = np.zeros(train_shape)
predictions_gbr_49 = np.zeros(len(X_test_49))
#GradientBoostingRegressor梯度提升决策树
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
gbr_49 = gbr(n_estimators=600, learning_rate=0.01,subsample=0.65,max_depth=6, min_samples_leaf=20,
max_features=0.35,verbose=1)
gbr_49.fit(tr_x,tr_y)
oof_gbr_49[val_idx] = gbr_49.predict(X_train_49[val_idx])
predictions_gbr_49 += gbr_49.predict(X_test_49) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_gbr_49, target)))
至此,我们得到了以上3种模型的基于49个特征的预测结果以及模型架构及参数。其中在每一种特征工程中,进行5折的交叉验证,并重复两次(Kernel Ridge Regression,核脊回归),取得每一个特征数下的模型的结果。
train_stack3 = np.vstack([oof_lgb_49,oof_xgb_49,oof_gbr_49]).transpose()
test_stack3 = np.vstack([predictions_lgb_49, predictions_xgb_49,predictions_gbr_49]).transpose()
#
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack3 = np.zeros(train_stack3.shape[0])
predictions_lr3 = np.zeros(test_stack3.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack3,target)):
print("fold {}".format(fold_))
trn_data, trn_y = train_stack3[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack3[val_idx], target.iloc[val_idx].values
#Kernel Ridge Regression
lr3 = kr()
lr3.fit(trn_data, trn_y)
oof_stack3[val_idx] = lr3.predict(val_data)
predictions_lr3 += lr3.predict(test_stack3) / 10
mean_squared_error(target.values, oof_stack3)
接下来我们对于383维的数据进行与上述263以及49维数据相同的操作。
1、Kernel Ridge Regression 基于核的岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_kr_383 = np.zeros(train_shape)
predictions_kr_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#Kernel Ridge Regression 岭回归
kr_383 = kr()
kr_383.fit(tr_x,tr_y)
oof_kr_383[val_idx] = kr_383.predict(X_train_383[val_idx])
predictions_kr_383 += kr_383.predict(X_test_383) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_kr_383, target)))
2、使用普通岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_ridge_383 = np.zeros(train_shape)
predictions_ridge_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#使用岭回归
ridge_383 = Ridge(alpha=1200)
ridge_383.fit(tr_x,tr_y)
oof_ridge_383[val_idx] = ridge_383.predict(X_train_383[val_idx])
predictions_ridge_383 += ridge_383.predict(X_test_383) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_ridge_383, target)))
3、使用ElasticNet 弹性网络
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_en_383 = np.zeros(train_shape)
predictions_en_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#ElasticNet 弹性网络
en_383 = en(alpha=1.0,l1_ratio=0.06)
en_383.fit(tr_x,tr_y)
oof_en_383[val_idx] = en_383.predict(X_train_383[val_idx])
predictions_en_383 += en_383.predict(X_test_383) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_en_383, target)))
4、使用BayesianRidge 贝叶斯岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_br_383 = np.zeros(train_shape)
predictions_br_383 = np.zeros(len(X_test_383))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_383, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_383[trn_idx]
tr_y = y_train[trn_idx]
#BayesianRidge 贝叶斯回归
br_383 = br()
br_383.fit(tr_x,tr_y)
oof_br_383[val_idx] = br_383.predict(X_train_383[val_idx])
predictions_br_383 += br_383.predict(X_test_383) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_br_383, target)))
至此,我们得到了以上4种模型的基于383个特征的预测结果以及模型架构及参数。其中在每一种特征工程中,进行5折的交叉验证,并重复两次(LinearRegression简单的线性回归),取得每一个特征数下的模型的结果。
train_stack1 = np.vstack([oof_br_383,oof_kr_383,oof_en_383,oof_ridge_383]).transpose()
test_stack1 = np.vstack([predictions_br_383, predictions_kr_383,predictions_en_383,predictions_ridge_383]).transpose()
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack1 = np.zeros(train_stack1.shape[0])
predictions_lr1 = np.zeros(test_stack1.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack1,target)):
print("fold {}".format(fold_))
trn_data, trn_y = train_stack1[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack1[val_idx], target.iloc[val_idx].values
# LinearRegression简单的线性回归
lr1 = lr()
lr1.fit(trn_data, trn_y)
oof_stack1[val_idx] = lr1.predict(val_data)
predictions_lr1 += lr1.predict(test_stack1) / 10
mean_squared_error(target.values, oof_stack1)
由于49维的特征是最重要的特征,所以这里考虑增加更多的模型进行49维特征的数据的构建工作。
1、KernelRidge 核岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_kr_49 = np.zeros(train_shape)
predictions_kr_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
kr_49 = kr()
kr_49.fit(tr_x,tr_y)
oof_kr_49[val_idx] = kr_49.predict(X_train_49[val_idx])
predictions_kr_49 += kr_49.predict(X_test_49) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_kr_49, target)))
2、Ridge 岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_ridge_49 = np.zeros(train_shape)
predictions_ridge_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
ridge_49 = Ridge(alpha=6)
ridge_49.fit(tr_x,tr_y)
oof_ridge_49[val_idx] = ridge_49.predict(X_train_49[val_idx])
predictions_ridge_49 += ridge_49.predict(X_test_49) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_ridge_49, target)))
3、BayesianRidge 贝叶斯岭回归
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_br_49 = np.zeros(train_shape)
predictions_br_49 = np.zeros(len(X_test_49))
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
br_49 = br()
br_49.fit(tr_x,tr_y)
oof_br_49[val_idx] = br_49.predict(X_train_49[val_idx])
predictions_br_49 += br_49.predict(X_test_49) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_br_49, target)))
4、ElasticNet 弹性网络
folds = KFold(n_splits=5, shuffle=True, random_state=13)
oof_en_49 = np.zeros(train_shape)
predictions_en_49 = np.zeros(len(X_test_49))
#
for fold_, (trn_idx, val_idx) in enumerate(folds.split(X_train_49, y_train)):
print("fold n°{}".format(fold_+1))
tr_x = X_train_49[trn_idx]
tr_y = y_train[trn_idx]
en_49 = en(alpha=1.0,l1_ratio=0.05)
en_49.fit(tr_x,tr_y)
oof_en_49[val_idx] = en_49.predict(X_train_49[val_idx])
predictions_en_49 += en_49.predict(X_test_49) / folds.n_splits
print("CV score: {:<8.8f}".format(mean_squared_error(oof_en_49, target)))
我们得到了以上4种新模型的基于49个特征的预测结果以及模型架构及参数。其中在每一种特征工程中,进行5折的交叉验证,并重复两次(LinearRegression简单的线性回归),取得每一个特征数下的模型的结果。
train_stack4 = np.vstack([oof_br_49,oof_kr_49,oof_en_49,oof_ridge_49]).transpose()
test_stack4 = np.vstack([predictions_br_49, predictions_kr_49,predictions_en_49,predictions_ridge_49]).transpose()
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack4 = np.zeros(train_stack4.shape[0])
predictions_lr4 = np.zeros(test_stack4.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack4,target)):
print("fold {}".format(fold_))
trn_data, trn_y = train_stack4[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack4[val_idx], target.iloc[val_idx].values
#LinearRegression
lr4 = lr()
lr4.fit(trn_data, trn_y)
oof_stack4[val_idx] = lr4.predict(val_data)
predictions_lr4 += lr4.predict(test_stack1) / 10
mean_squared_error(target.values, oof_stack4)
模型融合
这里对于上述四种集成学习的模型的预测结果进行加权的求和,得到最终的结果,当然这种方式是很不准确的。
#和下面作对比
mean_squared_error(target.values, 0.7*(0.6*oof_stack2 + 0.4*oof_stack3)+0.3*(0.55*oof_stack1+0.45*oof_stack4))
更好的方式是将以上的4中集成学习模型再次进行集成学习的训练,这里直接使用LinearRegression简单线性回归的进行集成。
train_stack5 = np.vstack([oof_stack1,oof_stack2,oof_stack3,oof_stack4]).transpose()
test_stack5 = np.vstack([predictions_lr1, predictions_lr2,predictions_lr3,predictions_lr4]).transpose()
folds_stack = RepeatedKFold(n_splits=5, n_repeats=2, random_state=7)
oof_stack5 = np.zeros(train_stack5.shape[0])
predictions_lr5= np.zeros(test_stack5.shape[0])
for fold_, (trn_idx, val_idx) in enumerate(folds_stack.split(train_stack5,target)):
print("fold {}".format(fold_))
trn_data, trn_y = train_stack5[trn_idx], target.iloc[trn_idx].values
val_data, val_y = train_stack5[val_idx], target.iloc[val_idx].values
#LinearRegression
lr5 = lr()
lr5.fit(trn_data, trn_y)
oof_stack5[val_idx] = lr5.predict(val_data)
predictions_lr5 += lr5.predict(test_stack5) / 10
mean_squared_error(target.values, oof_stack5)
结果保存
进行index的读取工作。
submit_example = pd.read_csv('submit_example.csv',sep=',',encoding='latin-1')
submit_example['happiness'] = predictions_lr5
submit_example.happiness.describe()
进行结果保存,这里我们预测出的值是1-5的连续值,但是我们的ground truth是整数值,所以为了进一步优化我们的结果,我们对于结果进行了整数解的近似,并保存到了csv文件中。
submit_example.loc[submit_example['happiness']>4.96,'happiness']= 5
submit_example.loc[submit_example['happiness']<=1.04,'happiness']= 1
submit_example.loc[(submit_example['happiness']>1.96)&(submit_example['happiness']<2.04),'happiness']= 2
submit_example.to_csv("submision.csv",index=False)
submit_example.happiness.describe()
可以对于model的参数进行更进一步的调整,例如使用网格搜索的方法。
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
iris = load_iris()
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=0)
print("Size of training set:{} size of testing set:{}".format(X_train.shape[0],X_test.shape[0]))
#### 1
best_score = 0
for gamma in [0.001,0.01,0.1,1,10,100]:
for C in [0.001,0.01,0.1,1,10,100]:
svm = SVC(gamma=gamma,C=C)#对于每种参数可能的组合,进行一次训练;
svm.fit(X_train,y_train)
score = svm.score(X_test,y_test)
if score > best_score:#找到表现最好的参数
best_score = score
best_parameters = {'gamma':gamma,'C':C}
print("Best score:{:.2f}".format(best_score))
#### 2
from sklearn.model_selection import GridSearchCV
#把要调整的参数以及其候选值 列出来;
param_grid = {"gamma":[0.001,0.01,0.1,1,10,100],
"C":[0.001,0.01,0.1,1,10,100]}
print("Parameters:{}".format(param_grid))
grid_search = GridSearchCV(SVC(),param_grid,cv=5) #实例化一个GridSearchCV类,cv交叉验证参数
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=10)
grid_search.fit(X_train,y_train) #训练,找到最优的参数,同时使用最优的参数实例化一个新的SVC estimator。
print("Test set score:{:.2f}".format(grid_search.score(X_test,y_test)))
print("Best parameters:{}".format(grid_search.best_params_))
#SVM模型有两个非常重要的参数C与gamma。
#C是惩罚系数,即对误差的容忍度(间隔大小,分类准确度)。C越高,说明越不能容忍出现误差,容易过拟合。C越小,容易欠拟合。C过大或过小,泛化能力变差
#gamma是选择RBF函数作为kernel后,该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布,gamma越大,支持向量越少,gamma值越小,支持向量越多。支持向量的个数影响训练与预测的速度。
#两者独立
#Grid Search 调参方法存在的共性弊端就是:耗时;参数越多,候选值越多,耗费时间越长!所以,一般情况下,先定一个大范围,然后再细化。