一、RNN循环神经网络

1.RNN的背景

RNN循环神经网络是在自然语言处理中常见的处理工具和手段
不知道大家通过学习了解了普通的神经网络之后再来接触RNN会不会有一个疑问，就是感觉RNN不就是一般的神经网络套上一个循环吗，有必要还专门研究出一个东西叫做RNN吗？我在一开始接触的时候也百思不得其解~
但其实一般的神经网络模型都只能单独的去处理一个个的输入，前、后的输入之间是完全没有联系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。就像我们人平时讲话一样，一个一个字地去看虽然仍然可以看得懂字，但想要理解全文的意思就需要把上下文的语句联系起来，这也就是RNN存在的意义。
举例：
1.假设现在有一条语句 $“我\ 吃\ 苹果”$ 我们的任务是要对“我\ 吃\ 苹果”这一语句进行词性标注
2.如果我们使用一般的神经网络模型，那我们要做的就是向向模型中输入“我”，然后得到标出好的词性“nn”或者说“我/nn”。
3.但通过我们日常的经验可以知道，我们中文的使用的时候，如果前一个词是名词的的话，那么下一个词是动词的概率应该会远远大于下一个词是名词的概率。就像本例中的“我”这一名词后面紧跟的就是“吃”这一动词，这也就说明了一个句子中，前一个单词其实对于当前单词的词性预测是有很大影响的。然而一般神经网络模型却并没有考虑到这一点。
4.所以RNN的出现就弥补了传统神经网络模型在这一方面的不足，处理序列的时候在信息节点之间建立起了联系。

2.RNN的结构

我们先来看看传统的神经网络模型吧

正如我们前面提到的那样传统的神经网络模型并没有将前、后的输入信息联系起来。
再来看看RNN循环神经网络的结构

可以很明显的看出来RNN循环神经网络的结构与传统的神经网络模型的区别吧，就是在处理序列的时候将信息节点之间建立起了联系（图中的红色箭头），或许这样一张图看着可能有些吓人，难以理解，但我摆出这两张图的目的就是为了让大家有一个对比，能够看到RNN循环神经网络的结构与传统的神经网络模型的区别到底体现在哪里。
下面为了帮助理解，我们下列更加具体的介绍：

这是一个简单的循环神经网络如，它由输入层、一个隐藏层和一个输出层组成。
X是一个向量，它表示输入层的值，S是一个向量，它表示隐藏层的值（这里隐藏层面只画了一个节点，但其实隐藏层一般是多个节点），U是输入层到隐藏层的权重矩阵，O也是一个向量，它表示输出层的值，V是隐藏层到输出层的权重矩阵。
那么，现在我们来看看W是什么？循环神经网络的隐藏层的值S不仅仅取决于当前这次的输入X，还取决于上一次隐藏层的值S。权重矩阵W就是隐藏层上一次的值（上一次的S）作为这一次的输入的权重。
在看来一下更加具体的图：

然后RNN循环神经网络的特点也在图中的一条中式子里表现了出来： $S_t = f(U·X_t + W·S_{t-1})$ ，进一步说明了隐藏层的值 $S_t$ 不仅仅取决于当前这次的输入 $X$ ，还取决于上一次隐藏层的值 $S_{t-1}$ 。我们从上图就能够很清楚的看到，上一时刻的隐藏层是如何影响当前时刻的隐藏层的。
最后我们再来看一个图（之前有一个图的展开形式）：

有了前面的例子，大家再来看这张图应该就清晰很多了吧，是不是有一种豁然开朗的感觉呢？

二、长短时记忆网络LSTM

其实我们刚才在前面提到，RNN循环神经网络它的创新之处就在于将序列的信息节点之间建立起了联系，上文会影响下文的输出。那如果我们换一个角度或者换一种说法的话，我们是不是可以理解为上一个节点的部分“记忆”被保留到了当前节点并对当前节点产生了一定的影响。
我觉得这样大家就大概对本节“长短时记忆网络”(Long Short-Term Memory)中所谓的“记忆”有了初步的认识。

1.背景

标准RNN可以处理不太长的相关信息间隔：
例如，预测语句"the clouds are in the ____“的空格中的词。

我们可以尝试去简单分析一下这个例子，显然按照常理的话，空格中我们希望预测出的词应该是"sky”，而RNN通过上文的“记忆”影响，能让空格中预测出的是"sky"的最大的影响显然应该是来自前文的单词"clouds"（毕竟语义上关系最相近，“云”&“天空”，这不是天仙配吗？），也就是上图中标红的输入 $x_1$ 会影响到标红的输出 $o_5$ 。
但标准RNN无法处理更长的上下文间隔，即长期依赖问题：
例如，预测"I grew up in France…(省略了很多词)I speak fluent ____"最后的词。

标准RNN在处理长期依赖问题时，梯度下降法训练RNN容易发生梯度消失/爆炸

2.RNN的梯度消失/爆炸

根据前面的例子我们可以知道，RNN的结构特点主要可以由这样一条式子归纳： $h_t = f(x_t,h_{t-1};\theta)$ 对参数 $\theta$ 求导 $\frac{d h_t}{d \theta} = \frac{\partial h_t}{\partial h_{t-1}} \frac{dh_{t-1}}{d \theta} + \frac{\partial h_t}{\partial \theta}$
同时，从上式我们就可以看出，其实梯度消失或者梯度爆炸现象几乎是必然存在的。
求梯度的步数多了，一层又一层，我们不可能奢望梯度每次都最终稳定在1附近，这样概率太小了小，需要很精巧地设计模型才行，所以梯度消失或爆炸几乎都是不可避免的，我们只能限制有限的步数去缓解这个问题，这也就是为什么传统的RNN只能解决不太长的相关信息间隔的问题。

3.LSTM结构

LSTM(Long Short-Term Memory)，即长短期记忆网络，是RNN的扩展，其通过特殊的结构设计来避免长期依赖问题。
如下图，LSTM的基本架构与RNN类似，它相当于是在RNN的基础上添加了一系列的“记忆单元”，用符号C来表示.。我们前面提到过再RNN中， $h_t$ 是由 $h_{t-1}$ 和 $x_t$ 决定的，而在LSTM模型中， $h_t$ 是由 $h_{t-1}$ 、 $x_t$ 和 $C_{t-1}$ 决定的。每一个时间节点的“记忆单元”C相连，形成上下文的语义影响，构成了一条贯穿全文的“记忆线”，这也正是LSTM模型能够处理更长的上下文间隔，即长期依赖问题的根本所在。
如下是神经网络中常见的一些门操作，有助于理解后续的LSTM结构
下面就一起来看一下LSTM的整体框架

可能乍一看到这张图大家会有一些懵，其实我们可以先把这个大圈内部的细节给忽略掉，它其实就相当于是一个黑盒子，我们给定 $C_{t-1},h_{t-1},x_t$ 进入黑盒子，然后经过黑盒子的内部得到 $C_t,h_t$ ，其中 $C_{t-1},h_{t-1}$ 是上一时间节点的“记忆单元”和输出， $x_t,C_t,h_t$ 分别是当前时间节点的输入、“记忆单元”和输出。
然后为了对LSTM模型有一个更加具体的认识，我们现在再一步一步的剖析LSTM黑盒子内的内部构造：

STEP1:
请添加图片描述

前面提到在LSTM模型中， $h_t$ 是由 $h_{t-1}$ 、 $x_t$ 和 $C_{t-1}$ 决定的，而“记忆单元” $C_{t-1}$ 也就是可以理解为上一个时间节点留给当前时间节点的记忆或者上个时间的部分信息会通过所谓“记忆”的形式影响到下一个时间节点的信息。如果大家仔细看的会发现我说的是部分信息，而不是所有信息，那么我们又要如何来实现这个“部分信息”的筛选呢？
这就要运用到我在前面提到过的“乘法门”来实现信息的选择性输出，其实“乘法门”的本质就是作一层 $s i g m o i d$ 得到取值范围为 $[0, 1]$ 的数，然后与之相乘。大家可以想象一下一个数 $x$ 和另一个取值范围为 $[0, 1]$ 的数 $y$ 相乘，那是不是可以理解为 $y$ 就是 $x$ 的保留程度或者说是忘记程度呢？得到的乘积 $x y$ 也就是 $x$ 在通过 $y$ 的筛选后的剩余结果。
在LSTM模型中，我们将上一时间节点的输出 $h_{t-1}$ 和当前时间节点的输入 $x_t$ 做了一定的处理后作一层 $s i g m o i d$ 得到 $f_t$ ， $f_t = \sigma(W_f·[h_{t-1},x_t] + b_f)$ ， $f_t$ 的取值范围为 $[0, 1]$ ，然后将 $f_t$ 与上一时间节点的“记忆单元” $C_{t-1}$ 相乘，也就相当于给上一时间节点的“记忆单元” $C_{t-1}$ 做了信息筛选，实现了部分信息的“选拔”！

STEP2:

STEP1中我们得到了上一个时间节点的“记忆信息”，那么我们现在来考虑一下如何计算出我们当前时间节点的“记忆信息”吧，以便传输给下一个时间节点。
首先，同样是对上一时间节点的输出 $h_{t-1}$ 和当前时间节点的输入 $x_t$ 做了一定的处理后作一层 $t a n h$ 的规范化（tanh函数的作用是是把目标值映射到[-1,1]的范围内去），得到当前节点的信息 $C_t'$ ，然后同样是对 $C_t'$ 的信息作一次筛选（原理同STEP1中提到的）。
然而在当前节点的信息 $C_t'$ 做完筛选之后，它仍然不能当作我们当前节点的“记忆信息” $C_t$ 去传输到下一个节点，因为正如上图中给出的， $C_t'$ 需要和上一时间节点的“记忆信息” $C_{t-1}$ 作一个“加法门”，也就是在 $C_{t-1}$ 的基础上更新 $C_t'$ 的信息。相信为什么要这么做大家应该是可以理解的，因为LSTM模型不同于RNN，我们要实现的是信息的长期依赖问题，所以传递给下一个节点的信息中显然不应该只包含当前节点的信息，还应该有上一节点、上上节点、上上上节点……
故，我们总结一下， $C_t = f_t \bigotimes C_{t-1} + i_t \bigotimes C_t'$

STEP3:

OK！前面讲的都是关于LSTM在“记忆”这一特异功能上的内容，接下来我们回归到更加实际的部分，也就是我们的输出到底是哪里来的。
嘿嘿！有了前面的经验再来看这张图是不是一下就看懂了呢？
其实当前节点的输出 $h_t$ 是由 $h_{t-1}$ 、 $x_t$ 和 $C_{t-1}$ 决定的。同样是对上一时间节点的输出 $h_{t-1}$ 和当前时间节点的输入 $x_t$ 做了一定的处理后作一层 $s i g m o i d$ ，然后和做了一层 $t a n h$ 的 $C_t$ 做一个“乘法门”，就得到了我们当前时间节点的输出啦！（这里的介绍比较简单，相信大家看过前面的内容再看到这里应该是很容易就看得懂的啦！）

三、LSTM的变体

接下来的内容我就不一一细说啦，其实都是在传统LSTM的基础上稍稍做了一点点改动。
看不懂的给我吊在电风扇上打屁股，然后给我回去好好的先把前面的看懂了再回来看这里！！！（手动狗头）

1.peephole connection

由 Gers & Schmidhuber (2000) 提出，增加了 “peephole connection”。门层也接受长期状态的输入。
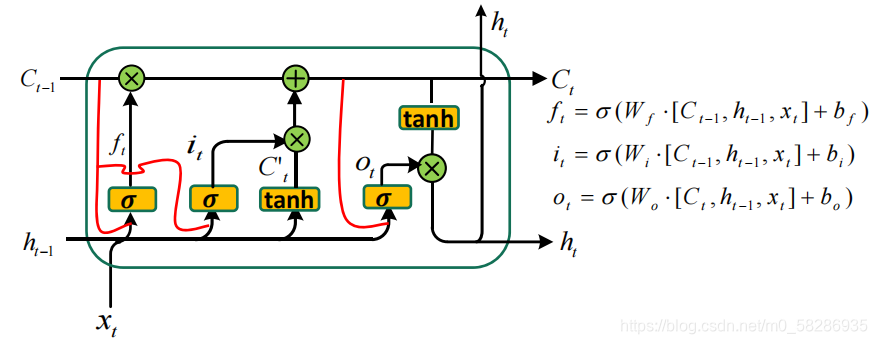
你看我就说内容变化不大吧。其实就是在 $s i g m o i d$ 层的时候，在 $s i g m o i d$ 层的输入信息里把当前时间节点的“记忆信息” $C_t$ 也给带上就OK啦！

2.耦合(coupled)遗忘和输入单元

耦合(coupled)遗忘和输入单元：将遗忘和新记忆两个过程耦合，即只遗忘那些有新元素来填充的元素。
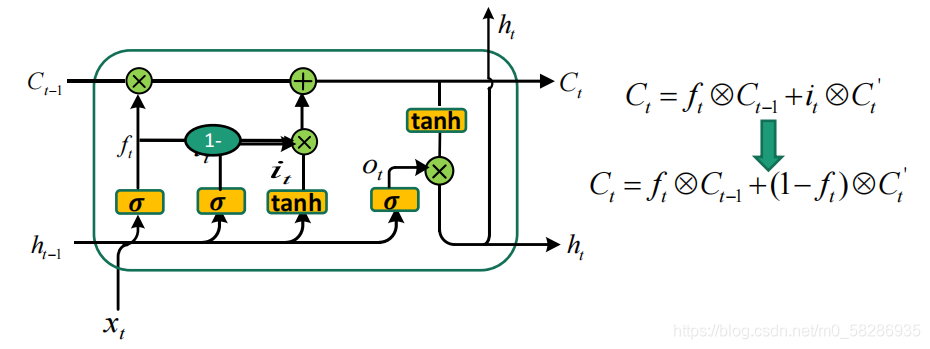
本来的LSTM的当前时间节点“记忆信息” $C_t = f_t \bigotimes C_{t-1} + i_t \bigotimes C_t'$ ，这里的 $f_t$ 和 $i_t$ 其实都是 $s i g m o i d$ 层的输出结果，就是拿来做信息筛选的。只不过在这一种LSTM变体中，我们做一个耦合，我们把 $C_{t-1}$ 和 $C_t'$ 的信息筛选都交给 $f_t$ 来做，只不过一个是 $f_t$ ，另一个是 $1-f_t$ 罢了。最终得到 $C_t = f_t \bigotimes C_{t-1} + (1-f_t) \bigotimes C_t'$

3.GRU

即Gated Recurrent Unit Cho, et al. (2014)，混合了长期状态和隐藏状态。
乍一看GRU的时候我也被吓到了，LSTM的经典标志“记忆单元”C怎么给整不见了呢
但是咱们再仔细看看标题的含义——混合了长期状态和隐藏状态。这里的长期状态其实就是之我们的“记忆单元”C，隐藏状态就是指我们的隐藏层节点输出h，所以C只是被混合到了h中，可别不认识它了喔。
我们再试着简单分析一下， $h_{t-1}$ 既是上一时间节点的输出也是上一节点的“记忆单元”， $x_t$ 仍然代表当前时间节点的输入， $\widetilde{h}_t$ 代表的就是当前节点的内容信息。 $h_t = z_t \bigotimes \widetilde{h}_t + (1-z_t) \bigotimes h_{t-1}$ 就是说把当前节点的内容信息 $\widetilde{h}_t$ 和上一时间节点的“记忆信息” $h_{t-1}$ 分别做一个 $s i g m o i d$ 后相加，得到的值不仅仅是当前节点的“记忆信息”，也还是当前节点的“输出信息”。