节点嵌入
图表示学习
图表示学习(Graph Representation Learning)使得图机器学习摆脱了传统图机器学习对特征工程的依赖。
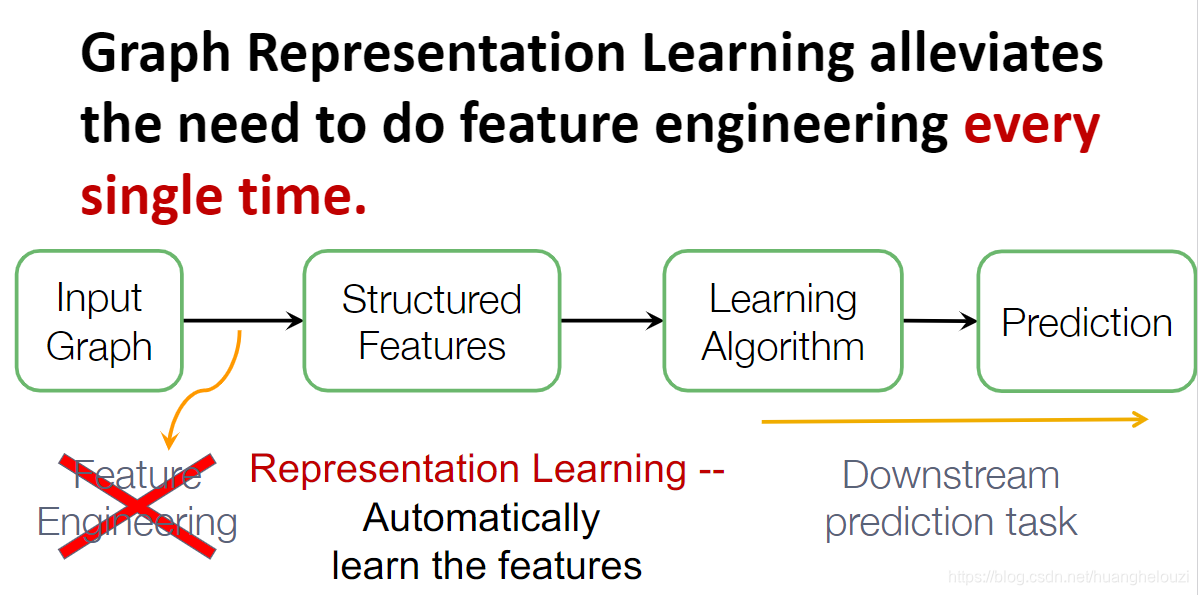
图表示学习的目标是为图机器学习高效地学习出独立于特定下游任务的特征表示(节点嵌入),这个过程很像降维。
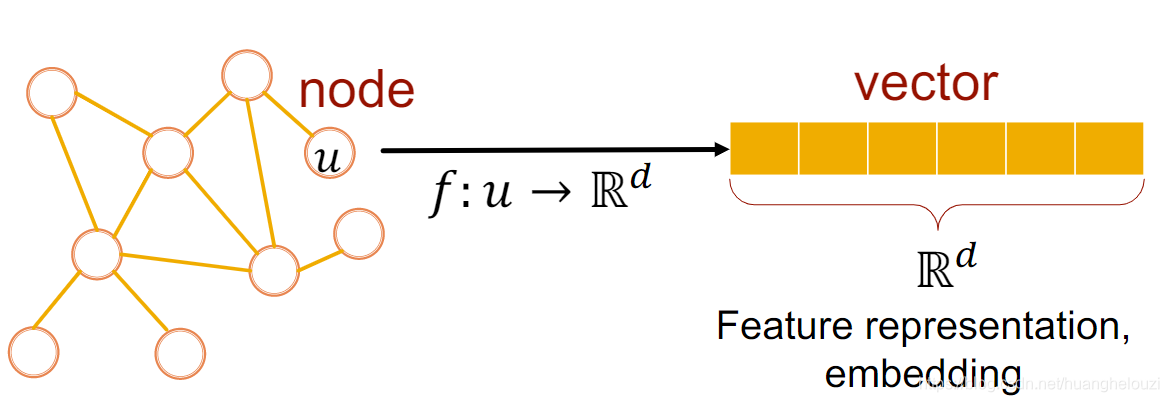
图表示学习的任务是将节点映射到嵌入空间,当然不可随意的映射,主要有以下的要求:
- 在图中相似的节点在特征空间(嵌入空间)中的嵌入仍然相似,何为相似的节点?比如存在边相连的两个节点;
- 节点嵌入应包含图结构信息、节点本身信息;
- 这些嵌入可能被使用在很多的下游任务,这要求嵌入与任务无关。

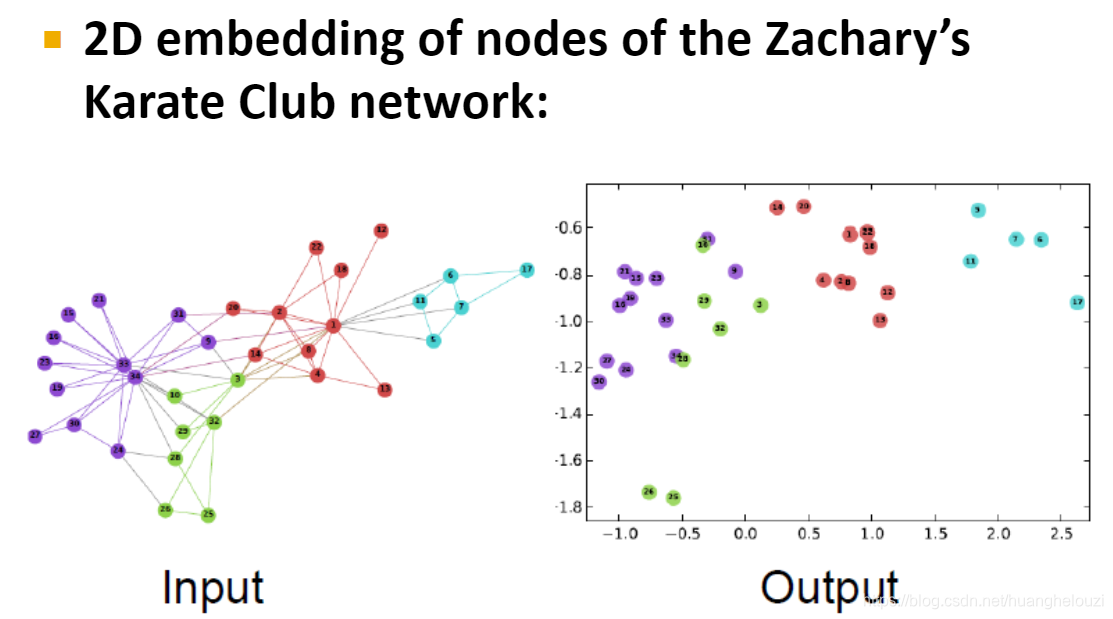
下面给出achary’s Karate Club网络的节点嵌入的例子,右边子图可视化了该网络的节点嵌入,我们可以发现属于同一类别(以不同颜色区分不同类别)节点的嵌入彼此都比较接近,即在图中相似的节点在特征空间(嵌入空间)中的嵌入仍然相似。
下面介绍几种常见的获取节点嵌入的方法,分别是Encoder and Decoder等。
Encoder and Decoder方案
我们假定有图
G
(
V
,
E
)
G(V,E)
G(V,E),其中
V
V
V为节点集(顶点集),
E
E
E为边集。为了简单起见,我们忽略节点特征和其他额外的信息。
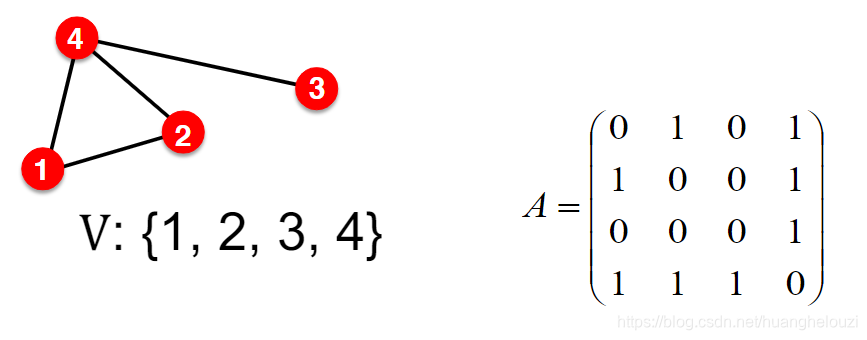
该目标是对节点进行编码(Encode),使得在嵌入空间中的节点特征相似性近似于在图中的节点相似性,相似性可用点积(dot product)衡量,其他常见的还有余弦相似度、欧式距离、马氏距离等等。
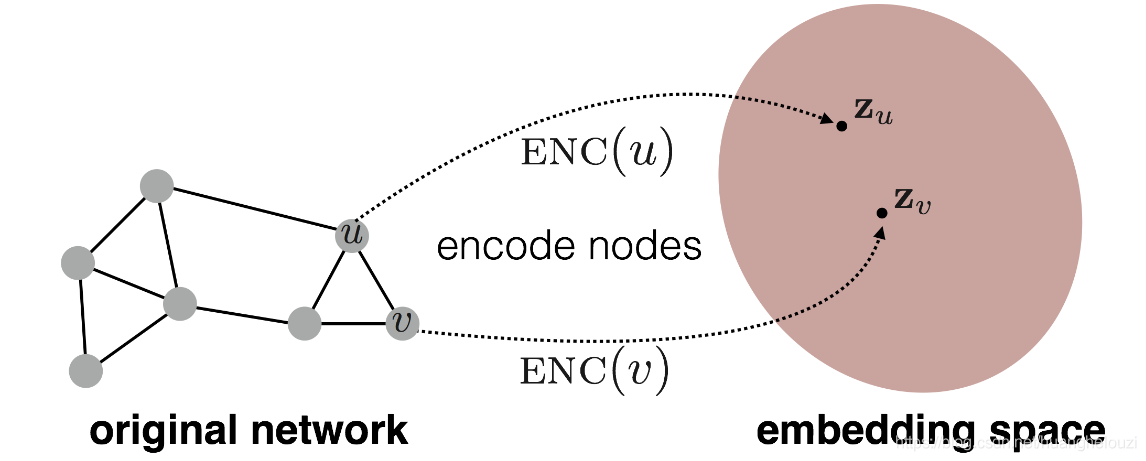
嵌入空间中的节点特征相似性需要近似在图中的节点相似性:
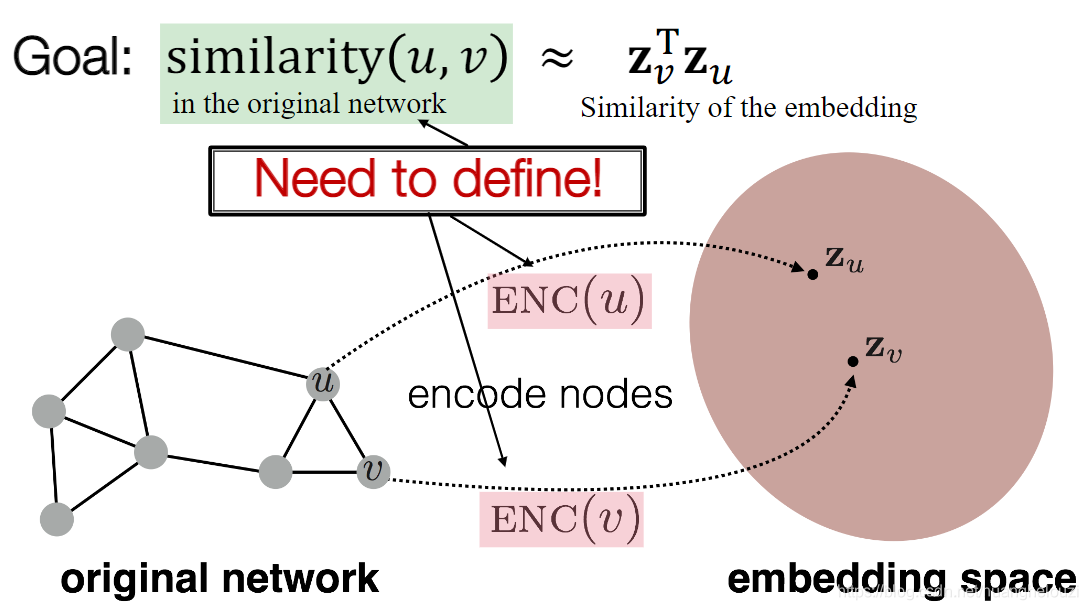
Encoder and Decoder方案可描述为:

其中Encoder和相似性函数作用为:

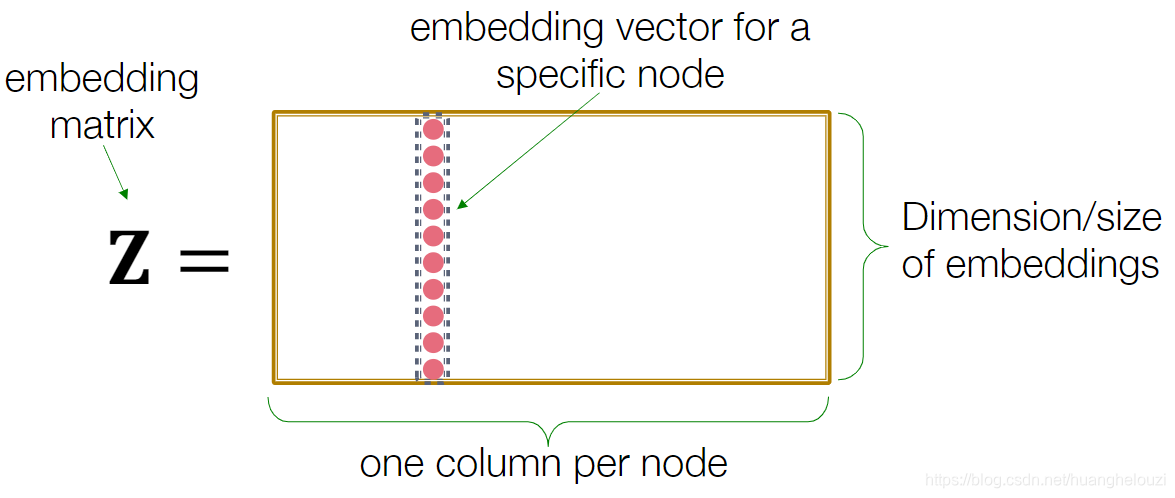
Encoder and Decoder方案一种最简单的实现为:embedding-lookup

从上面我们可以发现,该方案的核心是选择一个合适的节点相似性。而两个节点拥有相似的节点嵌入它们应该具有以下特征:
- 比较“相像”
- 拥有共享邻居节点
- 在图结构中扮演相似的角色
随机游走(Rondom Walk)
下面将介绍使用随机游动定义节点相似性,以及如何为这种相似性度量优化嵌入。
首先给出下文需要的一些定义:

随机游走的定义和例子在这给出:
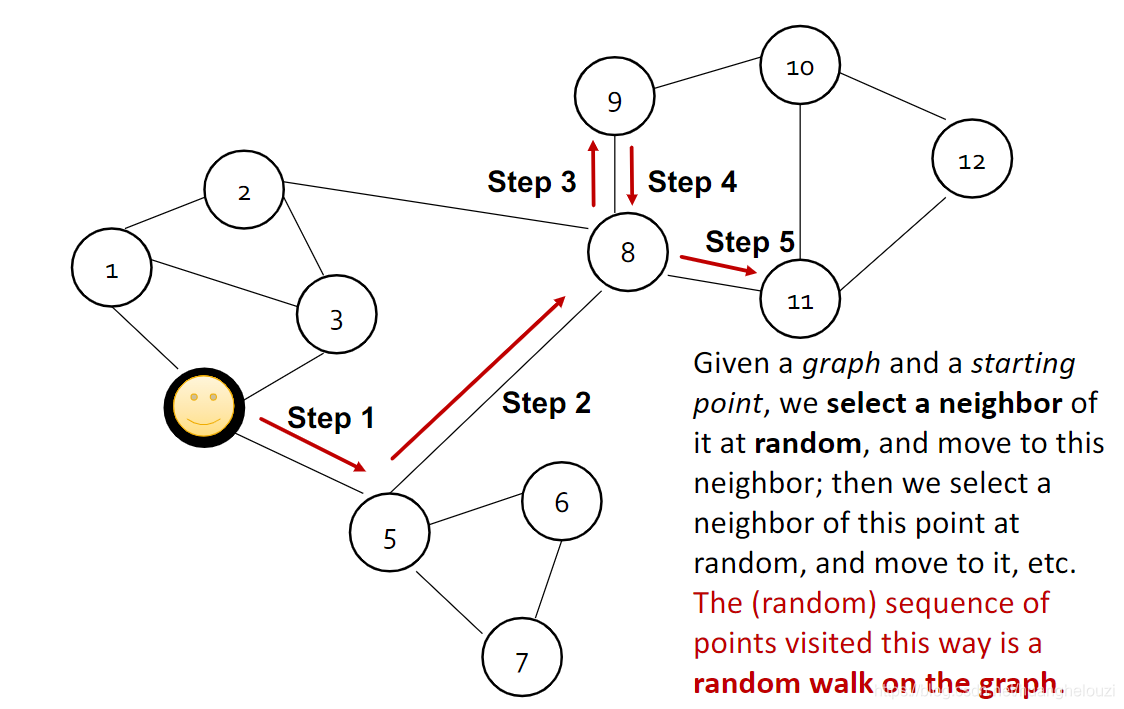
在随机游走中,两个节点嵌入的相似性等于这两个节点共同出现在某个随机游走序列中的概率。

随机游走优化问题可定义为:
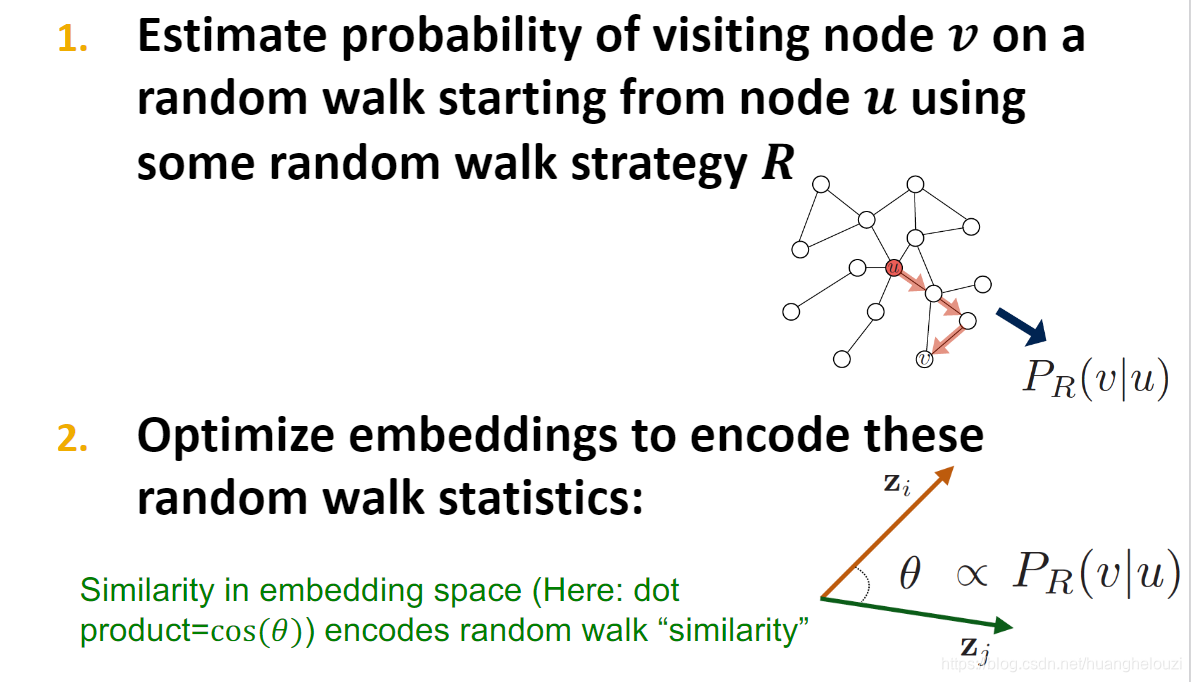
选择随机游走的原因主要有两个:(1)Expressivity;(2)Efficiency。

该优化问题和相关描述变成:




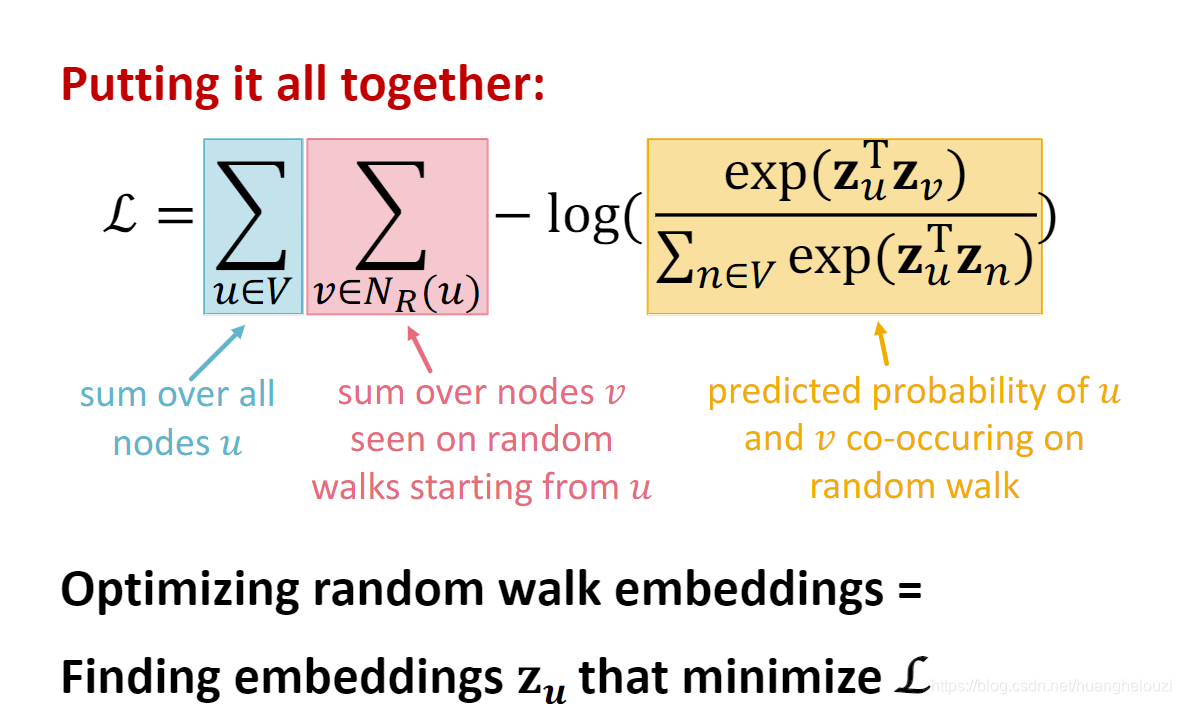
由于该方法计算复杂性太高,故采用下采样方法进行近似:



deepwalk更多内容可以参考知乎

其他的节点嵌入方法还有node2vec。
node2vec
可看知乎
整图嵌入
整图嵌入是为了整个图获取嵌入表达,而节点嵌入是为了获取各个节点的嵌入(废话)。
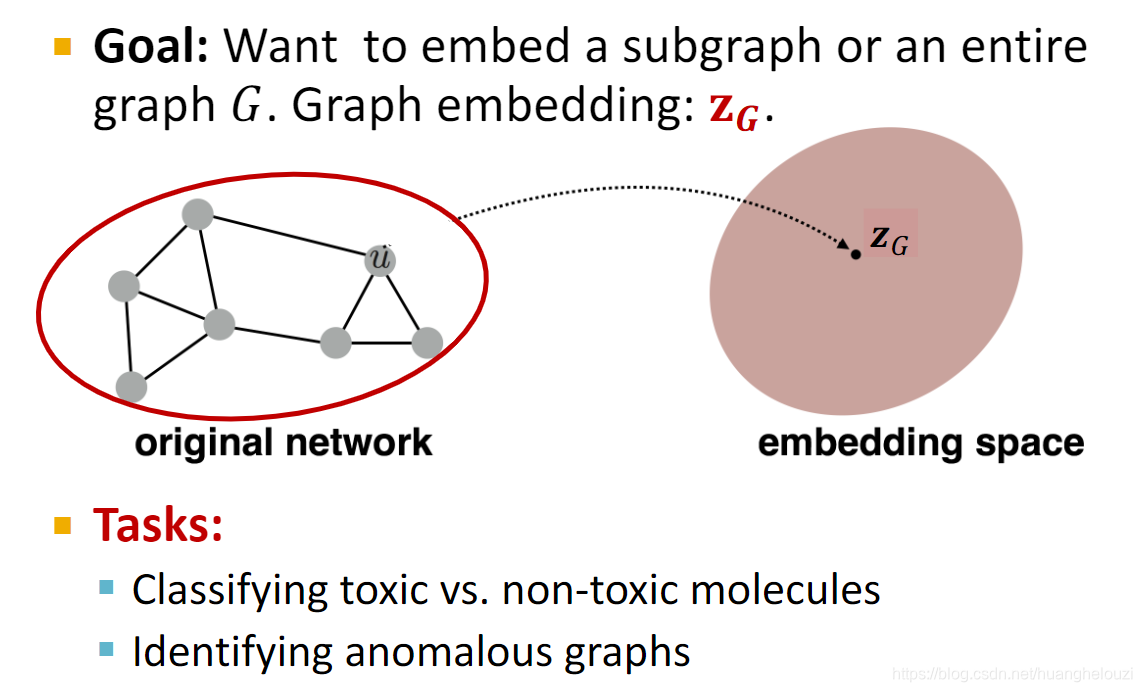
一种简单的整图嵌入方法如下
- 使用现有的节点嵌入方法获取每个节点的嵌入;
- 对节点嵌入简单的应用
加法或者mean获取整图嵌入;

Duvenaud et al., 2016
另外一种简单实现如下:通过引入虚拟节点获取整图嵌入:
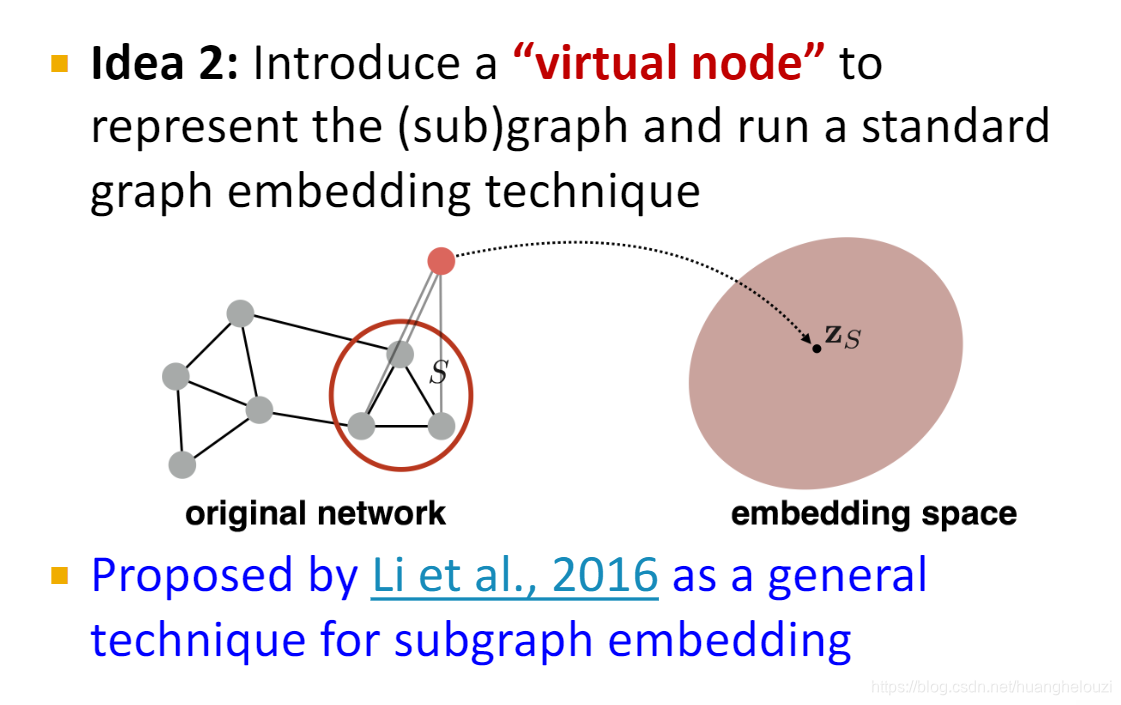
Li et al., 2016