诸神缄默不语-个人CSDN博文目录
cs224w(图机器学习)2021冬季课程学习笔记集合
文章目录
本节课slides 下载地址
同上一篇博文:
YouTube 视频观看地址1 视频观看地址2 视频观看地址3
本章主要内容:
本章首先介绍了图中motif / subgraph的概念,以及对motif significance的定义(即定义图中的subgraph要比null model多/少出多少才算显著,以及如何生成null model)。
接下来介绍了神经网络模型下的subgraph matching方法(同时也是subgraph的表示方法)。
最后介绍如何找到图中出现频率较高的motif / subgraph。
1. Identifying and Counting Motifs in Networks
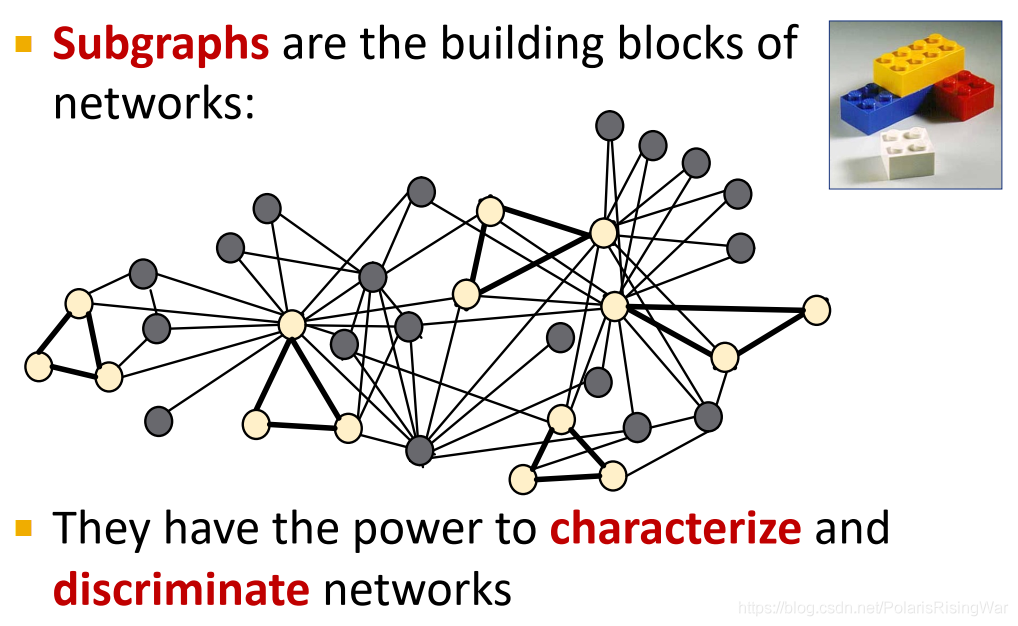
- subgraph
subgraph是网络的组成部分,可用于识别和区分不同的网络(可以说是不同种类网络会具有不同特征的subgraph)。
使用传统的discrete type matching1 方法代价很大,本文会介绍使用神经网络解决subgraph matching问题的方法。
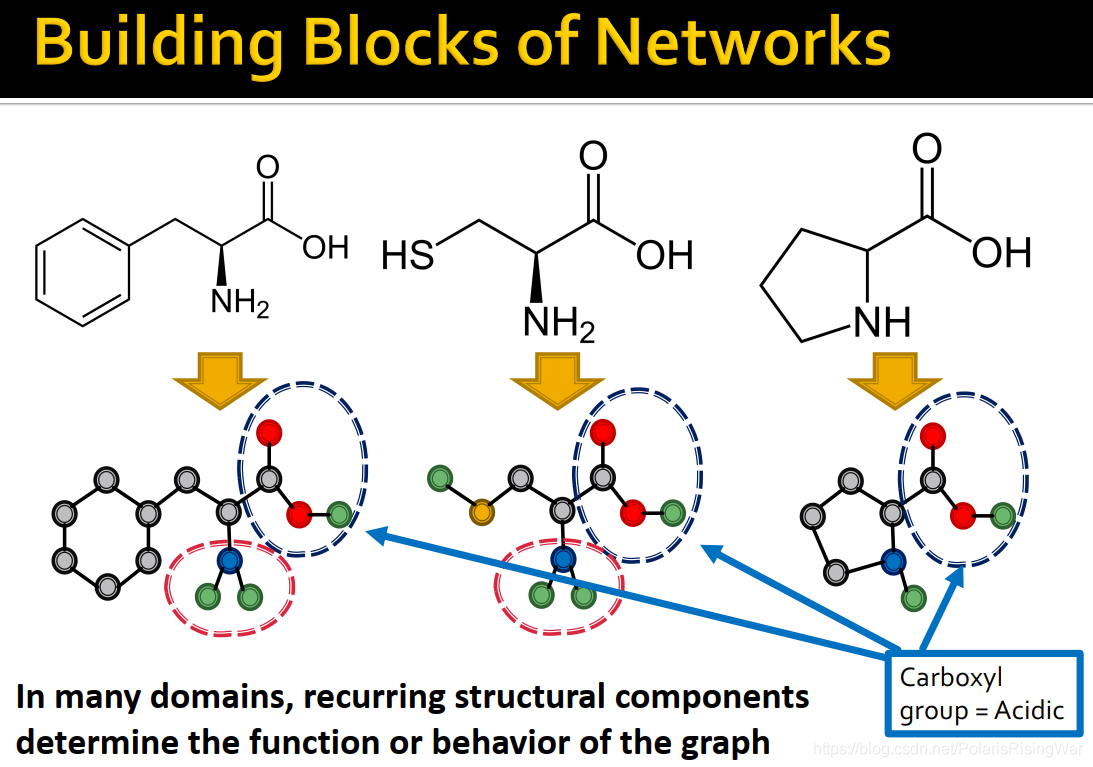
- 以下图分子式为例:含有羧基(subgraph)的分子(graph)是羧酸(group)
2. Subgraph and Motifs
2.1 Defining Subgraphs and Motifs
- subgraph定义
对于图 G = ( V , E ) \mathbf{G}=(\mathbf{V},\mathbf{E}) G=(V,E) 有两种定义其subgraph的方式:- node-induced subgraph / induced subgraph:常用定义
图中的一个节点子集+原图中两个节点都在该节点子集内的边(即edges induced by the nodes)
G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′) 是 node induced subgraph,当且仅当:
V ′ ? V V'\subseteq V V′?V
E ′ = { ( u , v ) ∈ E ? ∣ ? u , v ∈ V ′ } E'=\{(u,v)\in E\ |\ u,v\in V'\} E′={(u,v)∈E?∣?u,v∈V′} 时
G ′ G' G′ is the subgraph of G induced by V ′ V' V′

- edge-induced subgraph / non-induced subgraph / subgraph
图中的一个边子集+该子集的对应节点
G ′ = ( V ′ , E ′ ) G'=(V',E') G′=(V′,E′) 是 edge induced subgraph,当且仅当:
E ′ ? E E'\subseteq E E′?E
V ′ = { v ∈ V ? ∣ ? ( v , u ) ∈ E ′ ?for?some? u } V'=\{v\in V\ |\ (v,u)\in E'\ \text{for some}\ u\} V′={v∈V?∣?(v,u)∈E′?for?some?u} 时(我没看懂,意思应该是包含这些边的全部节点。就是说选了边之后节点自然就确定了,所以是non-induced。参考2)

- 具体使用哪种定义取决于问题领域。
如在化学领域中常使用node-induced概念(官能团),在知识图谱中常用edge-induced概念(我们关心的是代表逻辑关系的边)。

- node-induced subgraph / induced subgraph:常用定义
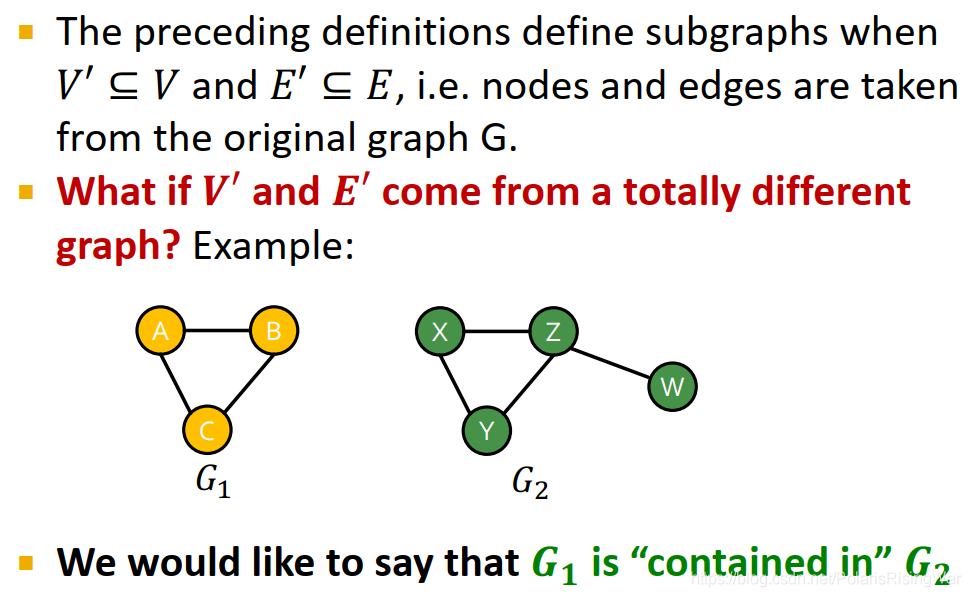
- 前文对subgraph的定义都需要
V
′
?
V
V'\subseteq V
V′?V 且
E
′
?
E
E'\subseteq E
E′?E,即
V
′
V'
V′ 和
E
′
E'
E′ 都出自原图。如果节点和边出自不同的图但仍有对应关系,如下图所示,我们称这种情况为
G
1
\mathbf{G}_1
G1? is contained in
G
2
\mathbf{G}_2
G2?
- graph isomorphism图同构
如果 G 1 G_1 G1? 和 G 2 G_2 G2? 存在双射关系 f : V 1 → V 2 f:V_1\rightarrow V_2 f:V1?→V2?,使得当且仅当 ( f ( u ) , f ( v ) ) ∈ E 2 \big(f(u),f(v)\big)\in E_2 (f(u),f(v))∈E2? 时, ( u , v ) ∈ E 1 (u,v)\in E_1 (u,v)∈E1?(即 G 1 G_1 G1? 中的节点能一一映射到 G 2 G_2 G2? 中的节点,使节点之间对应的边关系也能同时映射到另一个图所对应的节点之间)。我们称两个图同构。
图中ab是uv写错了。
如下图左图所示(节点颜色表示映射关系)。
因为节点没有固定顺序,所以我们不知道节点之间是怎么映射的,所以我们需要遍历所有可能。
检验图是否同构的问题是否NP-hard未知,但至今没有提出polynomial algorithm。

- subgraph isomorphism子图同构
如果 G 2 G_2 G2? 的子图与 G 1 G_1 G1? 同构,我们称 G 2 G_2 G2? is subgraph-isomorphic to G 1 G_1 G1?。
我们可以使用node-induced或edge-induced subgraph定义。
这一问题是NP-hrad的。
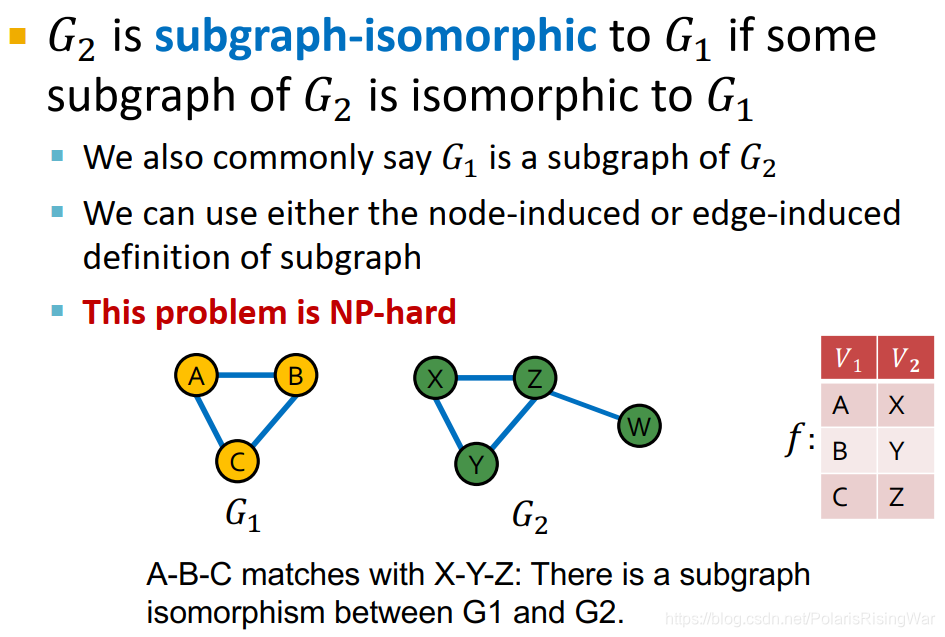
节点之间的映射不必唯一。 - subgraph举例
- 所有非同构的、connected、无向的4个节点的图:

- 所有非同构的、connected、有向的3个节点的图:
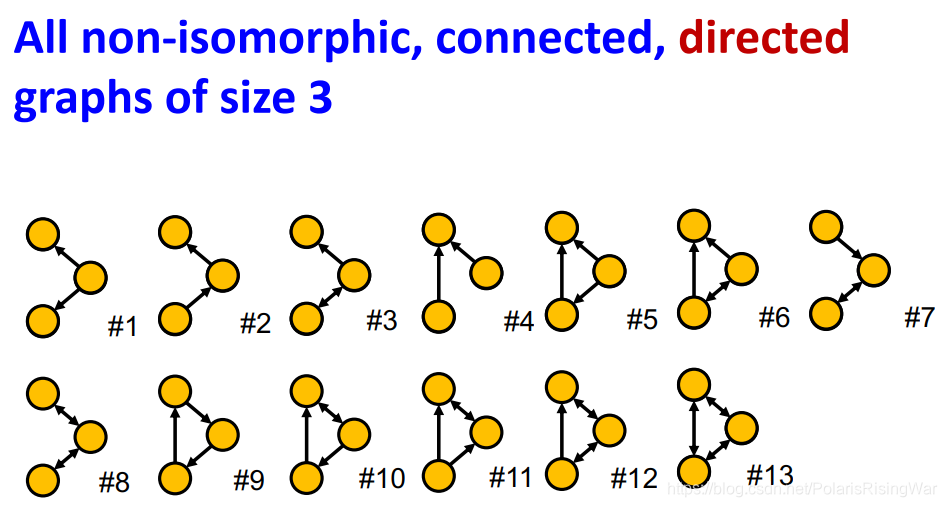
一般最多也就4-5个节点了
- 所有非同构的、connected、无向的4个节点的图:
- network motifs
定义:recurring, significant patterns of interconnections- pattern:小的node-induced subgraph
- recurring:出现很多次,即出现频率高(以下将介绍如何定义频率)
- signifant:比预期(如在随机生成的图中)出现的频率高(以下将介绍如何定义随机图)

- motif举例:
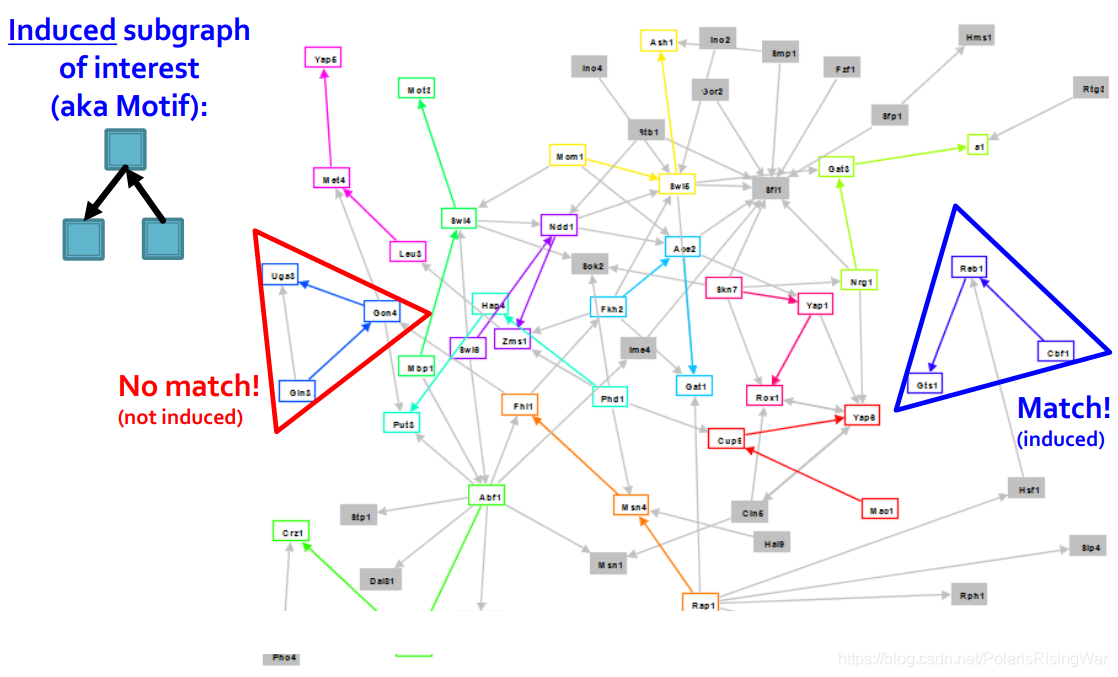 如图所示:左上角就是我们所感兴趣的induced subgraph(motif)。蓝三角内的induced subgraph符合要求,红三角内不是induced subgraph不符合要求。
如图所示:左上角就是我们所感兴趣的induced subgraph(motif)。蓝三角内的induced subgraph符合要求,红三角内不是induced subgraph不符合要求。 - motif的意义:
?1. 帮助我们了解图的工作机制。
?2. 帮助我们基于图数据集中某种subgraph的出现和没有出现来做出预测3。
举例:- feed-forward loops:神经元网络中用于中和biological noise

- parallel loops:食物链中(就两种生物以同一种生物为食并是同一种生物的猎物嘛)

- single-input modules:基因控制网络4 中


- feed-forward loops:神经元网络中用于中和biological noise
- subgraph frequency
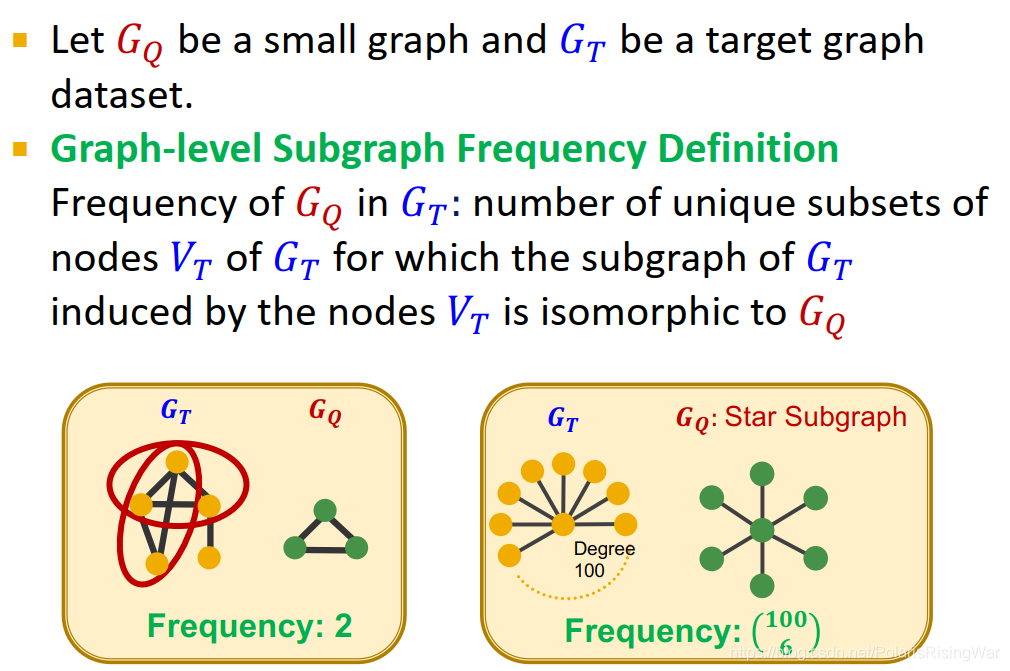
- 图级别的subgraph frequency定义
设 G Q G_Q GQ? 是一个小图, G T G_T GT? 是目标图数据集。
G Q G_Q GQ? 在 G T G_T GT? 中的频率: G T G_T GT? 不同的节点子集 V T V_T VT? 的数目( V T V_T VT? induce的 G T G_T GT? 的subgraph与 G Q G_Q GQ? 同构)
如下左图中frequency为2(红圈中的两种节点子集),右图中的frequency为 C 100 6 C_{100}^6 C1006?(图中的排列组合写法可以参考5)
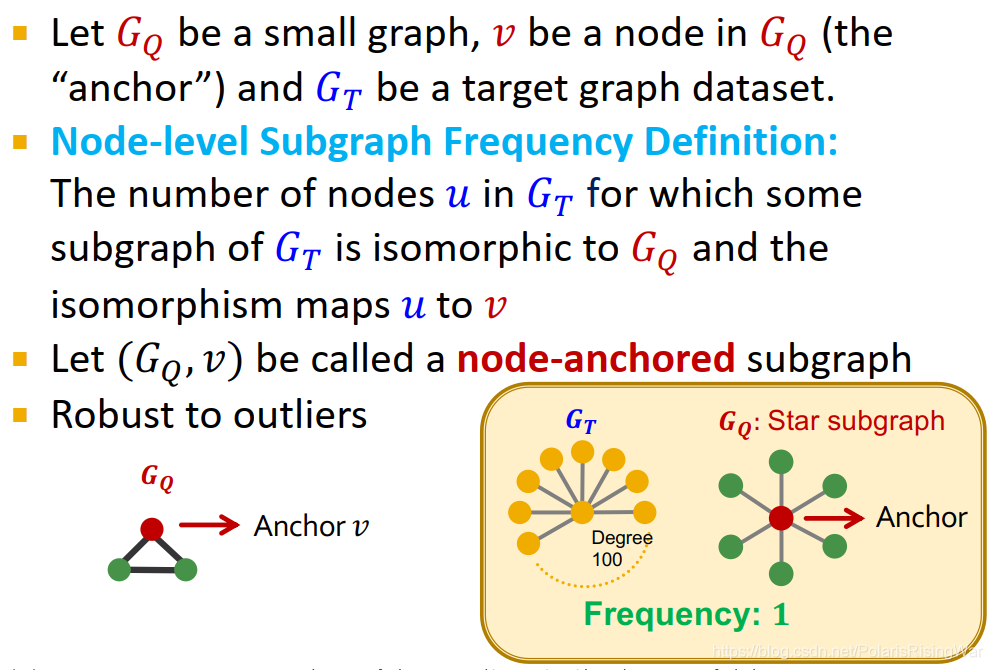
- 节点级别的subgraph frequency定义
设 G Q G_Q GQ? 是一个小图, v v v 是其一个节点(anchor), G T G_T GT? 是目标图数据集。
G Q G_Q GQ? 在 G T G_T GT? 中的频率: G T G_T GT? 中节点 u u u 的数目( G T G_T GT? 的subgraph与 G Q G_Q GQ? 同构,其同构映射 u u u 到 v v v 上)
( G Q , v ) (G_Q,v) (GQ?,v) 叫node-anchored subgraph
这种定义对异常值比较鲁棒。如在图例中,star subgraph以中心节点为anchor,其在 G T G_T GT? 中的frequency就是1;若以其外围节点作为anchor,则其frequency就是100
- 如果数据集中包含多个图,我们可将其视为一整个大图
G
T
G_T
GT?(包含disconnected components,各组成部分对应单个图)
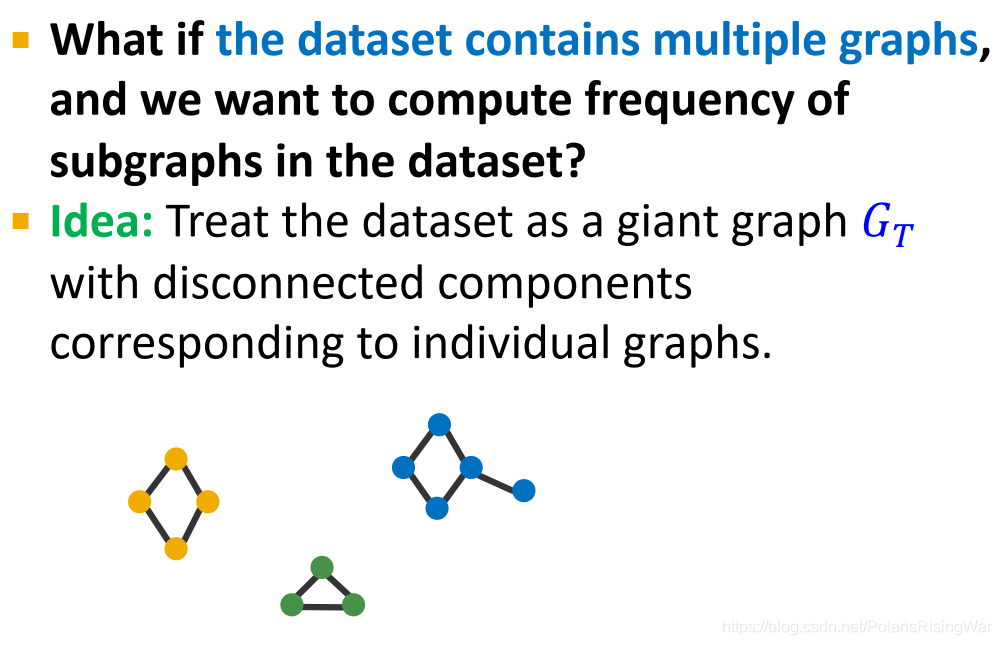
- 图级别的subgraph frequency定义
2.2 Determining Motif Significance
- 我们首先需要定义null-model
核心思想:在真实网络中比在随机网络中出现更频繁的subgraph有functional significance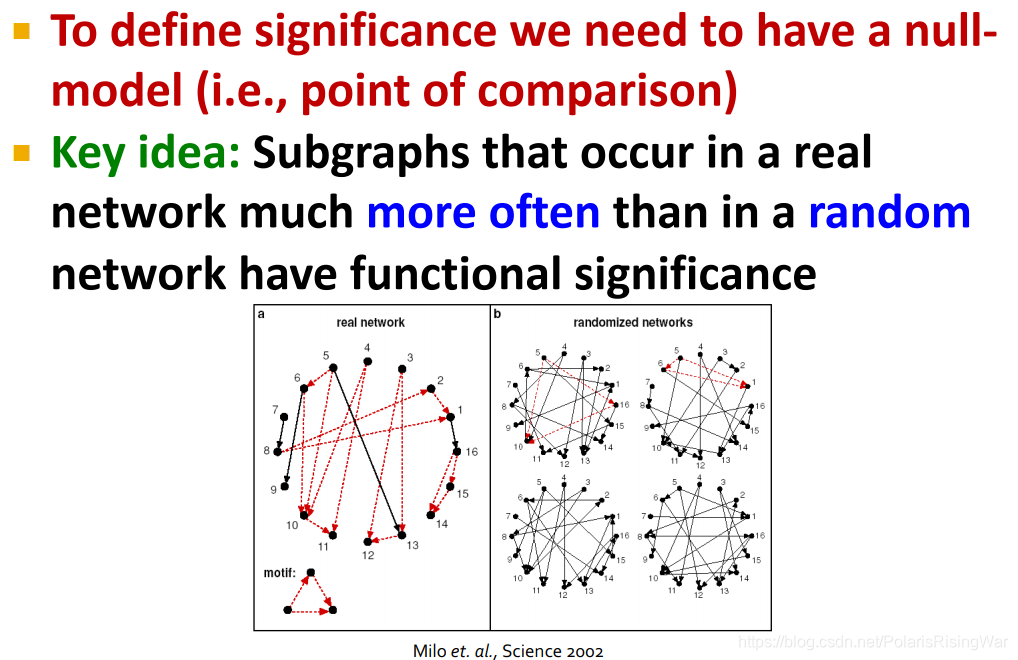
图中论文(配图出处):Zweig K A . Milo et al. (2002): Network Motifs: Simple Building Blocks of Complex Networks[M]. 2019. - 定义随机图:Erd?s–Rényi (ER) random graphs
G n , p G_{n,p} Gn,p?: n n n 个节点的无向图,每个边 ( u , v ) (u,v) (u,v) 以频率 p p p 独立同分布出现。
可以是disconnected:
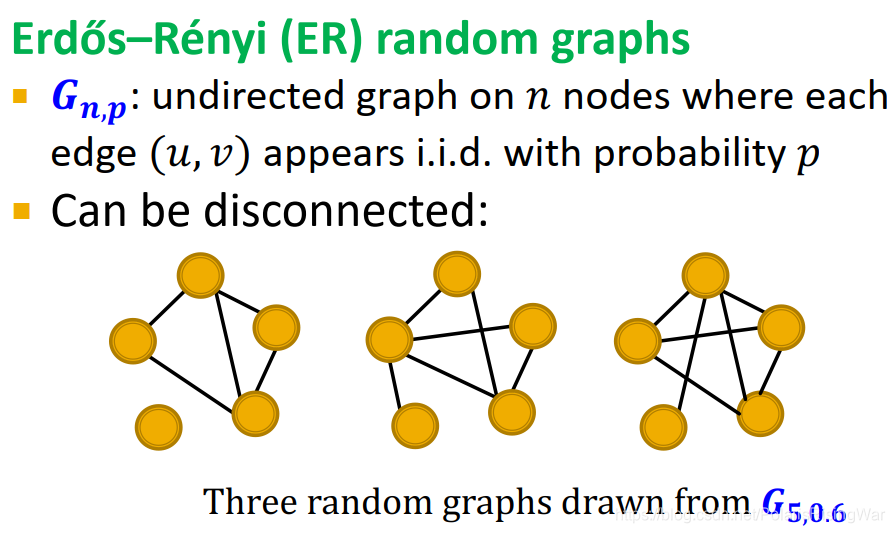
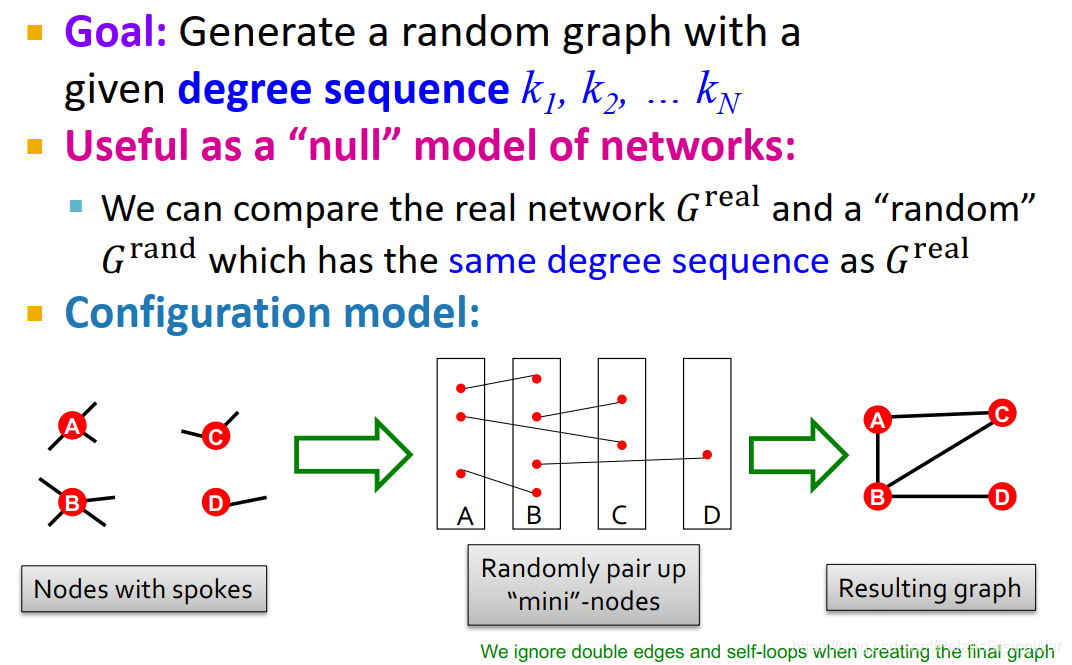
- 新模型:configuration model
目标:按照给定度数序列 k 1 , k 2 , . . . ? k N k_1,k_2,...\ k_N k1?,k2?,...?kN? 生成随机图。
作为网络的null model很有用,可以将真实图和与其具有相同度数序列的随机图作比。
configuration model流程如图所示:对节点上的边进行两两配对,得到最终的结果图(如果出现重边(multiple edges)6或自环的情况,由于其罕见,所以可以直接忽略。如图中A-B节点之间出现了double edge,但在最后的结果图中就忽略了,仅作为一条边来处理)
- 除了像上图那种节点辐条的做法,还可以使用switching方法:
对给定图 G G G,重复switching步骤 Q ? ∣ E ∣ Q\cdot|E| Q?∣E∣ 次:
?1. 随机选取一对边A→B,C→D
?2. 交换端点7 使A→D,C→B(仅在无重边或自环被产生时进行交换操作)
得到randomly rewired graph(与原图的节点度数相同)
Q Q Q 需足够大(如100)以使这个过程收敛8

- motif significance overview
检验motif在真实网络中是否比在随机图中overrepresent的步骤:- step1:在真实图中数motif的个数
- step2:产生多个与真实图有相同统计量(如节点数、边数、度数序列等)的随机图,在这些随机图中数motif的个数
- step3:使用统计指标衡量每一motif是否显著
用Z-score
- Z-score for statistical significance
Z i Z_i Zi? 捕获motif i i i 的statistical significance:
Z i = ( N i r e a l ? N  ̄ i r a n d ) / std ( N i r a n d ) Z_i=(N_i^{real}-\overline{N}_i^{rand})/\text{std}(N_i^{rand}) Zi?=(Nireal??Nirand?)/std(Nirand?)
其中 N i r e a l N_i^{real} Nireal? 是真实图中motif i i i 的个数, N  ̄ i r a n d \overline{N}_i^{rand} Nirand? 是随机图实例中motif i i i 的平均个数。
0就是说真实图和随机图中motif出现的一样多。绝对值大于29 时就算显著地多或者显著地少。
network significance profile (SP):
S P i = Z i / ∑ j Z j 2 SP_i=Z_i/\sqrt{\sum_jZ_j^2} SPi?=Zi?/j∑?Zj2??
S P SP SP 是归一化的Z-score向量,其维度取决于我们考虑的motif的数量。
S P SP SP 强调subgraph的相对重要性:在比较不同大小的网络时很重要,因为一般来说,大图会出现更高的Z-score9。

- significance profile
对每个subgraph,Z-score指标可用于分类subgraph significance:负数意味着under-representation,整数意味着over-representation。
network significance profile是具有所有subgraph大小上的值的feature vector。
接下来就可以比较随机图和不同图上的profile了。
不同网络举例: - significance profile示例:
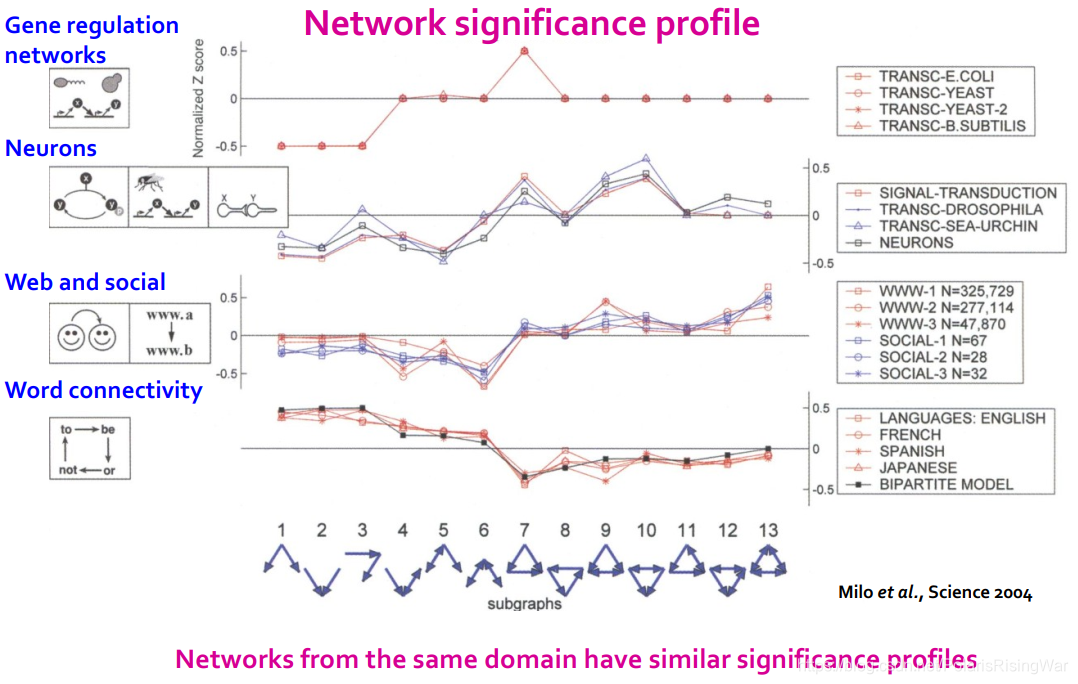 相似领域的网络会具有相似的SP。可以通过motif frequency来判断网络功能。如社交网络中的subgraph6少、但是subgraph13多,因为一个人很难同时与两人保持紧密好友关系而这两个人不互相认识,每周还要出来喝2次咖啡。毕竟如果他们认识以后就可以一周出来只约1次咖啡了。
相似领域的网络会具有相似的SP。可以通过motif frequency来判断网络功能。如社交网络中的subgraph6少、但是subgraph13多,因为一个人很难同时与两人保持紧密好友关系而这两个人不互相认识,每周还要出来喝2次咖啡。毕竟如果他们认识以后就可以一周出来只约1次咖啡了。 - 检测motif总结:

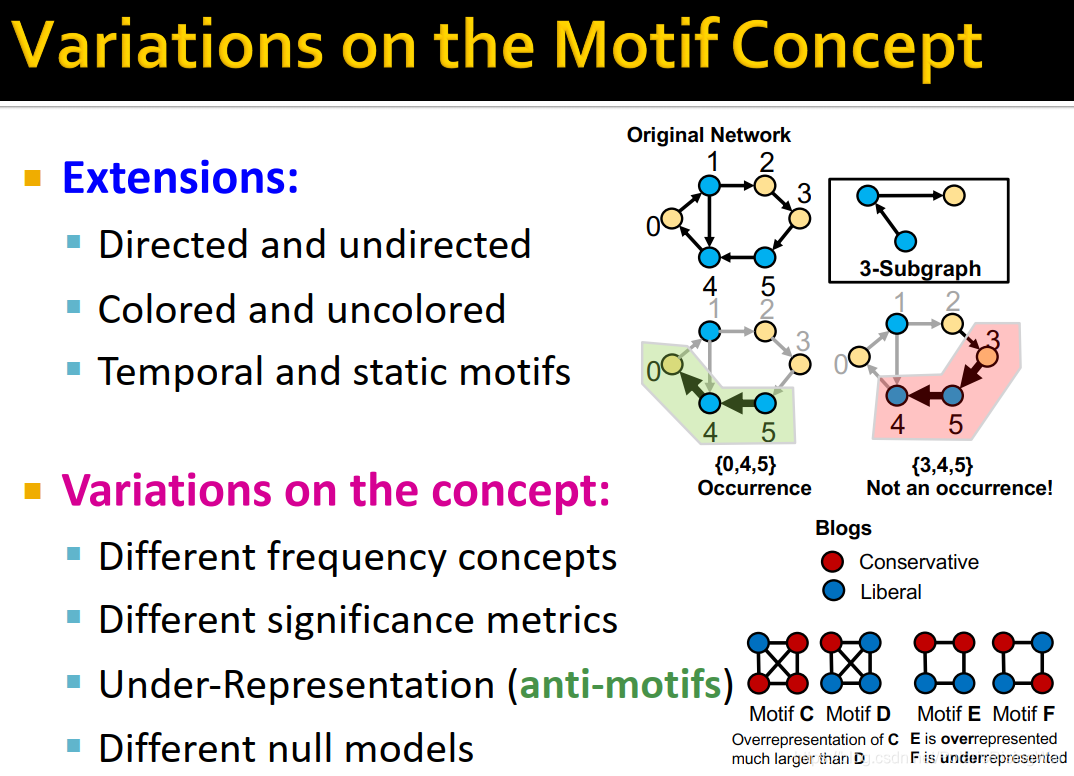
- motif概念的变体:
衍生:有向/无向,colored/uncolored(应该指的是节点类型,如下图中右上角045算motif出现、345不算motif出现的情况),动态/static motif
概念上的变体:不同的frequency概念、不同的significance指标、under-representation (anti-motifs)(如下图中右下角所示)、不同的null models
- motif总结:
subgraph和motif是图的组成部分,子图同构和技术问题是NP-hrad。
理解数据集中motif的频繁或显著出现,可以使我们了解该领域的独有特征。
使用随机图作为null model来通过Z-score衡量motif的显著性。

3. Neural Subgraph Matching / Representations
-
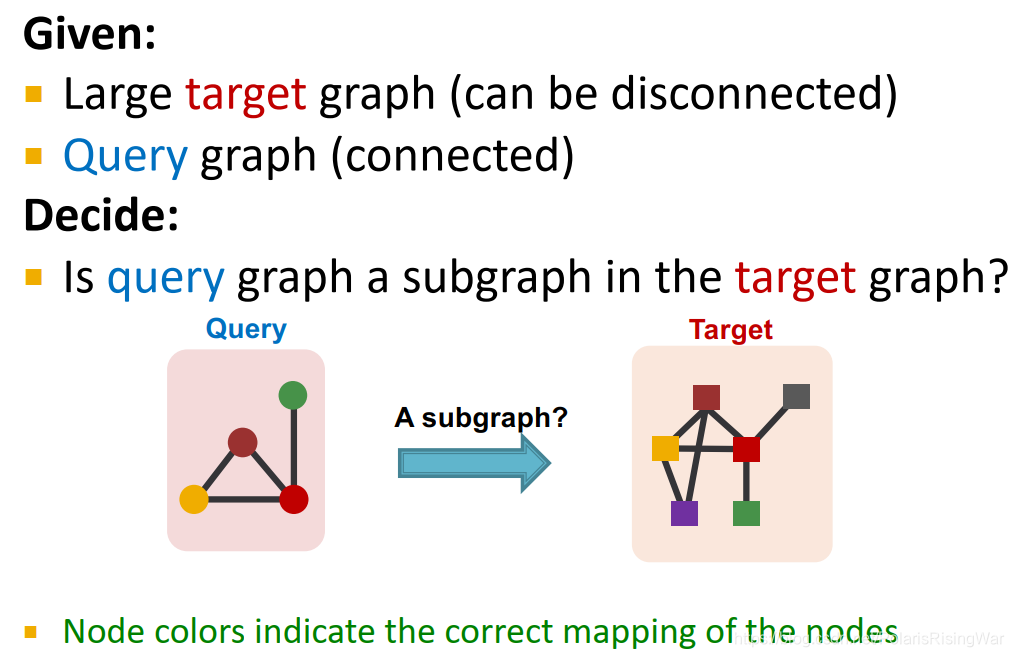
subgraph matching11
给出大的target graph(可以是disconnected),query graph(connected)
问题:query graph是否是target graph中的子图?
示例如下图(节点颜色表示映射关系):
-
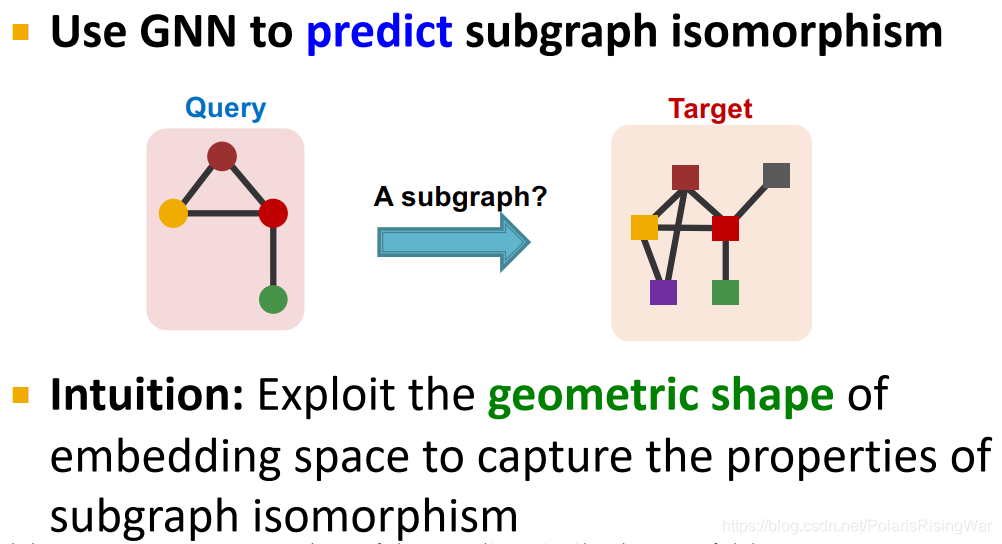
在本课程中我们不用combinatorial matching、逐边检查,而将该问题视作预测任务,使用机器学习方法来解决这一问题。
直觉:利用嵌入域的几何形状来捕获子图同构的属性12
-
task setup
二元预测问题:返回query是否与target graph子图同构
(注意在这里我们只关注该预测问题的最终决策,即是不是。而具体的节点之间如何一一对应的关系本课程中不讲)
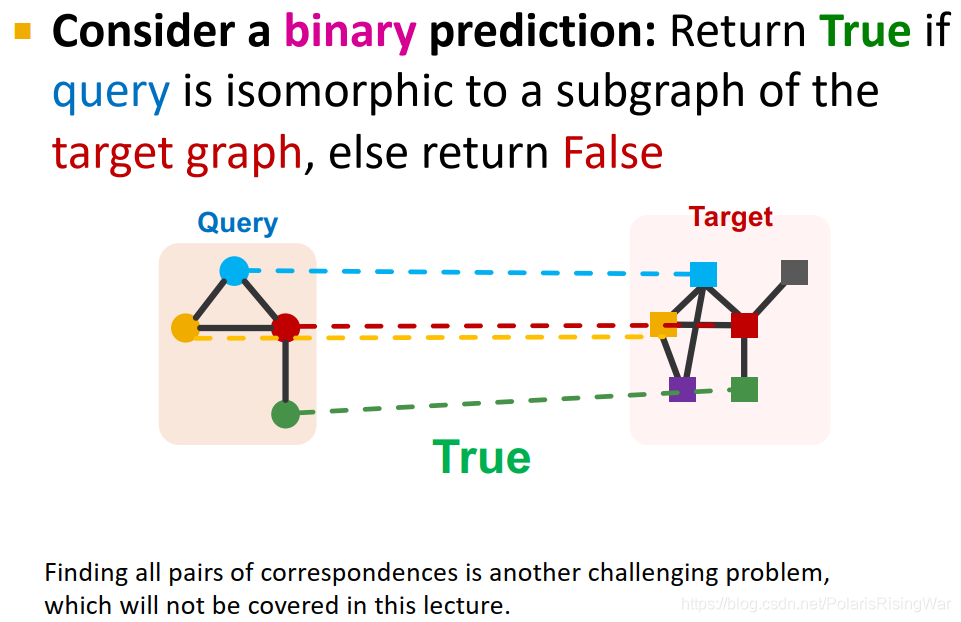
-
overview of the approach
整体流程如图所示:将target graph拆成很多neighborhoods,嵌入neighborhoods和query,将每个neighborhood与query做匹配,判断其是否子图同构:

-
neural architecture for subgraphs
- 我们将使用node-anchored定义,用anchor的嵌入来判断是否同构
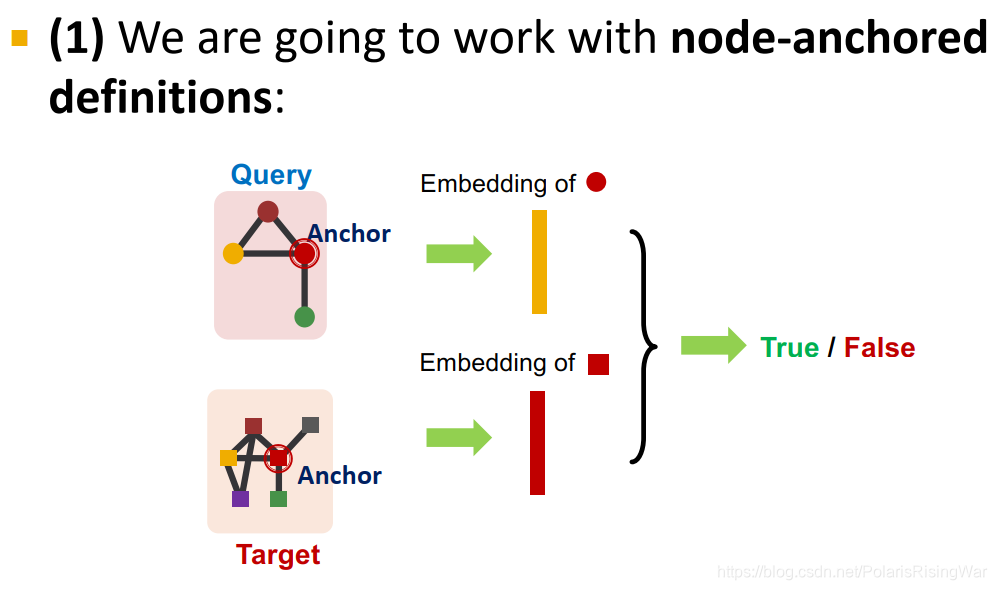
- 使用node-anchored neighborhoods:
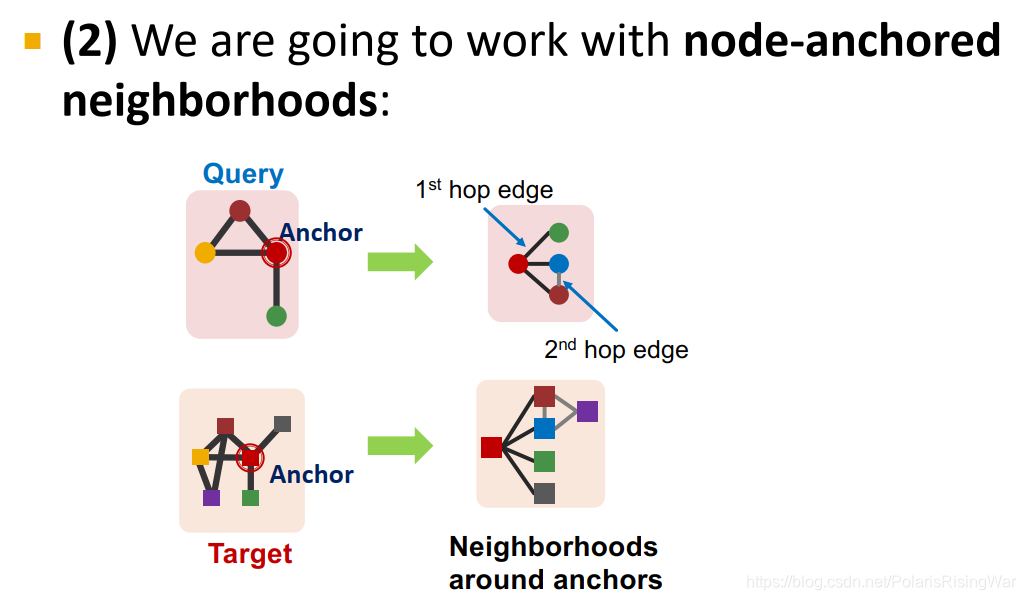
上图中应该是把右图的黄色点画成蓝色了
用GNN基于anchor的邻居得到其嵌入,预测 u u u 的邻居是否与 v v v 的邻居同构(图中应该是用了二阶邻居的意思):
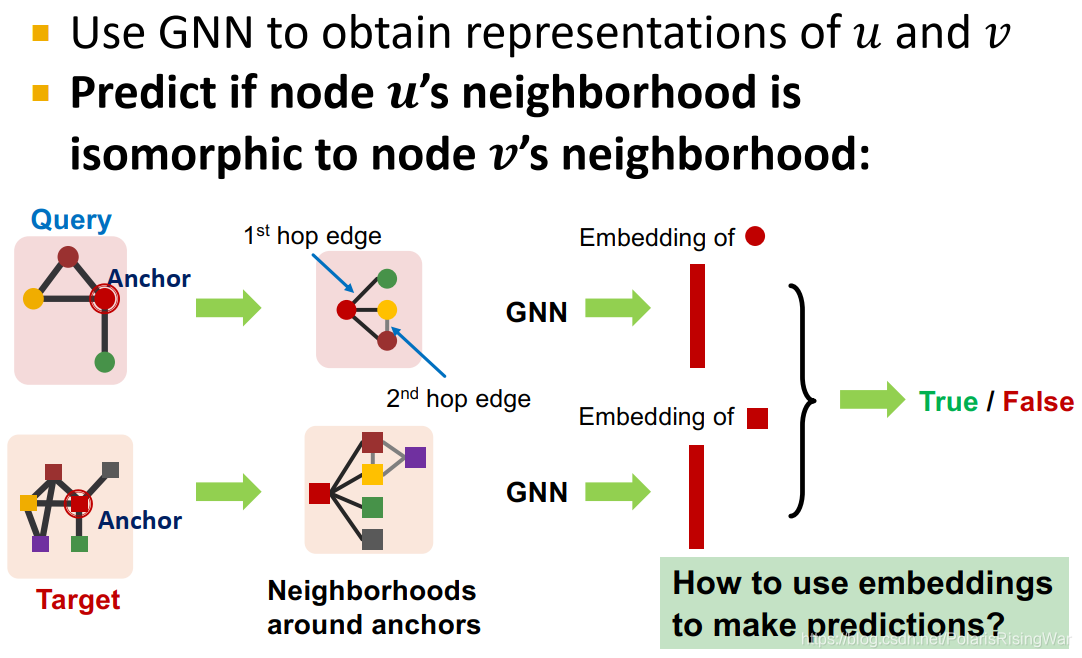
- 我们将使用node-anchored定义,用anchor的嵌入来判断是否同构
-
为什么要使用anchor呢?
回忆node-level frequency definition。这是因为我们可以用GNN来获得 u u u 和 v v v 对应的嵌入,从而可以得知 u u u 的邻居是否与 v v v 的邻居同构,这样就可以预测是否存在anchor的映射关系并识别出对应的特定节点。

-
将 G T G_T GT? 分解为neighborhoods:
对 G T G_T GT? 中的每个节点(准anchor),获取其k跳邻居(可以通过BFS获取)。k是一个超参,k越大,模型代价越高。
同样的过程也应用于 G Q G_Q GQ?,同样得到neighborhoods。
我们通过GNN得到anchor node基于neighborhood的embedding,也就是得到了这些neighborhoods的嵌入。

-
order embeddings space
将图 A A A 映射到高维(如64维)嵌入域的点 z A z_A zA?,使 z A z_A zA? 所有维度元素都非负。
可以捕获partial ordering(关系可传递)(具体见图):

总之可以用嵌入各维元素全部小于等于的关系来表示subgraph9 -
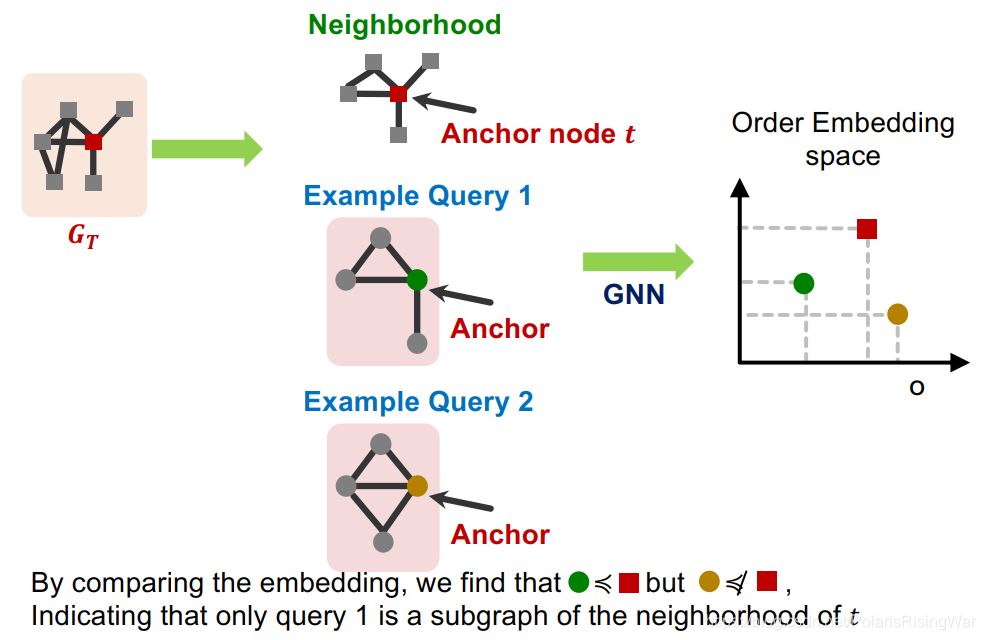
subgraph order embedding space
如图:在order embedding space中全部维度小于target graph的anchor嵌入的就是其subgraph的anchor嵌入(在二维嵌入域中,就是在target graph的左下角)
-
为什么要使用order embedding space?
因为subgraph isomorphism relationship可以很好地在order embedding space中编码,也就是说order embedding可以在向量域表示图域中subgraph的关系:
transitivity:
?图域:如果 G 1 G_1 G1? 是 G 2 G_2 G2? 的subgraph, G 2 G_2 G2? 是 G 3 G_3 G3? 的subgraph,则 G 1 G_1 G1? 是 G 3 G_3 G3? 的subgraph
?嵌入域:(见图)
anti-symmetry:
?图域:如果 G 1 G_1 G1? 是 G 2 G_2 G2? 的subgraph, G 2 G_2 G2? 是 G 1 G_1 G1? 的subgraph,则 G 1 G_1 G1? 与 G 2 G_2 G2? 同构。
?嵌入域:(见图)
closure under intersection:
?图域:1个节点的图是所有图的subgraph
?嵌入域:(见图)

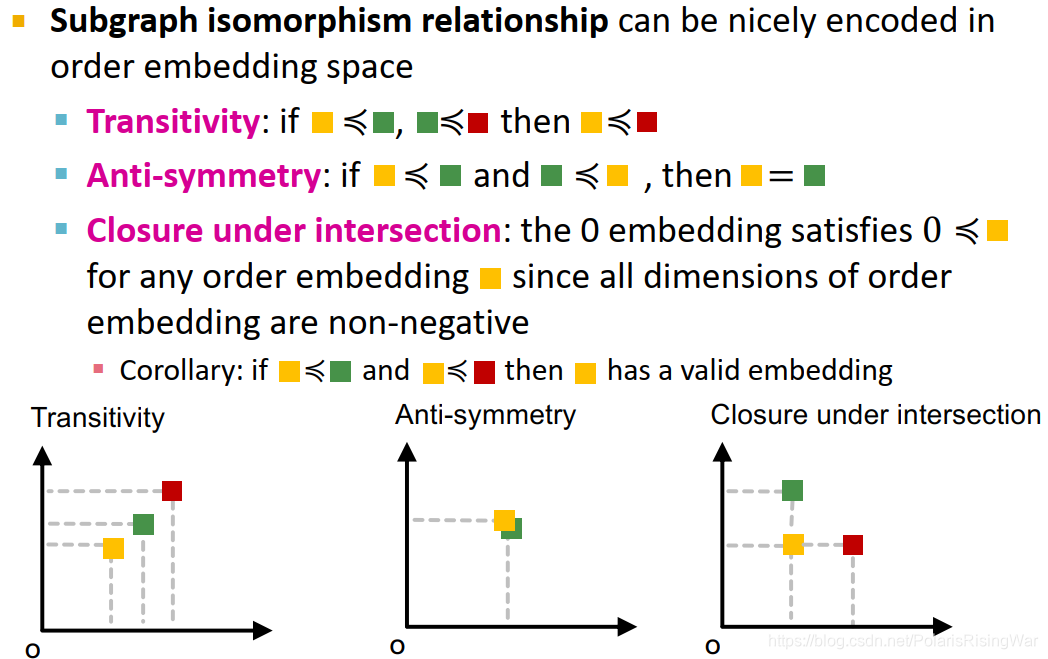
Corollary推论(必然的结果(或结论);)13
这个valid embedding是啥东西我就没看懂 -
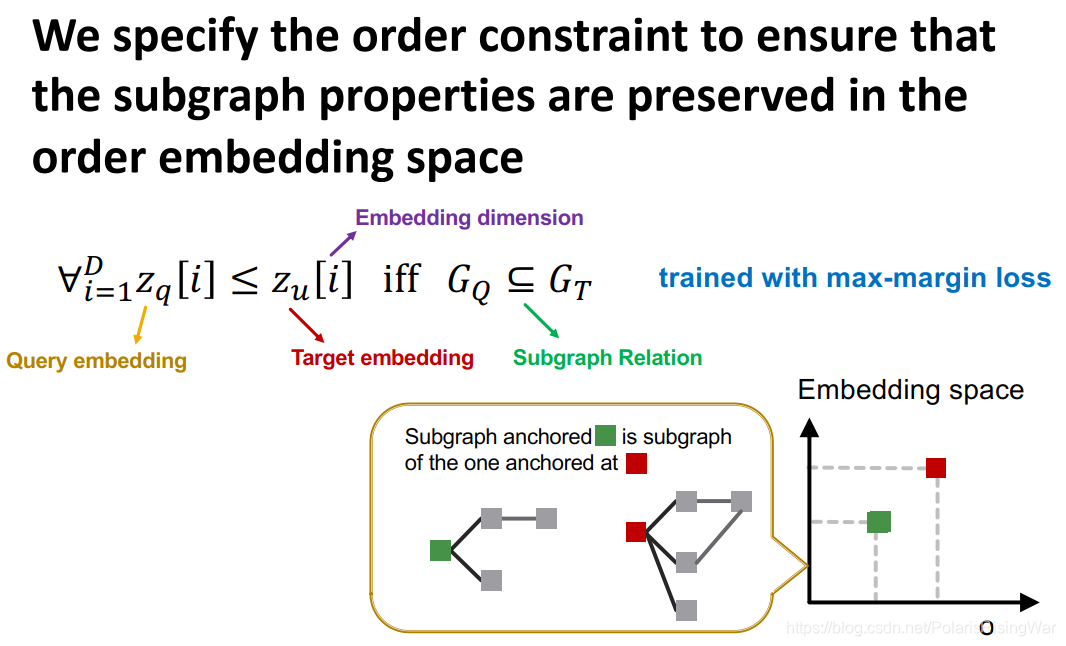
order constraint
我们用GNN来嵌入neighborhoods并保持其order embedding结构,因此我们需要学习一种可以学习反映subgraph关系的order embedding的损失函数。
我们基于order constraint设计损失函数。order constraint规定了理想的可反映subgraph关系的order embedding属性:
? i = 1 D z q [ i ] ≤ z u [ i ] ?iff? G Q ? G T \forall_{i=1}^Dz_q[i]\leq z_u[i]\ \text{iff}\ G_Q\subseteq G_T ?i=1D?zq?[i]≤zu?[i]?iff?GQ??GT?
其中 z q z_q zq? 是query embedding, z u z_u zu? 是target embedding, i i i 是embedding dimension(D应该是嵌入维度), ? \subseteq ? 是subgraph关系。
order constraint用max-margin loss14 来训练。

-
损失函数
GNN嵌入通过最小化max-margin loss学得。
定义 E ( G q , G t ) = ∑ i = 1 D ( max ? ( 0 , z q [ i ] ? z t [ i ] ) ) 2 E(G_q,G_t)=\sum_{i=1}^D\big(\max(0,z_q[i]-z_t[i])\big)^2 E(Gq?,Gt?)=∑i=1D?(max(0,zq?[i]?zt?[i]))2 为图 G q G_q Gq? 和 G t G_t Gt? 之间的margin(penalty或violation)。
当margin=0时 z q [ i ] ? < ? z t [ i ] z_q[i]\ <\ z_t[i] zq?[i]?<?zt?[i] 恒成立,即 G q G_q Gq? 是 G t G_t Gt? 的subgraph;当margin>0时 G q G_q Gq? 不是 G t G_t Gt? 的subgraph。


-
training neural subgraph matching
为了学习这种嵌入,需要约束训练集样本 ( G q , G t ) (G_q,G_t) (Gq?,Gt?) 中一半 G q G_q Gq? 是 G t G_t Gt? 的subgraph,另一半不是。
对正样本:最小化 E ( G q , G t ) E(G_q,G_t) E(Gq?,Gt?)
对负样本:最小化 max ? ( 0 , α ? E ( G q , G t ) ) \max\big(0,\alpha-E(G_q,G_t)\big) max(0,α?E(Gq?,Gt?))
max-margin loss使正样本中 z q [ i ] ? < ? z t [ i ] z_q[i]\ <\ z_t[i] zq?[i]?<?zt?[i],使全式为0;负样本中的 E ( G q , G t ) E(G_q,G_t) E(Gq?,Gt?) 大于 α \alpha α(使 α ? E ( G q , G t ) \alpha-E(G_q,G_t) α?E(Gq?,Gt?) 小于0,使全式为0)。但都不强化其差异,使嵌入向量之间不需要隔很远(slides中说这是degenerate strategy,我也没查到这又是个啥东西)

-
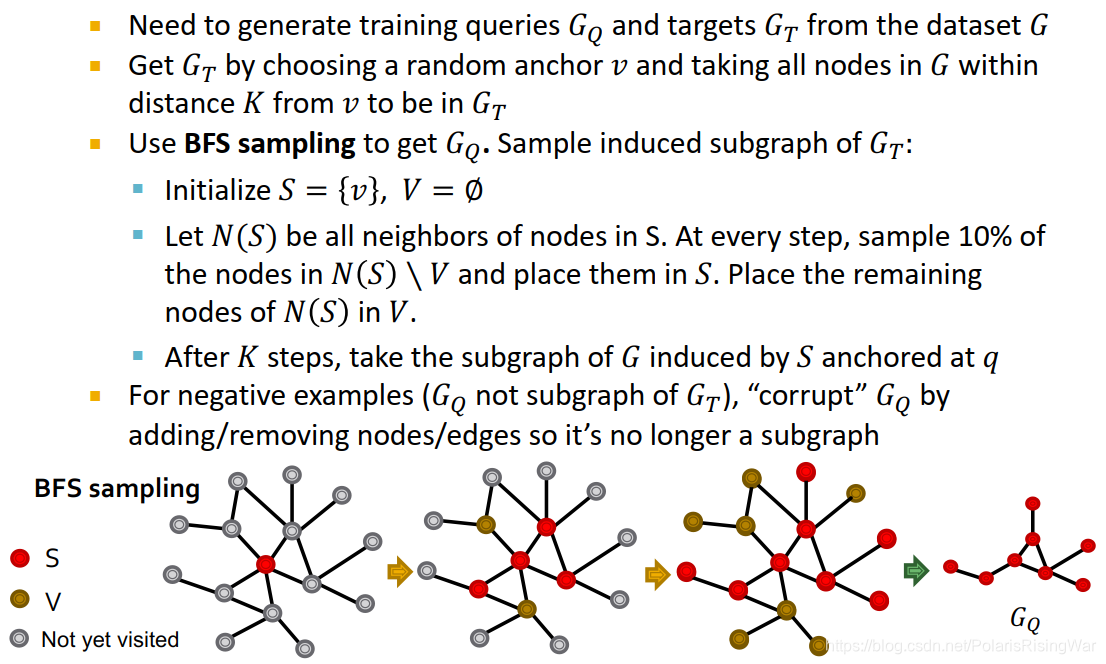
training example construction
我们需要从数据集 G G G 中生成训练样本:query G Q G_Q GQ? 和target G T G_T GT?
得到 G T G_T GT?:随机选取anchor v v v,获取其全部 K K K 阶邻居。
得到 G Q G_Q GQ?:用BFS抽样,从 G T G_T GT? 中抽样induced subgraph:
?step1:初始化 S = { v } , V = ? S=\{v\},V=\varnothing S={v},V=?
?step2:使 N ( S ) N(S) N(S) 为 S S S 中节点的所有邻居。每一步抽样10%在 N ( S ) \ V N(S)\backslash V N(S)\V 中的节点放入 S S S 中,并将其余节点放在 V V V 中。
?step3: K K K 步后,获取 G G G 的 induced by S S S anchored at q q q 的subgraph
对负样本( G Q G_Q GQ? 不是 G T G_T GT? 的subgraph):corrupt G Q G_Q GQ?:增加/移动节点/边使它不再是一个subgraph
-
训练细节
- 我们需要抽样出多少training examples?
每次迭代,我们都需要抽样新的target-query对。
这样做的好处是每次模型都会看到不同的subgraph例子,提升表现结果、避免过拟合(毕竟有指数级的可能subgraph可供抽样) - BFS抽样应该多深?
这是一个需要平衡运行时间和表现结果的超参数,一般设置为3-5,也需要取决于数据集的大小。

- 我们需要抽样出多少training examples?
-
在新图上预测一个图是否是另一个图的subgraph
已知:query graph G q G_q Gq? anchored at node q q q, target graph G t G_t Gt? anchored at node t t t
目标:输出query是否是target的node-anchored subgraph
过程:如果 E ( G q , G t ) < ? E(G_q,G_t)<\epsilon E(Gq?,Gt?)<?,预测为真;反之预测为假( ? \epsilon ? 是超参数)
为了检验 G Q G_Q GQ? 是否与 G T G_T GT? subgraph isomorphism,对所有 q ∈ G Q , t ∈ G T q\in G_Q,t\in G_T q∈GQ?,t∈GT? 重复上述流程。此处的 G q G_q Gq? 是 q ∈ G Q q\in G_Q q∈GQ? 附近的neighborhood。

-
neural subgraph matching总结
neural subgraph matching使用基于机器学习的方法学习NP-hard的subgraph isomorphism问题:
?1. 将query和target图都嵌入order embedding space
?2. 用这些嵌入向量计算 E ( G q , G t ) E(G_q,G_t) E(Gq?,Gt?) 以判断query是否是target的subgraph
用order embedding space嵌入图使subgraph isomorphism可以高效表示并由图嵌入的相对位置进行检验。

4. Mining / Finding Frequent Motifs / Subgraphs
- finding frequent subgraphs
找最频繁的大小为k的motif需要解决两个挑战:- 迭代所有大小为k的connected subgraph
- 数每一类subgraph的出现次数
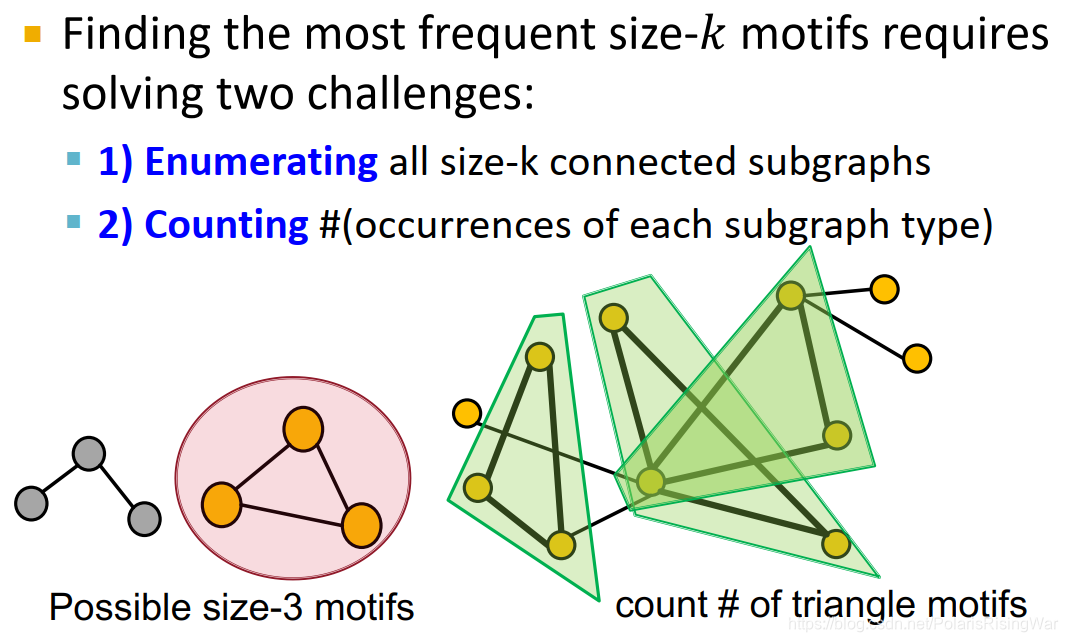
- 这个问题难在仅确定一个特定subgraph是否存在于图中就已是计算代价很高的问题(subgraph isomorphism是NP-complete),计算用时随subgraph指数级增长(因此传统方法可行的motif尺寸都相对较小,如3-7)。
可以说这是两个指数级增长的问题梦幻联动(特定大小有多少motif(组合爆炸combinatorial explosion15)+找出每个motif的frequency(subgraph isomorphism and subgraph counting))

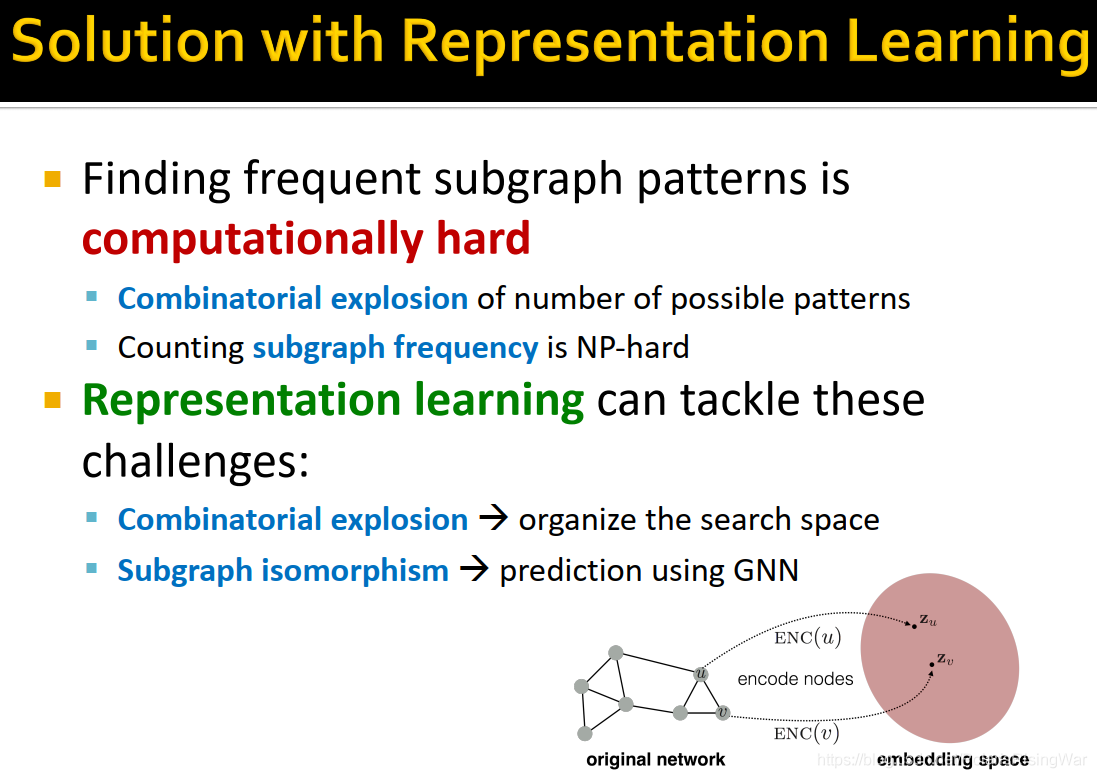
- 使用表示学习的方法来解决问题
表示学习通过search space(每次增加一个节点,累积到size k的subgraph上,详情见下文。注意我们仅关心高频subgraph)解决组合爆炸问题,通过GNN预测解决subgraph isomorphism问题(就是本章第三节所讲述的知识)。

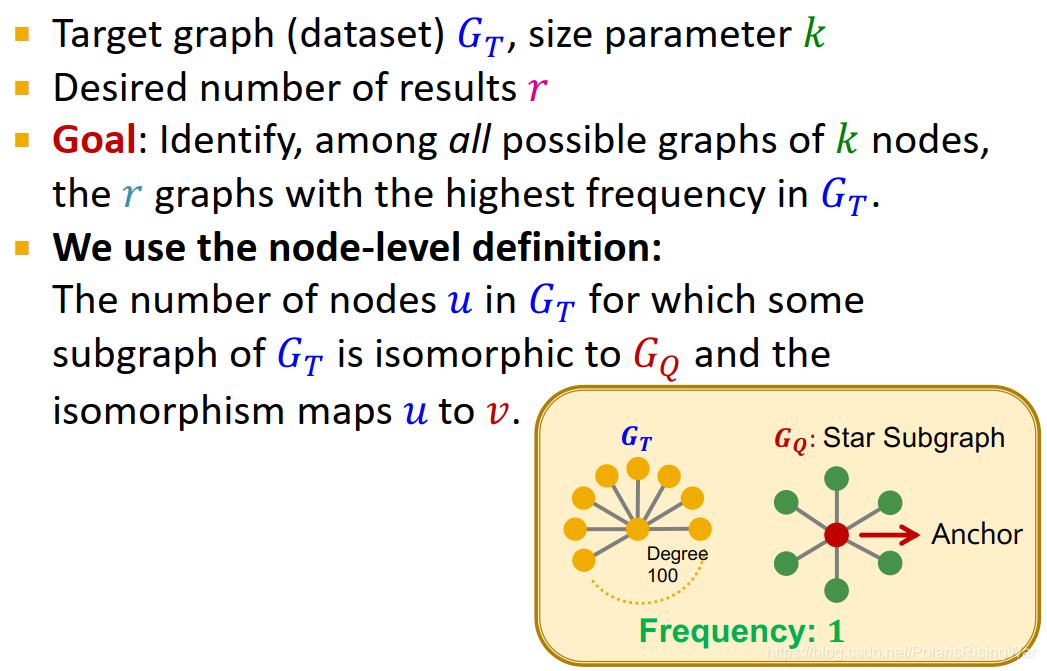
- problem setup: frequent motif mining
给出target graph(数据集) G T G_T GT?,subgraph大小参数 k k k
所需结果数量 r r r
目标:从所有大小为 k k k 个节点的图中,识别出 r r r 个在 G T G_T GT? 中出现频率最高的图。
我们使用node-level subgraph定义。
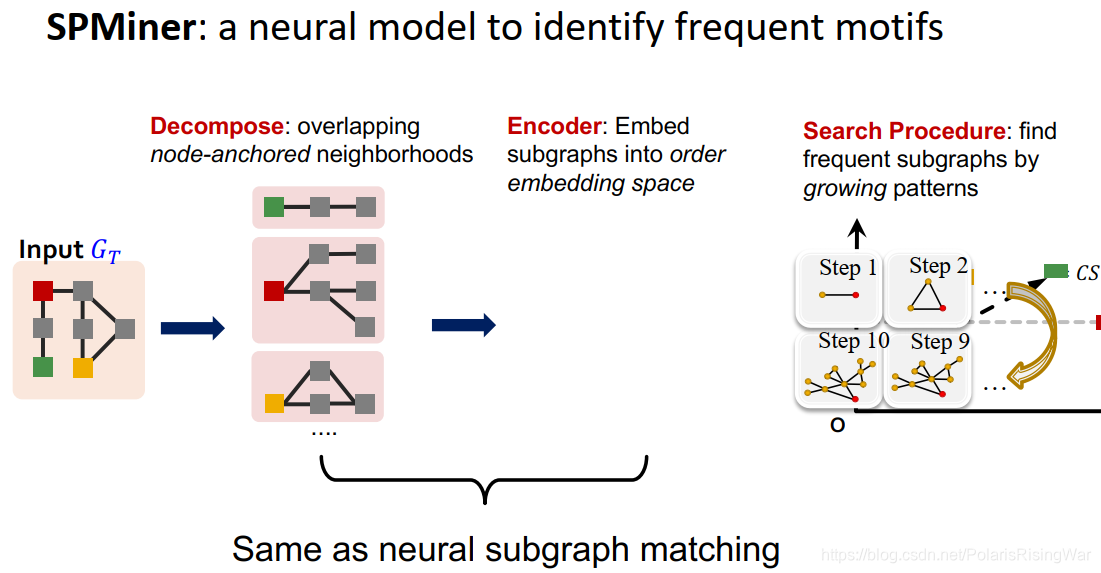
- SPMiner overview
SPMiner:识别高频motifs的神经网络模型
步骤:将输入图 G T G_T GT? decompose为重复的node-anchored neighborhoods,将subgraph嵌入到order embedding space(上述两步和neural subgraph matching是一样的);然后进行search procedure,策略是不遍历所有可能的subgraph,而直接从2个节点的图开始增长出一个所需节点数的subgraph,在增长的同时尽量保证频率高。
- SPMiner:核心思想

order embedding的核心优势:可以迅速找到特定subgraph G Q G_Q GQ? 的频率

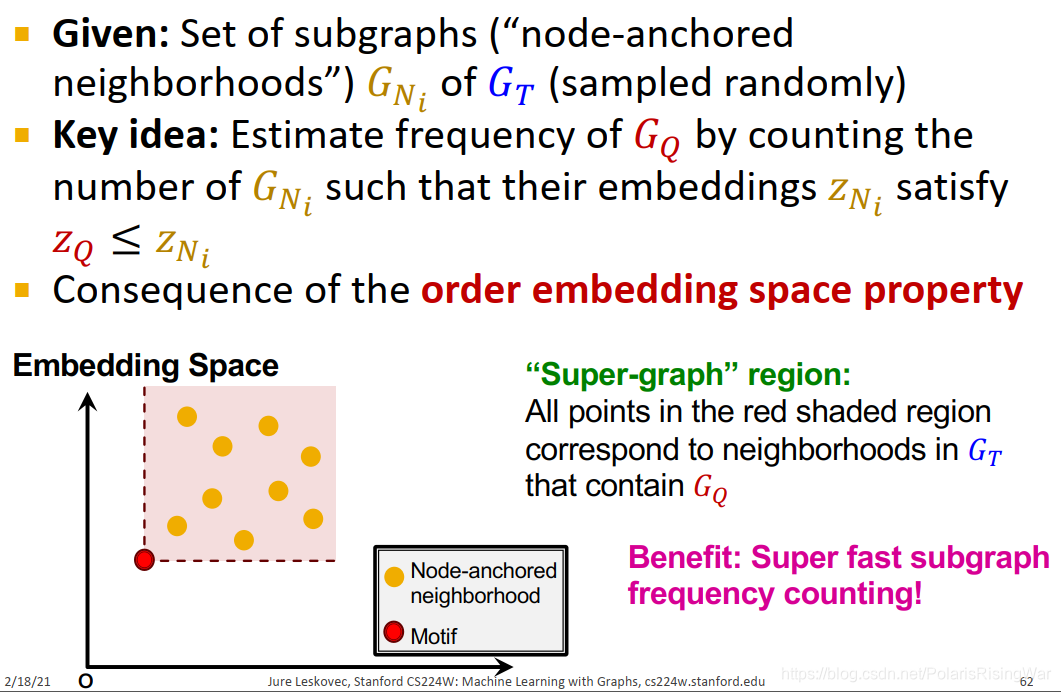
- motif频率估计
已知:一系列 G T G_T GT? 的subgraph(node-anchored neighborhoods) G N i G_{N_i} GNi?? (通过随机抽样得到)。
核心思想:估计 G Q G_Q GQ? 的频率:通过数符合要求的 G N i G_{N_i} GNi?? 的个数( z Q ≤ z N i z_Q\leq z_{N_i} zQ?≤zNi??)
这是由order embedding space的属性得到的结论:如下图所示,红色节点(motif)右上角的红色区域就是其super-graph region,红色节点是所有落在该区域的节点( G T G_T GT? 的neighborhoods)的subgraph。
这样的好处就是算得快。
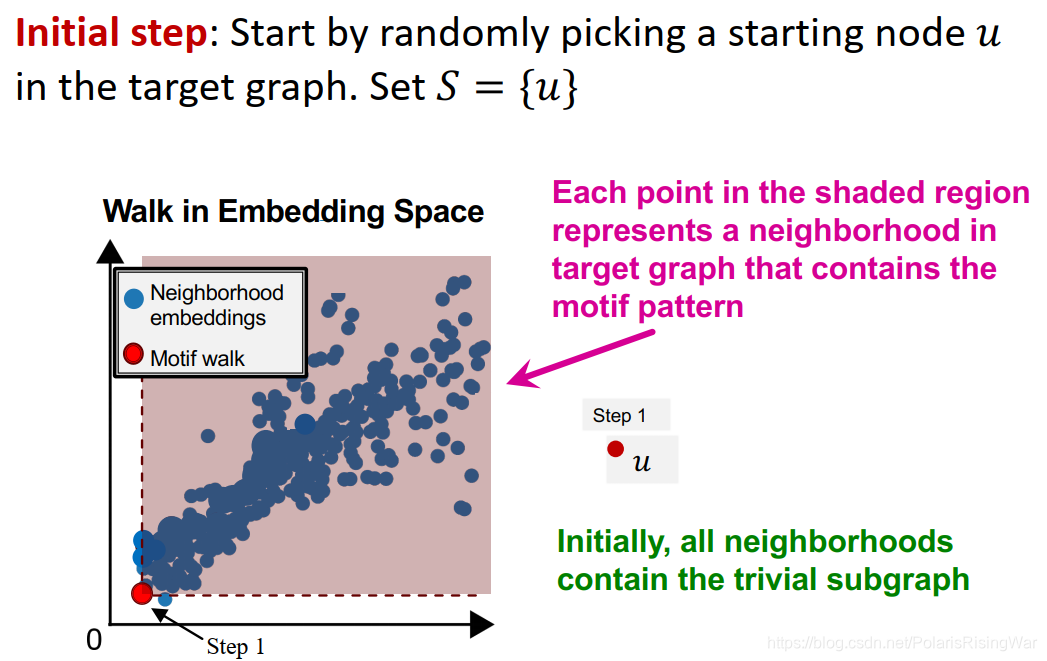
- SPMiner search procedure
- 开始:从一个从target graph中随机选择的起点
u
u
u 开始:设
S
=
{
u
}
S=\{u\}
S={u}
所有neighborhoods都在一个点的右上方区域,即都包含这个subgraph。
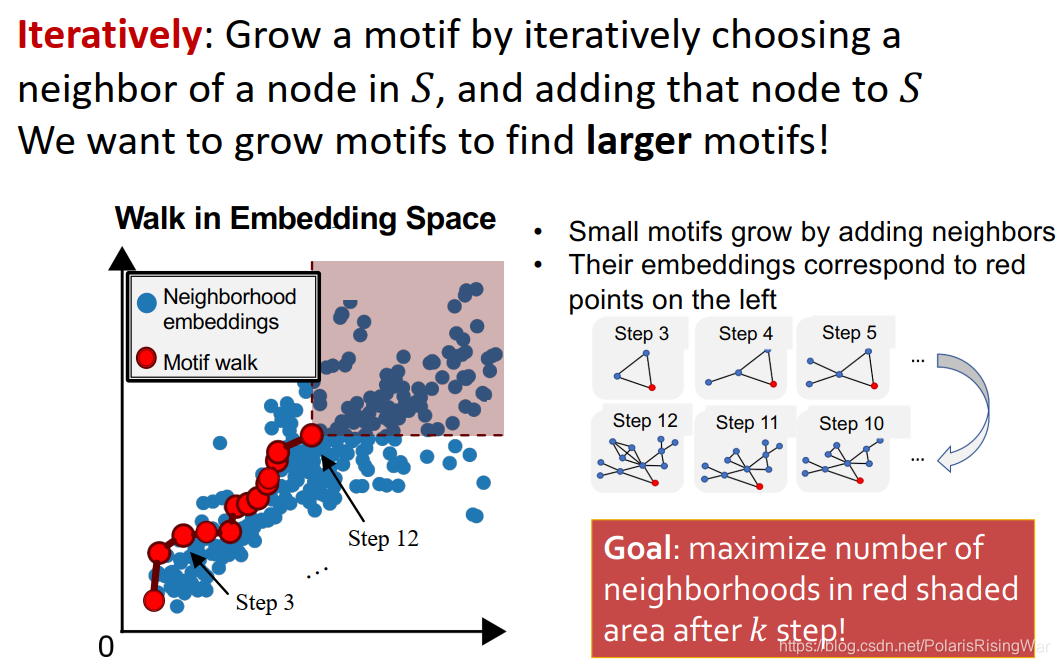
- 迭代:每次选一个
S
S
S 中节点的邻居,加到
S
S
S 中,如此逐渐增长motif的尺寸。
目标:在 k k k 步后最大化红色阴影区域中的neighborhoods数目。
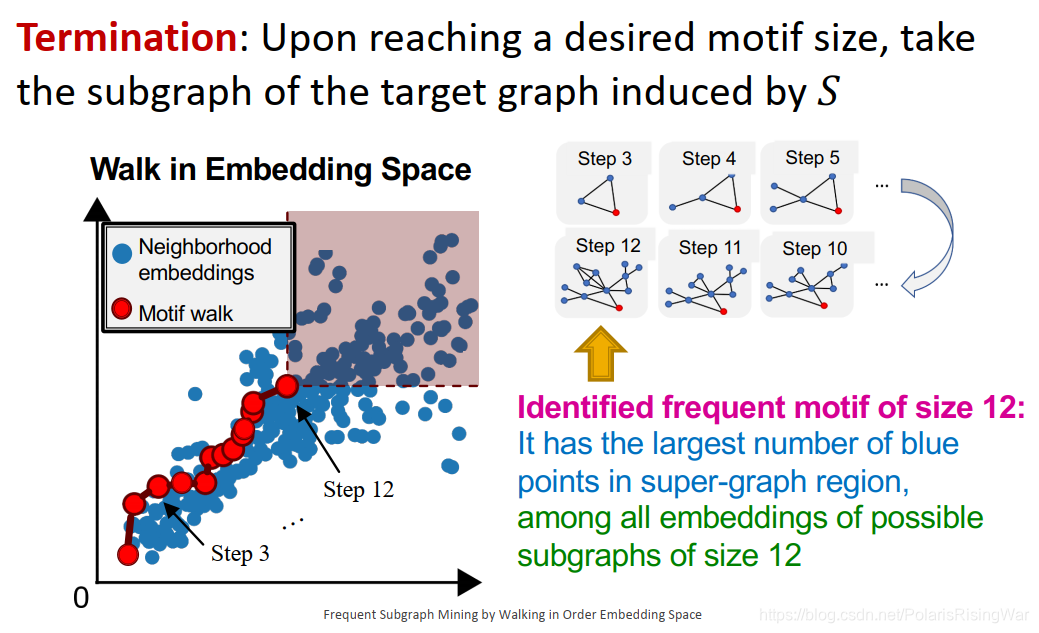
- 停止:达到预期motif尺寸后,选取the subgraph of the target graph induced by
S
S
S
我们找到的motif就是预期尺寸备选subgraph嵌入中有最多target graph neighborhoods(蓝点)在红色区域的subgraph。
- 每一步如何选取节点?
定义subgraph G G G 的total violation:不包含 G G G 的neighborhoods数量。即不满足 z Q ? z N i z_Q\preccurlyeq z_{N_i} zQ??zNi?? 的neighborhoods G N i G_{N_i} GNi?? 数量。
最小化total violation就是最大化频率。
我们采用贪心算法,每一步都选择时当前total violation最小的节点。
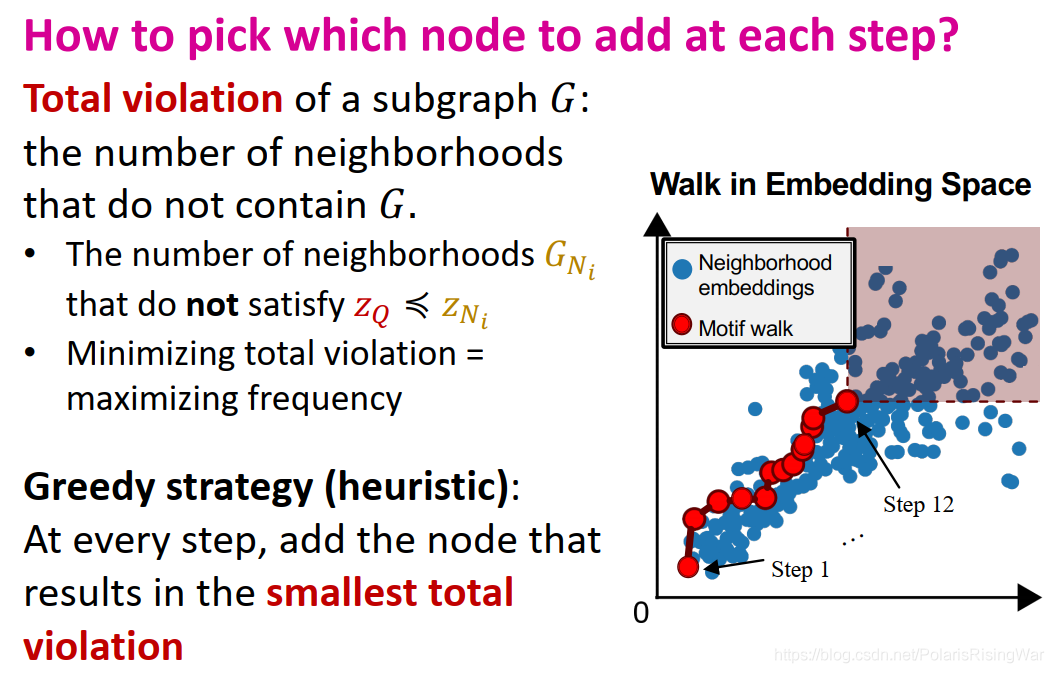
- 开始:从一个从target graph中随机选择的起点
u
u
u 开始:设
S
=
{
u
}
S=\{u\}
S={u}
- 实验结果
- 小motif
ground truth:通过代价高昂的BF迭代算法(暴力破解)找到10个出现频率最高的motif。
在大小为5-6的motif上,SPMiner可以识别出top 10中前9/8个,识别出的频率接近真实值:
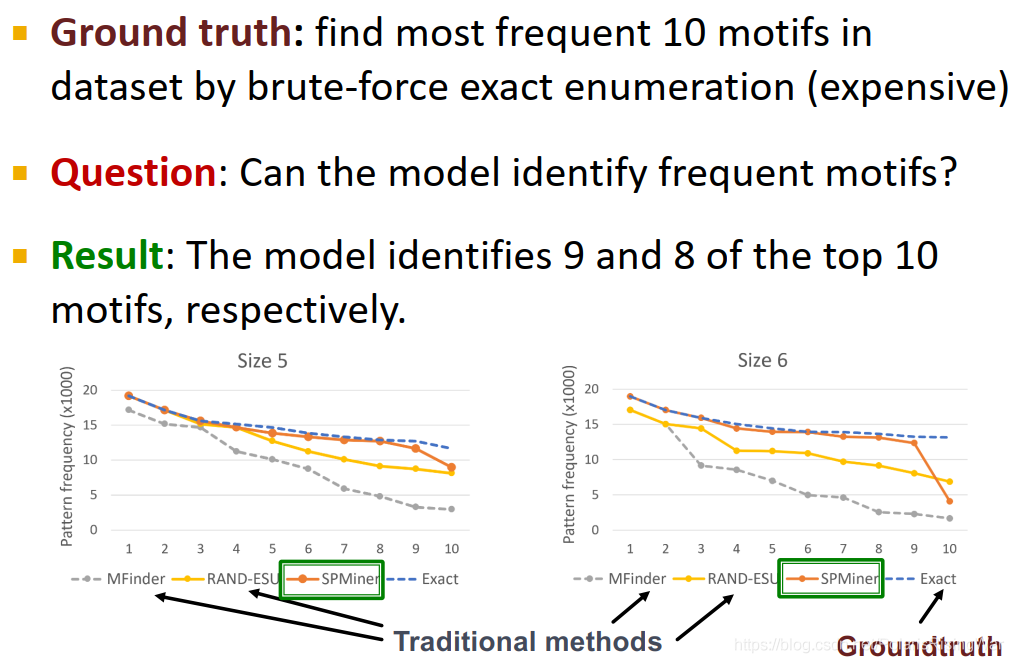
- 大motif
SPMiner比baseline多识别10-100倍。
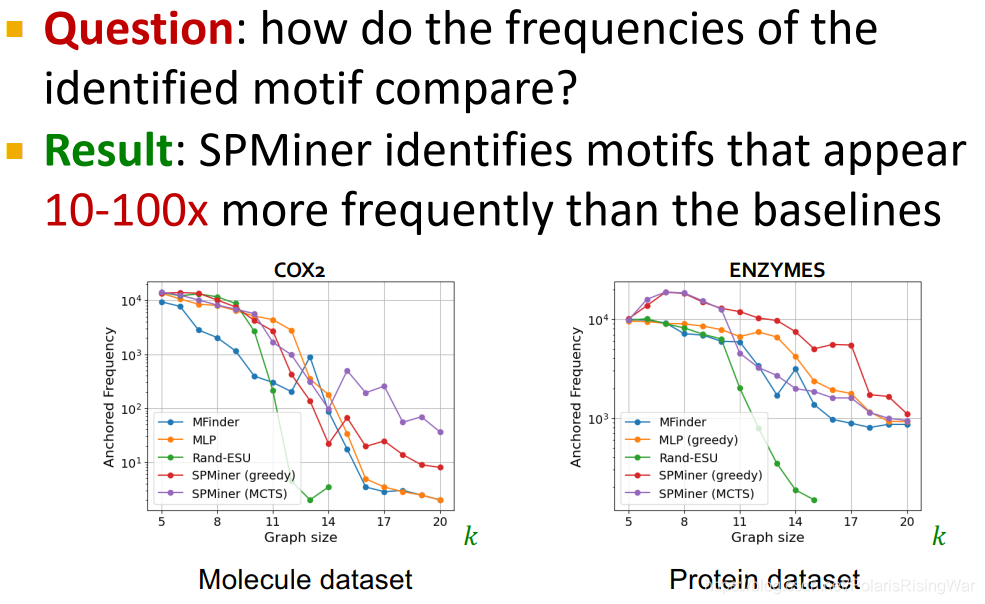
- 小motif
- 总结
- subgraph和motif是可用于深入了解图结构的重要概念,对其计数可用作节点或图的特征。
- 本章介绍一种预测subgraph isomorphism关系的神经网络方法。
- order embeddings的特性可用于编码subgraph关系。
- order embedding space上的neural embedding-guided search让我们有了一种比传统方法能识别出更高motif频率的机器学习模型。

我直接用百度查这个关键词没查到,只查到说离散数学中有matching problem(参考这篇文章:离散数学笔记6(Matching problems) - 知乎 ),但是感觉这个跟本章内容没什么关系?
所以我觉得原文指的应该是传统的subgraph matching方法11。对于这些传统的subgraph matching方法我没有做过了解,我就是直接学的本章课程。 ??Edge-induced subgraph | Article about edge-induced subgraph by The Free Dictionary 说edge-induced subgraph中的节点是全部在其边中出现过至少一次的原图节点。
Edge-Induced Subgraph – from Wolfram MathWorld: An edge-induced subgraph is a subset of the edges of a graph G together with any vertices that are their endpoints7.
子图的概念_yyywww666的专栏-CSDN博客
networkx.classes.function.edge_subgraph — NetworkX 2.5 documentation
dgl.edge_subgraph — DGL 0.6.1 documentation ??看图上原句……呃,不知道有没有理解并翻译正确。
不过我觉得这点正误小问题不重要吧。
presence一词不知道在此处有无专业术语层面的引申义存在。 ??可参考 基因调控网络 (Gene Regulatory Network) 01 - Bracer - 博客园
因为不是我的专业领域,所以我没仔细看。 ?? ??我之前写的笔记:cs224w(图机器学习)2021冬季课程学习笔记2: Traditional Methods for ML on Graphs_诸神缄默不语的博客-CSDN博客 中脚注4 ??
当时我做这笔记的时候还能上英文维基,但是现在暂时不能了,所以我就把我当时用的参考资料列出来,具体内容只能看我之前笔记了,我没法再去原网页看一眼以作证实了:
① 一对节点之间连了多个边 来源:https://zh.wikipedia.org/wiki/%E9%87%8D%E8%BE%B9
② https://en.wikipedia.org/wiki/Dual_graph ??一条边的endpoint就是其对应的两个端点。无论有向还是无向都是两个端点。
参考自OI Wiki。
原话: 图源:图论相关概念 - OI Wiki ?? ??
图源:图论相关概念 - OI Wiki ?? ??所以这个玩意居然能收敛吗也是很神奇 ??
这个好像挺复杂的,我也没仔细看。
链接反正也发出来,以资参考:Networks based on words ??我在之前查到的对subgraph matching问题的定义:给出target graph和query graph,确定query graph是否是target graph的子图,如是确定其位置。参考16)
其他可参考定义及来源:
Subgraph matching problem is identifying a target subgraph in a graph. 来自 Subgraph Matching Using Graph Neural Network ?? ??我并没有这样的直觉,也没看懂这句话啥意思。 ??
可以参考:区分定理(Theorem)、引理(Lemma)、推论(Corollary)等概念_cloudeagle_bupt的专栏-CSDN博客_corollary ??
我是感觉max margin在网上我找到的定义跟这边这个不太一样啊……在这边的话就按照课程中讲的来吧。
我在网上了解该概念所使用的资料也放出来,以资参考:损失函数:Hinge Loss(max margin) - 菜鸡一枚 - 博客园 ??其实我没看懂组合爆炸这个词是啥意思……就我能理解它随着size变大,subgraph变多,这件事。但是组合爆炸这个词本身是啥意思,我就没搞懂。
我在stack overflow上看到了这样一个问题:Examples for combinatorial explosion in Java? - Stack Overflow 就是Java等编程语言里面的组合爆炸,这个我能看得懂,就……我也是程序员,我也是解耦人啊,我怎么能不懂interface的意义!
但是这跟subgraph又有什么关系? ??原文:Subgraph matching is the problem of determining the presence and location (s) of a given query graph in a large target graph. 来自 [2007.03092] Neural Subgraph Matching ??
