上一篇线性回归是连续的量,用的是梯度下降或者正规方程来求解。
这一篇讲 分类 离散的量。
判定边界
首先随便不管是什么参数θ,我们需要的是输入x之后只输出1或者0两个答案中的一个。这种要求的话一般要阶跃函数比较贴切。不过比起那种武断的分类,逻辑回归用的是概率,概率大于0.5则分类为1.也就是说,我们实际上还是输出0~1的连续的值【概率值】然后大于0.5的分类到1,小的分到0去。

客户端公式是h(x),输入x,输出分类到1的可能性。程序内部要给定θ的一系列值,然后实际函数用的是g(z)这个函数图像。总之θTx≥0时,预测分类为1.
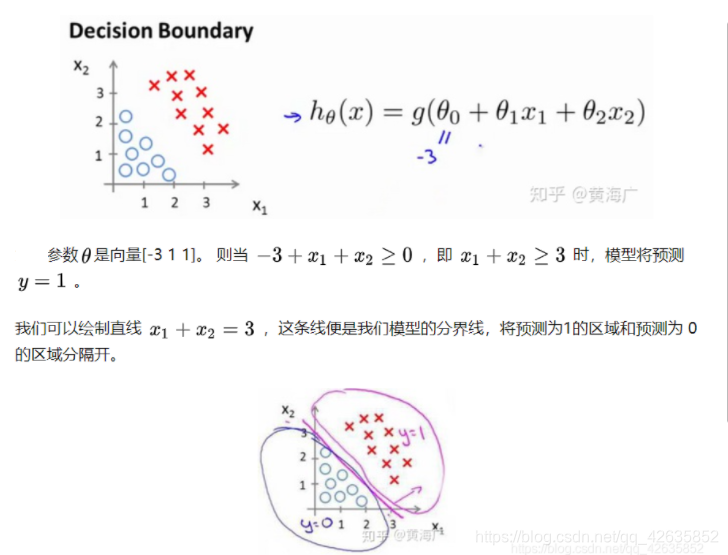
自己试一试怎么画出一个圆形的区域吧
代价函数
好,现在要开始让机器自动找合适的θ了
一个合适的θ,应该在理应分类为1的时候预测的h(x)输出为0.5~1 ,所以预测值越靠近0,代价越大。
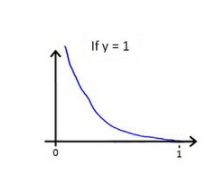
所以求代价的值就用这个公式
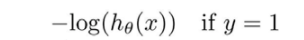
分类为0的情况得反一下,所以整个公式是
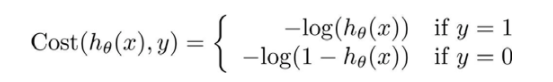
那么,每个样本的代价总和就是加起来除以数量取平均就是了,跟线性回归一样
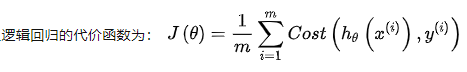
//之所以不像线性回归那样直接用( 预测值-分类值 )^2 是因为不合适,会有很多个局部最小值。
简化一下公式
利用1和0的特性做一做乘法,这样就只是一条公式,而不是分段函数
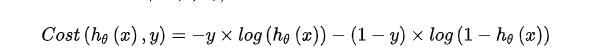
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。