1.累加累乘与积分

1.将向量下标为偶数的分量 (x2, x4, …) 累加, 写出相应表达式.
$\sum_{i=2n}^{n\in \mathbb{N}} x_i$
2.各出一道累加、累乘、积分表达式的习题, 并给出标准答案.
①将矩阵中大于等于1的分量平方并累加：
$\sum_{x_{ij}≥1}x_{ij}^2$
②将矩阵中不为0的分量累乘：
$\prod_{x_{ij}≠0}x_{ij}$
③函数 $x^3-x+2$ 在0到1上积分：
$\int_{0}^{1}x^3-x+2 \mathrm{d}x$
3.你使用过三重累加吗? 描述一下其应用.
在代码中三重循环算时间复杂度时会用到三重累加： $\sum_{i=1}^n\sum_{j=1}^i\sum_{k=1}^j l$
4.给一个常用的定积分, 将手算结果与程序结果对比.
定积分： $\int_{0}^{1}x^2+1 \mathrm{d}x$
手算结果： $\frac{4}{3}=1.33333...$
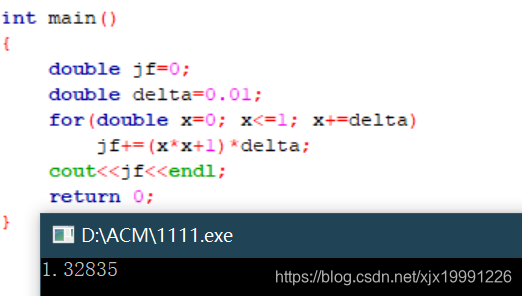
程序结果： $1.32835$ 在这里插入图片描述

2.线性回归

1.如何获得 $\mathbf{w}$ ?
推导过程:
$||\mathbf{Xw}-\mathbf{Y}||_2^2=(\mathbf{Xw}-\mathbf{Y})^T(\mathbf{Xw}-\mathbf{Y})=(\mathbf{w}^T\mathbf{X}^T-\mathbf{Y}^T)(\mathbf{Xw}-\mathbf{Y})=\mathbf{w}^T\mathbf{X}^T\mathbf{Xw}-\mathbf{w}^T\mathbf{X}^T\mathbf{Y}- \mathbf{Y}^T\mathbf{Xw}+\mathbf{Y}^T\mathbf{Y}$
将该式关于 $\mathbf{w}$ 求导 (使用向量求导法则) 并令其为 0, 可得
$\mathbf{X}^{\mathrm{T}}\mathbf{X} \mathbf{w} - \mathbf{X}^{\mathrm{T}}\mathbf{Y} = 0$
最后
$\mathbf{w} = (\mathbf{X}^{\mathrm{T}}\mathbf{X})^{-1}\mathbf{X}^{\mathrm{T}}\mathbf{Y}$
岭回归：
$\argmin_{\mathbf{w}}=||\mathbf{Xw}-\mathbf{Y}||_2^2-λ||\mathbf{w}||_2^2$
可推导出
$\mathbf{X}^{\mathrm{T}}\mathbf{X} \mathbf{w} - \mathbf{X}^{\mathrm{T}}\mathbf{Y} + \lambda \mathbf{w} = 0$
最后
$\mathbf{w} = (\mathbf{X}^{\mathrm{T}}\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^{\mathrm{T}}\mathbf{Y}$

2.自己写一个小例子 $(n = 3, m = 1)$ 来验证最小二乘法.
令函数 $y = 2 x + 1$ ;
$x$ 取值5,6,7， $\hat y$ 取值10,13,14
$\hat y=ax+b$ ,用最小二乘法求 $a, b$
$a=\frac{\sum_{i=1}^3x_i\hat y_i-3\overline{x}\overline{y}}{\sum_{i=1}^3x_i^2-3\overline x^2}=2.028$
$b=\overline{y}-a\overline{x}=0.132$

3.推导, 并描述这个方法的特点 (不少于 5 条).

$\argmax_\mathbf{w} L(x)=\prod_{i=1}^nP(y_i|\mathbf{x}_i; \mathbf{w})$

相乘计算困难, 将其求一个对数, 不改变单调性
$\log L(\mathbf{w}) = \sum_{i = 1}^n \log P(y_i \vert \mathbf{x}i; \mathbf{w}) = \sum{i = 1}^n y_i \log P(y_i = 1 \vert \mathbf{x}_i; \mathbf{w}) + (1 - y_i) \log(1 - P(y_i = 1 \vert \mathbf{x}i; \mathbf{w})) = \sum{i = 1}^n y_i \log \frac{P(y_i = 1 \vert \mathbf{x}_i; \mathbf{w})}{1 - P(y_i = 1 \vert \mathbf{x}_i; \mathbf{w})} + \log (1 - P(y_i = 1 \vert \mathbf{x}i; \mathbf{w})) = \sum{i = 1}^n y_i \mathbf{x}_i \mathbf{w} - \log (1 + e^{\mathbf{x}_i \mathbf{w}})$
对 $\mathbf{w}$ 求偏导
$\frac{\partial \log L(\mathbf{w})}{\partial \mathbf{w}} = \sum_{i = 1}^n y_i \mathbf{x}_i - \frac{e^{\mathbf{x}_i \mathbf{w}}}{1 + e^{\mathbf{x}_i \mathbf{w}}} \mathbf{x}i = \sum{i = 1}^n \left(y_i - \frac{e^{\mathbf{x}_i \mathbf{w}}}{1 + e^{\mathbf{x}_i \mathbf{w}}}\right) \mathbf{x}_i$
令该偏导为 0, 无法获得解析式, 因此用梯度下降.
$\mathbf{w}^{t+1}=\mathbf{w}^{t}-\alpha\frac{\partial \log L(\mathbf{w})}{\partial \mathbf{w}}$