我们要做的:
step 1:Function set
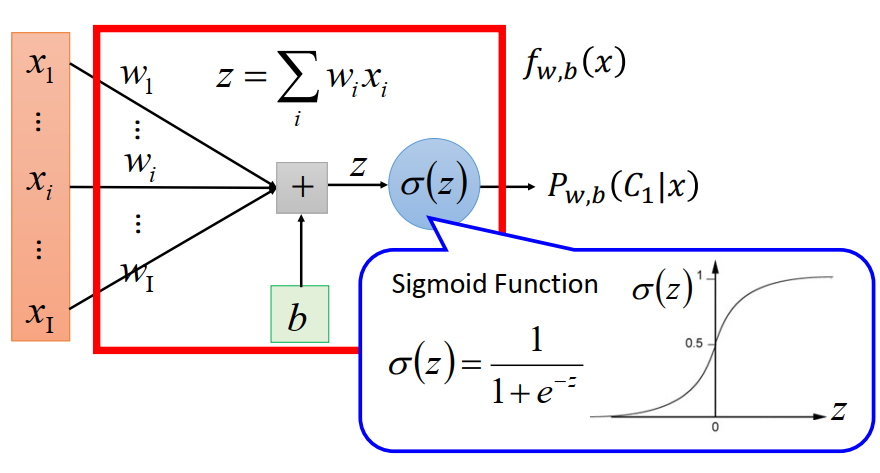
Step 2: Goodness of a Function

Step 3: Find the best function
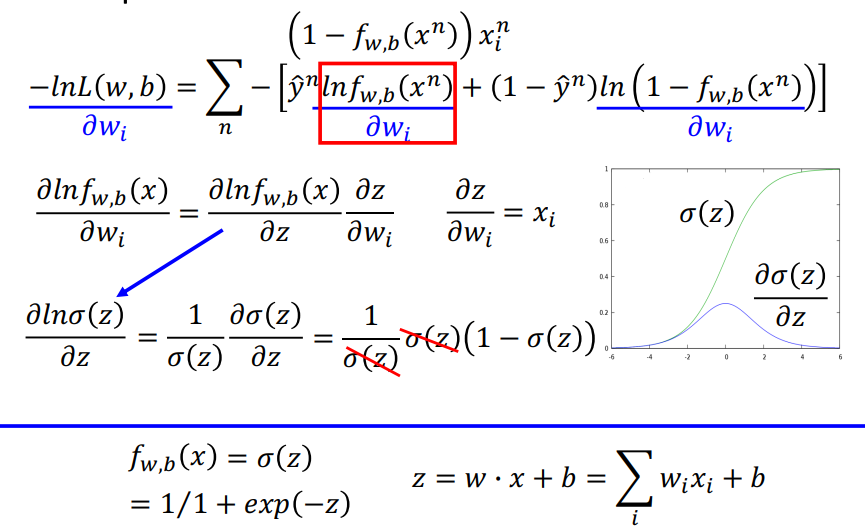
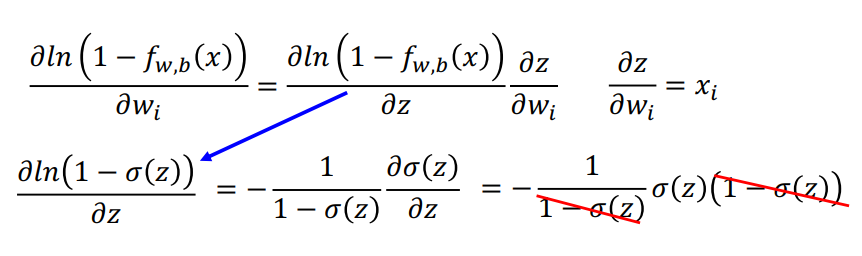
把两项 分别代入:
Logistic Regression VS Linear Regression

Logistic Regression + Square Error


Logistic Regression + Square Error
会出现距离目标很远 很近的时候微分算出来都是 0 。
如果选用Square Error这会造成很卡,离目标很远的时候,移动的速度是非常慢的。
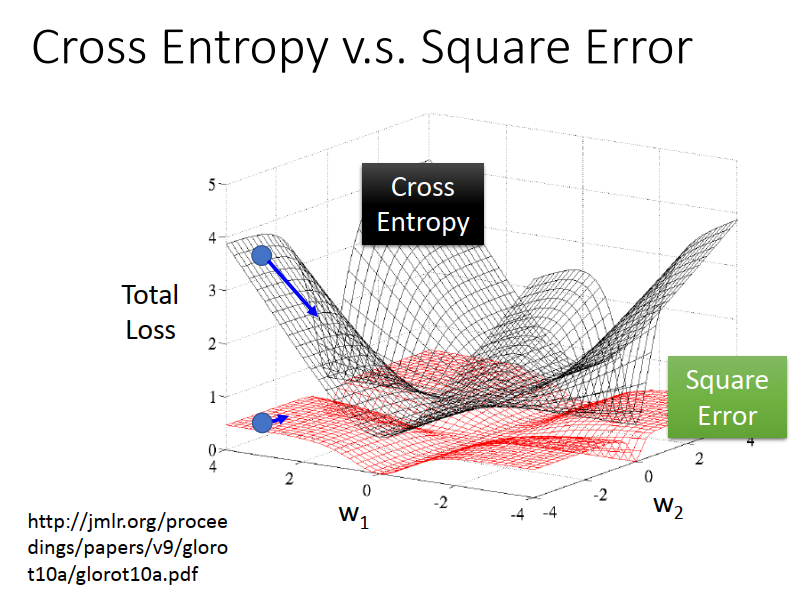
这个 Logistic Regression的方法,我们称它为Discriminative
之前用Gaussian来描述的方法,称为Generative
实际上他们的model 是一模一样的(但根据同一组training data 找出来的w 和b 是不一样的,因为做的假设不同(在Logistic Regression没有做任何假设,在Generative 是有假设的,假设它是Gaussian))

哪一个找出来的参数是比较好的呢?
Discriminative 是比较好的
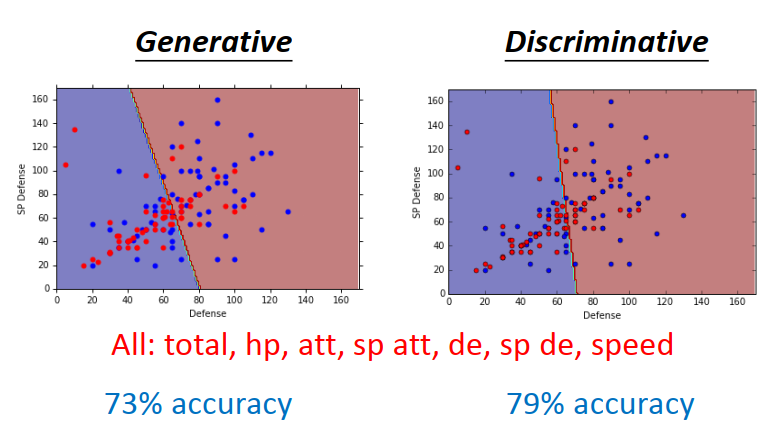
为什么会这样呢?
举个简单的例子:
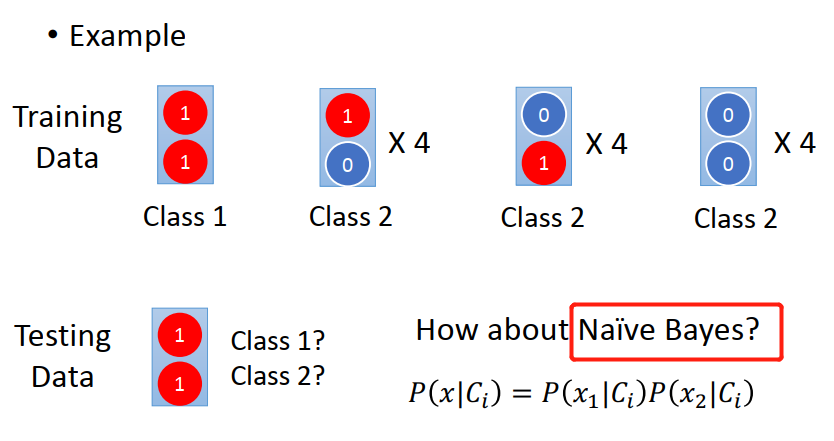
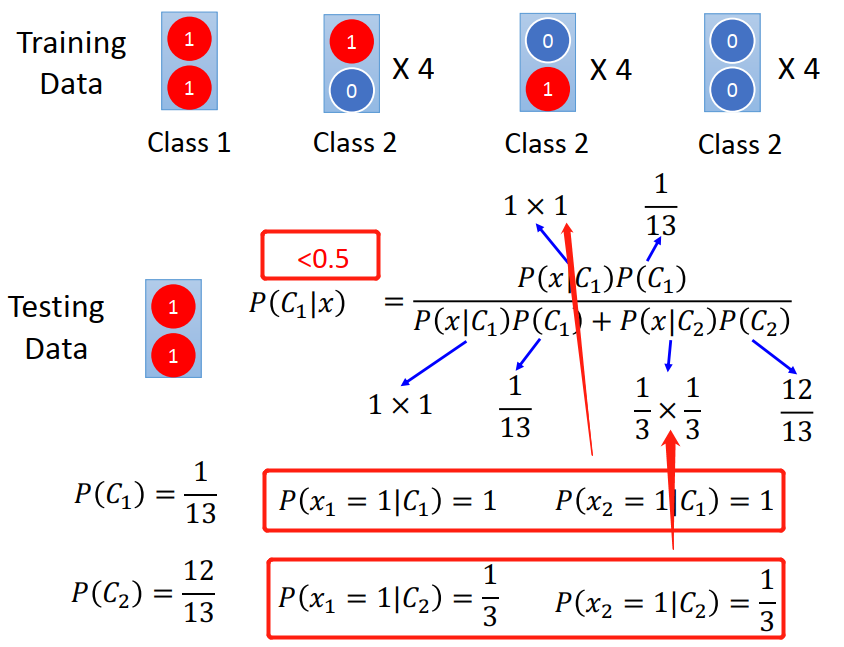
在naive Bayes中 Testing data中的“11” 被认为是class 2
Generative “脑补”了一下,它认为在class 2 中 可能会存在 “11”
? Benefit of generative model
? With the assumption of probability distribution, less training data is needed
? With the assumption of probability distribution,more robust to the noise
? Priors and class-dependent probabilities can be estimated from different sources.
在概率分布假设下,需要的训练数据较少
采用概率分布的假设,对噪声更有鲁棒性
先验和类相关的概率可以从不同的来源估计
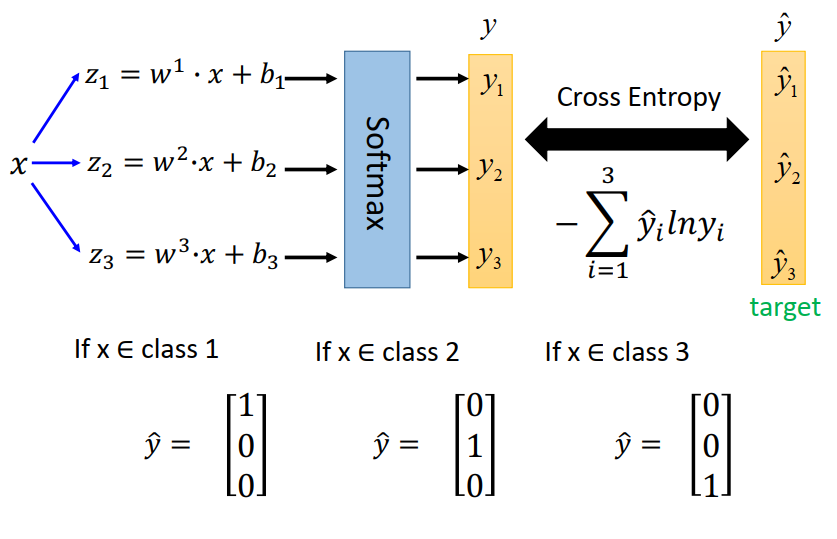
Multi-class Classificaation
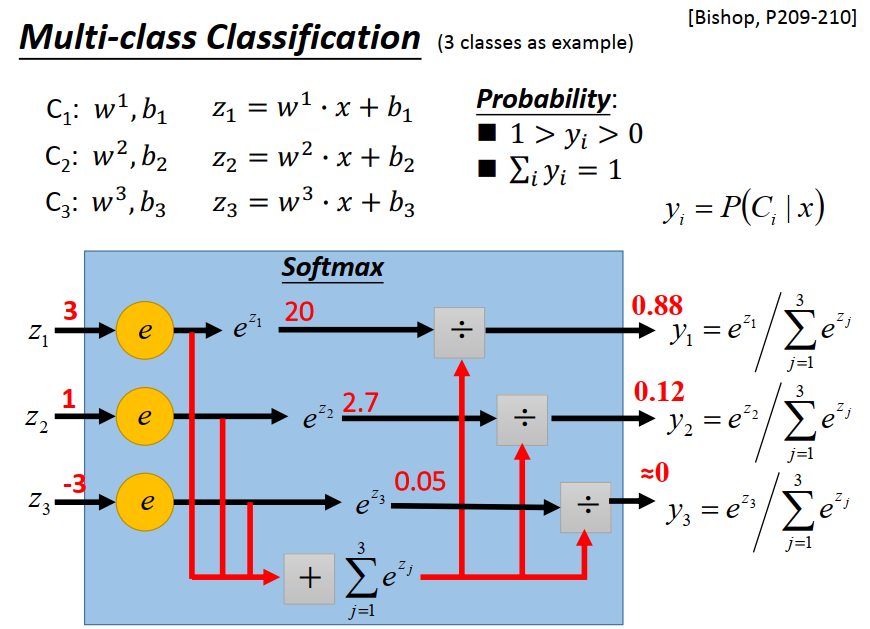
softmax的意义:对向量进行归一化,凸显其中最大的值并抑制远低于最大值的其他分量。
Logistic Regression 有非常大的限制。
例:
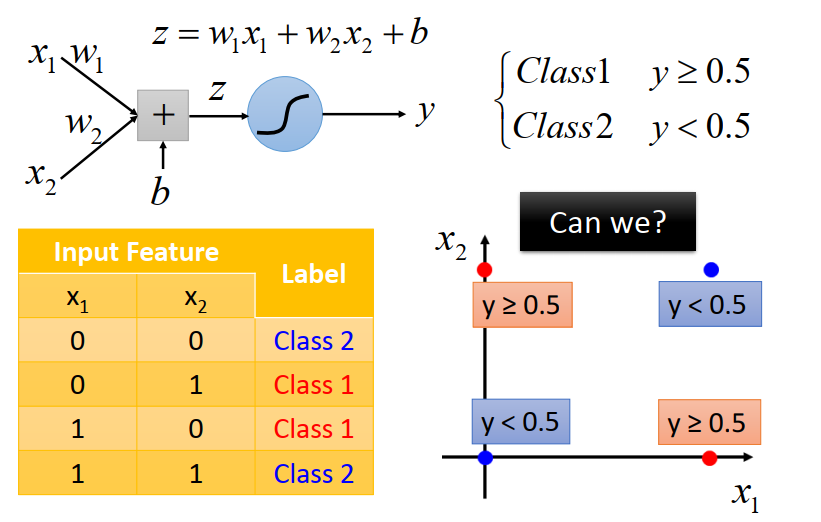
Logistic Regression 无法分割 class 1 和 class 2,因为Logistic Regression 分界线是一条直线,无论你怎么分,都无法分割开 class1 和 class 2。
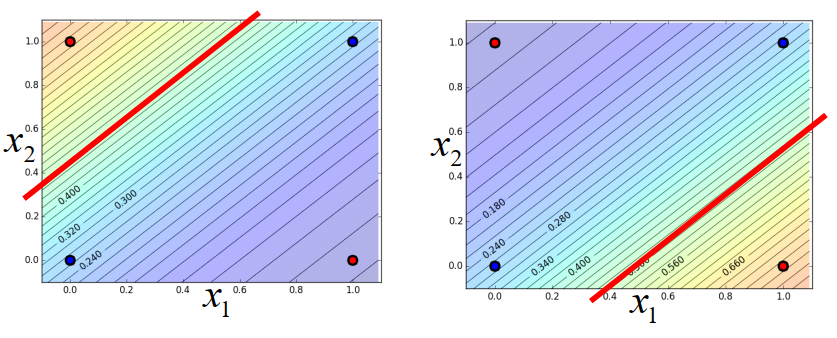
如果你坚持要用 Logistic Regression,那就需要做一下Feature Transformation
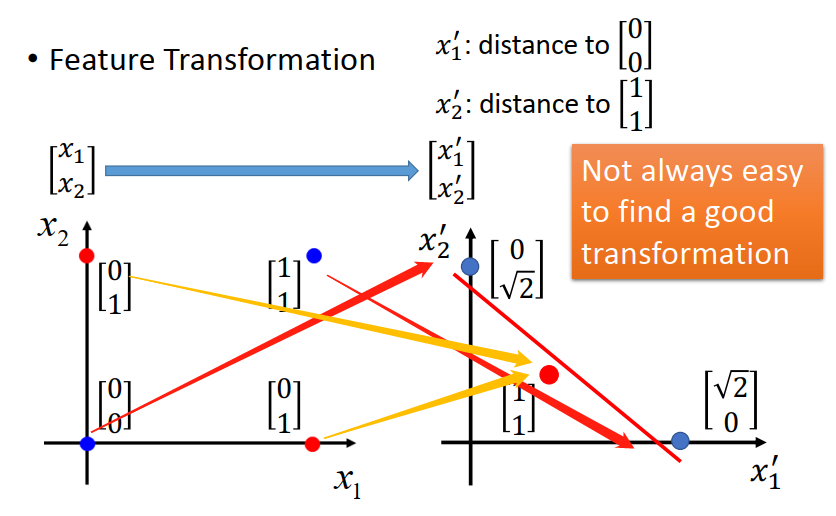
但是,麻烦的是我们不知道怎么做Feature Transformation。
为了做到这件事,我们需要Cascading logistic regression models (梦开始的地方)
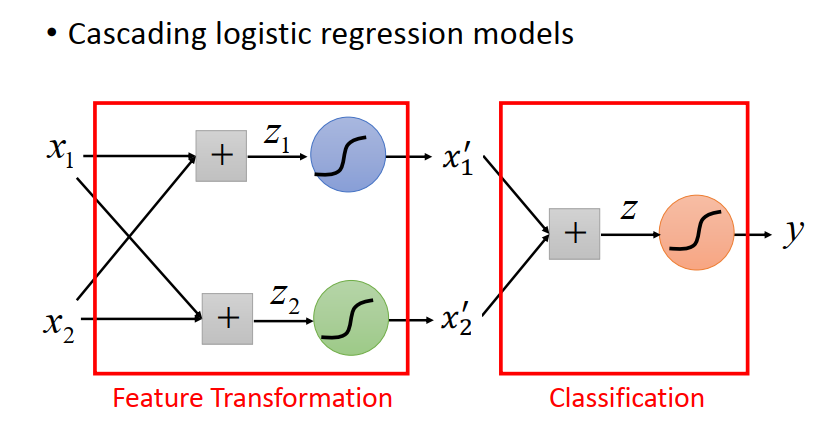
前面这两个Logistic Regression 做到就是 Feature Transformation 这件事件,后面这个Logistic Regression 来做分类。
实际例子如下:
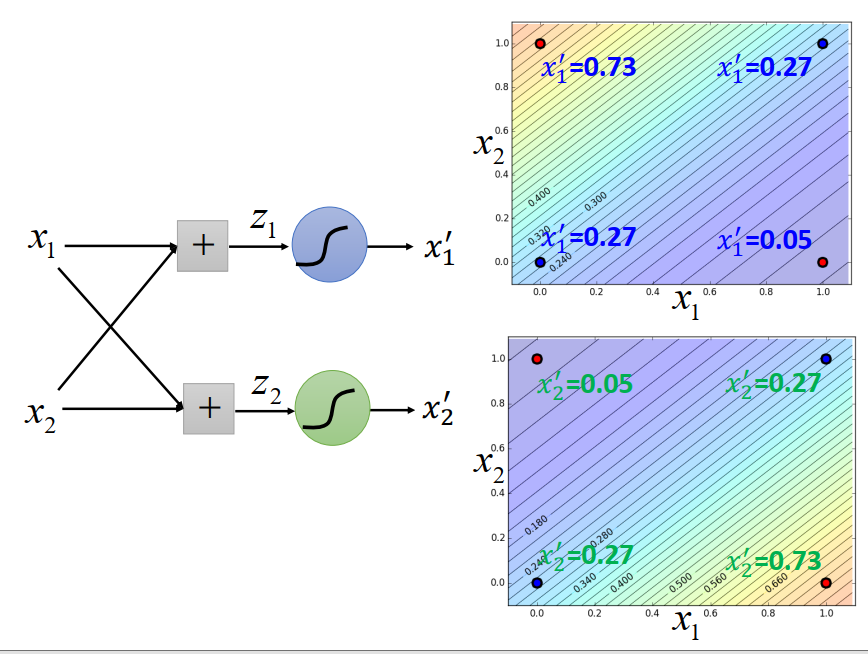
我们可以调整蓝色的Logistic Regression参数,让它的output 长成右上角这个样子(左上角output值比较大 ,右下角值比较小);
调整绿色的Logistic Regression参数,让它的output 长成右下角这个样子(左上低右下高)

有了前面这两个Logistic Regression以后,我们就可以做Feature Transformation 得到另一组Feature (上图右下角)
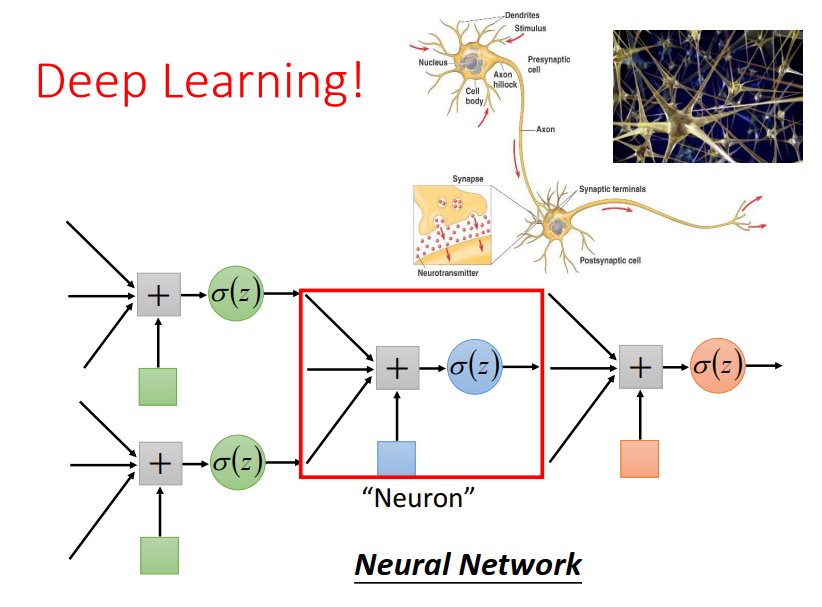
我们把每个Logistic Regression 叫做“Neuron” 这些Logistic Regression串起来所组成的网络叫做 Neural Network。这个东西就是Deep Learning。