[人工智能]2021-07-28学习笔记

记录一下jupyter的便捷操作

import pandas as pd
import numpy as np
#执行该代码可以使得当前nb支持多输出
from IPython.core.interactiveshell import InteractiveShell  
InteractiveShell.ast_node_interactivity = "all" 

#显示所有列
pd.set_option('display.max_columns', None)
#显示所有行
pd.set_option('display.max_rows', None)

#显示所有的array元素
np.set_printoptions(threshold=np.inf)
#其中，numpy对数组长度设置了一个阈值：
#1、数组长度<=阈值：完整打印；2、数组长度>阈值：以省略的形式打印；
#这里的np.inf只是为了保证这个阈值足够大，以至于所有长度的数组都能完整打印，可根据实际情况进行设置。
#比如，threshold=10000，那么数组长度<=10000的数组可以完整打印；数组长度>10000：以省略的形式打印。

集成学习案例一、居民幸福感调查建模from天池大数据竞赛

赛题背景：

此案例是一个数据挖掘类型的比赛——幸福感预测的baseline。比赛的数据使用的是官方的《中国综合社会调查（CGSS）》文件中的调查结果中的数据，其共包含有139个维度的特征，包括个体变量（性别、年龄、地域、职业、健康、婚姻与政治面貌等等）、家庭变量（父母、配偶、子女、家庭资本等等）、社会态度（公平、信用、公共服务）等特征。

赛题要求使用以上 139 维的特征，使用 8000 余组数据进行对于个人幸福感的预测（预测值为1，2，3，4，5，其中1代表幸福感最低，5代表幸福感最高）。 因为考虑到变量个数较多，部分变量间关系复杂，数据分为完整版和精简版两类。可从精简版入手熟悉赛题后，使用完整版挖掘更多信息。在这里我直接使用了完整版的数据。赛题也给出了index文件中包含每个变量对应的问卷题目，以及变量取值的含义；survey文件中为原版问卷，作为补充以方便理解问题背景。

最终的评价指标为均方误差MSE

文件：index.xlsx、submit_example.xls、train.xls、test.xls、survey.pdf

数据预处理

1、从excel中导入数据
2、对于数据中的连续出现的负数值进行处理，转换为有意义的数字【负数值没有实际意义，看index文件即知】
3、填充缺失值，使用fillna(value)方法，其中value的数值根据具体的情况来确定。例如将大部分缺失信息认为是零，将家庭成员数认为是1，将家庭收入这个特征认为是66365，即所有家庭的收入平均值。【主观判断，还可考虑众数或平均数】
4、与时间有关的信息，这里主要分为两部分进行处理：首先是将“连续”的年龄，进行分层处理，即划分年龄段，具体地在这里我们将年龄分为了6个区间。其次是计算具体的年龄。

总结：数据清洗一般思路：

• 缺失值插补
  • 均值、中位数、众数插补
  • 固定值插补，eg：0
  • 最近邻插补：前一个或后一个
• 离群值
  • 直接删除
  • 替换法
• 异常、冗余值
  • 直接删除

数据重采样

• 滑窗法：

1. 对于时间序列数据，选取不同的时间窗间隔，可以得到多份训练数据集
2. 该方法可以增加训练样本，也方便做交叉验证实验

• 非平衡重采样：调整正负样本量
  • 欠采样
  • 过采样
  • 组合采样

数据变换

• 连续变量离散化（分箱）

  • 等频
  • 等宽
  • 聚类

• 离散变量编码

  • One-hot Encoding
  • Label Encoding

• 长尾分布

  • Ln、Log

数据规范化

• Min-Max
• Z-score
• MaxAbs

特征工程：核心要义是去研究如何将样本表示出来，而特征工程解决的就是Representation的问题

1、数据增广（特征构造）

基于对原始数据的数据探索，不断构造新特征的过程定义为数据增广或特征构造。

基本方法：

• 理解字段
• 抽取实体
• 分析实体关系
• 设计特征群
• 按特征群分别构造特征
• 考察特征群关系，进一步构造新特征

经过思考，如下特征被加入：第一次结婚年龄、最近结婚年龄、是否再婚、配偶年龄、配偶年龄差、各种收入比（与配偶之间的收入比、十年后预期收入与现在收入之比等等）、收入与住房面积比（其中也包括10年后期望收入等等各种情况）、社会阶级（10年后的社会阶级、14年后的社会阶级等等）、悠闲指数、满意指数、信任指数等等。除此之外，我还考虑了对于同一省、市、县进行了归一化。例如同一省市内的收入的平均值等以及一个个体相对于同省、市、县其他人的各个指标的情况。同时也考虑了对于同龄人之间的相互比较，即在同龄人中的收入情况、健康情况等等

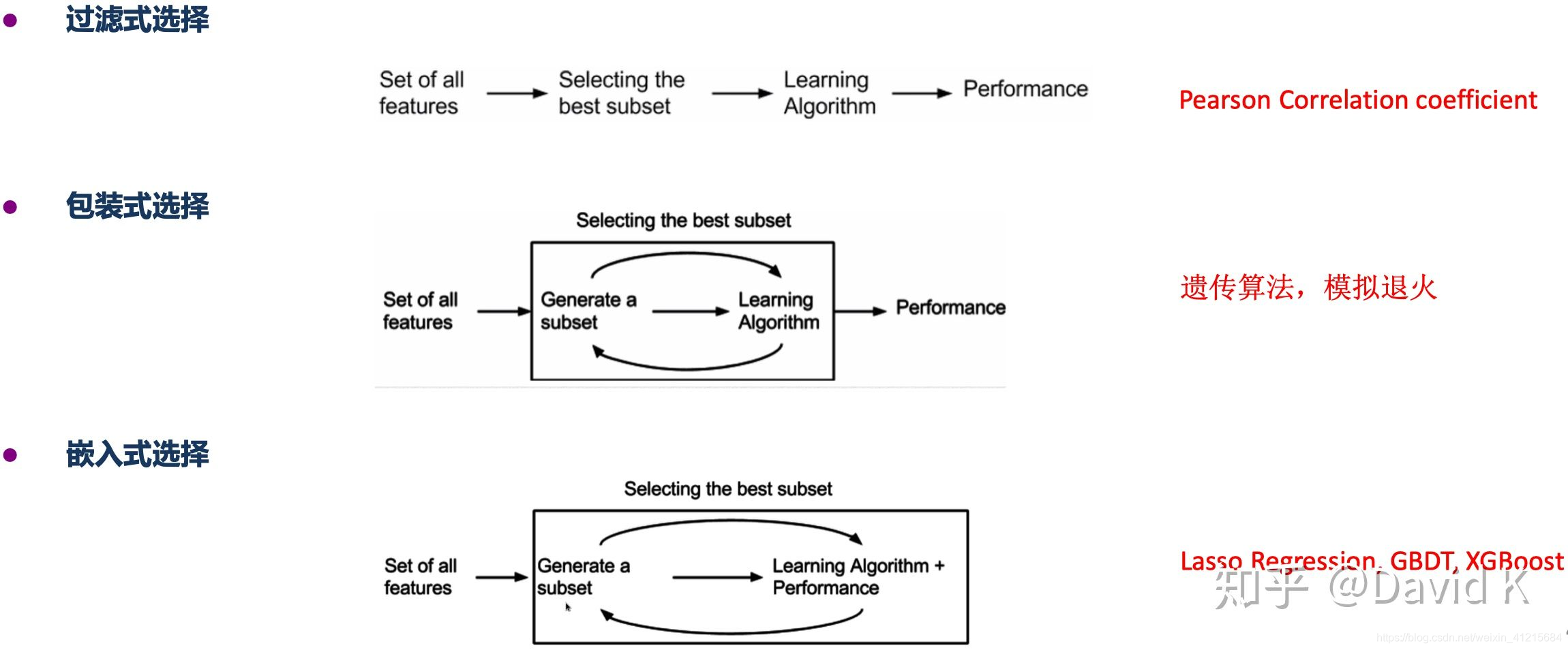
2、特征选择

常用的特征选择方法如下图所示，本文采用的是xgboost算法以选取最重要的49个特征（为什么不是50个？！因为第50个特征重要性突降很大，类似于主成分分析中主观选取主成分个数的思想）

特征建模（第一层的blending集成）

对于原始的263维的特征进行如下相同的操作
1.lightGBM
2.xgboost
3.RandomForestRegressor随机森林
4.GradientBoostingRegressor梯度提升决策树
5.ExtraTreesRegressor 极端随机森林回归
至此，我们得到了以上5种模型的预测结果以及模型架构及参数。其中在每一种特征工程中，进行5折的交叉验证，并重复两次Kernel Ridge Regression，取得每一个特征数下的模型的结果。

对于49维特征的操作
1.lightGBM
2.xgboost
3.GradientBoostingRegressor梯度提升决策树
至此，我们得到了以上3种模型的基于49个特征的预测结果以及模型架构及参数。其中在每一种特征工程中，进行5折的交叉验证，并重复两次Kernel Ridge Regression，取得每一个特征数下的模型的结果。

对于383维特征的操作
1.Kernel Ridge Regression 基于核的岭回归
2.使用普通岭回归
3.ElasticNet 弹性网络
4.BayesianRidge 贝叶斯岭回归
至此，我们得到了以上4种模型的基于383个特征的预测结果以及模型架构及参数。其中在每一种特征工程中，进行5折的交叉验证，并重复两次LinearRegression，取得每一个特征数下的模型的结果

对于49维数据，考虑更多的模型
1.Kernel Ridge Regression 基于核的岭回归
2.使用普通岭回归
3.ElasticNet 弹性网络
4.BayesianRidge 贝叶斯岭回归
至此，我们得到了以上4种模型的基于383个特征的预测结果以及模型架构及参数。其中在每一种特征工程中，进行5折的交叉验证，并重复两次LinearRegression，取得每一个特征数下的模型的结果

模型融合（第二层的blending集成）

将以上的4中集成学习模型再次进行集成学习的训练，这里直接使用LinearRegression简单线性回归的进行集成。

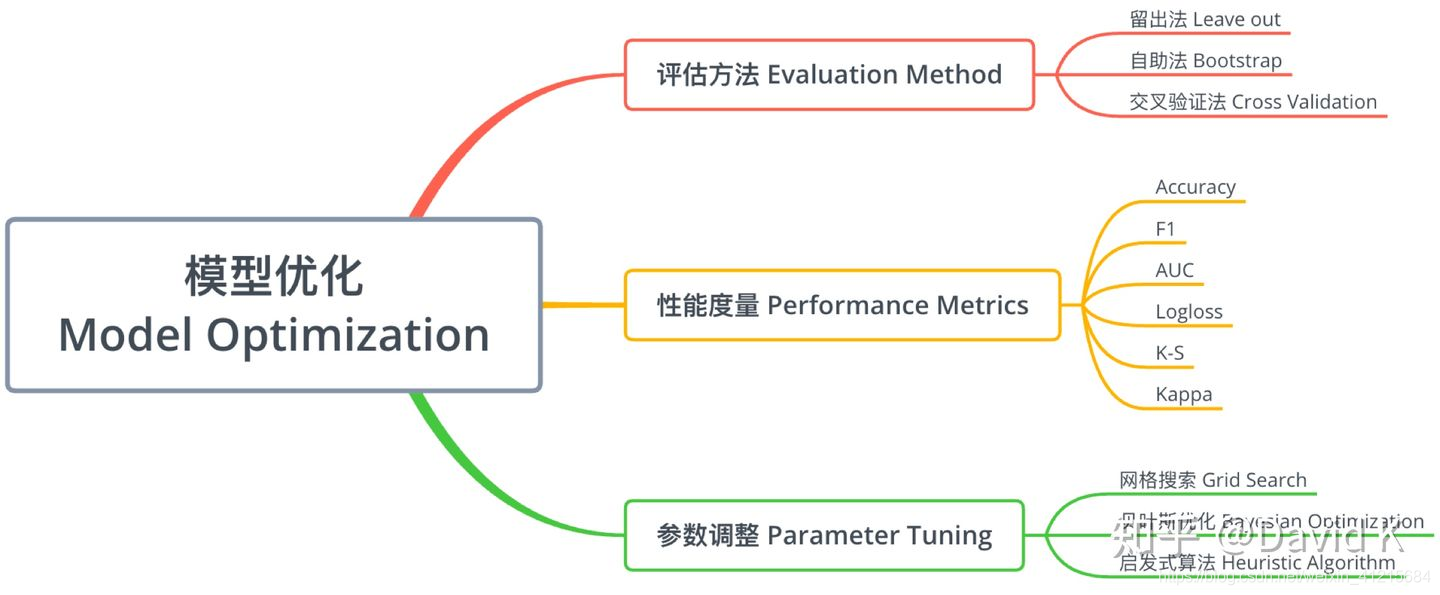
模型优化