学习内容
这是第二次看机器学习的内容,所以这里主要记录的是让我印象深刻的知识点;
但是有两个问题:
- deep? 为什么不是越深越好?
- fat? 为什么要套娃,我们只需要将多个sigmoid并排不就好了吗? 因为我需要的就是y = constant + sum(蓝线)
深度学习的类别
输入可以是当前的特征; 各种条件;
- 回归: 函数输出一个标量;
- 分类:给出一堆类别,函数需要根据某个物体的所有特征输出它属于的一个标签;
比如垃圾邮件; 阿尔法go - Structured learning: 学会创造某些东西(image、document)
1. Function with Unknown Parameters
后面我们会以这个例子作为示例;
比如某个频道的Youtube流量; 而该流量是由前面所有的流量决定的;
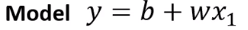
Function = Model
feature = 表示我们已经知道的东西(在这里指的是前面有的每天的观看人数);
weight = w
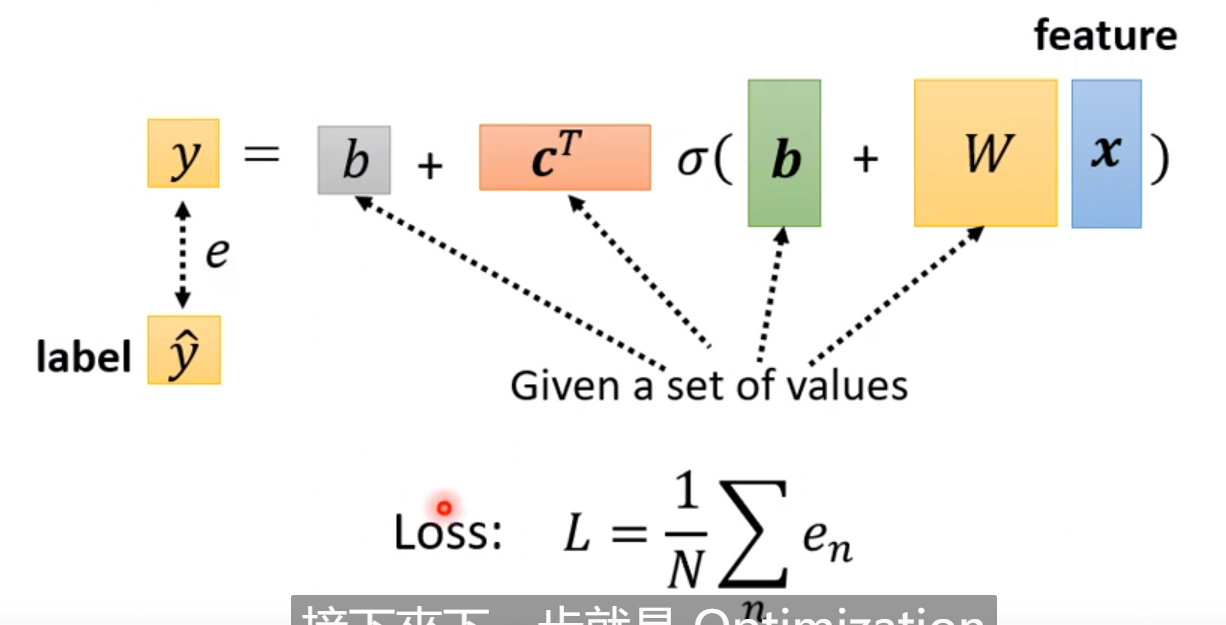
2. Define Loss from Training Data
就是我们给出参数后,查看这些参数的效果是不是好!
也就是看真实值和估值的差距;
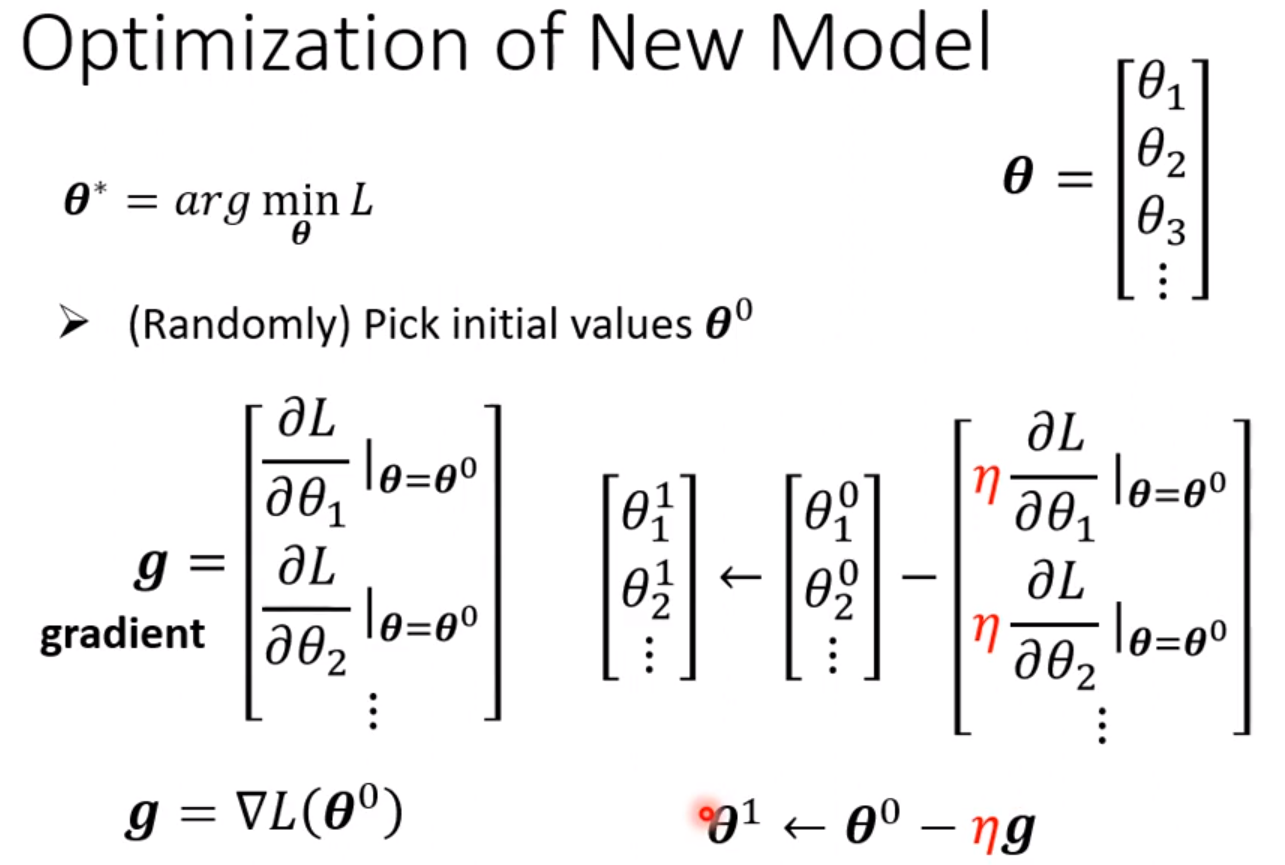
3.Optimization
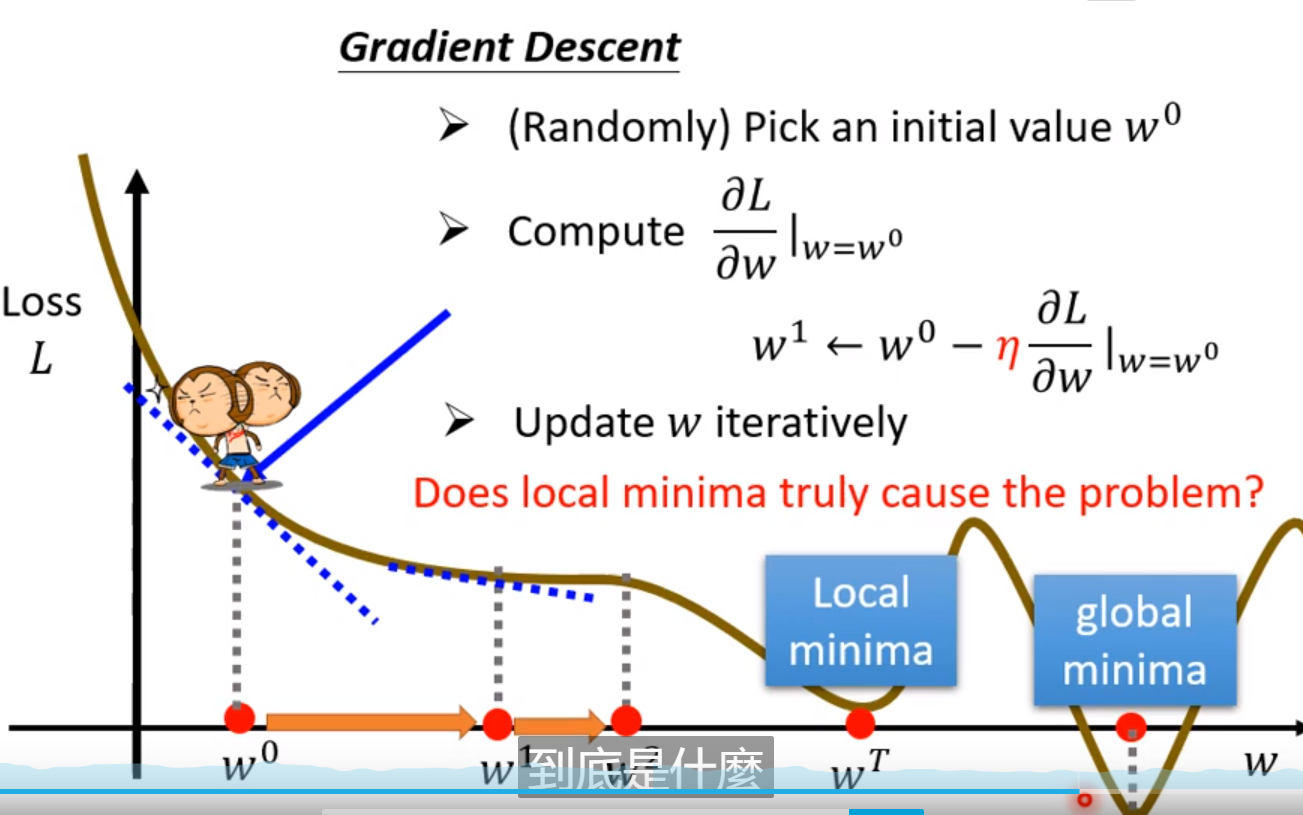
问题1: 为什么学习率在训练的时候要调整?
- 因为刚开始时一般远离最优点,所以刚开始的时候我们要选择较大的学习率,后面再调整学习率,所以会有随着epoch值改变的动态学习率;
问题2:为什么loss有些时候是负的?
- 因为你斜率一定的时候,跨度大了,必然会有负的;
问题3: 学习率是啥?
就是梯度前面的东西;
问题4: 两个参数怎么更新呢?


问题5: sigmoid为什么是三个?
一般而言,sigmoid的个数越多,那么效果就会越好;
一个sigmoid表示的就是一个蓝色折线,那么多个sigmoid就会使得无限接近于原来的数值(beyond precise function),也就会出现过拟合!
问题6:为什么是sigmoid,不能是hard sigmoid?
当然可以,只要你能写出来!
问题7:hyperparameter有哪些?
学习率(步长么)、几个sigmoid、batchsize也是;
改进函数第一次(线性化)
函数的改进都源于你对这个问题的理解;
比如我们要预测观看学习视频的人数,我们可以把它想想为一个线性回归问题,类似于y = b + kx;
其中x表示前一天的观看人数,而y表示的隔天的观看人数,b是偏差(这里x不是天数,星期一、星期二等);
但是呢,某一天的观看人数不能仅仅是通过前一天来决定,每一天的权重应该是不一样的,周一到周五权重应该会更大,而周六和周天权重会降低,所以我们做出第一次改进,ki,i=1…7;但是我们可能认为7不够,应该是一个月,那么i = 1…31;
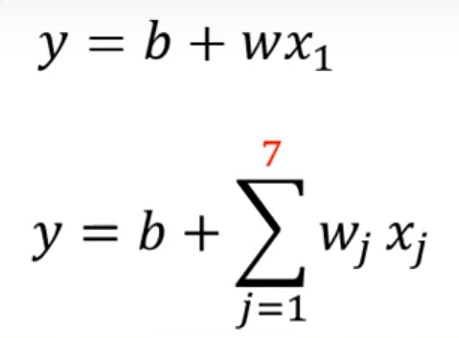

3. sigmoid的由来与应用
sigmoid就是一个可以表示各个函数的框架!
3.1 sigmoid的由来

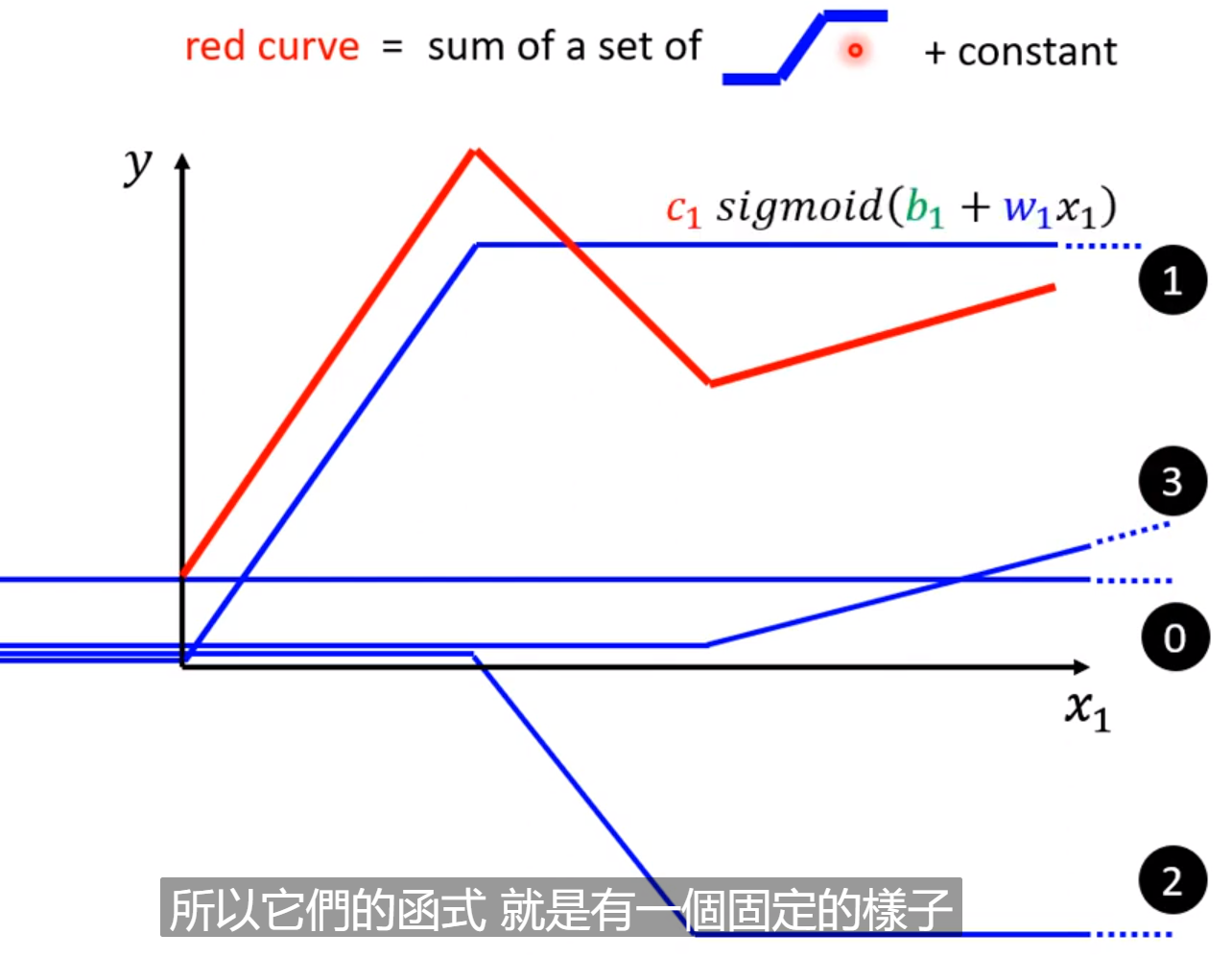
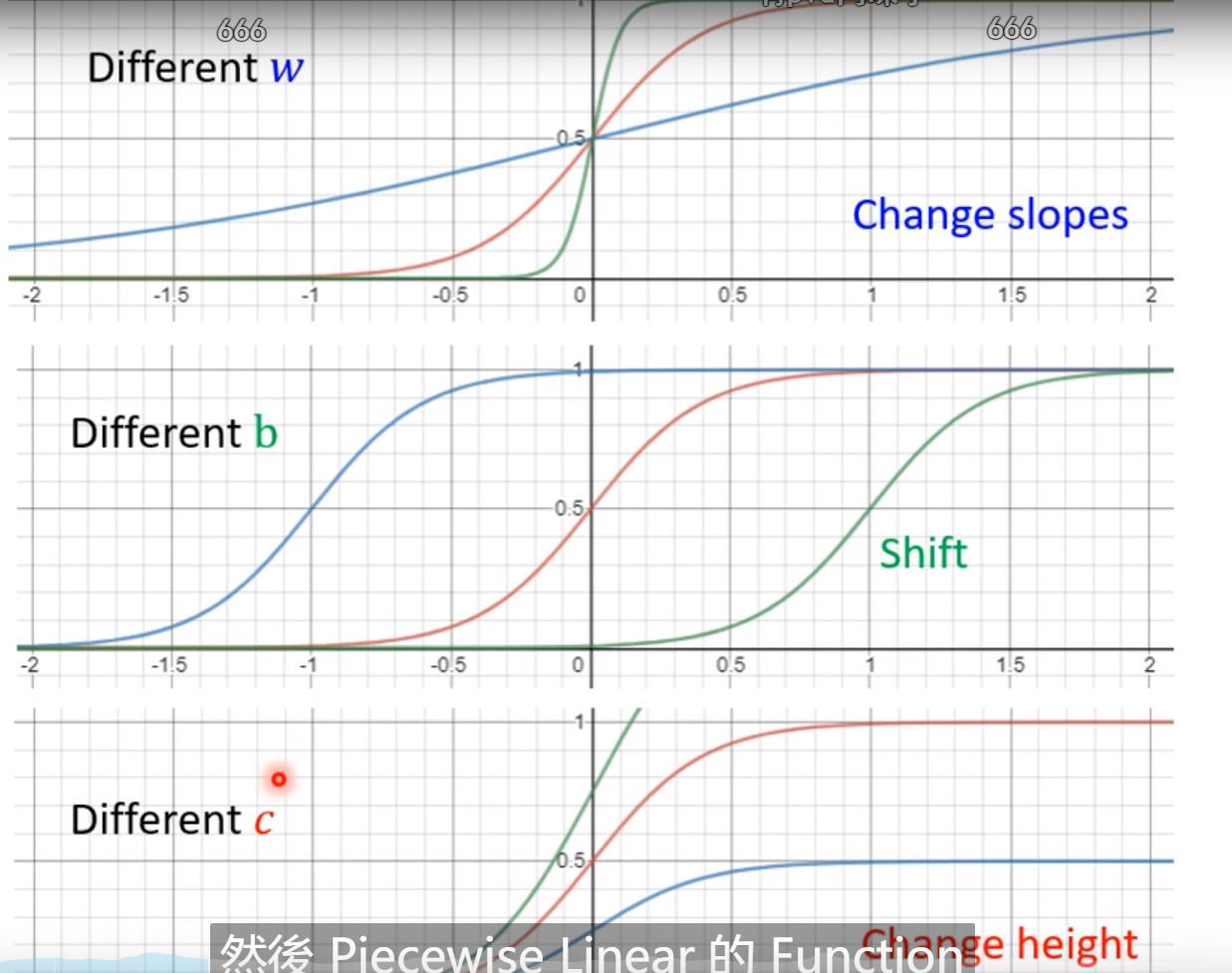
我们通过c、b和w来定义出这个曲线,从而模拟蓝色的function;
我们可以将e取消,那么就是
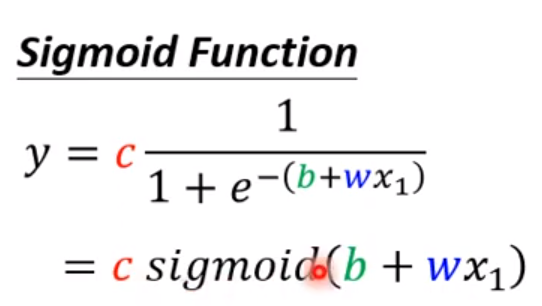
3.2 sigmoid的应用
前面已经知道了sigmoid可以代表各个直线或者是曲线,只需要改变中间的w和b即可,所以我们怎么表示我们的模型呢? 那么就是将上面的〇 + ①、②和③用sigmoid来替代;

改进函数第二次(神经网络)

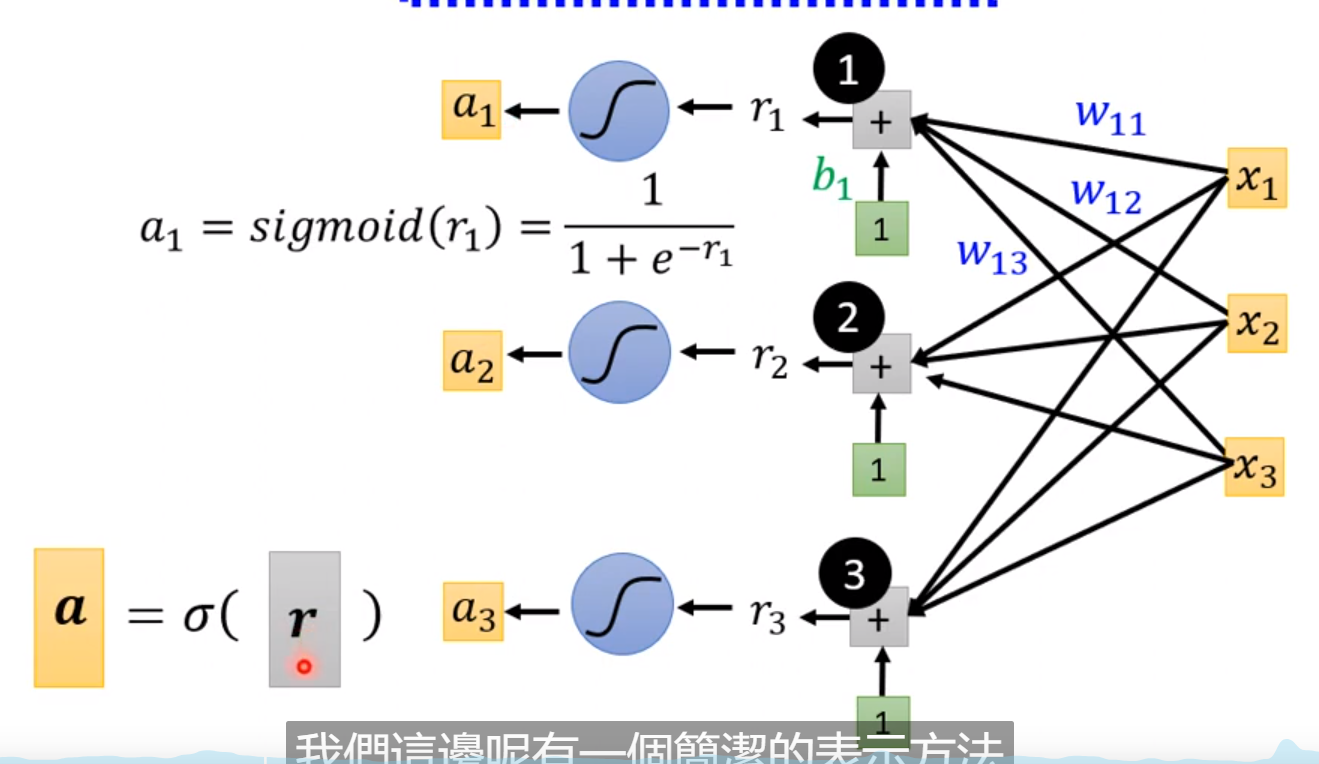
由于我们上面已经得到了多个特征表示,每天一个特征表示(也就是观看的人数),所以放入sigmoid中,那么就会得到上图下面的式子;
特别注意的是,这里的
W
i
j
W_{ij}
Wij?是wi和wj的结合体,内外参数也就是其实是两个参数,所以才会有Wij。
全连接网络BP
这里我们去j: 1,2,3; i:1,2,3; 也就是取前三天、并且设立三个sigmoid(三个函数);
这里的
W
1
j
W_{1j}
W1j?表示的是第一个sigmoid函数里面的三个特征值的权重值;
计算r向量


计算a向量
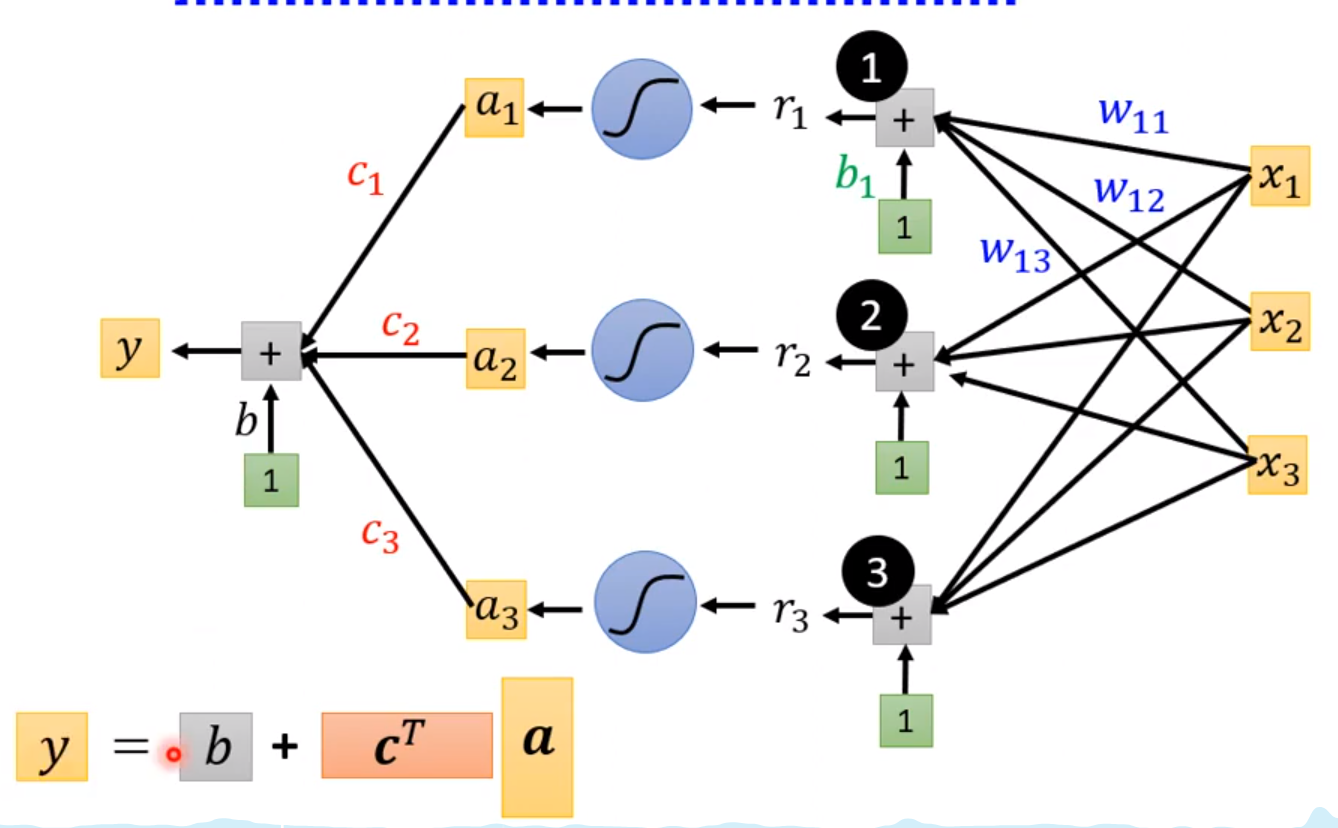
y = constant + sum(蓝线)
参数更新
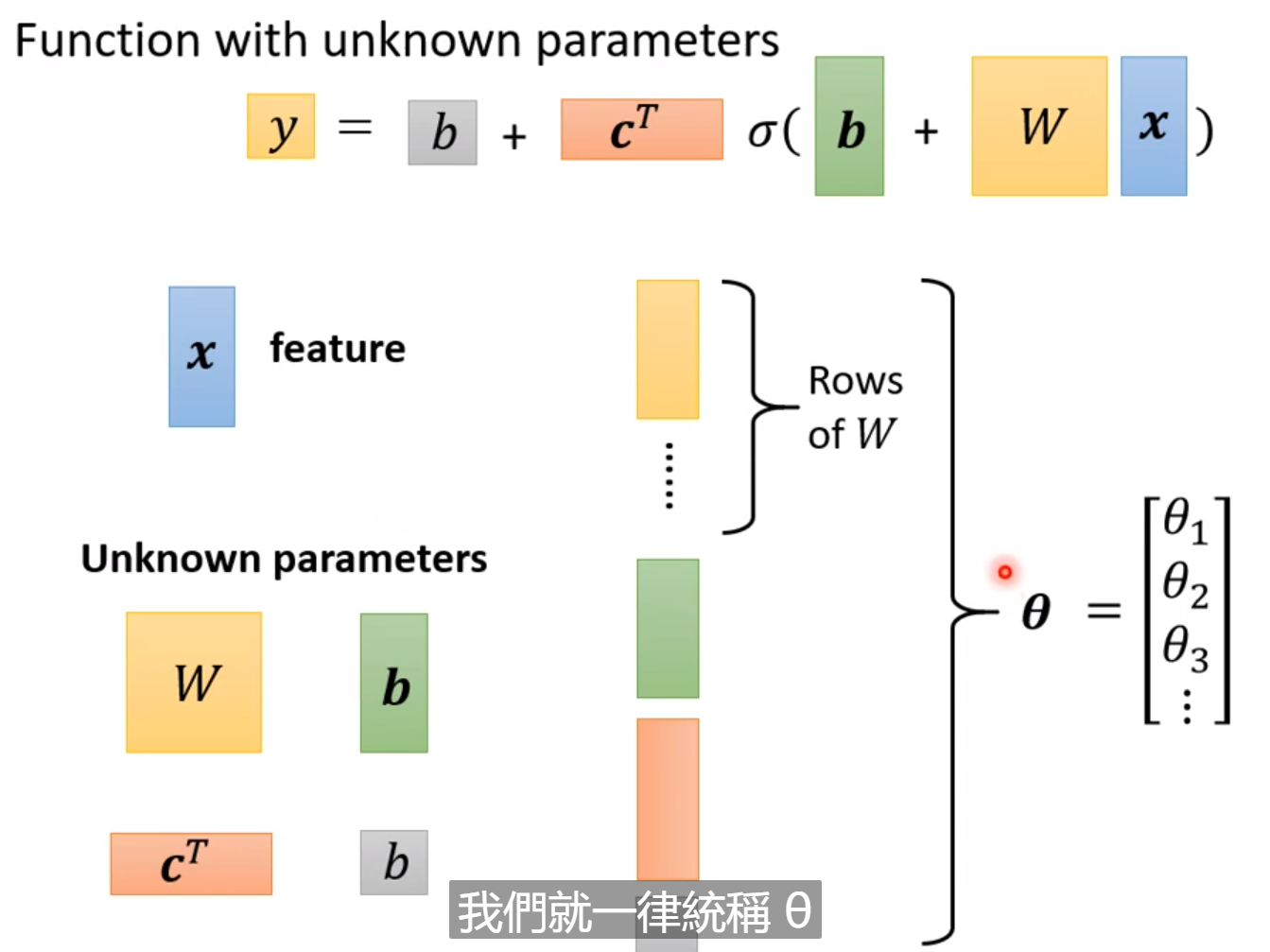
参数: 注意这里两个b是不一样的,里面的b是一个向量,外面的b是一个值;
我们将所有的参数都列出来concat为一个向量
θ
\theta
θ
Loss: 就是预测值和gt的误差;
优化器: 和前面的一样,都是学习率 * 梯度来更新参数;
参数的初始化是不一样的! 我们初始化得到
θ
0
\theta^{0}
θ0,而下标表示的是第几个参数。
其中倒三角的意思是梯度向量。
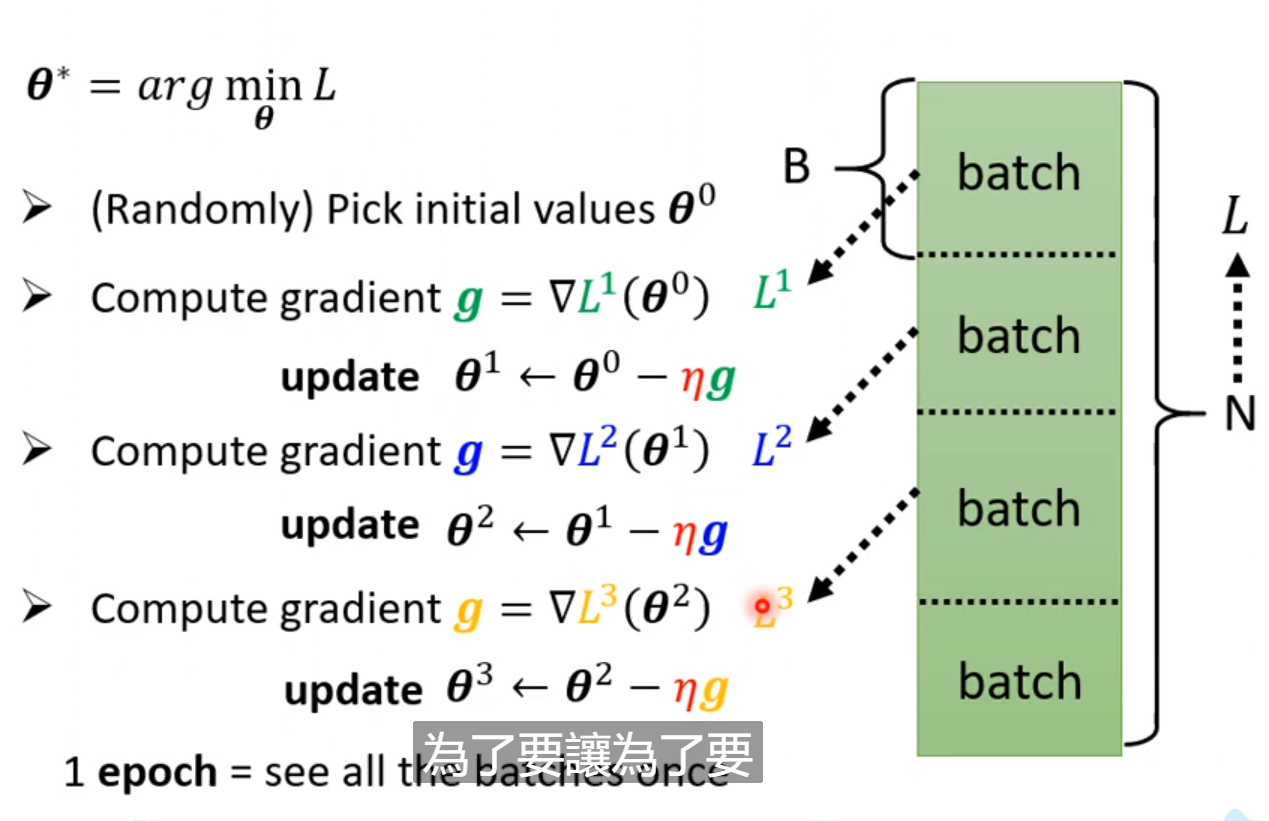
4. Update(SGD(小批量梯度下降))
Update 和 Epoch是不一样的!
原数据库为N, 每个Batch有batch_size的大小,我们的参数的Update是在经历每次batch后进行更新的。而所有的batch都进行了一次了就可以称为是一个epoch,所以在一个epoch中有多次Update,共N/batch_size次参数更新;
激活函数
激活函数 = 函数框架
它可以有很多种替代,其中sigmoid只是其中之一; 比如下面的ReLU;
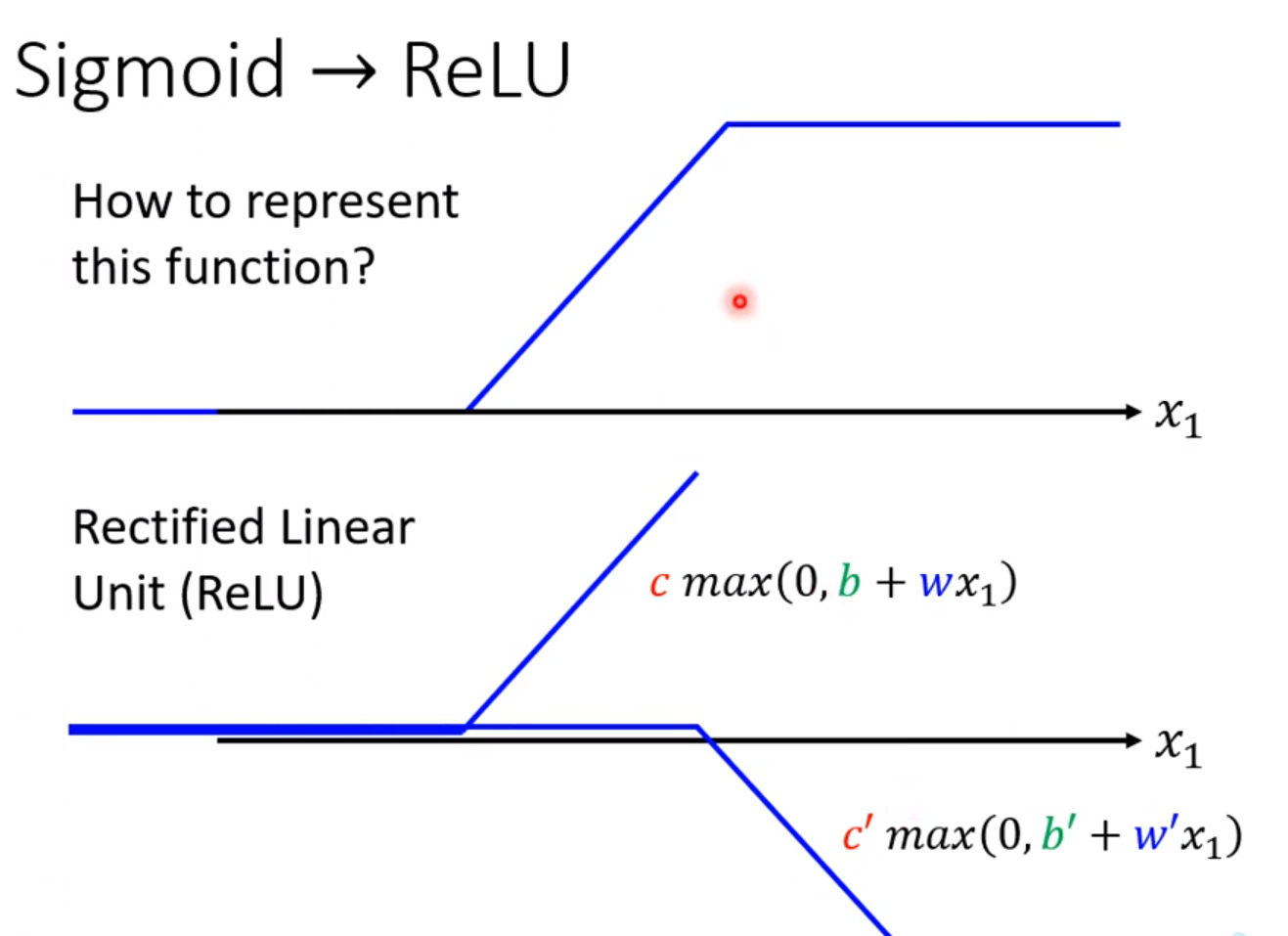
ReLU: 如果 0 > (b + wx1)那么,就输出0;
两个ReLU相加就是一个hard sigmoid!
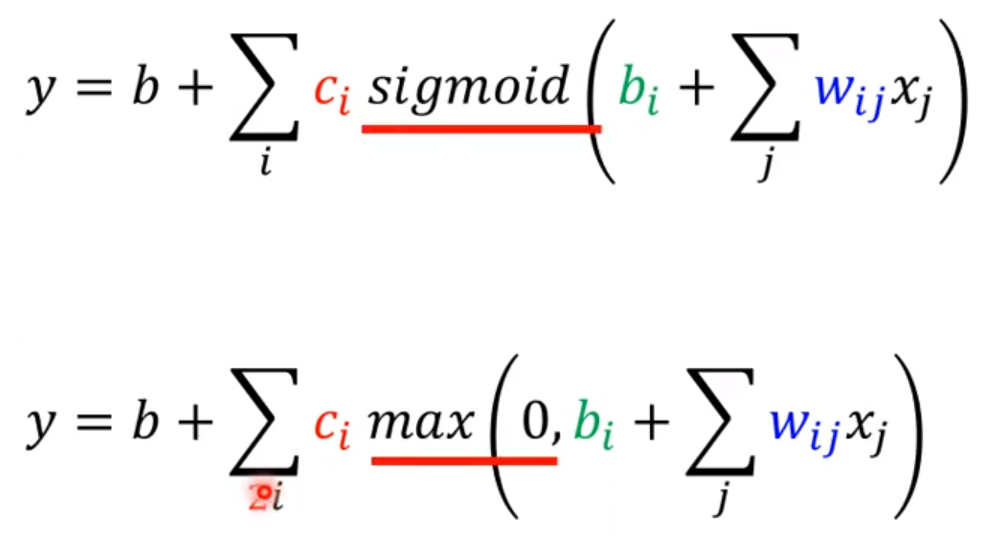
改进模型第三次(多个激活函数)
一般而言,sigmoid的个数越多,那么效果就会越好;
一个sigmoid表示的就是一个蓝色折线,那么多个sigmoid就会使得无限接近于原来的数值(beyond precise function),也就会出现过拟合!
改进模型第四次(多个layer)套娃


如上图所示,我们将上一个激活函数后的a当作特征再次放入到下一个激活函数(增加了新的参数),那么就叫做加layer
深度学习(deep = hidden layer)
激活函数就是neural network! 但是我们将它命名为layer! deep = hidden layer,就是深度学习!
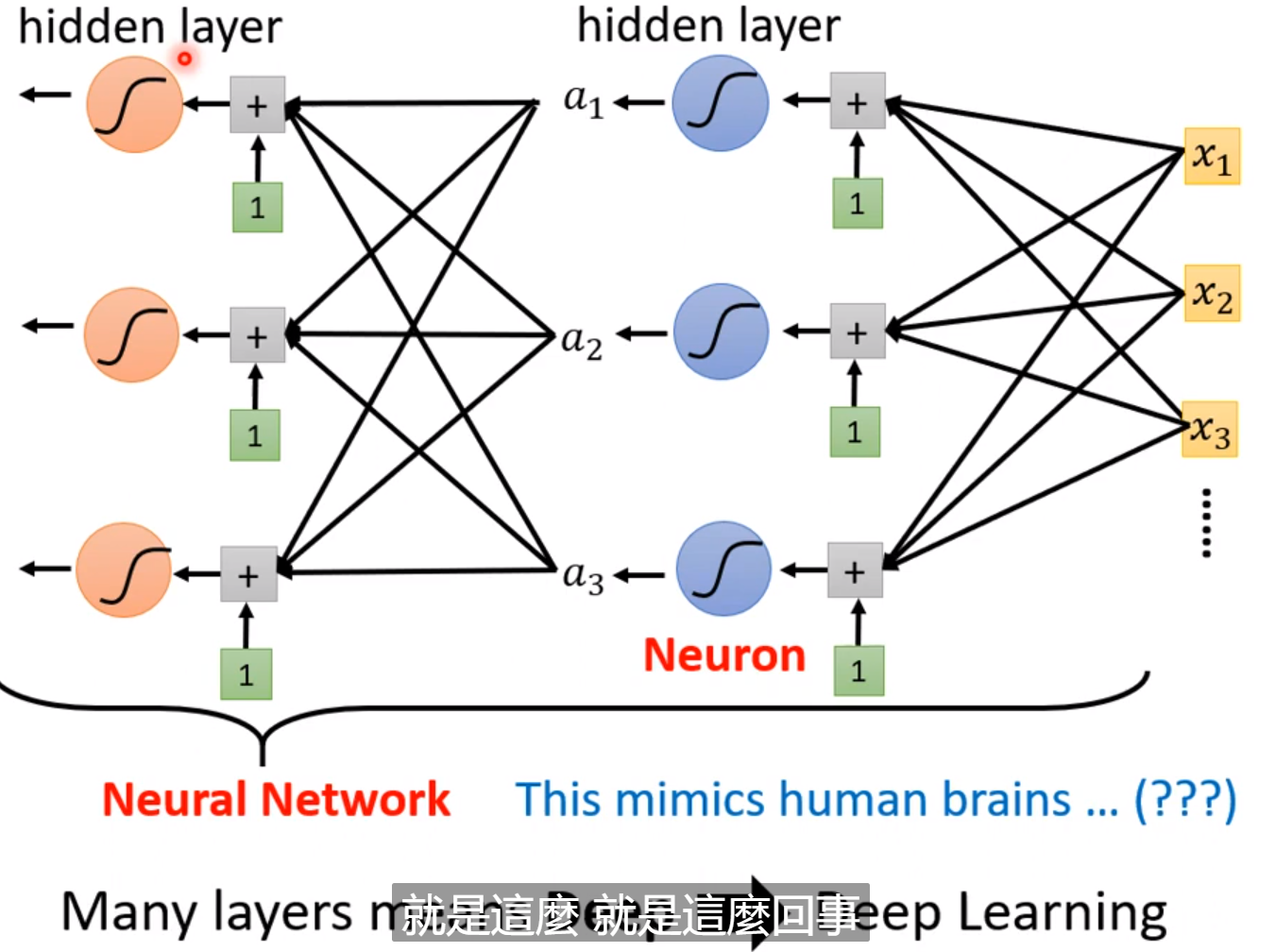
所以才会有层数越来越多!网络也越来越深! AlexNet、GoogleNet、Residual Network、Taipei等等;
但是深度不是越深越好,不仅会出现过拟合,也会出现效果越来越差的情况。
但是有两个问题:
为什么不是越深越好?
为什么要套娃,我们只需要将多个sigmoid并排不就好了吗?
overfitting
在训练集上更好,但是在测试集上效果反而差了,这就叫做过拟合!
