写在前面
我终于把神经网络的梯度下降公式推导完毕了!先看看为了伟大工程牺牲的草稿纸吧~

接下来我就分享出我推导的公式以及我总结出来的规律。
正文
主要内容在我的古月居博客:
[BPnet识别MNIST05]神经网络梯度下降公式分析
梯度下降
神经网络如图所示:
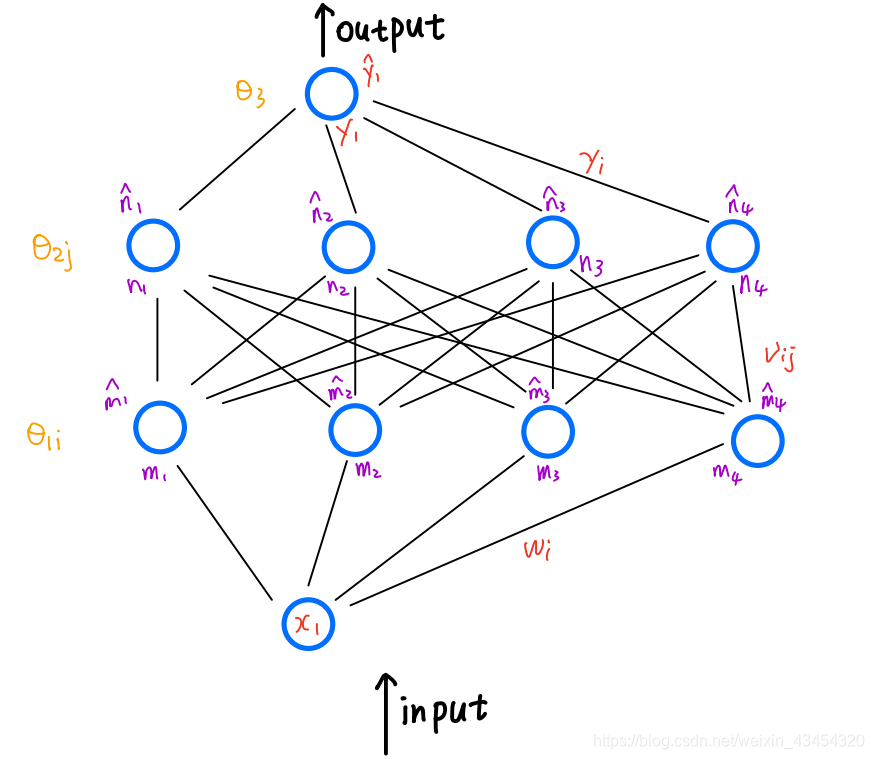
公式分析
各个神经元的输入输出关系我已经在上一篇博客中给出了,这里再集中给出一下:
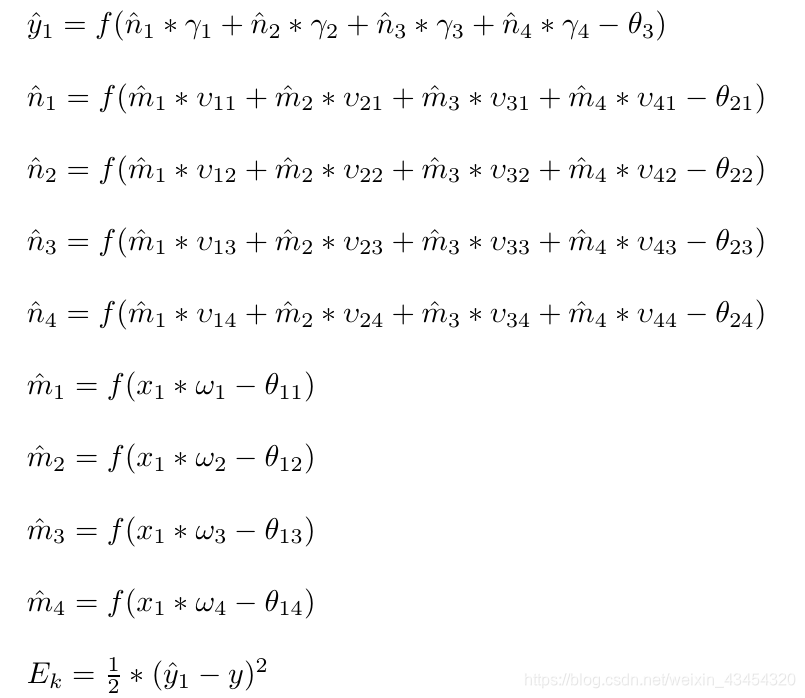


latex源码:
\\
$
\frac{\partial E_{k}}{\partial \nu{ij}} = (\hat{y}_{1} - y)*[\hat{y}_{1}*(1-\hat{y}_{1})]*
[\hat{n}_{j}*(1-\hat{n}_{j})]*\gamma_{j}*\hat{m}_{i}
$
\\
\\
$
\frac{\partial E_{k}}{\partial \gamma{i}} = (\hat{y}_{1} - y)*[\hat{y}_{1}*(1-\hat{y}_{1})]*\hat{n}_{i}
$
\\
\\
$
\frac{\partial E_{k}}{\partial \omega{i}} = \sum_{i=1}^{4} (\hat{y}_{1} - y)*[\hat{y}_{1} * (1-\hat{y}_{1})] *[\hat{n}_{i}*(1-\hat{n}_{i})]*\gamma_{i} * [\hat{m}_{i}*(1-\hat{m}_{i})] * \nu_{ii} * x_{1}
$
\\
\\
$
\frac{\partial E_{k}}{\partial \theta{1i}} = \sum_{j=1}^{4} (-1) * (\hat{y}_{1} - y)*[\hat{y}_{1} * (1-\hat{y}_{1})] *[\hat{n}_{j}*(1-\hat{n}_{j})]*\gamma_{j} * [\hat{m}_{i}*(1-\hat{m}_{i})] * \nu_{ij}
$
\\
\\
$
\frac{\partial E_{k}}{\partial \theta{2i}} = (-1)*(\hat{y}_{1} - y)*[\hat{y}_{1}*(1-\hat{y}_{1})]*
[\hat{n}_{i}*(1-\hat{n}_{i})]*\gamma_{i}
$
\\
\\
$
\frac{\partial E_{k}}{\partial \theta{3}} = (-1) * (\hat{y}_{1} - y)*[\hat{y}_{1}*(1-\hat{y}_{1})]
$
\\
正文
主要内容在我的古月居博客:
[BPnet识别MNIST05]神经网络梯度下降公式分析

