目录
第六章 支持向量机
6.1 间隔与支持向量
分类学习的基本思想就是基于训练集在样本空间中找到一个划分的超平面,将不同类别的样本分开。那么,什么样的划分是最优的呢?直观来看,找位于两类训练样本的“正中间”是最好的划分面因为这样的划分对局部扰动的容忍性最高。那么我们应该如何量化度量这个最好划分面呢?

在样本空间中,划分超平面可通过如下线性方程来描述:
?
其中{
}为法向量,b为位移项,决定了超平面与原点之间的距离。则样本空间中任意点x到超平面(ω,b)的距离可写为
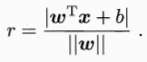
假设超平面(ω,b)能将训练样本正确分类,即对于(xi,yi)∈D,令
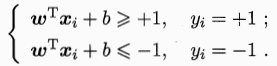
如图,距离超平面最近的这几个训练样本点使上式的等号成立,它们被称为支持向量?(support vector),两个异类支持向量到超平面的距离之和为
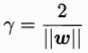
?它被称为间隔(margin)
支持向量机(Support Vector Machine,简称SVM)的基本型为了找到具有最大间隔(maximum margin)的划分超平面,也就是让γ最大,即?
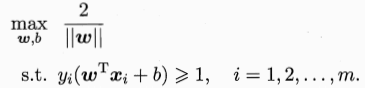
也即
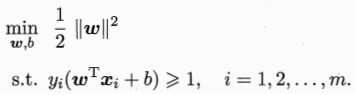
6.2 对偶问题
任何一个求极大化的线性规划问题都有一个求极小化的线性规划问题与之对应,反之亦然,如果我们把其中一个叫原问题,则另一个就叫做它的对偶问题,并称这一对互相联系的两个问题为一对对偶问题。支持向量机的基本型使用拉格朗日乘子法可得到它的对偶问题:

6.3 核函数
由于在现实任务中,原始样本空间内可能并不存在一个能正确划分两类样本的超平面。对于这些问题,可将样本从原始空间映射到一个更高维度的特征空间,使其线性可分。??

令?(x)表示x映射后的特征向量,在特征空间中划分超平面所对应的模型可表示为:?
![]()
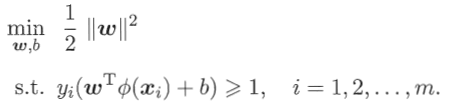
对偶问题为

求解可以得到

这里的κ(.,.)就是核函数。上式显示出模型最优解可通过训练样本的核函数展开,这一展开式亦称支持向量展式?
6.4 软间隔与正则化
现实中很难确定合适的核函数。使得训练样本在特征空间中线性可分,即使貌似线性可分,也很难断定是否是因过拟合造成的(硬间隔)所以引入软间隔(允许在一些样本上不满足约束)

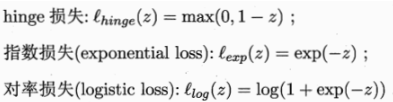
?

?正则化
无论用什么替代损失函数,这些学习模型都具有一个共性:优化目标中的第一项用来描述划分超平面的“间隔”大小,另一项∑mi=1l(f(xi),yi)用来表述训练集上的误差,可写为更一般的形式:?
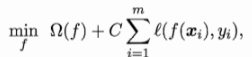

6.5 支持向量回归

参考

