[人工智能]降维与特征选择

内容简介

• 主成分分析
• 主成分分析建模
• 偏最小二乘法
• 偏最小二乘法建模
• Fisher LDA
• 特征选择方法

主成分分析（Principle Component Analysis, PCA）

• 主成分分析是一种线性、非监督、全局的降维算法

• PCA的目的是找到数据中的主成分，并利用这些主成分表征原始数据从而达到降维的目的

  具体讲就是：用少数的若干新变量（原变量的线性组合）替代原变量，新变量要尽可能多地反映原变量的数据信息，同时，新变量之间相互正交，可以消除原变量中相互重叠的信息

主成分分析过程推导

设样本的标准化输入变量矩阵为：

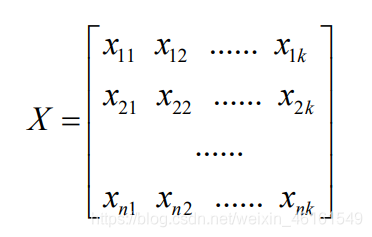
构造一个变量$P_1$，且变量$P_1$能携带标准化输入变量矩阵$X_{n?k}$的信息，满足以下公式：

在信号处理领域，认为信号具有较大的方差，噪声具有较小的方差，信号与噪声之比称为信噪比。信噪比越大意味着数据质量越好，反之，信噪比越小；
如下图，黄线所处的轴数据分布更为分散，数据在这个方向上方差更大；显然，黄线就是主成分所在的轴

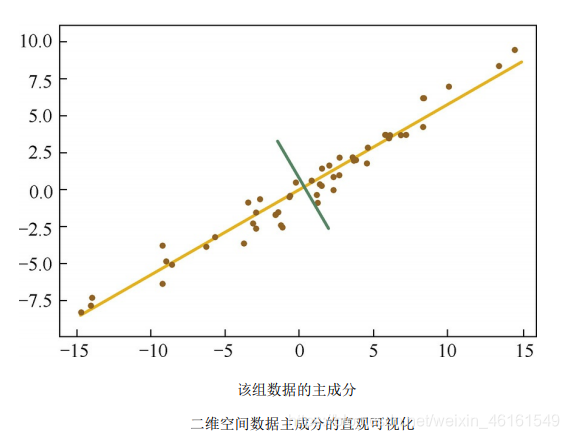
从概率统计观点可知，变量的方差越大，该变量包含的信息越多；因此，上述问题可以转化为要求变量$P_1$的方差最大。 $P_1$的方差为

构造拉格朗日函数：

其中，${\lambda }_1$为拉格朗日系数，分别计算$L$对${\lambda }_1$和${\mathbf{t}}_1$的偏导数，并令其为零，则有：

由上式知，${\mathbf{t}}_1$是$V$的一个标准化特征向量，${\lambda }_1$为其对应的特征值，故：

显然，${\mathbf{t}}_1$是矩阵$V$的最大特征值${\lambda }_1$所对应的标准化特征向量，对应的构造变量$P_1=X{\mathbf{t}}_1$称为第一主成分，且第一主成分包含的特征信息最多；同理可以求出$X$的第$m$个主成分$P_m=X{\mathbf{t}}_1$，且第$m$个主成分包含的特征信息少于第$m?1$个主成分特征信息，第$m+1$个主成分包含的特征信息远远小于第一主成分包含的特征信息；

前$m$个主成分携带的信息综合为：

主成分分析建模

%% I. 清空环境变量
clear all
clc

%% II. 导入数据
load spectra;

%% III. 随机划分训练集与测试集
temp = randperm(size(NIR, 1));
% temp = 1:60;
%%
% 1. 训练集——50个样本
P_train = NIR(temp(1:50),:);
T_train = octane(temp(1:50),:);
%%
% 2. 测试集——10个样本
P_test = NIR(temp(51:end),:);
T_test = octane(temp(51:end),:);

%% IV. 主成分分析
%%
% 1. 主成分贡献率分析
[PCALoadings,PCAScores,PCAVar] = pca(NIR);
figure
percent_explained = 100 * PCAVar / sum(PCAVar);
pareto(percent_explained)
xlabel('主成分')
ylabel('贡献率(%)')
title('主成分贡献率')

%%
% 2. 第一主成分vs.第二主成分
[PCALoadings,PCAScores,PCAVar] = pca(P_train);
figure
plot(PCAScores(:,1),PCAScores(:,2),'r+')
hold on
[PCALoadings_test,PCAScores_test,PCAVar_test] = pca(P_test);
plot(PCAScores_test(:,1),PCAScores_test(:,2),'o')
xlabel('1st Principal Component')
ylabel('2nd Principal Component')
legend('Training Set','Testing Set','location','best')

%% V. 主成分回归模型
%%
% 1. 创建模型
k = 4;
betaPCR = regress(T_train-mean(T_train),PCAScores(:,1:k));
betaPCR = PCALoadings(:,1:k) * betaPCR;
betaPCR = [mean(T_train)-mean(P_train) * betaPCR;betaPCR];
%%
% 2. 预测拟合
N = size(P_test,1);
T_sim = [ones(N,1) P_test] * betaPCR;

%% VI. 结果分析与绘图
%%
% 1. 相对误差error
error = abs(T_sim - T_test) ./ T_test;
%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 
%%
% 3. 结果对比
result = [T_test T_sim error]

%% 
% 4. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值','location','best')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)

偏最小二乘法（Partial Least Squares, PLS）

• 线性判别分析(Linear Discriminant Analysis，LDA)是一种有监督学习算法，经常被用来对数据进行降维，偏最小二乘法是其中一种分类器准测。

• PLS的核心思想是逐步回归，逐步分解输入变量矩阵和输出变量矩阵，并综合考虑提取的主成分对输入变量矩阵和输出变量矩阵的解释能力，直到满足性能要求为止

  PCA方法提取出的前若干个主成分携带了原输入变量矩阵的大部分信息，消除了相互重叠部分的信息。并没有考虑主成分对输出变量的解释能力嘛，方差贡献率很小但对输出变量有很强解释能力的主成分将会被忽略掉，这无疑会对校正模型的性能产生一定的影响。偏最小二乘法（PLS）可以很好地解决这个问题。

PLS公式推导

设标准化的输入变量矩阵和输出变量矩阵分别为：

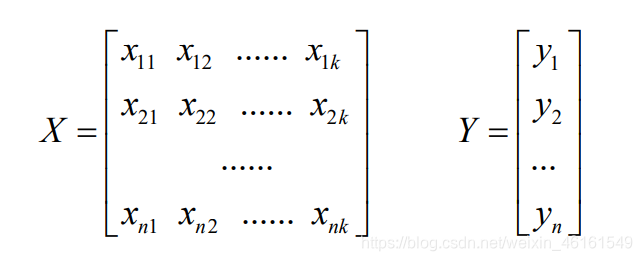
要求构造变量${\mathbf{t}}_1$和${\mathbf{u}}_1$满足：

且，变量${\mathbf{t}}_1$和${\mathbf{u}}_1$满足以下三个条件：

• ① 应尽可能大地携带输入变量矩阵 的信息；
• ② 应尽可能大地携带输出变量矩阵 的信息；
• ③ 和 应具有尽可能大的相关程度；

由主成分分析原理可知，条件①和条件②等价于要求${\mathbf{t}}_1$和${\mathbf{u}}_1$的方差尽可能地大，即

根据典型相关分析，条件③可以转换为使得${\mathbf{t}}_1$和${\mathbf{u}}_1$的相关系数尽可能地大，即

上述问题可以转化为计算${\mathbf{t}}_1$和${\mathbf{u}}_1$的协方差的最大值，即

构造拉格朗日函数并求解：


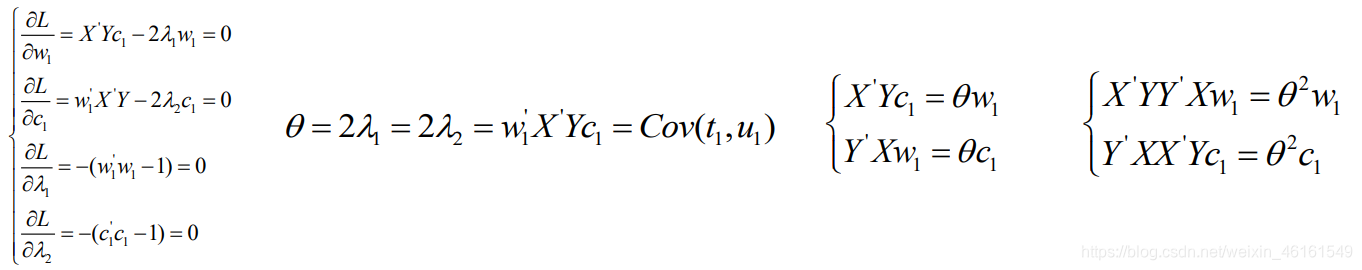
由上式可知，${\text{w}}_1$是矩阵$X^{\prime }Y{Y}^{\prime }X$的特征向量，对应的特征值为${\theta }^2$，使${\mathbf{t}}_1$和${\mathbf{u}}_1$的协方差最大的${\text{w}}_1$是对应矩阵$X^{\prime }Y{Y}^{\prime }X$最大特征值的单位特征向量；
同理，${\mathbf{c}}_1$是矩阵$Y^{\prime }X{X}^{\prime }Y$的特征向量，对应的特征值为${\theta }^2$，使${\mathbf{t}}_1$和${\mathbf{u}}_1$的协方差最大的${\mathbf{c}}_1$是对应矩阵$Y^{\prime }X{X}^{\prime }Y$最大特征值的单位特征向量；

若回归方程的精度已经满足要求，则停止；否则，利用残差矩阵$X^{?}$和$Y^{?}$，计算第二主成分，并重新建立回归方程；以此类推，直到回归方程的精度满足要求为止。

偏最小二乘法建模

%% I. 清空环境变量
clear all
clc

%% II. 导入数据
load spectra;

%% III. 随机划分训练集与测试集
temp = randperm(size(NIR, 1));
% temp = 1:60;
%%
% 1. 训练集——50个样本
P_train = NIR(temp(1:50),:);
T_train = octane(temp(1:50),:);
%%
% 2. 测试集——10个样本
P_test = NIR(temp(51:end),:);
T_test = octane(temp(51:end),:);

%% IV. PLS回归模型
%%
% 1. 创建模型
k = 2;
[Xloadings,Yloadings,Xscores,Yscores,betaPLS,PLSPctVar,MSE,stats] = plsregress(P_train,T_train,k);

%%
% 2. 主成分贡献率分析
figure
percent_explained = 100 * PLSPctVar(2,:) / sum(PLSPctVar(2,:));
pareto(percent_explained)
xlabel('主成分')
ylabel('贡献率(%)')
title('主成分贡献率')

%%
% 3. 预测拟合
N = size(P_test,1);
T_sim = [ones(N,1) P_test] * betaPLS;

%% V. 结果分析与绘图
%%
% 1. 相对误差error
error = abs(T_sim - T_test) ./ T_test;
%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 
%%
% 3. 结果对比
result = [T_test T_sim error]

%% 
% 4. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值','location','best')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)

Fisher LDA(Fisher’s Linear Discriminant Analysis)

• 线性判别分析(Linear DiscriminantAnalysis，LDA)是一种有监督学习算法，由于线性模型对于噪声的鲁棒性比较好，LDA被证明是非常有效的一种降维方法；Fisher 是其中一种分类器准测，

• Fisher LDA的核心思想是最大化类间距离和最小化类内距离

假设有$C_1$、$C_2$两个不同标签的数据，

根据PCA算法进行处理，两个不同类别数据会混合在一起，很难区分开；

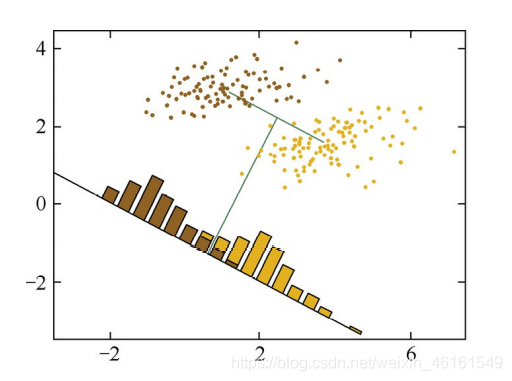
因此提出了Fisher LDA，我们希望处理后的样本尽可能的按照原始类别分开（即，处理后类别之间的距离尽可能大），同时优化样本类别内的方差（即，样本类内方差尽可能小）；

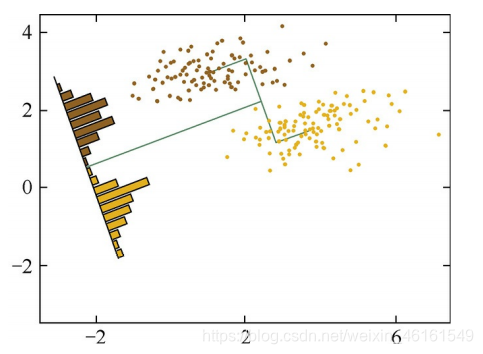
由于Fisher LDA模型简单，表达能力有一定局限性，还可以通过引入核函数扩展LDA方法以处理分布较为复杂的数据

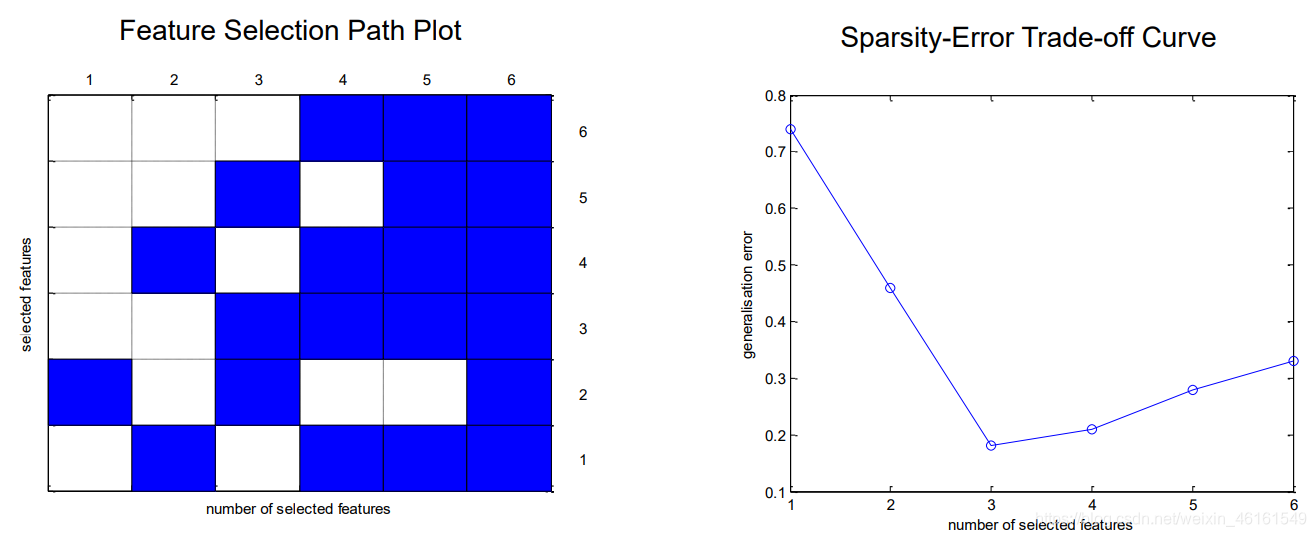
特征选择方法

Filter vs. Wrapper

• Filter无需利用学习模型的性能，即可进行特征选择，主要依赖一些评价准则，如：相关系数、互信息、信息熵等
• Wrapper需要建立学习模型，通过模型的性能进行评价特征的优劣

搜索法

• 随机搜索，如：遗传算法，粒子群算法

  • 遗传算法特征选择
    • 将N个输入变量用一个长度为N的染色体表示，染色体的每一位代表一个输入变量；
    • 每一位的基因取值只能是“1”和“0”两种情况；
    • 如果染色体的某一位值为“1”，表示该位对应的输入变量被选中，参与模型建立；
    • 反之，如果染色体的某一位值为“0”，则表示对应的输入变量未被选中，不参与模型建立；

• 启发式搜索，如：前向选择法、后向选择法

  • 前向选择法

    • 自下而上的选择方法，又称集合增加法；
    • 特征集合初始化为一个空集；
    • 每次向特征集合中添加一个输入变量，当新加入的变量致使模型性能更优时，则保留该输入变量，否则不保留

  • 后向选择法

    • 自上而下的选择方法，又称集合缩减法；
    • 特征集合初始化为全部的输入变量；
    • 每次从特征集合中剔除一个输入变量，当剔除后致使模型性能更优时，则剔除该输入变量，否则保留该 输入变量

正则化方法

• $L_1范数$

• $L_2$范数

特征变量选择的评价