[人工智能]CS224W图机器学习笔记5-消息传递与节点分类

消息传递与节点分类

课程和PPT主页

本文主要解决的问题：给定一个只有部分已知标签节点的图，如何给图中其他节点分配正确的标签？

本文主要讨论一个名为“message passing”的框架以及三个具体的方法：

• Relational classification
• Iterative classification
• Belief propagation

直觉上，相关性(Correlations)总是存在图中：

• 边总是存在相似的节点之间
• 核心概念是collective classification: 将标签同时分配给网络中所有节点

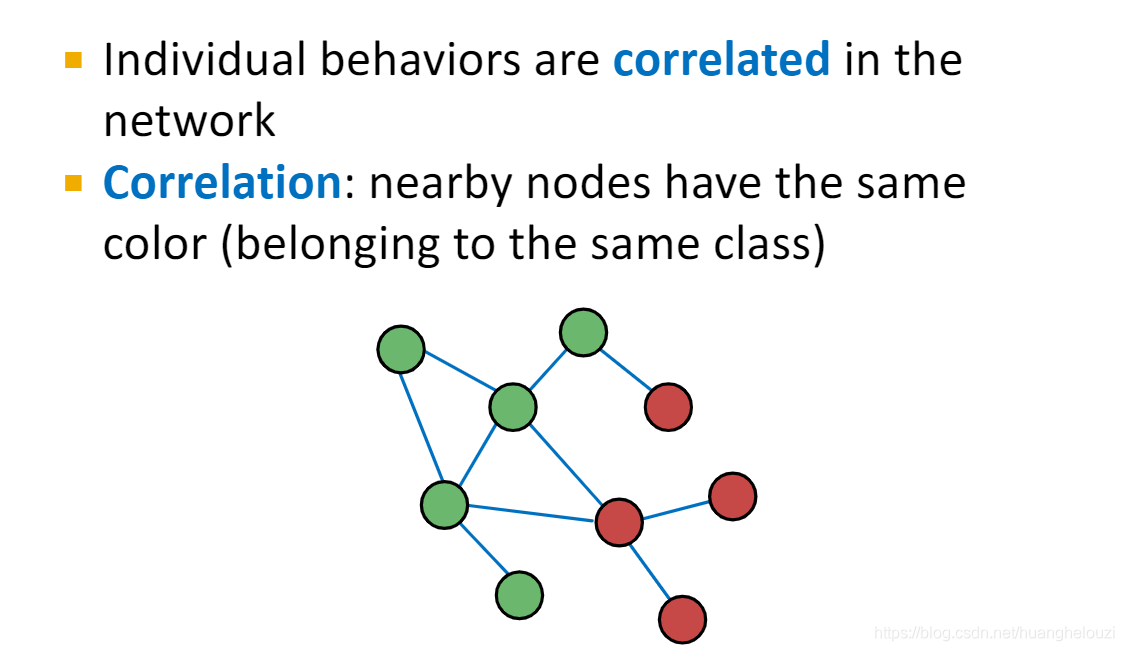
节点间的同质性和总体对节点的影响导致了这种相关性：

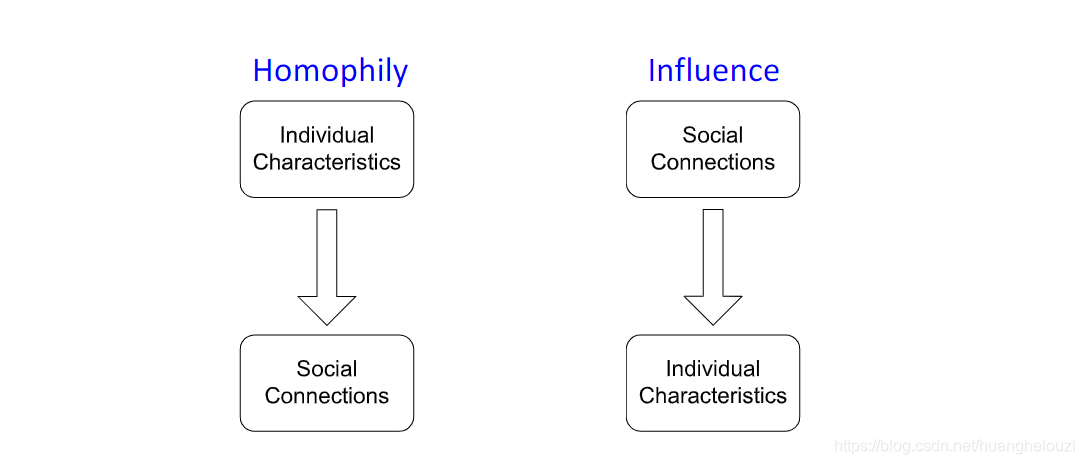
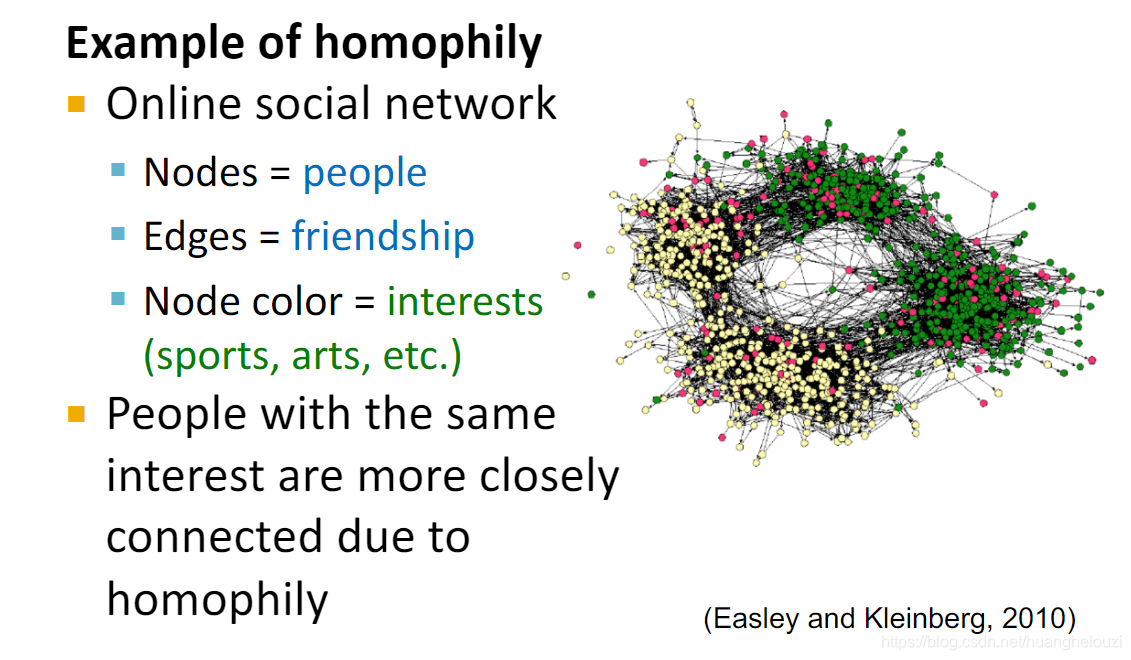
同质性也就是物以类聚的意思：

社交网络是同质性一个很好的例子：


影响也就是总体对个体的影响，类似近朱者赤近墨者黑：

那么怎么利用相似性来帮助我们进行节点分类？也就是预测图中灰色节点的label？

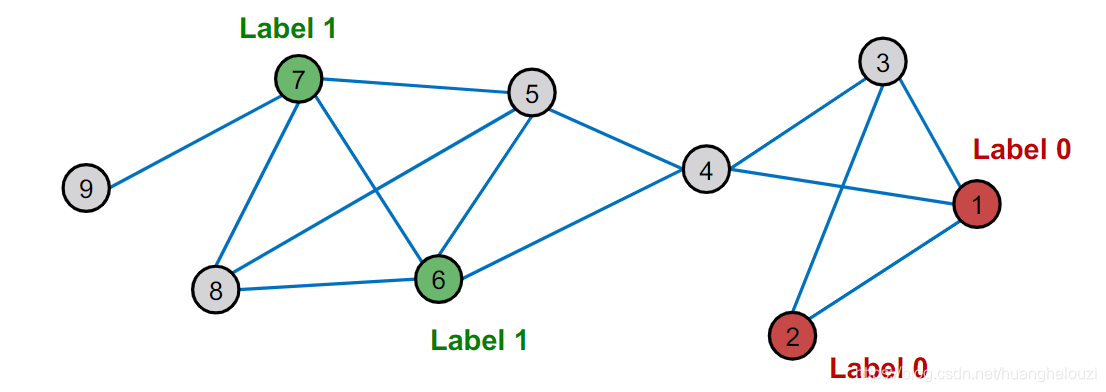
答案主要分为两步：

1. 某个节点和其邻居节点的label大概率相同（物以类聚人以群分）。
   
2. 某个节点的label可能依赖于该节点的特征、邻居节点的label已经邻居节点的特征。
   
   下来介绍一下半监督学习：已知少部分样本已知标签，大部分样本未知，任务是预测剩下大部分样本的标签。
   
   
   对于这些存在相关性的数据，常用的方法是集体分类（Collective Classification，因为节类别依赖其他其他类别，故需要同时预测所有未带标签节点的类型）：考虑一种最简单的情况，节点类别仅与其邻居节点相关，此时可使用马尔科夫假设其该问题进行建模。马尔科夫模型可参考https://blog.csdn.net/pipisorry/article/details/46618991
   
   集体分类可分为三步：
   其中第一步的仅使用节点特征对节点进行分类仅运行一次。第二步可捕获节点相似性，需要在每个节点上迭代运行。
   
   问题Setting：
   
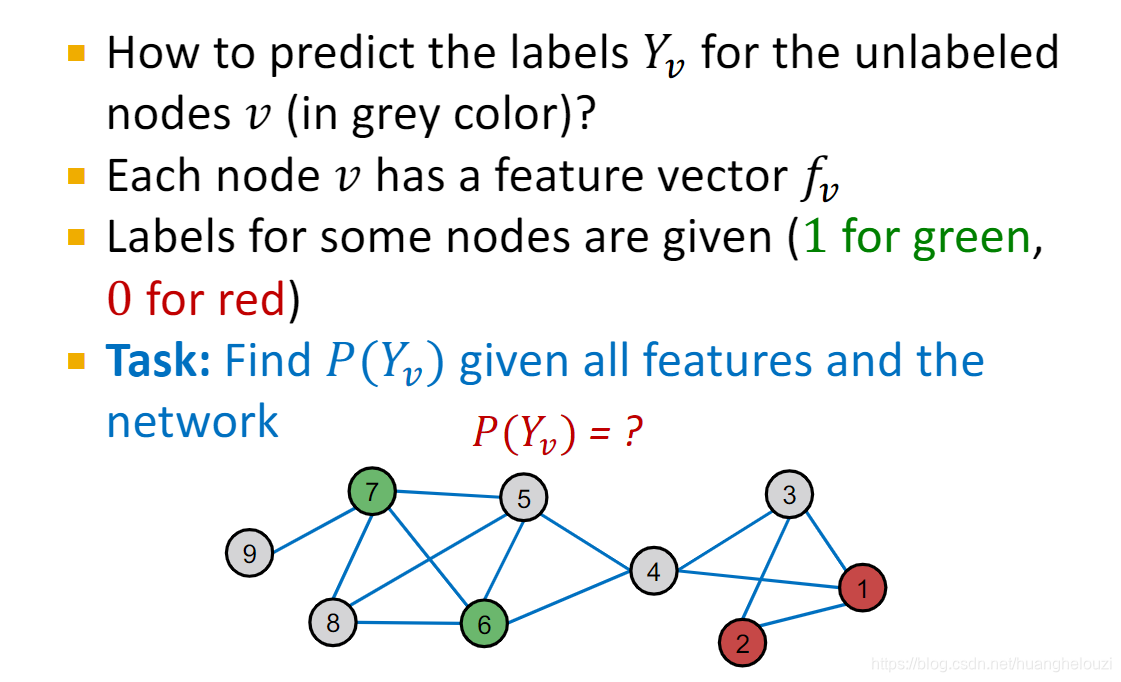
   下面介绍三个集体分类技术：Relational classification、Iterative classification、Belief propagation。

Relational classification

Relational classification只使用邻居节点的label预测节点的label，没有使用到节点feature和邻居节点的feature。

Relational classification可使用在带权图上，当图的边带权时$A_{v,u}$为权值，否则有边取1无边取0。Relational classification有两个缺点：

• 不能保证$P(Y_v=c)$计算公式收敛
• 只能使用邻居节点的label来预测label，没有使用其他的信息（如节点特征）。
  
  下面给出Relational classification的一个例子，图中不同颜色代表不同的类别，我们的任务是预测灰色节点的label。
  初始化：
  
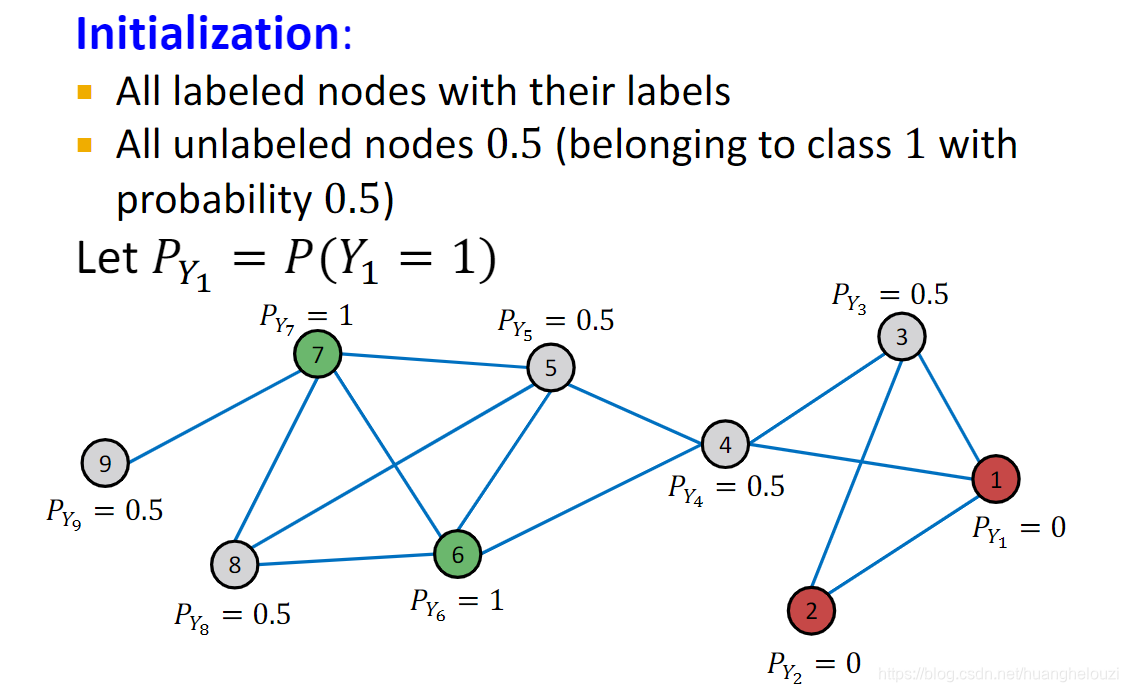
  第一次迭代：这里假设按节点ID从小到大进行计算，其中节点1、2、6、7为带标签节点无需计算，可视为已经收敛。下面给出节点3在第一轮迭代的计算。
  
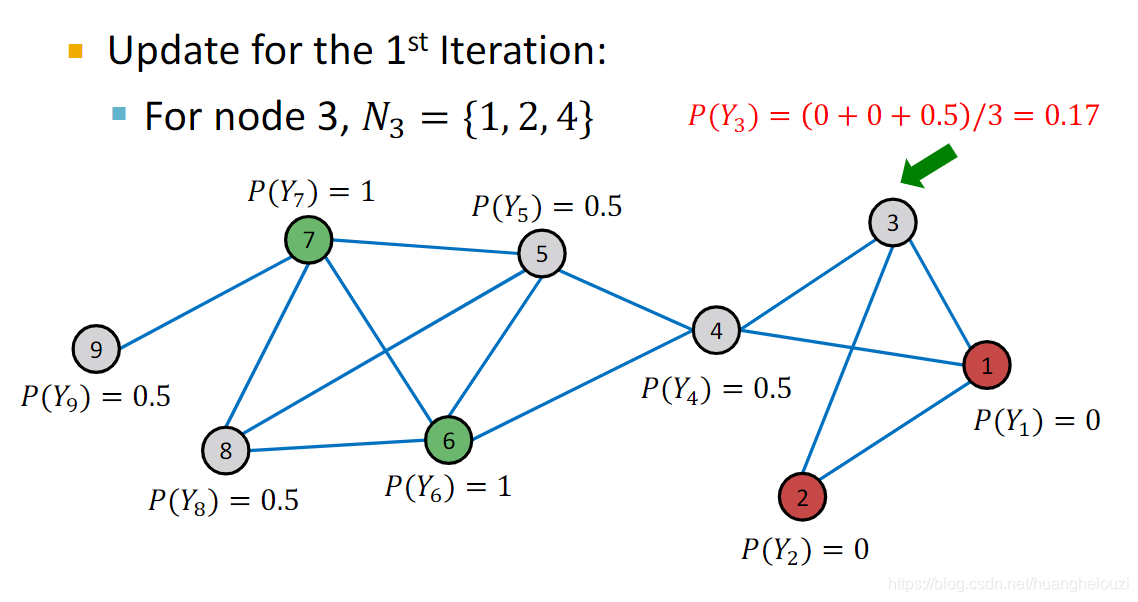
  在计算节点3之后，我们计算节点4的概率。
  
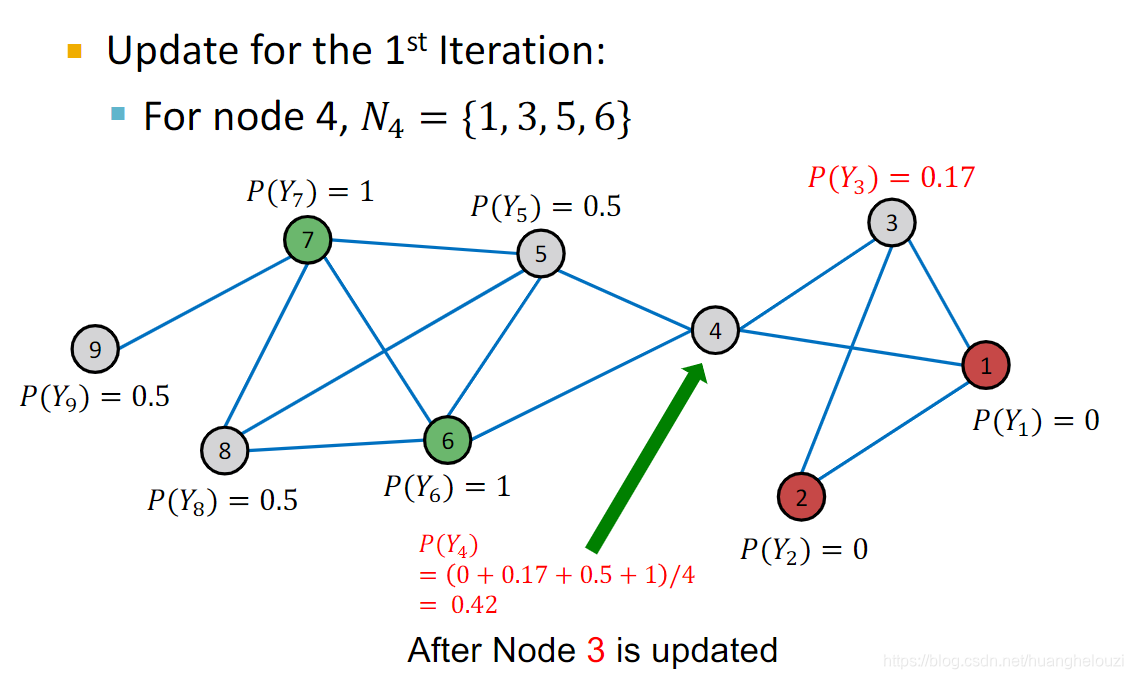
  同理，依次计算其他节点的label，可得到每个节点的概率。
  
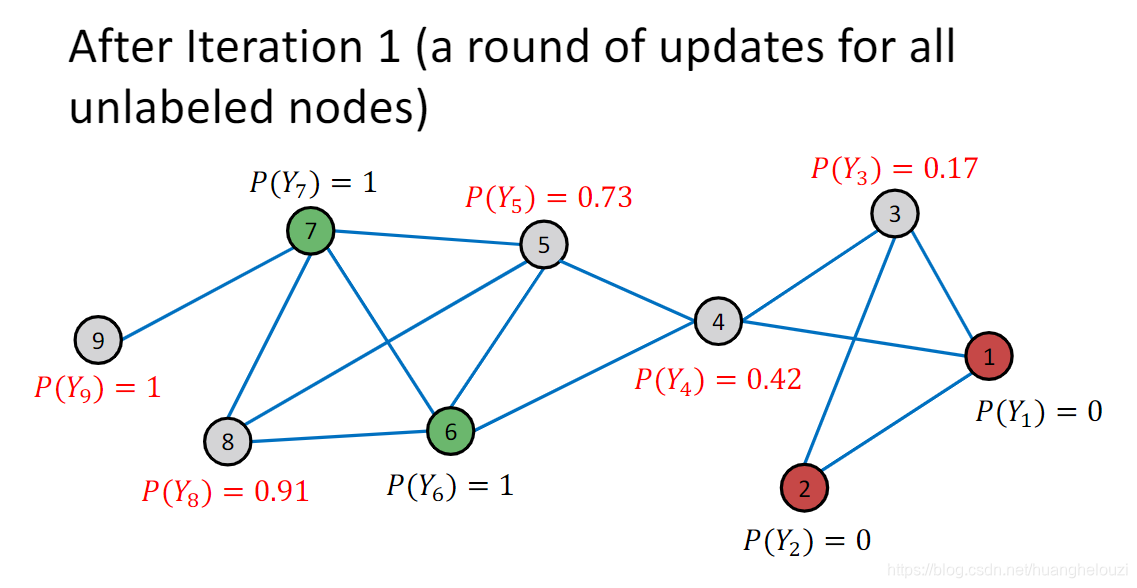
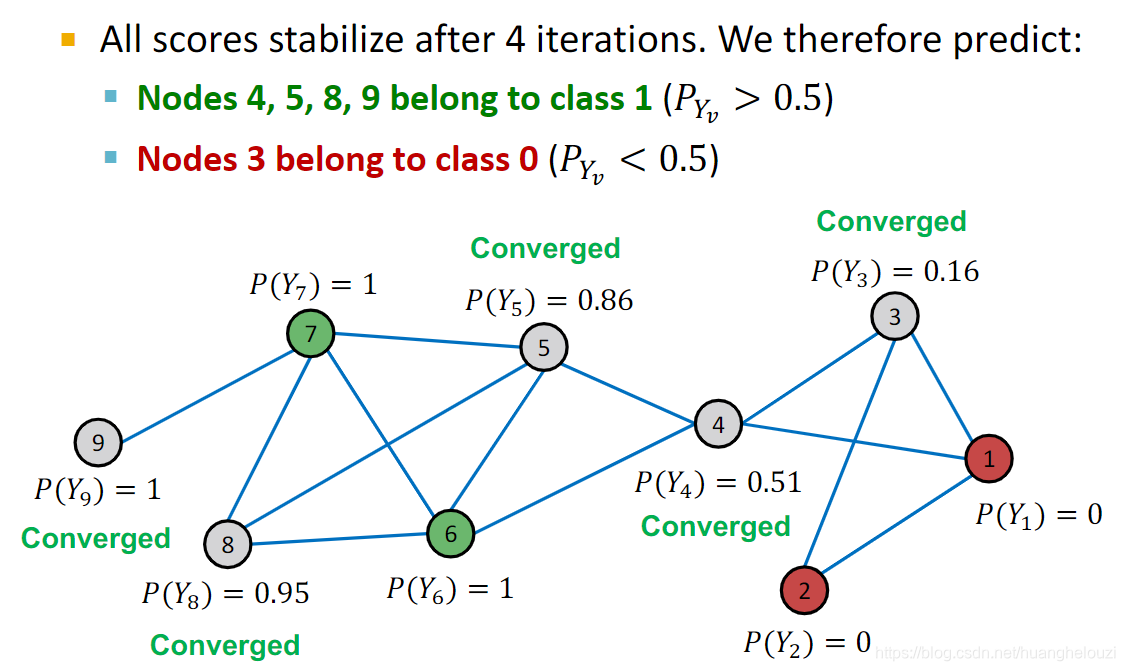
  下面给出第二次迭代的结果，其中的节点9因为仅与已知标签的节点7相连，故节点9概率收敛，在后继迭代中无需计算。
  
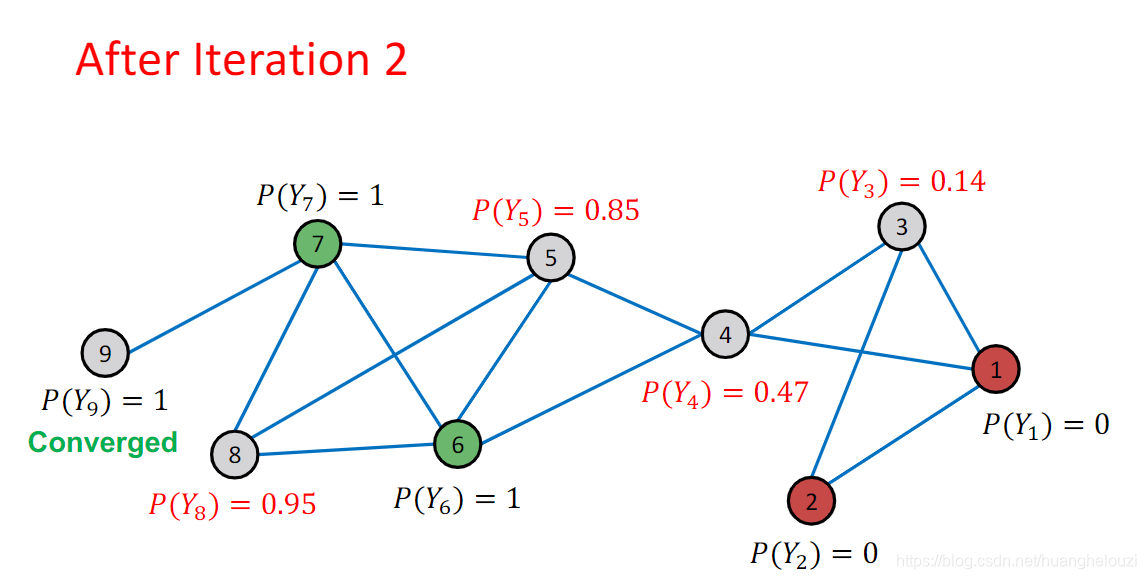
  在第三次迭代中，节点8概率收敛，注：收敛不等同固定，指的是变化在很小的范围。
  
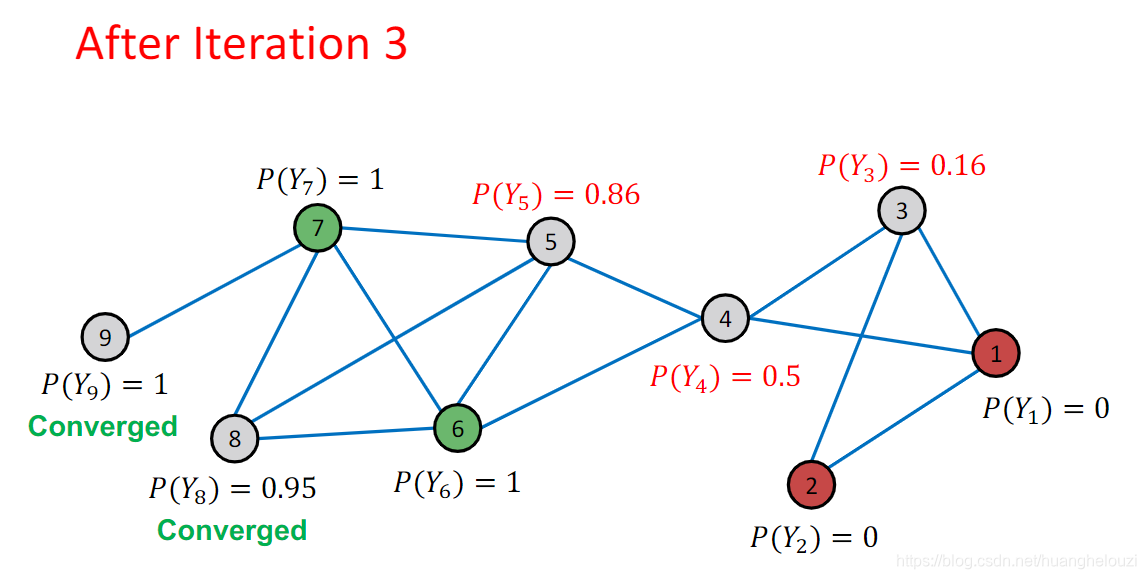
  在多次迭代后，所有节点概率收敛，概率p>0.5的节点认为其属于正类（1），否则视为负类（0）。其中节点4虽然被认为属于正类，但是其概率接近边界值，故该节点分类错误概率最大。
  

Iterative classification

前面也提到，Relational classification的缺点是只使用邻居节点的label预测节点的label，没有使用到节点feature和邻居节点的feature。

而Iterative classification在分类时不仅使用了邻居节点的label，还使用到节点本身的特征。

Iterative classification的做法是训练两个分类器，其中分类器${\Phi }_1$使用节点特征预测节点标签，仅在初始化标签时使用；分类器${\Phi }_2$同时使用节点特征和邻居节点的标签概括向量$z_v$预测节点标签，迭代多次使用。

那么怎么计算邻居节点的标签概括向量$z_v$呢？方法有很多种，比如邻居节点标签的众数等。

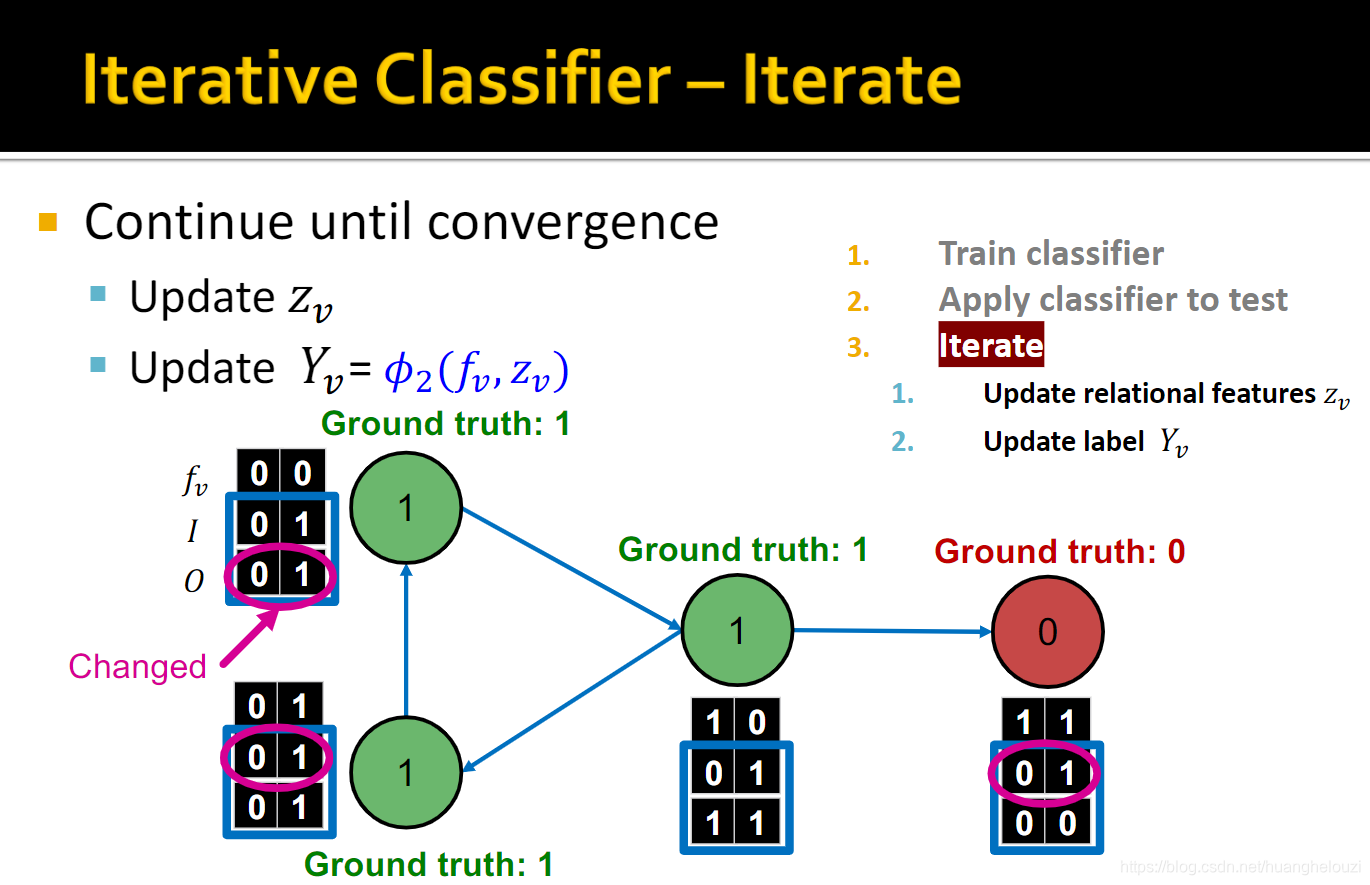
下面给出Iterative classification方案的框架，一共可分为两步，需要注意的是：因为迭代过程不一定收敛，故需要设置最大迭代次数，可以是一个比较大的数，比如100，500。

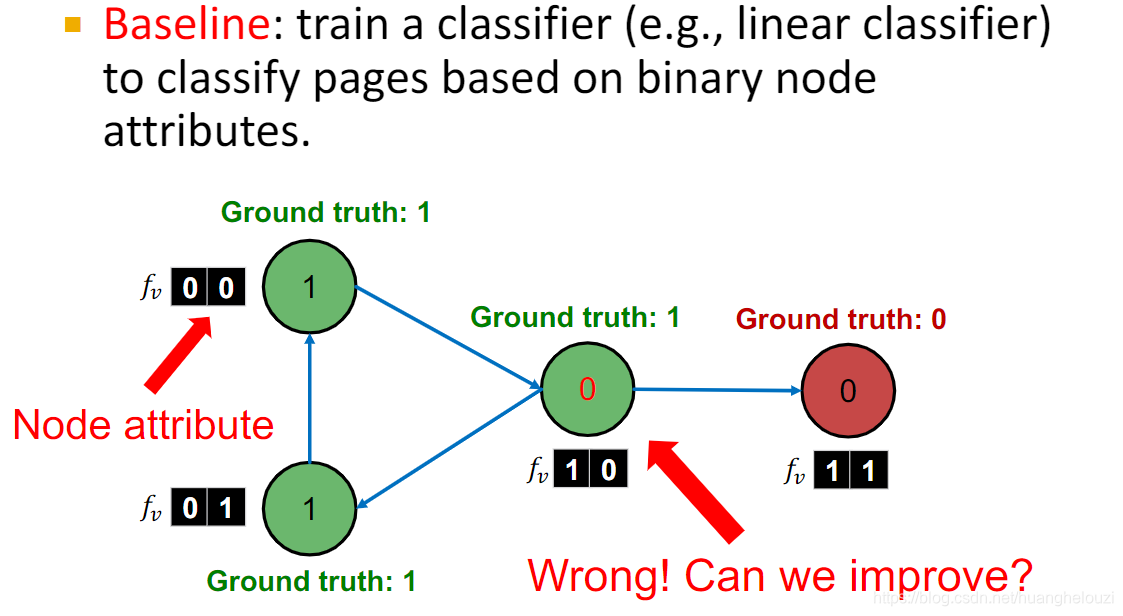
下面给出关于Relational classification的例子：web网页分类。

如果我们仅使用节点特征训练分类器，由于没有利用到网络结构信息，所以比较容易分类错误，如下图中中间那个节点真实标签为1，但是分类器可能将其判断为0。该分类器也就是分类器${\Phi }_1$，在为每个节点初始化标签后不再使用。

一个改进方案是使用节点特征和邻居节点标签共同训练分类器。$I$和$O$共同组成邻居节点的标签概括向量$z_v$，$z_v$基于分类器${\Phi }_1$预测类别构建。

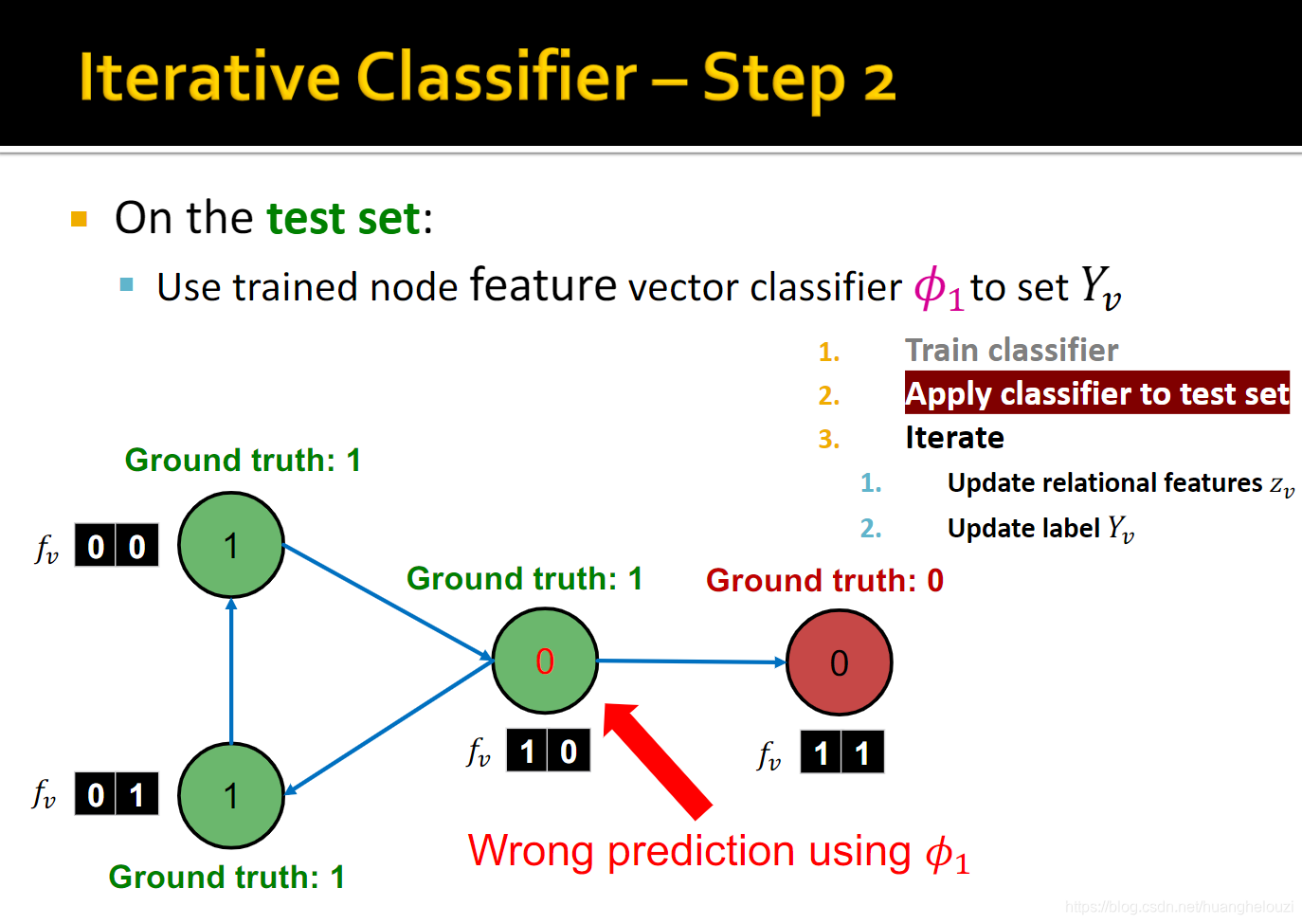
Relational classification运行流程如下：

1. 首先训练两个分类器：
   
2. 使用分类器${\Phi }_1$设置初始化标签
   
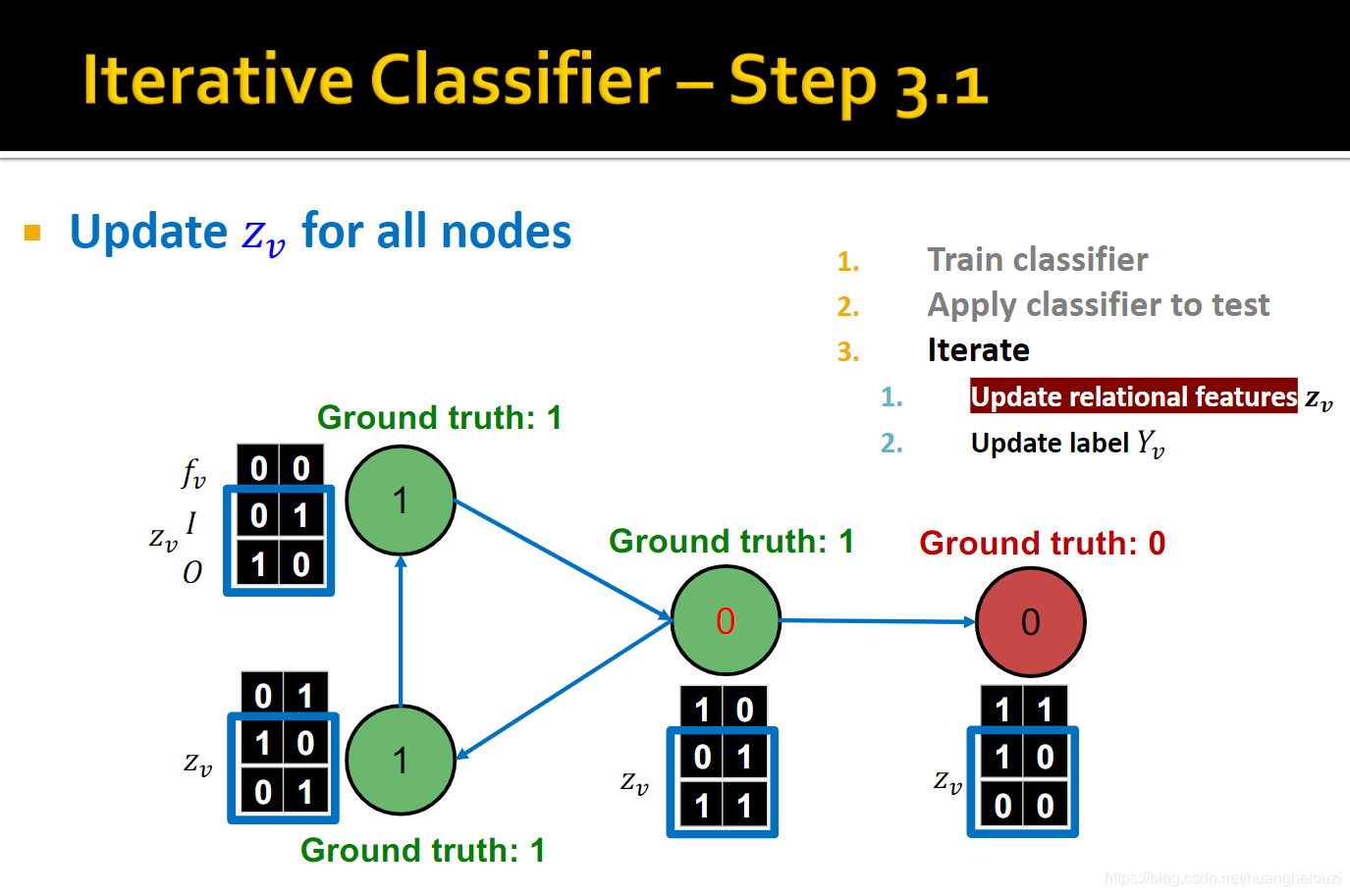
3. 使用分类器${\Phi }_1$设置的初始化标签构建标签概括向量$z_v$
   
   使用分类器${\Phi }_2$更新节点标签
   
   迭代更新节点标签和标签概括向量$z_v$，直到收敛或者超出最大迭代次数。
   
   
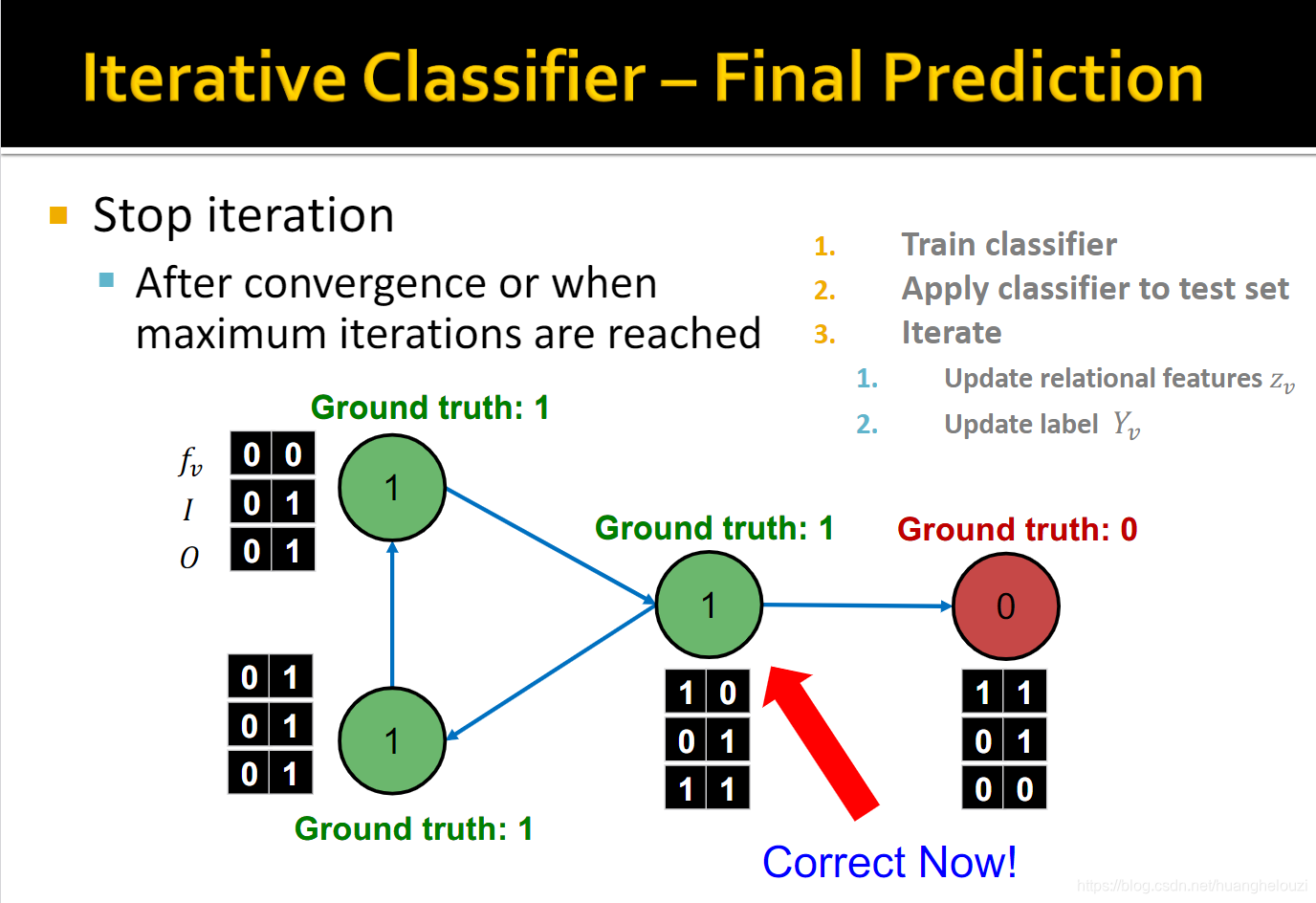
   然后对Relational classification和Iterative classification进行小结。
   

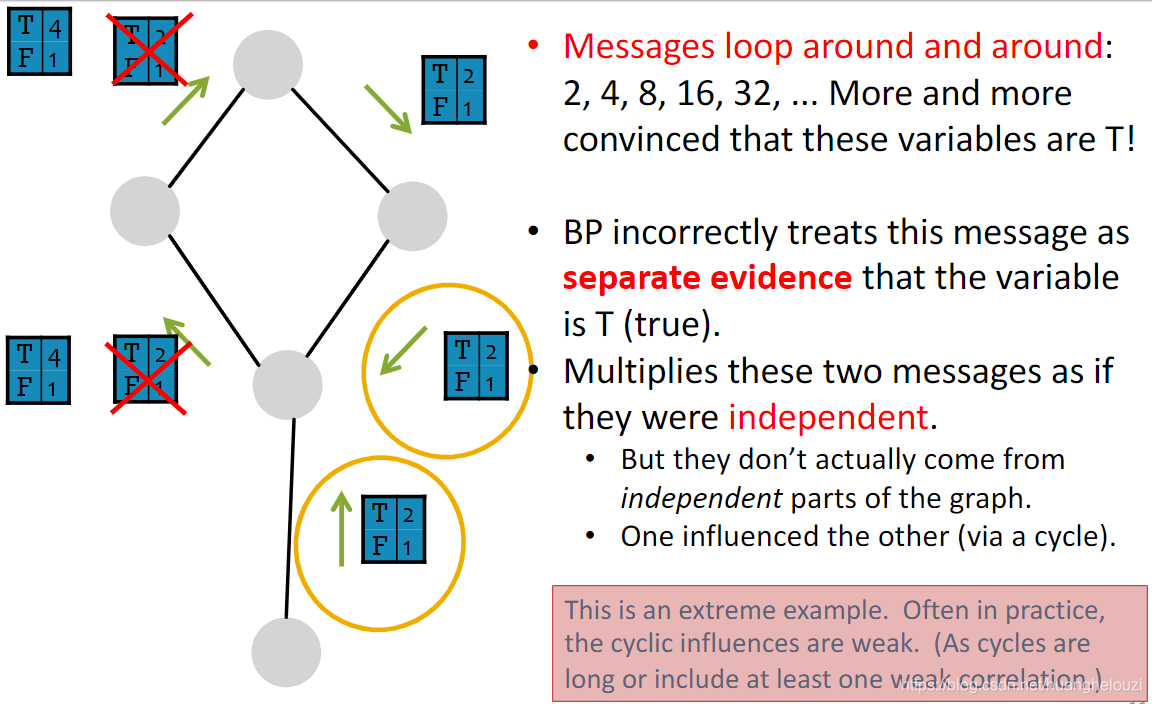
Loopy Belief Propagation

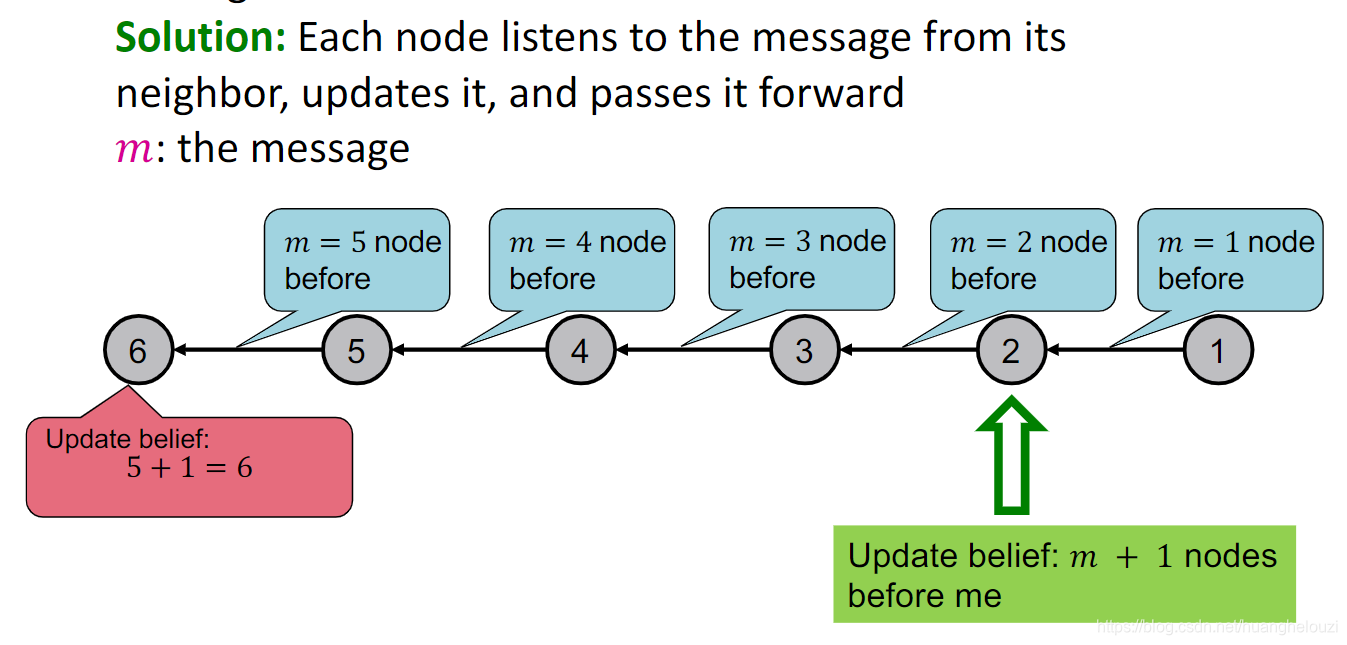
下面使用几个“计数”的例子，来解释说明消息传递（pass message）。注意：该过程中不可出现环路且只能和直接邻居节点进行交互。第一个例子使用一个path graph，这个和军训时排队报数的过程十分相似。

各个节点间传递的东西被称为信息（message），故整个过程被称为“pass message”

下面提供另外一个“计数”例子，从path graph扩展到树形图(tree-structured graph)。

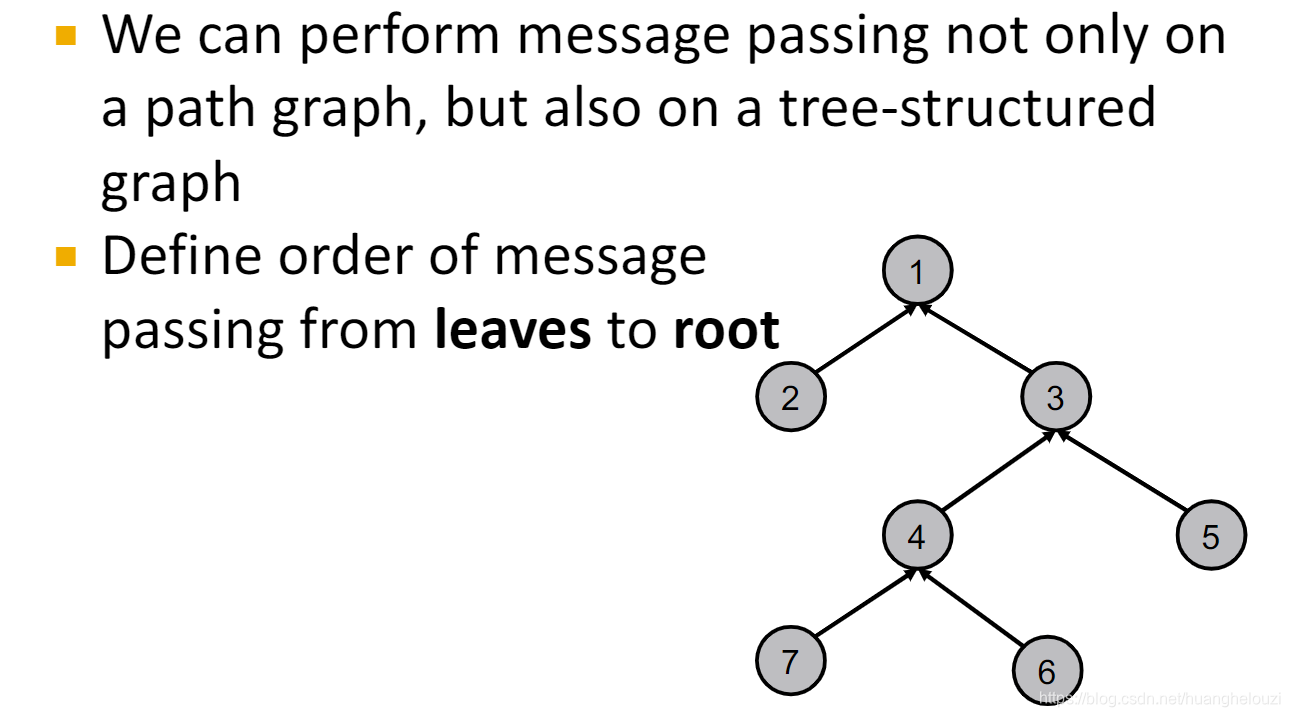
消息传递过程和path graph十分类似。


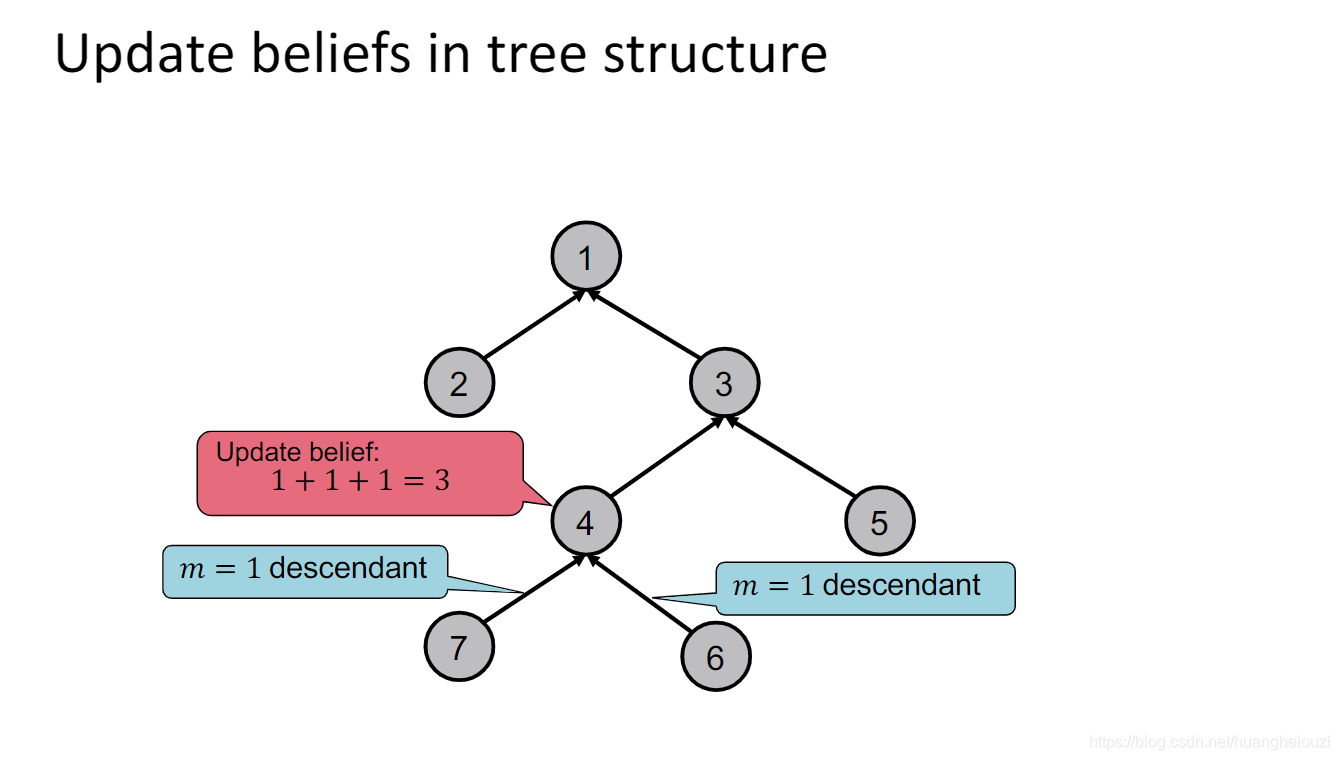
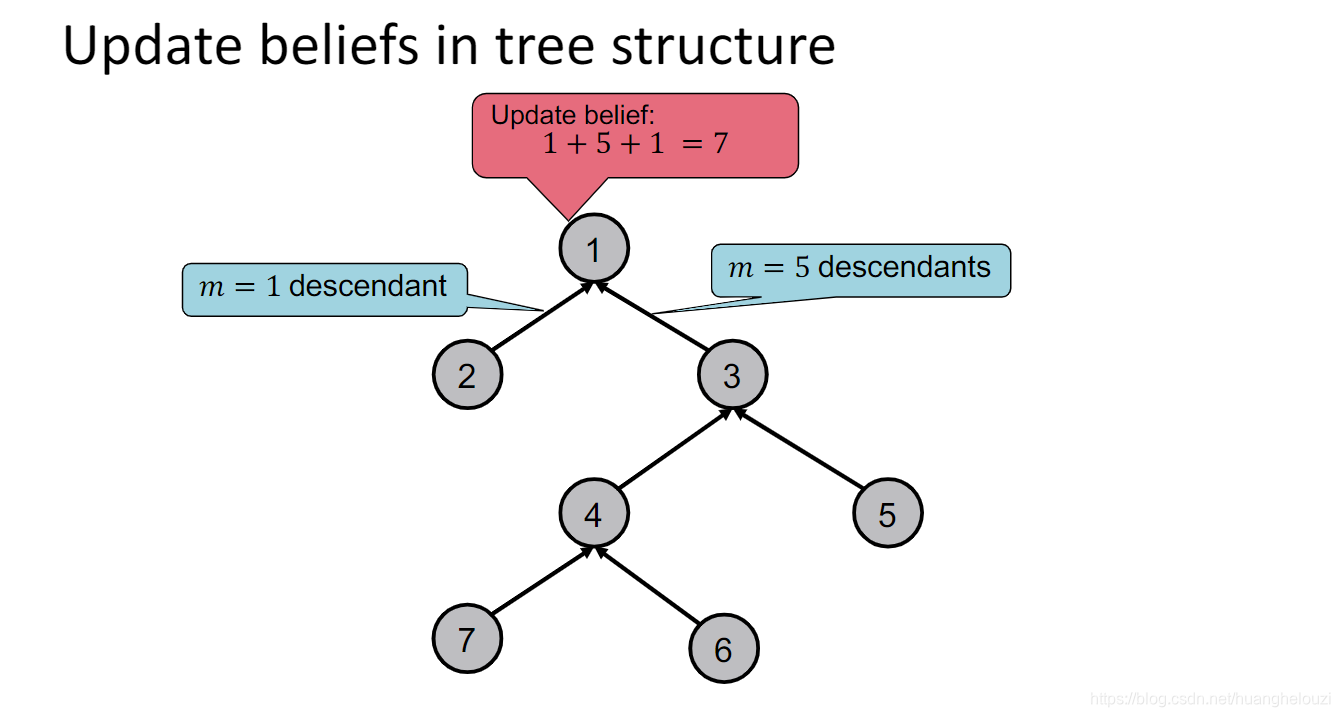
从上述两个例子中，可以发现message不是随意定义的，message依赖于节点的邻居节点。如下图中，节点$i$的message依赖于节点$k$、节点$u$、节点$v$传递过来的message，同理节点$j$的message也依赖于节点$i$的message。

下面给出Loopy BP Algorithm正式描述，（我没怎么看懂）。



下面是Loopy BP Algorithm的例子：



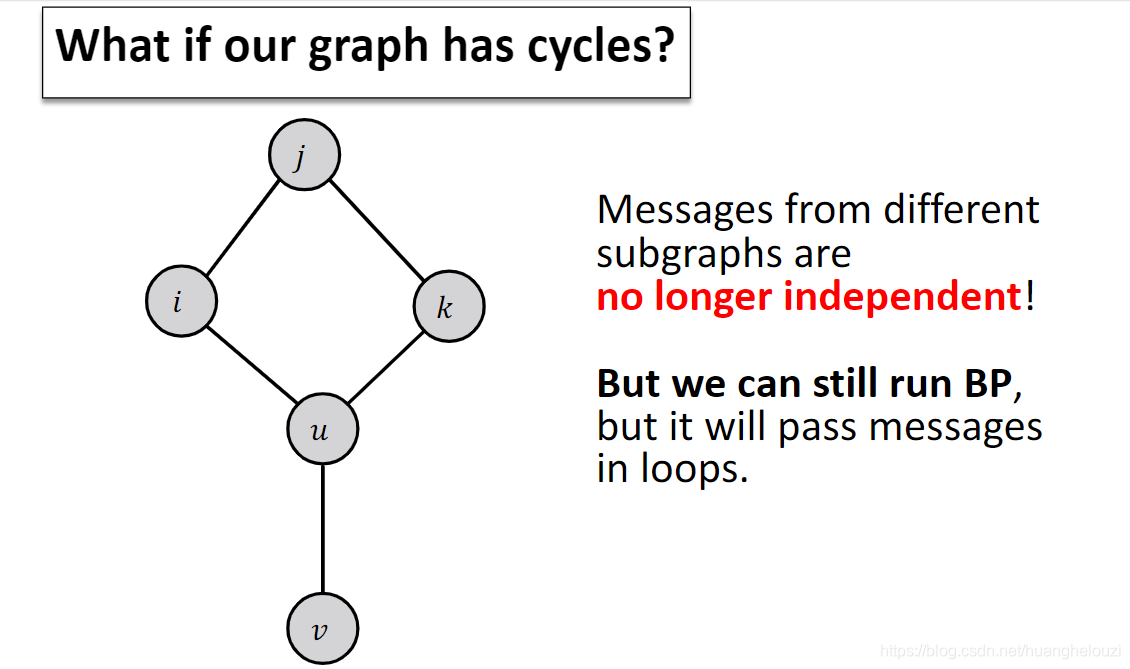
由于现实世界中的图通常长得比较想树形图，回路比较少，故可以使用前面的方法近似计算。