29. 多元分析
定义
多元分析是多变量的统计分析方法,是数理统计中应用广泛的一个重要分支。
判别分析
判别分析是一种分类方法。假定有
r
r
r 类判别对象
A
1
,
A
2
,
…
,
A
r
A_1,A_2,\dots,A_r
A1?,A2?,…,Ar?,每一类
A
i
A_i
Ai? 由
m
m
m 个指标的
n
i
n_i
ni? 个样本确定,即
A
i
=
(
a
11
(
i
)
a
12
(
i
)
…
a
1
m
(
i
)
a
21
(
i
)
a
22
(
i
)
…
a
2
m
(
i
)
?
?
?
?
a
n
i
1
(
i
)
a
n
i
2
(
i
)
…
a
n
i
m
(
i
)
)
=
(
(
a
1
(
i
)
)
T
(
a
2
(
i
)
)
T
?
(
a
n
i
(
i
)
)
T
)
,
A_i=\begin{pmatrix} a_{11}^{(i)}&a_{12}^{(i)}&\dots&a_{1m}^{(i)}\\ a_{21}^{(i)}&a_{22}^{(i)}&\dots&a_{2m}^{(i)}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n_i1}^{(i)}&a_{n_i2}^{(i)}&\dots&a_{n_im}^{(i)}\\ \end{pmatrix}=\begin{pmatrix} (a_1^{(i)})^T\\ (a_2^{(i)})^T\\ \vdots\\ (a_{n_i}^{(i)})^T\\ \end{pmatrix},
Ai?=???????a11(i)?a21(i)??ani?1(i)??a12(i)?a22(i)??ani?2(i)??……?…?a1m(i)?a2m(i)??ani?m(i)?????????=???????(a1(i)?)T(a2(i)?)T?(ani?(i)?)T????????,
其中
A
i
A_i
Ai? 矩阵的第
k
k
k 行是
A
i
A_i
Ai? 的第
k
k
k 个样本点的观测值向量。
记
n
=
∑
i
=
1
r
n
i
n=\sum_{i=1}^rn_i
n=∑i=1r?ni?,
μ
i
,
L
i
\mu_i,L_i
μi?,Li? 分别表示
A
i
A_i
Ai?? 的均值向量和离差矩阵,即
μ
i
=
1
n
i
∑
k
=
1
n
i
a
k
(
i
)
,
\mu_i=\frac1{n_i}\sum_{k=1}^{n_i}a_k^{(i)},
μi?=ni?1?k=1∑ni??ak(i)?,
L i = ∑ k = 1 n i ( a k ( i ) ? μ i ) ( a k ( i ) ? μ i ) T . L_i=\sum_{k=1}^{n_i}(a_k^{(i)}-\mu_i)(a_k^{(i)}-\mu_i)^T. Li?=k=1∑ni??(ak(i)??μi?)(ak(i)??μi?)T.
对待判定对象 x = ( x 1 , x 2 , … , x m ) T x=(x_1,x_2,\dots,x_m)^T x=(x1?,x2?,…,xm?)T?,有一个一般规则,可以依据 x x x? 的值,对 x x x? 属于 A i A_i Ai? 的哪一类作出判别,称判别规则,其函数称判别函数,记 W ( i , x ) , i = 1 , 2 , … , r W(i,x),i=1,2,\dots,r W(i,x),i=1,2,…,r。
距离判别法
根据距离最近原则判别。
W
(
i
,
x
)
=
d
(
x
,
A
i
)
,
W(i,x)=d(x,A_i),
W(i,x)=d(x,Ai?),
若
W
(
k
,
x
)
=
min
?
{
W
(
i
,
x
)
∣
i
=
1
,
2
,
…
,
r
}
W(k,x)=\min\{W(i,x)|i=1,2,\dots,r\}
W(k,x)=min{W(i,x)∣i=1,2,…,r}
则
x
∈
A
k
x\in A_k
x∈Ak?。
距离
d
(
x
,
A
i
)
d(x,A_i)
d(x,Ai?) 一般用马氏距离,
r
r
r 个总体协方差矩阵相等时
d
(
x
,
A
i
)
=
(
(
x
?
μ
i
)
T
Σ
?
1
(
x
?
μ
i
)
)
1
2
,
d(x,A_i)=((x-\mu_i)^T\Sigma^{-1}(x-\mu_i))^{\frac12},
d(x,Ai?)=((x?μi?)TΣ?1(x?μi?))21?,
Σ = 1 n ? r ∑ i = 1 r L i , \Sigma=\frac{1}{n-r}\sum_{i=1}^rL_i, Σ=n?r1?i=1∑r?Li?,
不等时
d
(
x
,
A
i
)
=
(
x
?
μ
i
)
T
Σ
i
?
1
(
x
?
μ
i
)
,
d(x,A_i)=\sqrt{(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)},
d(x,Ai?)=(x?μi?)TΣi?1?(x?μi?)?,
Σ i = 1 n i ? 1 L i . \Sigma_i=\frac{1}{n_i-1}L_i. Σi?=ni??11?Li?.
Fisher 判别法
Fisher 判别法的思想是,将样例投影到一条或多条直线上,使同类样例的投影点尽可能接近,不同类样例的投影点尽可能远离。
对于二分类情况,若给定直线 y = w T x y=w^Tx y=wTx???,则第 i i i? 类样本的中心在直线上的投影为 w T μ i w^T\mu_i wTμi??。
第
i
i
i? 类中第
a
k
(
i
)
a_k^{(i)}
ak(i)?? 个样本的组内偏差为
(
w
T
a
k
(
i
)
?
w
T
μ
i
)
2
(w^Ta_k^{(i)}-w^T\mu_i)^2
(wTak(i)??wTμi?)2?,故第
i
i
i? 类的组内偏差之和为
∑
k
=
1
n
i
(
w
T
a
k
(
i
)
?
w
T
μ
i
)
2
\sum_{k=1}^{n_i}(w^Ta_k^{(i)}-w^T\mu_i)^2
k=1∑ni??(wTak(i)??wTμi?)2
= ∑ k = 1 n i w T ( a k ( i ) ? μ i ) ( a k ( i ) ? μ i ) T w =\sum_{k=1}^{n_i}w^T(a_k^{(i)}-\mu_i)(a_k^{(i)}-\mu_i)^Tw =k=1∑ni??wT(ak(i)??μi?)(ak(i)??μi?)Tw
去掉
w
w
w 得
L
i
=
∑
k
=
1
n
i
(
a
k
(
i
)
?
μ
i
)
(
a
k
(
i
)
?
μ
i
)
T
,
L_i=\sum_{k=1}^{n_i}(a_k^{(i)}-\mu_i)(a_k^{(i)}-\mu_i)^T,
Li?=k=1∑ni??(ak(i)??μi?)(ak(i)??μi?)T,
即离差矩阵。
所有类的组内偏差总和即为
L
=
L
1
+
L
2
.
L=L_1+L_2.
L=L1?+L2?.
要使同类样例的投影点尽可能接近,只需使
w
T
L
w
w^TLw
wTLw?? 最小化。
而组间偏差同理有
B
=
(
μ
1
?
μ
0
)
(
μ
1
?
μ
0
)
T
B=(\mu_1-\mu_0)(\mu_1-\mu_0)^T
B=(μ1??μ0?)(μ1??μ0?)T
要使不同类样例的投影点尽可能远离,只需使
w
T
B
w
w^TBw
wTBw?? 最大化。
于是构造代价函数
J
=
w
T
B
w
w
T
L
w
,
J=\frac{w^TBw}{w^TLw},
J=wTLwwTBw?,
使得
J
J
J? 最大,也就等价于
min
?
w
?
w
T
B
w
,
\min_w-w^TBw,
wmin??wTBw,
s . t . : w T L w = 1. s.t.:w^TLw=1. s.t.:wTLw=1.
根据拉格朗日乘子法,即
L
(
w
)
=
?
w
T
B
w
+
λ
(
w
T
L
w
?
1
)
L(w)=-w^TBw+\lambda(w^TLw-1)
L(w)=?wTBw+λ(wTLw?1)
则
?
L
?
w
=
?
2
B
w
+
2
λ
L
w
=
0
,
\frac{\partial L}{\partial w}=-2Bw+2\lambda Lw=0,
?w?L?=?2Bw+2λLw=0,
得
S
b
w
=
λ
L
w
S_bw=\lambda Lw
Sb?w=λLw,即
w
w
w 为矩阵
L
?
1
B
L^{-1}B
L?1B? 的特征向量。于是
w
=
1
λ
L
?
1
(
μ
1
?
μ
0
)
(
μ
1
?
μ
0
)
T
w
w=\frac1\lambda L^{-1}(\mu_1-\mu_0)(\mu_1-\mu_0)^Tw
w=λ1?L?1(μ1??μ0?)(μ1??μ0?)Tw
→ L ? 1 ( μ 1 ? μ 0 ) . \to L^{-1}(\mu_1-\mu_0). →L?1(μ1??μ0?).
于是有直线 y = w T x y=w^Tx y=wTx,和 w w w?? 垂直的两类的中心线可作为两类的判别直线。
即有阈值 w 0 = w T μ 0 + w T μ 1 2 w_0=\frac{w^T\mu_0+w^T\mu_1}{2} w0?=2wTμ0?+wTμ1????,比较 y y y? 与 w 0 w_0 w0?? 的大小,得出分类。
对于多分类情况,则有
B
=
∑
i
=
1
r
(
μ
i
?
μ
)
(
μ
i
?
μ
)
T
,
B=\sum_{i=1}^r(\mu_i-\mu)(\mu_i-\mu)^T,
B=i=1∑r?(μi??μ)(μi??μ)T,
μ = 1 r ∑ i = 1 r u i \mu=\frac{1}{r}\sum_{i=1}^ru_i μ=r1?i=1∑r?ui?
之后求解
B
W
=
λ
L
W
BW=\lambda LW
BW=λLW
W
W
W 的闭式解为
L
?
1
B
L^{-1}B
L?1B? 的
r
?
1
r-1
r?1 个最大广义特征值所对应的特征向量组成的矩阵。
主成分分析
主成分分析,是利用降维把多指标转化为几个综合指标的多元统计分析方法。
设
X
1
,
X
2
,
…
,
X
m
X_1,X_2,\dots,X_m
X1?,X2?,…,Xm? 表示以
x
1
,
x
2
,
…
,
x
m
x_1,x_2,\dots,x_m
x1?,x2?,…,xm?? 为样本观测值的随机变量,如果能找到
c
1
,
c
2
,
…
,
c
m
c_1,c_2,\dots,c_m
c1?,c2?,…,cm?,使得方差
V
a
r
(
c
1
X
1
+
c
2
X
2
+
?
+
c
m
X
m
)
Var(c_1X_1+c_2X_2+\dots+c_mX_m)
Var(c1?X1?+c2?X2?+?+cm?Xm?)
最大,就表明这
m
m
m 个变量的最大差异。
一般说来,代表原来 m m m? 个变量的主成分不止一个,但不同主成分的信息不能相互包含,即协方差为 0,在几何上即方向正交。
设
F
i
F_i
Fi? 表示第
i
i
i 个主成分
F
i
=
c
i
1
X
1
+
c
i
2
X
2
+
?
+
c
i
m
X
m
,
i
=
1
,
2
,
…
,
m
,
F_i=c_{i1}X_1+c_{i2}X_2+\dots+c_{im}X_m,i=1,2,\dots,m,
Fi?=ci1?X1?+ci2?X2?+?+cim?Xm?,i=1,2,…,m,
其中
∑
j
=
1
m
c
i
j
2
=
1
\sum_{j=1}^mc_{ij}^2=1
∑j=1m?cij2?=1,
c 1 = ( c 11 , … , c 1 m ) T c_1=(c_{11},\dots,c_{1m})^T c1?=(c11?,…,c1m?)T 使 V a r ( F 1 ) Var(F_1) Var(F1?)? 最大,?
c 2 = ( c 21 , … , c 2 m ) c_2=(c_{21},\dots,c_{2m}) c2?=(c21?,…,c2m?) 使 c 2 ⊥ c 1 c_2\bot c_1 c2?⊥c1? 并使 V a r ( F 2 ) Var(F2) Var(F2)????? 最大,
c 3 = ( c 31 , … , c 3 m ) c_3=(c_{31},\dots,c_{3m}) c3?=(c31?,…,c3m?)? 使 c 3 ⊥ c 1 , c 3 ⊥ c 2 c_3\bot c_1,c_3\bot c_2 c3?⊥c1?,c3?⊥c2? 并使 V a r ( F 3 ) Var(F3) Var(F3)? 最大,
……
为实现上述目标,步骤如下:
-
假设有 n n n? 个对象, m m m? 个指标 x 1 , x 2 , … , x m x_1,x_2,\dots,x_m x1?,x2?,…,xm?,设第 i i i 个对象的第 j j j 个指标为 a i j a_{ij} aij?,对原来的 m m m??? 个指标进行标准化
b i j = a i j ? μ j s j , j = 1 , 2 , … , m , b_{ij}=\frac{a_{ij}-\mu_j}{s_j},j=1,2,\dots,m, bij?=sj?aij??μj??,j=1,2,…,m,
其中
μ j = 1 n ∑ i = 1 n a i j , s j = 1 n ? 1 ∑ i = 1 n ( a i j ? μ j ) 2 , \mu_j=\frac1n\sum_{i=1}^na_{ij},s_j=\sqrt{\frac{1}{n-1}\sum_{i=1}^n(a_{ij}-\mu_j)^2}, μj?=n1?i=1∑n?aij?,sj?=n?11?i=1∑n?(aij??μj?)2?,
得标准化的数据矩阵 B = ( b i j ) n × m B=(b_{ij})_{n\times m} B=(bij?)n×m???,记标准化后的指标为 y i y_i yi?; -
求相关系数矩阵 R = ( r i j ) m × m R=(r_{ij})_{m\times m} R=(rij?)m×m?,
r i j = ∑ k = 1 n b k i b k j n ? 1 , i , j = 1 , 2 , … m . r_{ij}=\frac{\sum_{k=1}^nb_{ki}b_{kj}}{n-1},i,j=1,2,\dots m. rij?=n?1∑k=1n?bki?bkj??,i,j=1,2,…m. -
计算相关系数矩阵 R R R 的特征值 λ 1 ≥ λ 2 ≥ ? ≥ λ m \lambda_1\ge\lambda_2\ge\dots\ge\lambda_m λ1?≥λ2?≥?≥λm? 及对应的标准正交化特征向量 u 1 , u 2 , … , u m u_1,u_2,\dots,u_m u1?,u2?,…,um?,其中 u j = ( u 1 j , … , u m j ) T u_j=(u_{1j},\dots,u_{mj})^T uj?=(u1j?,…,umj?)T,组成 m m m 个新的指标变量
{ F 1 = u 11 y 1 + u 21 y 2 + ? + u m 1 y m , F 2 = u 12 y 1 + u 22 y 2 + ? + u m 2 y m , … F m = u 1 m y 1 + u 2 m y 2 + ? + u m m y m . \left\{\begin{aligned} &F_1=u_{11}y_1+u_{21}y_2+\dots+u_{m1}y_m,\\ &F_2=u_{12}y_1+u_{22}y_2+\dots+u_{m2}y_m,\\ &\dots\\ &F_m=u_{1m}y_1+u_{2m}y_2+\dots+u_{mm}y_m.\\ \end{aligned}\right. ?????????????F1?=u11?y1?+u21?y2?+?+um1?ym?,F2?=u12?y1?+u22?y2?+?+um2?ym?,…Fm?=u1m?y1?+u2m?y2?+?+umm?ym?.? -
计算主成分贡献率
w j = λ j ∑ k = 1 m λ k , j = 1 , 2 , … , m , w_j=\frac{\lambda_j}{\sum_{k=1}^m\lambda_k},j=1,2,\dots,m, wj?=∑k=1m?λk?λj??,j=1,2,…,m,
累计贡献率
∑ k = 1 i λ k ∑ k = 1 m λ k . \frac{\sum_{k=1}^i\lambda_k}{\sum_{k=1}^m\lambda_k}. ∑k=1m?λk?∑k=1i?λk??.
因子分析
因子分析将原始变量分解为若干个因子的线性组合
{
x
1
=
μ
1
+
a
11
f
1
+
a
12
f
2
+
?
+
a
1
p
f
p
+
ε
1
,
x
2
=
μ
2
+
a
21
f
1
+
a
22
f
2
+
?
+
a
2
p
f
p
+
ε
2
,
…
x
m
=
μ
m
+
a
m
1
f
1
+
a
m
2
f
2
+
?
+
a
m
p
f
p
+
ε
m
,
\left\{\begin{aligned} &x_1=\mu_1+a_{11}f_1+a_{12}f_2+\dots+a_{1p}f_p+\varepsilon_1,\\ &x_2=\mu_2+a_{21}f_1+a_{22}f_2+\dots+a_{2p}f_p+\varepsilon_2,\\ &\dots\\ &x_m=\mu_m+a_{m1}f_1+a_{m2}f_2+\dots+a_{mp}f_p+\varepsilon_m,\\ \end{aligned}\right.
?????????????x1?=μ1?+a11?f1?+a12?f2?+?+a1p?fp?+ε1?,x2?=μ2?+a21?f1?+a22?f2?+?+a2p?fp?+ε2?,…xm?=μm?+am1?f1?+am2?f2?+?+amp?fp?+εm?,?
μ
=
(
μ
1
,
…
,
μ
m
)
T
\mu=(\mu_1,\dots,\mu_m)^T
μ=(μ1?,…,μm?)T 是
x
x
x 的期望变量,
f
=
(
f
1
,
…
,
f
p
)
T
f=(f_1,\dots,f_p)^T
f=(f1?,…,fp?)T 称公共因子向量,
ε
=
(
ε
1
,
…
,
ε
m
)
T
\varepsilon=(\varepsilon_1,\dots,\varepsilon_m)^T
ε=(ε1?,…,εm?)T 称特殊因子向量,
A
=
(
a
i
j
)
m
×
p
A=(a_{ij})_{m\times p}
A=(aij?)m×p? 称因子载荷矩阵,
a
i
j
a_{ij}
aij? 是变量
x
i
x_i
xi? 在公共因子
f
j
f_j
fj? 上的载荷,反映
f
j
f_j
fj? 对
x
i
x_i
xi? 的重要程度。
通常假设
f
j
f_j
fj?? 互不相关且具有单位方差,
ε
i
\varepsilon_i
εi?? 互不相关且与
f
j
f_j
fj???? 互不相关,
C
o
v
(
ε
)
=
ψ
Cov(\varepsilon)=\psi
Cov(ε)=ψ 为对角阵,于是有
C
o
v
(
x
)
=
A
A
T
+
ψ
,
C
o
v
(
x
,
f
)
=
A
.
Cov(x)=AA^T+\psi,Cov(x,f)=A.
Cov(x)=AAT+ψ,Cov(x,f)=A.
每个原始变量
x
i
x_i
xi? 的方差都可以分解成共性方差
h
i
2
h_i^2
hi2? 和特殊方差
σ
i
2
\sigma_i^2
σi2? 之和,其中
h
i
2
=
∑
j
=
1
p
a
i
j
2
h_i^2=\sum_{j=1}^pa_{ij}^2
hi2?=∑j=1p?aij2? 反映全部公共因子对
x
i
x_i
xi? 的方差贡献,
σ
i
2
=
D
(
ε
i
)
\sigma_i^2=D(\varepsilon_i)
σi2?=D(εi?)? 反映特殊因子的方差贡献。
令 b j 2 = ∑ i = 1 m a i j 2 b_j^2=\sum_{i=1}^ma_{ij}^2 bj2?=∑i=1m?aij2?,则 b j 2 b_j^2 bj2? 是公共因子 f j f_j fj?对 x x x 总方差的贡献,称 b j 2 ∑ i = 1 m ( h i 2 + σ i 2 ) \frac{b_j^2}{\sum_{i=1}^m(h_i^2+\sigma_i^2)} ∑i=1m?(hi2?+σi2?)bj2?? 为 f j f_j fj? 的贡献率。
利用主成分分析法求因子载荷矩阵,设
λ
1
≥
λ
2
≥
?
≥
λ
m
\lambda_1\ge\lambda_2\ge\dots\ge\lambda_m
λ1?≥λ2?≥?≥λm? 为相关系数矩阵
R
R
R 的特征值,
u
1
,
u
2
,
…
,
u
m
u_1,u_2,\dots,u_m
u1?,u2?,…,um? 为对应的正交特征向量,
p
<
m
p<m
p<m,则
A
=
(
λ
1
u
1
,
…
,
λ
p
u
p
)
,
A=(\sqrt{\lambda_1}u_1,\dots,\sqrt{\lambda_p}u_p),
A=(λ1??u1?,…,λp??up?),
特殊因子的方差用
R
?
A
A
T
R-AA^T
R?AAT 的对角元估计,即
σ
i
2
=
1
?
∑
j
=
1
p
a
i
j
2
.
\sigma_i^2=1-\sum_{j=1}^pa_{ij}^2.
σi2?=1?j=1∑p?aij2?.
一般来说,理想的载荷结构是,每一列或每一行各载荷平方接近 0 或 1,需要对因子载荷矩阵进行旋转。
选取方差最大的正交旋转矩阵
P
P
P??,使得因子上的载荷尽量拉开距离,从而使其接近 0 或 1
x
?
μ
=
(
A
P
)
(
P
T
f
)
+
ε
=
B
f
 ̄
+
ε
.
x-\mu=(AP)(P^Tf)+\varepsilon=B\overline{f}+\varepsilon.
x?μ=(AP)(PTf)+ε=Bf?+ε.
聚类分析
聚类分析,就是指将相似元素聚为一类。
层次聚类
基本思想:距离相近的样品先聚为一类,距离远的后聚成类,步骤如:
- 将每个样品独自聚成一类,构造 n n n 个类;
- 根据选定的距离公式,计算样品两两间距离,构造距离矩阵;
- 把距离最近的两类归为一类,聚成 n ? 1 n-1 n?1 类;
- 计算新类与当前各类的距离,再选距离最近的两类归为一类,聚成 n ? 2 n-2 n?2 类;
- 按步骤 4 重复迭代,直到所有样品聚为一类。
类和类之间的距离有各种定义,如最短距离法,对于类
G
i
,
G
j
G_i,G_j
Gi?,Gj??,有
D
i
j
=
min
?
w
s
∈
G
i
,
w
t
∈
G
j
d
s
t
.
D_{ij}=\min_{w_s\in G_i,w_t\in G_j}d_{st}.
Dij?=ws?∈Gi?,wt?∈Gj?min?dst?.
除此之外,还有最长距离法、中间距离法等。
K 均值聚类
动态聚类法的思想是先粗略分一下类,然后按某种最优原则进行修正,直到类分得较合理为止,K 均值法是动态聚类的一种方法。
假定样本可分为 C C C,并选定 C C C? 个初始聚类中心,然后根据最小距离原则将每个样本分配到某一类中,之后计算新的聚类中心,并调整聚类情况,直到收敛。
步骤如下:
-
将样本集任意划分为 C C C 类,记 G 1 , G 2 , … , G C G_1,G_2,\dots,G_C G1?,G2?,…,GC?,计算聚类中心 m 1 , m 2 , … , m C m_1,m_2,\dots,m_C m1?,m2?,…,mC?,
m i = 1 n i ∑ w j ∈ G i w j , i = 1 , 2 , … , C m_i=\frac{1}{n_i}\sum_{w_j\in G_i}w_j,i=1,2,\dots,C mi?=ni?1?wj?∈Gi?∑?wj?,i=1,2,…,C
其中 n i n_i ni? 为当前 G i G_i Gi? 类中的样本数,以及计算误差平方和
J e = ∑ i = 1 C ∑ w ∈ G i ∣ ∣ w ? m i ∣ ∣ 2 , J_e=\sum_{i=1}^C\sum_{w\in G_i}||w-m_i||^2, Je?=i=1∑C?w∈Gi?∑?∣∣w?mi?∣∣2, -
再令 G i = ? G_i=\varnothing Gi?=??,按最小距离原则重新聚类,并重新计算聚类中心;
-
若连续两次迭代 J e J_e Je? 不变,算法终止,否则转步骤 2。
最佳簇数 k 的确定
方法有簇内离差平方和拐点法和轮廓系数法。
- 簇内离差平方和拐点法
计算不同 k k k 值下计算簇内离差平方和,然后画图找到拐点。当斜率由大突然变小,且之后斜率变化缓慢,则认为突然变换的点就是寻找的目标点。 k k k 再增加聚类效果不再有大的变化。
- 轮廓系数法
思想为使簇内样本密集,簇间样本分散。
对于每个样本点 i i i? 有:
- 簇内不相似度 a ( i ) a(i) a(i)?:样本点 i i i? 与其所在簇内其他样本的平均距离;
- 簇间不相似度 b ( i ) b(i) b(i):样本点 i i i 与其他簇样本的平均距离的最小值。
于是有样本点
i
i
i? 的轮廓系数
S
i
=
b
i
?
a
i
max
?
{
a
i
,
b
i
}
.
S_i=\frac{b_i-a_i}{\max\{a_i,b_i\}}.
Si?=max{ai?,bi?}bi??ai??.
总轮廓系数为所有样本点轮廓系数的平均值。
总轮廓系数小于 0 说明聚类效果不佳;接近 1 说明簇内样本平均距离非常小,簇间最近距离非常大,聚类效果非常理想。
Python 代码
距离判别法
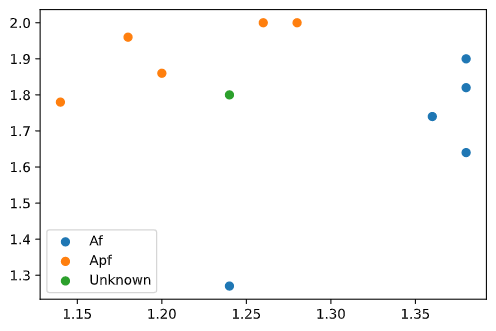
蠓虫分为 Af 和 Apf,测得 Af、Apf 的触角长度和翅膀长度数据。
Af: ( 1.24 , 1.27 ) (1.24,1.27) (1.24,1.27)?, ( 1.36 , 1.74 ) (1.36,1.74) (1.36,1.74)?, ( 1.38 , 1.64 ) (1.38,1.64) (1.38,1.64), ( 1.38 , 1.82 ) (1.38,1.82) (1.38,1.82), ( 1.38 , 1.90 ) (1.38,1.90) (1.38,1.90)?;
Apf: ( 1.14 , 1.78 ) (1.14,1.78) (1.14,1.78), ( 1.18 , 1.96 ) (1.18,1.96) (1.18,1.96), ( 1.20 , 1.86 ) (1.20,1.86) (1.20,1.86), ( 1.26 , 2.00 ) (1.26,2.00) (1.26,2.00), ( 1.28 , 2.00 ) (1.28,2.00) (1.28,2.00);
试判别 ( 1.24 , 1.80 ) (1.24,1.80) (1.24,1.80) 属于哪一类,代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-30
# @ function: 距离判别法
# %%
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
# %%
# 源数据
x0 = np.array([[1.24, 1.27],
[1.36, 1.74],
[1.38, 1.64],
[1.38, 1.82],
[1.38, 1.90],
[1.14, 1.78],
[1.18, 1.96],
[1.20, 1.86],
[1.26, 2.00],
[1.28, 2.00]])
# 前 5 个属于 1 类 af,后 5 个属于 2 类 apf
label = np.array([1 for i in range(5)] + [2 for i in range(5)])
# 待判别数据
x = np.array([[1.24, 1.80]])
# %%
# 画图
import matplotlib.pyplot as plt
plt.scatter(x0[:5,0], x0[:5,1],label='Af')
plt.scatter(x0[5:,0], x0[5:,1],label='Apf')
plt.scatter(x[0][0],x[0][1], label='Unknown')
plt.legend()
# %%
# 协方差矩阵
v = np.cov(x0.T)
# 模型
knn = KNeighborsClassifier(2,
metric='mahalanobis',
metric_params={'V': v})
knn.fit(x0, label)
knn.predict(x)
输出如下:
array([2])
从图中大致可以看出未知样本接近 Apf 类,而计算结果为 2,即 Apf 类,与直觉相吻合。
Fisher 判别法
对上例使用 Fisher 判别法求解,代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-30
# @ function: Fisher 判别法
# %%
import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# %%
# 源数据
x0 = np.array([[1.24, 1.27],
[1.36, 1.74],
[1.38, 1.64],
[1.38, 1.82],
[1.38, 1.90],
[1.14, 1.78],
[1.18, 1.96],
[1.20, 1.86],
[1.26, 2.00],
[1.28, 2.00]])
# 前 5 个属于 1 类 af,后 5 个属于 2 类 apf
label = np.array([1 for i in range(5)] + [2 for i in range(5)])
# 待判别数据
x = np.array([[1.24, 1.80]])
# %%
# 协方差矩阵
v = np.cov(x0.T)
# 模型
model = LinearDiscriminantAnalysis()
model.fit(x0, label)
model.predict(x)
输出如下:
array([2])
结果与距离判别法一致。
主成分分析
对下列数据进行主成分分析
| 序号 | 身高 x1 | 胸围 x2 | 体重 x3 |
|---|---|---|---|
| 1 | 149.5 | 69.5 | 38.5 |
| 2 | 162.5 | 77.0 | 55.5 |
| 3 | 162.7 | 78.5 | 50.8 |
| 4 | 162.2 | 87.5 | 65.5 |
| 5 | 156.5 | 74.5 | 49.0 |
代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-30
# @ function: 主成分分析
# %%
import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
# %%
# 源数据
df = pd.DataFrame({
'x1': [149.5, 162.5, 162.7, 162.2, 156.5],
'x2': [69.5, 77, 78.5, 87.5, 74.5],
'x3': [38.5, 55.5, 50.8, 65.5, 49]
})
# 模型
model = PCA().fit(np.array(df))
# %%
print('特征值:', model.explained_variance_)
print('贡献率:', model.explained_variance_ratio_)
print('各主成分的系数:', model.components_)
# %%
pca_df = pd.DataFrame(model.transform(np.array(df)))
pca_df.columns = ['F1', 'F2', 'F3']
pca_df
输出如下:
特征值: [161.47423448 9.60080441 2.28996111]
贡献率: [0.93141196 0.05537914 0.0132089 ]
各主成分的系数: [[-0.39412803 -0.5037512 -0.76869878]
[-0.90779807 0.34389304 0.24008381]
[ 0.14340765 0.79244703 -0.59284226]]
| F1 | F2 | F3 | |
|---|---|---|---|
| 0 | 17.867546 | 2.409312 | 0.343559 |
| 1 | -4.102132 | -2.731441 | -1.927107 |
| 2 | -1.323700 | -3.525555 | 2.076603 |
| 3 | -16.960269 | 3.552614 | 0.422142 |
| 4 | 4.518556 | 0.295070 | -0.915196 |
层次聚类
对下列 7 种岩石聚类
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| Cu | 2.9909 | 3.2044 | 2.8392 | 2.5315 | 2.5897 | 2.9600 | 3.1184 |
| W | 0.3111 | 0.5348 | 0.5696 | 0.4528 | 0.3010 | 3.0480 | 2.8395 |
| Mo | 0.5324 | 0.7718 | 0.7614 | 0.4893 | 0.2735 | 1.4997 | 1.9350 |
代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-30
# @ function: 层次聚类
# %%
import numpy as np
import pandas as pd
import scipy.cluster.hierarchy as sch
# %%
# 源数据
df = pd.DataFrame({
'Cu': [2.9909,3.2044,2.8392,2.5315,2.5897,2.9600,3.1184],
'W':[.3111,.5348,.5696,.4528,.3010,3.0480,2.8395],
'Mo': [.5324,.7718,.7614,.4893,.2735,1.4997,1.9350],
})
# 计算两两距离
dist = sch.distance.pdist(df)
# 转化为距离矩阵
dist_mat = sch.distance.squareform(dist)
# 聚类并画图
z = sch.linkage(dist)
sch.dendrogram(z)
输出如下:
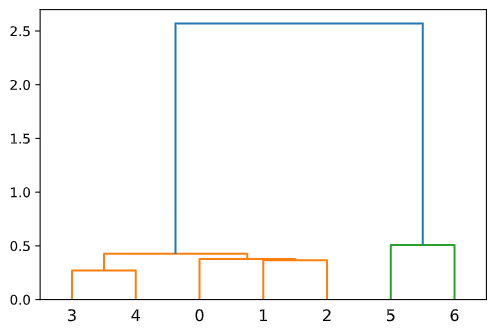
K 均值聚类
对鸢尾花数据集进行 K 均值聚类
| ID | sepal length (cm) | sepal width (cm) |
|---|---|---|
| 0 | 5.1 | 3.5 |
| 1 | 4.9 | 3.0 |
| 2 | 4.7 | 3.2 |
| 3 | 4.6 | 3.1 |
| 4 | 5.0 | 3.6 |
| … | … | … |
| 145 | 6.7 | 3.0 |
| 146 | 6.3 | 2.5 |
| 147 | 6.5 | 3.0 |
| 148 | 6.2 | 3.4 |
| 149 | 5.9 | 3.0 |
代码如下:
#! /usr/bin/env python
# -*- coding: utf-8 -*-
# @ author: Koorye
# @ date: 2021-7-30
# @ function: K 均值聚类
# %%
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# %%
# 源数据
df = pd.DataFrame(load_iris()['data'], columns=load_iris()['feature_names'])
# 计算 k 取不同值时的轮廓系数
score_list = []
for i in range(2,10):
model = KMeans(i)
model.fit(df.iloc[:,:2])
score_list.append(silhouette_score(df, model.labels_))
plt.plot([i for i in range(2,10)], score_list)
# %%
model = KMeans(3)
model.fit(df.iloc[:,:2])
df2 = df.iloc[:,:2].copy()
df2['label'] = model.labels_
from plotnine import *
(
ggplot(df2,aes('sepal length (cm)', 'sepal width (cm)', color='label'))
+ geom_point()
+ theme_matplotlib()
)
输出如下:
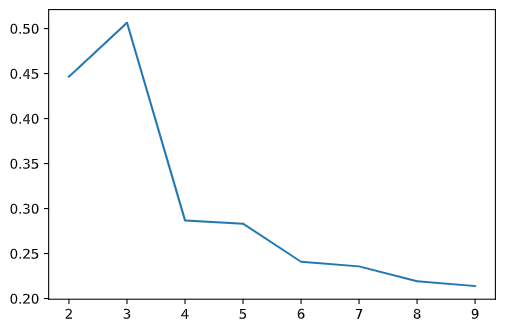
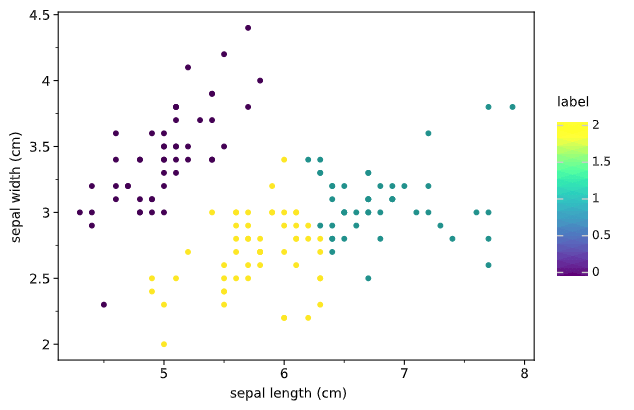
可以看到,分 3 类是轮廓系数最大,聚类效果如图。