写在前面

很遗憾，今天并没有取得什么实质性的进展，并且我还切实的感受到了误差函数发散的快感，今天这篇文章主要分享我的实现代码思路以及往期博客的一些纠正。

公式纠正

首先是对我上一篇博客中一个错误公式的纠正，错误公式如下图所示：

在这里插入图片描述
可以很明显的看到公式中出现了2个i的变量，昨天晚上脑子晕了，今天才发现，正确的公式应该如下图所示：

发散的误差函数

我的误差函数是均方根值：

在这里插入图片描述
我在程序里面的实现如下图所示：

det_Ek_v[i] = pow((y_out - y), 2) * 0.5

然后我设置了单张图片的训练，循环跑了50次，得到的结果居然是这个东西：

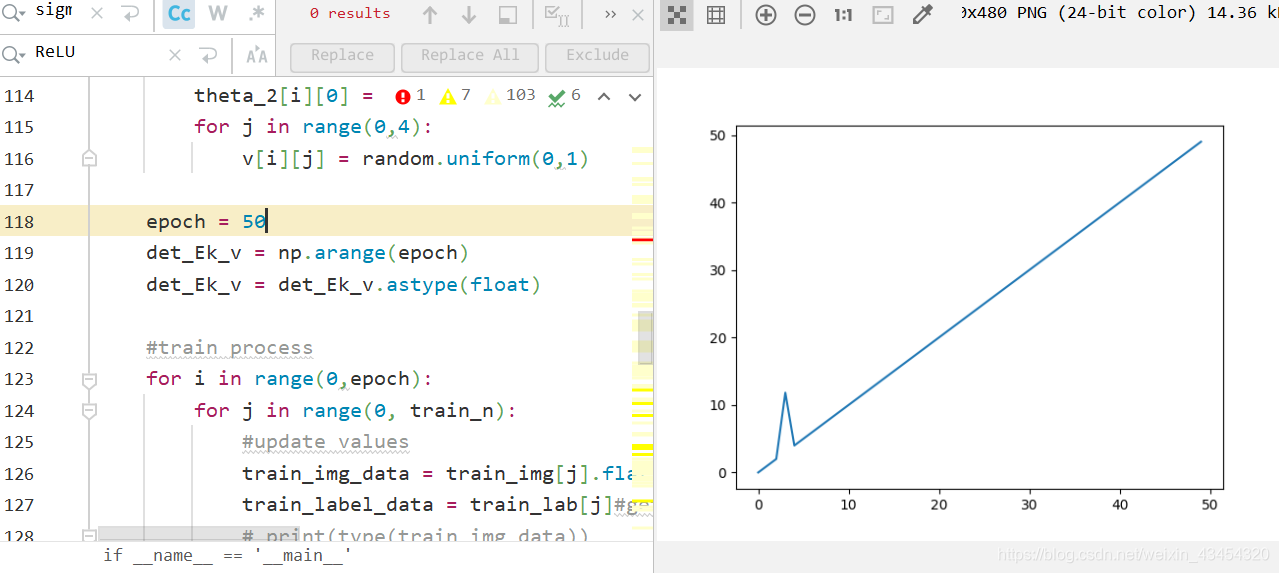
在这里插入图片描述
写这段程序只花了一下午，一时间就没有了调试的思路，先放出我的源码，明天接着调，脑袋疼。。

首先是激励函数了，我本来打算用的是sigmoid(x)，但是收敛情况实在是太不理想了，所以我改用了ReLU，结果还是没有变化，所以我感觉可能是我程序里的逻辑有问题，在这留下调试方向。

def ReLU(x):
    # s = 1 / (1 + np.exp(-x))
    if x > 0 :
        s = x
    else:
        s = 0
    return s

def ReLUDerivative(x):
    # ds = ReLU(x) * (1 - ReLU(x))
    if x > 0 :
        ds = 1
    else:
        ds = 0
    return ds

神经网络最重要的梯度数学公式我昨天已经给出了，今天做了python的实现。

            for i in range(0, 4):
                for j in range(0, 4):
                    v[i][j] =  (y_out - y) * (y_out * (1 - y_out)) * (n[j][0] * (1 - n[j][0])) * \
                              gamma[j][0] * m[i][0]
                    w[i][0] =  (y_out - y) * (y_out * (1 - y_out)) * gamma[j][0] * \
                              (n[i][0] * (1 - n[i][0])) * v[i][i] * (m[i][0] * (1 - m[i][0])) * x_sum + w[i][0]
                    theta_2[i][0] =  -1 * (y_out - y) * (y_out * (1 - y_out)) * gamma[i][0] * \
                                    (n[i][0] * (1 - n[i][0]))
                    theta_1[i][0] =  -1 * (y_out - y) * (y_out * (1 - y_out)) * gamma[j][0] * \
                                    (n[j][0] * (1 - n[j][0])) * v[i][j] * (m[i][0] * (1 - m[i][0])) + theta_1[i][0]
                    gamma[i][0] =  (y_out - y) * (y_out * (1 - y_out)) * n[i][0]
                    theta_3 = -1 *  (y_out - y) * (y_out * (1 - y_out))

            for i in range(0, 4):
                for j in range(0, 4):
                    v[i][j] = v[i][j] - study_step * v[i][j]
                    w[i][0] = w[i][0] - study_step * w[i][0]
                    theta_2[i][0] = w[i][0] - study_step * theta_2[i][0]
                    theta_1[i][0] = theta_1[i][0] - study_step * theta_1[i][0]
                    gamma[i][0] = gamma[i][0] - study_step * gamma[i][0]
                    theta_3 = theta_3 - study_step * theta_3

今天在做梯度公式实现的时候发现了一个问题，那就是虽然我只有一个单一的神经元，但是我在这个神经元里面输入了一个有784个数据的一维数组，导致我在处理隐层和输出层神经元的时候每个神经元都要对输入的数据做循环操作。而且我的最终输出神经网络输出也是一个一维的向量，因此我就把这个向量和输入向量做了一个对应位相减，然后把差值做累加求平均的做法，仔细一想这个方法是有问题的，因为这样做的话和我直接把输入的一维数组求均值输入是没有区别的，因此这个问题很有可能也是导致我的误差函数发散的原因。

下面这一段程序是我更新梯度的实现：

            for i in range(0,4):#[1,4]
                for j in range(0,784):
                    m[i][j] = x[j] * w[i][0] - theta_1[i];
                    m[i][j] = ReLU(m[i][j])

            # print(m)

            for i in range(0,4):#[1,4]
                for j in range(0,784):
                    n[i][j] = m[0][j] * v[0][i] + m[1][j] * v[1][i] + m[2][j] * v[2][i] + \
                              m[3][j] * v[3][i] - theta_1[i];
                    n[i][j] = ReLU(n[i][j])
            # print(n)

            for i in range(0, 784):
                y_arr[0][i] = n[0][i] * gamma[0][0] + n[1][i] * gamma[1][0] + n[2][i] * gamma[2][0] +\
                        n[3][i] * gamma[3][0] - theta_3;
                y_arr[0][i] = ReLU(y_arr[0][i])