1. 深层神经网络

??深层神经网络其实就是包含更多的隐藏层神经网络。
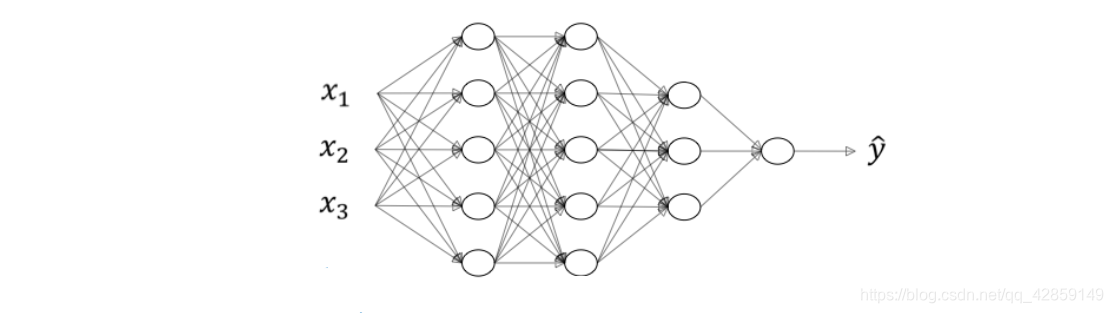
??如下图所示，分别列举了逻辑回归、1个隐藏层的神经网络、2个隐藏层的神经网络和5个隐藏层的神经网络它们的模型结构。
在这里插入图片描述
??命名规则上，一般只参考隐藏层个数和输出层。例如，上图中的逻辑回归又叫1 layer NN，1个隐藏层的神经网络叫做2 layer NN，2个隐藏层的神经网络叫做3 layer NN，以此类推。如果是L-layer NN，则包含了L-1个隐藏层，最后的L层是输出层。

??下面以一个4层神经网络为例来介绍关于神经网络的一些标记写法。如下图所示，首先，总层数用L表示， $L=4_{\circ}$ 输入层是第 0 层，输出层是第L层。 $n^{[l]}$ 表示第 $l$ 层包含的单元个数， $l=0,1，\cdots，L_{\circ}$ 这个模型中， $n^{[0]}=n_{x}=3$ ，表示三个输入特征 $x_{1}，x_{2}，x_{3 \circ} n^{[1]}=5$ ， $n^{[2]}=5，n^{[3]}=3，n^{[4]}=n^{[L]}=1_{\circ}$ 第l层的激活函数输出用 $a^{[l]}$ 表示， $a^{[l]}=g^{[l]}\left(z^{[l]}\right)_{\circ} W^{[l]}$ 表示第 $l$ 层的权重，用于计算 $z^{[l]}$ 。另外，我们把输入层记为 $a^{[0]}$ ，把输出层 $\hat{y}$ 记为 $a^{[L]}$ 。

??注意， $a^{[l]}$ 和 $W^{[l]}$ 中的上标 $l$ 都是从1开始的， $l=1，\cdots，L$ 。
在这里插入图片描述

2. 深层网络中的前向传播

??接下来，我们来推导一下深层神经网络的正向传播过程。仍以上面讲过的4层神经网络为例，对于单个样本：
在这里插入图片描述
??如果有m个训练样本，其向量化矩阵形式为：

??综上所述, 对于第 $l$ 层, 其正向传播过程的 $Z^{[l]}$ 和 $A^{[l]}$ 可以表示为:
$\begin{gathered} Z^{[l]}=W^{[l]} A^{[l-1]}+b^{[l]} \\ A^{[l]}=g^{[l]}\left(Z^{[l]}\right) \end{gathered}$ ??其中 $\cdots, L。$

3. 核对矩阵的维数

在这里插入图片描述

4. 为什么使用深层表示？

??在图像处理领域，深层神经网络随着层数由浅到深，神经网络提取的特征也是从边缘到局部特征到整体，由简单到复杂。如果隐藏层足够多，那么能够提取的特征就越丰富、越复杂，模型的准确率就会越高。

??在语音识别领域，浅层的神经元能够检测一些简单的音调，然后较深的神经元能够检测出基本的音素，更深的神经元就能够检测出单词信息。如果网络够深，还能对短语、句子进行检测。

??除了从提取特征复杂度的角度来说明深层网络的优势之外，深层网络还有另外一个优点，就是能够减少神经元个数，从而减少计算量。

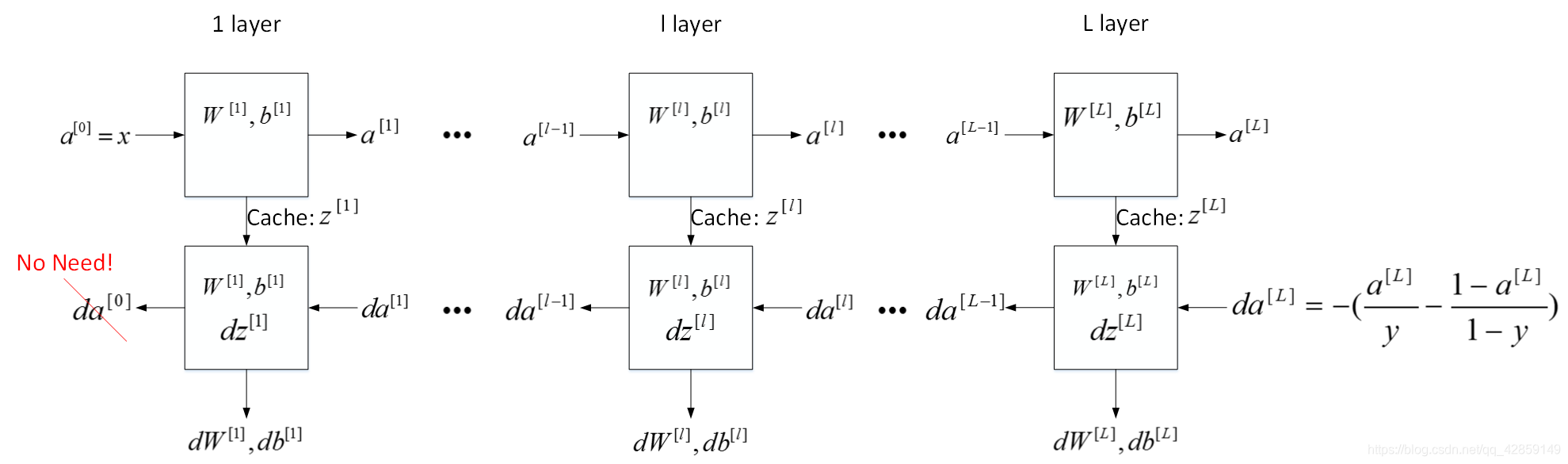
5. 前向传播和反向传播

前向传播：

输入： $a^{[l-1]}$
输出： $a^{[l]}$
缓存： $z^{[l]},w^{[l]},b^{[l]}$
$\begin{aligned} z^{[l]}&=W^{[l]} \cdot a^{[l-1]}+b^{[l]}\\ a^{[l]}&=g^{[l]}\left(z^{[l]}\right) \end{aligned}$
向量化写法
$\begin{aligned} Z^{[l]}&=W^{[l]} \cdot A^{[l-1]}+b^{[l]}\\ A^{[l]}&=g^{[l]}\left(Z^{[l]}\right) \end{aligned}$

后向传播：

输入: $d a^{[l]}$
输出: $d a^{[l-1]}, d w^{[l]}, d b^{[l]}$

??我们之前所用到的： $z^{[l]}=w^{[l+1] T} d z^{[l+1]} \cdot g^{[l]^{\prime}}\left(z^{[l]}\right)$ $\begin{aligned} d z^{[l]}&=d a^{[l]} * g^{[l]^{\prime}}\left(z^{[l]}\right) \\ d w^{[l]}&=d z^{[l]} \cdot a^{[l-1]} \\ d b^{[l]}&=d z^{[l]}\\ d a^{[l-1]}&=w^{[l] T} \cdot d z^{[l]} \end{aligned}$

向量化写法
$\begin{aligned} d Z^{[l]}&=d A^{[l]} * g^{[l]^{\prime}}\left(Z^{[l]}\right) \\ d W^{[l]}&=\frac{1}{m} d Z^{[l]} \cdot A^{[l-1] T}\\ d b^{[l]}&=\frac{1}{m} n p \cdot \operatorname{sum}\left(d Z^{[l]}\right., axis =1, keepdims = True )\\ d A^{[l-1]}&=W^{[l] T} \cdot d Z^{[l]} \end{aligned}$

6. 搭建神经网络块

在这里插入图片描述

7. 参数 vs. 超参数

??参数：模型可以根据数据可以自动学习出的变量，应该就是参数。比如，深度学习的权重w，偏差b等。
??超参数：就是用来确定模型的一些参数，超参数不同，模型是不同的，超参数一般就是根据经验确定的变量。在深度学习中，超参数有：学习速率，梯度下降的迭代次数，隐藏层数量，隐藏层单元数量以及激活函数选择等等。

进行多种组合，各种尝试，目的是选择效果最好的参数组合，在第二门课会介绍具体方式。