[人工智能]径向基和径向基神经网路

一、问题背景

许多物理和工程实际问题都可以用偏微分方程来描述，但是只有极少数的偏微分方程可以得到精确解，所以对于一般的偏微分方程，都是借助于数值方法求解．比较成熟的数值方法中大部分是依赖于网格的，如有限差分法、有限元法、有限体积等等．这些方法必须先生成网格后才能求解，网格质量的好坏直接决定了最终数值求解的精度，而网格生成的预处理耗费时间太大，在求解区域不规则或维数较高时，这些方法都有一定的困难．另一方面，在应用这些方法求解大变形、断裂问题或高维问题，特别是非定常问题，很多时候在求解的过程中都需要网格重构，这大大地增加了计算量，也严重降低了数值解的精度. 为了解决有限元方法等对网格依赖的问题，无网格方法近年来受到了很大的关注．这类方法试图彻底地或部分地消除网格．相对于网格依赖的数值方法，无网格方法具有一些明显的优点，因此在其出现后得到了日益众多的关注，并且一直是偏微分方程数值方法中的一个研究热点．一般说来，无网格方法基于一系列节点进行函数插值，与有限元等网格依赖的方法相比，避免了网格划分的预处理过程，也不会出现网格畸变的问题，对间断问题、解的变化较大的问题等具有较好的优势．另一方面，无网格方法只需各个节点的独立信息，而不需要单元之间的相互信息，数据结构简单．

二、径向基概念

利用径向基函数 (Radial Basis Function, RBF) 求解偏微分方程的方法，是最近十年来备受关注的一类无网格方法。其基本思想是在求解区域内根据所求解的问题布置节点，然后在每个节点上构造 RBF，再将 RBF 代入到所求解的偏微分程，通过求解最终得到的代数方程获得近似解．与网格依赖的方法不同， RBF 方法不需要任何网格，对支撑域和边界没有要求，只需要以节点为中心的子域覆盖所求解区域即可．同时， RBF 与空间维数无关，仅依赖于节点间的距离，低维结果可以很容易推广到高维问题．

1、径向基函数及其导数

2、利用径向基求解偏微分方程的步骤

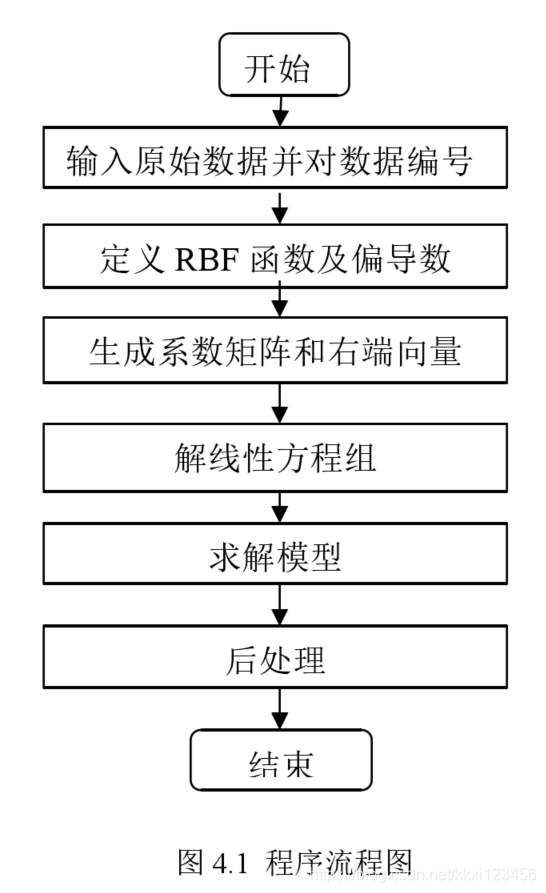
3、径向基的缺点

RBF 方法的缺点也是显而易见的，如理论方面很不完善，在逼近过程中所得到矩阵方程的系数矩阵是否可逆没有相关理论结果，也即数值解的唯一性还没解决；随着中心节点增加，需要求解一个很大的方程组，并且这个方程组经常是病态的；尚未见到开源或商业化的软件，后处理以及所得结果与其他软件的接口比较困难等等．

三、径向基神经网络

参考：
径向基函数神经网络（RBFNN）详解
深度学习 — 径向基神经网络RBF详解
RBF神经网络即径向基函数网络(Radial Bisis Function Network)，是一种使用径
向基函数作为激活函数的人工神经网络 。 如下图所示，神经网络是一种三层前向网络。

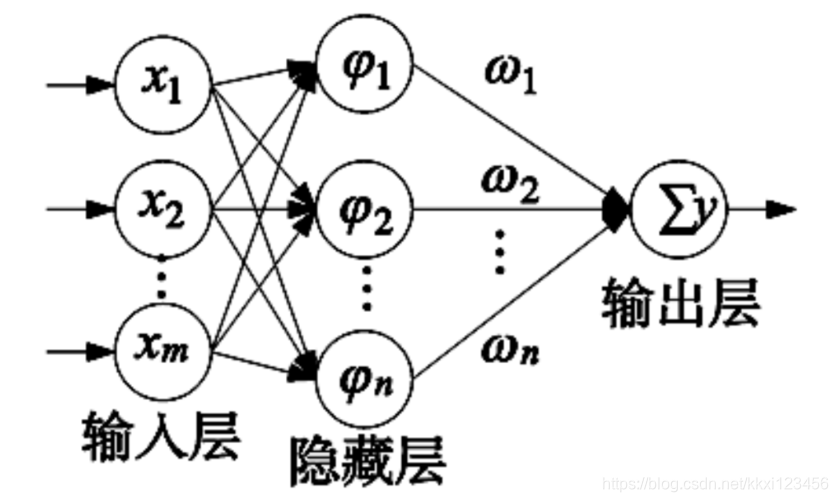
第一层为输入层，由信号源结点组成；第二层为隐含层，以径向基函数为隐含层各单元的变换函数，输入层到隐含层为衰减的非负非线性函数，即 ＲＢＦ 神经网络隐含层的功能是将低维输入通过非线性函数映射到一个高维空间。 然后在这个高维空间进行曲线的拟合；第三层为输出层，对输入信号作出响应，隐含层到输出则是线性变换的函数，即隐含层的信号通过线性的加权求值得到输出层的输出值，其中权值为可调参数 $w_{ij}$.



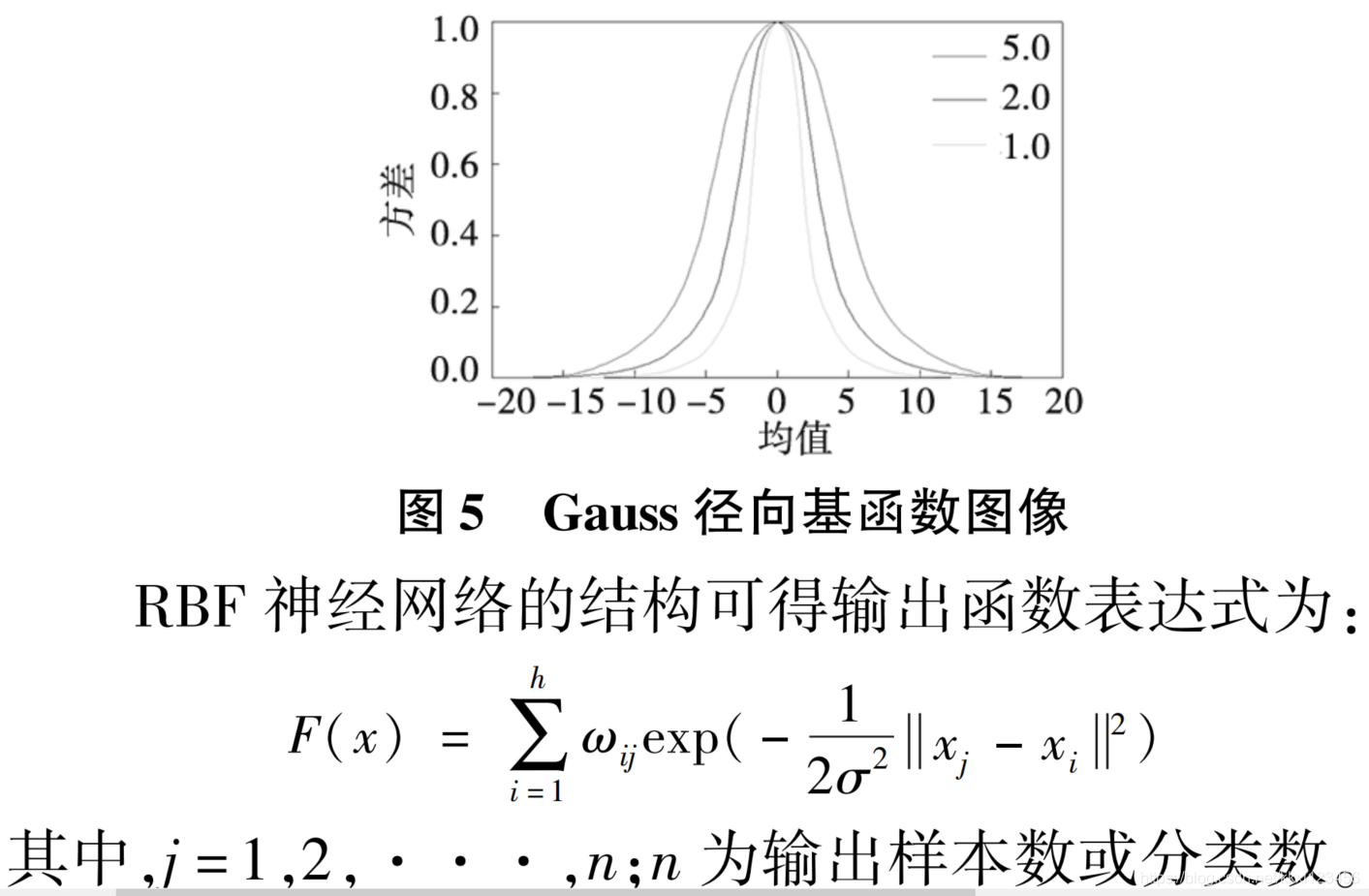
python代码

from scipy.linalg import norm, pinv
from matplotlib import pyplot as plt
from math import *
from numpy import *

class RBF:
    def __init__(self, indim, numCenters, outdim):
        self.indim = indim
        self.outdim = outdim
        self.numCenters = numCenters
        self.centers = [random.uniform(-1, 1, indim) for i in range(numCenters)]
        self.beta = 8
        self.W = random.random((self.numCenters, self.outdim))

    def _basisfunc(self, c, d):
        assert len(d) == self.indim
        return exp(-self.beta * norm(c-d)**2)

    # enumerate多用于在for循环中得到计数，利用它可以同时获得索引和值，即需要index和value值的时候可以使用enumerate
    def _calcAct(self, X):
        # calculate activations of RBFs
        G = zeros((X.shape[0], self.numCenters), float)
        for ci, c in enumerate(self.centers):
            # ci是索引, c是索引对应的值
            for xi, x in enumerate(X):
                # xi是索引, x是索引对应的值
                G[xi, ci] = self._basisfunc(c, x)
        return G

    def train(self, X, Y):
        """ X: matrix of dimensions n x indim
            y: column vector of dimension n x 1 """

        # choose random center vectors from training set, 从训练集中选取部分元素作为centroid
        rnd_idx = random.permutation(X.shape[0])[:self.numCenters]
        self.centers = [X[i, :] for i in rnd_idx]
        print("center", self.centers)

        # calculate activations of RBFs
        G = self._calcAct(X)
        print("G:", G)

        # calculate output weights (using pseudo—inverse)
        self.W = dot(pinv(G), Y)

    def test(self, X):
        """ X: matrix of dimensions n x indim """

        G = self._calcAct(X)
        Y = dot(G, self.W)
        return Y


if __name__ == '__main__':
    n = 200
    x = mgrid[-2:2:complex(0, n)].reshape(n, 1)
    y = x**3

    # rbf regression
    rbf = RBF(1, 25, 1)
    rbf.train(x, y)
    z = rbf.test(x)

    # plot original data
    plt.figure(figsize=(12, 8))
    plt.plot(x, y, 'r-')

    # plot learned model
    plt.plot(x, z, 'b-', linewidth=2)

    # plot rbfs
    plt.show()

参考文献:
基于径向基函数的自适应网格方法，段献葆, 党 妍, 秦 玲， 西安理工大学理学院
地下水污染模拟的时空径向基配法研究，樊田田，辽宁师范大学
基于RBF神经网络的六自由度机械臂轨迹优化，柘龙炫，李少波，张星星，宋启松，贵州大学机械工程学院