[人工智能]【温大机器学习笔记】-朴素贝叶斯

朴素贝叶斯（Native Bayes）

法如其名，它是贝叶斯分类中，最简单也是最常见的分类算法。
它是以贝叶斯定理为基础
通常要理解这么几个概念
**先验概率：**根据以往经验和分析得到的概率，$P(Y)$
**后验概率：**根据已发生的事件来分析得到的概率,$P(Y|X)$
**联合概率：**联合概率是在多元的概率分布中，多个随机变量分别满足各自条件的概率，数学符号：$$P(X,Y)、P(XY)、P(X\cap Y)$$也就是事件A和B同时发生的概率
举个例子：

我对一个陌生的朋友判断是否为好人
老子说：人之初性本善，那么我觉得他99%是好人，1%是坏人-先验概率
有一天，因为我没有去上课，结果他给任课老师把我举报了！
真坏！
这是我觉得他50%是好人，50%是坏人。-后验概率
黄老师给的公式：

朴素贝叶斯原理

判别模型和生成模型
监督学习分为生成方法（Generative approach）和判别方法（discriminative approach）
所学到的模型分别是
监督学习分为生成模型（Generative Model）和判别模型（discriminative Model）

朴素贝叶斯是典型的生成学习方法
生成方法由训练数据学习联合概率分布$P(X,Y)$，然后求得后验概率分布$P(Y|X)$，即是求
$$P(X,Y)=P(Y)P(X|Y)$$
最重要的假设：相互独立-所以叫native

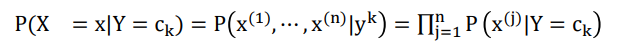
$C_k$表示类别，k表示类别个数
如果给定Z的情况下，X和Y条件独立：
$$P(X|Z)=P(X|Y,Z)$$
也可以表示为
$$P(X,Y|Z)=P(X|Z)P(Y|Z)$$

根据极大似然函数


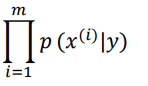
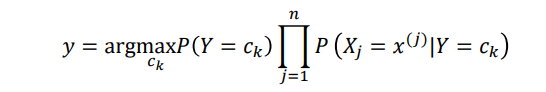
这里后验概率最大等价于0-1损失函数期望风险最小
推导过程：
根据贝叶斯定理

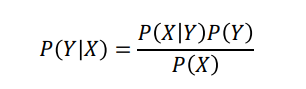
计算起后验概率

将式1带入式2

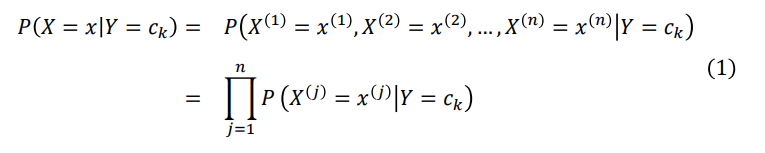
实际案例

这个案例不好理解！
推荐一个好理解的【案例传送门】

代码实现

贝叶斯分类器
GaussianNB高斯贝叶斯分类器，最常见，满足高斯分布

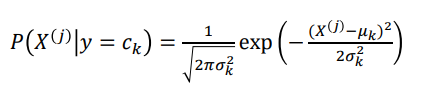
MultinomialNB多项贝叶斯分类器，条件概率分布满足多项式分布
BernoulliNB伯努利贝叶斯分类器，条件概率满足二项分布

基于scikit-learn的实现

import numpy as np

X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
y = np.array([1,1,1,2,2,2])
# 引入高斯朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
# 实例化
clf = GaussianNB()
# 训练数据
clf.fit(X,y)
# 输入单个预测结果
print('-----predict result by predict-----')
print(clf.predict([[-0.8,-1]]))
print('-----predict result by predict_proba-----')
print(clf.predict_proba([[-0.8,-1]]))
print('-----predict result by predict_log_proba-----')
print(clf.predict_log_proba([[-0.8,-1]]))

输出结果:

-----predict result by predict-----
[1]
-----predict result by predict_proba-----
[[9.99999949e-01 5.05653254e-08]]
-----predict result by predict_log_proba-----
[[-5.05653266e-08 -1.67999998e+01]]

基于自写GaussianNB的高斯朴素贝叶斯numpy实现

import numpy as np
from sklearn import datasets

# 加载数据
iris = datasets.load_iris()

X = np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
y = np.array([1,1,1,2,2,2])
# 引入高斯朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
# 实例化
clf = GaussianNB()
# 训练数据
clf.fit(X,y)
# 输入单个预测结果
print('-----predict result by predict-----')
print(clf.predict([[-0.8,-1]]))
print('-----predict result by predict_proba-----')
print(clf.predict_proba([[-0.8,-1]]))
print('-----predict result by predict_log_proba-----')
print(clf.predict_log_proba([[-0.8,-1]]))

# 基于GaussianNB的朴素贝叶斯numpy实现

# 先定义一个类
class NaiveBayes:

    def __init__(self):
        print('Gaussian naive bayes model!')

    def gaussian_pdf(self,x_test,x):

        """
        计算高斯正态分布下的条件概率
        params:
            x_test(array):
            x(array):同属于一个类别
        """
        temp1 = (x_test-x.mean(0))*(x_test-x.mean(0))
        temp2 = x.std(0) * x.std(0)

        return np.exp(-temp1 / (2 * temp2)) / np.sqrt(2 * np.pi * temp2)

    def fit(self,x_train,y_train):
        self.x_train = x_train
        self.y_train = y_train

    def predict(self,x_test,y_test=None):
        assert len(x_test.shape) == 2
        # 这里应该是y_test
        self.classes = np.unique(np.concatenate([x_test,y_test],0))
        pred_probs = []

        # 对于每一个输入，计算器处于每个类别的概率
        for i in self.classes:
            idx_i = self.y_train == i
            # 计算P(y)
            p_y= len(idx_i) / len(self.y_train)

            # 利用高斯概率密度函数计算P(x|y)

            p_x_y = np.prod(self.gaussian_pdf(x_test,self.x_train[idx_i]),1)

            # 计算x,y的联合概率，P(x|y)P(y)
            prob_i = p_y * p_x_y

            pred_probs.append(prob_i)
        pred_probs = np.vstack(pred_probs)

        # 去具有最高概率的类别
        label_idx = pred_probs.argmax(0)
        y_pred = self.classes[label_idx]
        if y_test is not None:
            self._score(y_test,y_pred)
        return y_pred

    def _score(self,y_test,y_pred):
        self.score = np.count_nonzero(y_test == y_pred)/len(y_test)





model = NaiveBayes()
model.fit(iris.data, iris.target)
print('GaussianNB train done!')
print(model.predict(np.array([4.4,3.2,1.3,0.2])))
#print(model.score(X,y))