前言
为 西电数模培训《机器学习》-最小二乘法作业
1. warm start

固定了 θ \theta θ,研究 γ \gamma γ取值变化时等值线的变化规律
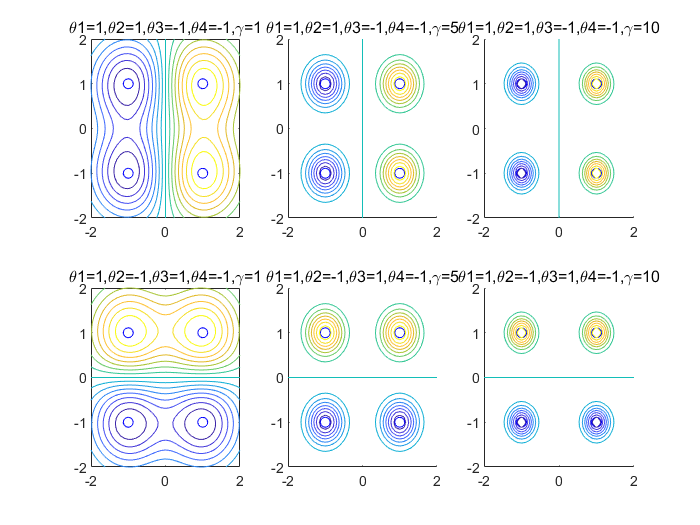
可以看出,对应 θ \theta θ同号的点附近的取值更接近,在图1,2,3中,(1,1)和(1,-1)对应 θ \theta θ同号,另外两个同号,则等高线明显分成左右两部分,在图4,5,6中,则明显分成上下两部分。且随着 γ \gamma γ增大,等高线越向取定的四个点靠近。
代码如下:
x=[1,1;1,-1;-1,1;-1,-1]'
X=-2:0.1:2
Y=X
N=length(X)
[X,Y]=meshgrid(X,Y)
for i =1:N
for j=1:N
Z1(i,j)=norm([X(i,j),Y(i,j)]-[1,1])^2
Z2(i,j)=norm([X(i,j),Y(i,j)]-[1,-1])^2
Z3(i,j)=norm([X(i,j),Y(i,j)]-[-1,1])^2
Z4(i,j)=norm([X(i,j),Y(i,j)]-[-1,-1])^2
end
end
%相邻两点对应的theta同号,theta用t表示,gamma=1,用g表示
t1=1;t2=1;t3=-1;t4=-1,g=[1,5,10]
f=t1*exp(-g(1)*Z1)+t2*exp(-g(1)*Z2)+t3*exp(-g(1)*Z3)+t4*exp(-g(1)*Z4)
subplot(2,3,1);plot(x(1,:),x(2,:),'bo');
hold on
contour(X,Y,f,15)
title('\theta1=1,\theta2=1,\theta3=-1,\theta4=-1,\gamma=1')
f=t1*exp(-g(2)*Z1)+t2*exp(-g(2)*Z2)+t3*exp(-g(2)*Z3)+t4*exp(-g(2)*Z4)
subplot(2,3,2);hold on;plot(x(1,:),x(2,:),'bo');contour(X,Y,f,15)
title('\theta1=1,\theta2=1,\theta3=-1,\theta4=-1,\gamma=5')
f=t1*exp(-g(3)*Z1)+t2*exp(-g(3)*Z2)+t3*exp(-g(3)*Z3)+t4*exp(-g(3)*Z4)
subplot(2,3,3);hold on;plot(x(1,:),x(2,:),'bo');contour(X,Y,f,15)
title('\theta1=1,\theta2=1,\theta3=-1,\theta4=-1,\gamma=10')
%相邻两点对应theta异号
t1=1;t2=-1;t3=1;t4=-1,g=[1,5,10]
f=t1*exp(-g(1)*Z1)+t2*exp(-g(1)*Z2)+t3*exp(-g(1)*Z3)+t4*exp(-g(1)*Z4)
subplot(2,3,4);plot(x(1,:),x(2,:),'bo');
hold on
contour(X,Y,f,15)
title('\theta1=1,\theta2=-1,\theta3=1,\theta4=-1,\gamma=1')
f=t1*exp(-g(2)*Z1)+t2*exp(-g(2)*Z2)+t3*exp(-g(2)*Z3)+t4*exp(-g(2)*Z4)
subplot(2,3,5);hold on;plot(x(1,:),x(2,:),'bo');contour(X,Y,f,15)
title('\theta1=1,\theta2=-1,\theta3=1,\theta4=-1,\gamma=5')
f=t1*exp(-g(3)*Z1)+t2*exp(-g(3)*Z2)+t3*exp(-g(3)*Z3)+t4*exp(-g(3)*Z4)
subplot(2,3,6);hold on;plot(x(1,:),x(2,:),'bo');contour(X,Y,f,15)
title('\theta1=1,\theta2=-1,\theta3=1,\theta4=-1,\gamma=10')
2.分类器
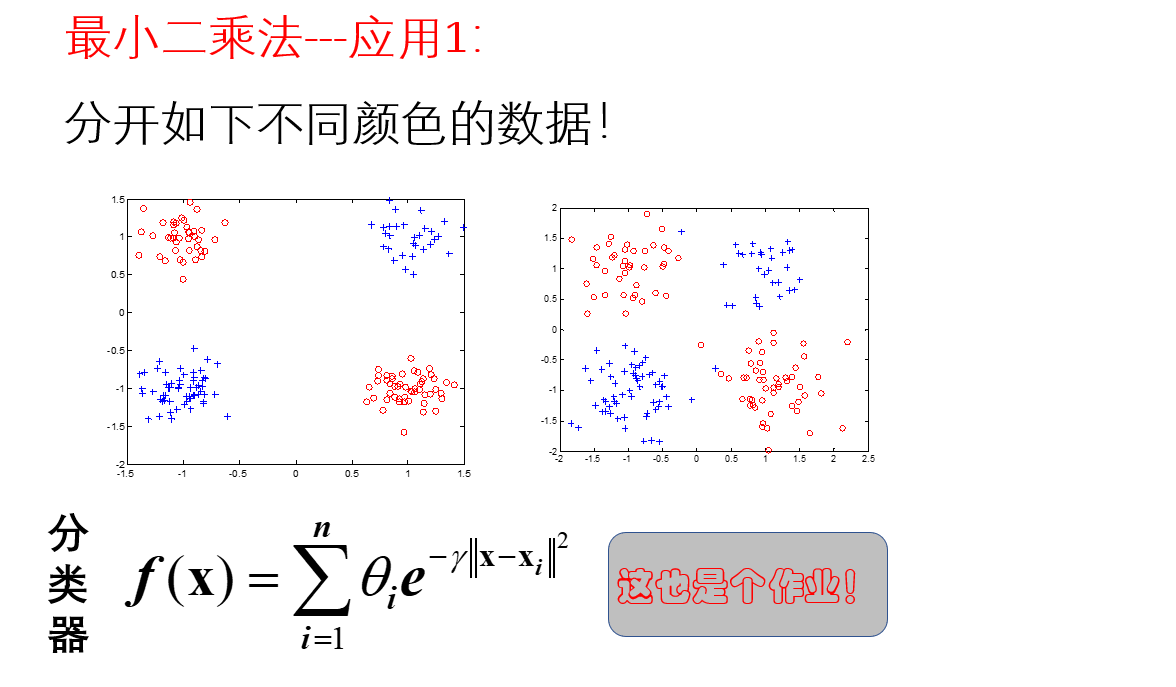
取定(1,1),(1,-1),(-1,-1),(-1,1)四个点,其他点用二维高斯分部生成。由(1,1),(-1,-1)生成的点处f(x)取值1,其他取值-1,便可构成分类器
代码如下:
%服从二维高斯分布
clear;clf
mu = [1 1];
SIGMA = [0.1 0; 0 0.1];
r = mvnrnd(mu,SIGMA,20);
plot(r(:,1),r(:,2),'r+');
hold on;
mu = [1 -1];
SIGMA = [ 0.1 0; 0 0.1];
r2 = mvnrnd(mu,SIGMA,20);
plot(r2(:,1),r2(:,2),'b*')
mu = [-1 -1];
SIGMA = [ 0.1 0; 0 0.1];
r3 = mvnrnd(mu,SIGMA,20);
plot(r3(:,1),r3(:,2),'r+')
mu = [-1 1];
SIGMA = [ 0.1 0; 0 0.1];
r4 = mvnrnd(mu,SIGMA,20);
plot(r4(:,1),r4(:,2),'b*')
%分类
x1=[r(:,1);r2(:,1);r3(:,1);r4(:,1)]
x2=[r(:,2);r2(:,2);r3(:,2);r4(:,2)]
y1=ones(20,1)
y2=-1*y1
y=[y1;y2;y1;y2]
x=[x1,x2]-[1,1]
w=x.^2
e=w(:,1)+w(:,2)
fun=@(x)x(1)*exp(-x(5)*e)...
+x(2)*exp(-x(5)*e)...
+x(3)*exp(-x(5)*e)...
+x(4)*exp(-x(5)*e)-y
x0=[-1,-1,-1,-1,1]
[x,resnorm,residual,exitflag,output] = lsqnonlin(fun,x0,[],[])
%得到x的值,即为各'\theta'和gamma的最优解,resnorm为残差平方和,residual即为在最优解处的目标函数值
得到的结果如图
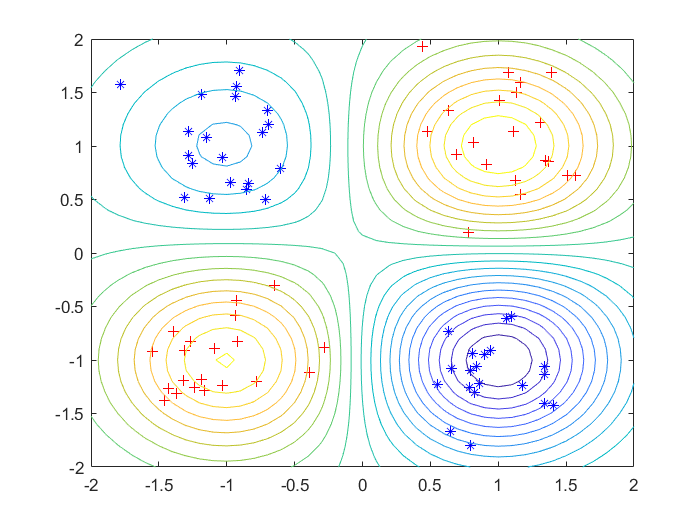
3.矩阵完备化

原来的矩阵A,B是一个m*r,C为 r * n,r<<m,n,就可以保证rank(A)<r,即A低秩
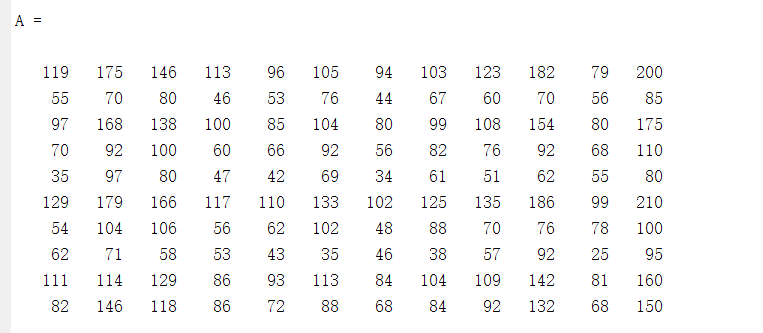
随机去值后的Ap
恢复的矩阵Abar:
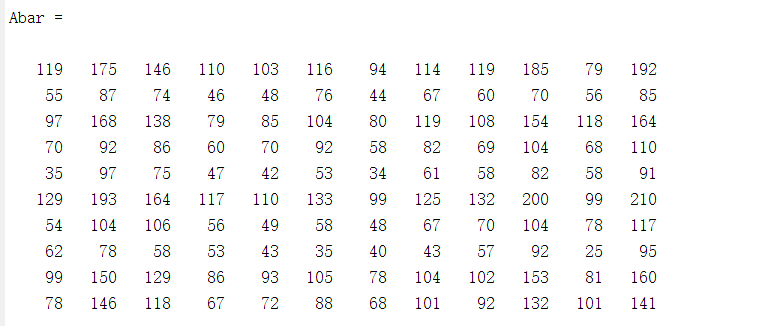
代码如下:
%生成不完备矩阵
m=10;n=12
r=3;p=70%剩余个数
B=randi(10,m,r);C=randi(10,r,n)
A=B*C
b=rank(A)
a=A(:);S
I=randperm(length(a));a(I(p+1:end))=inf
Abar=reshape(a,m,n)
Ap=Abar
%恢复代码
% A为mxn,B为mxr, C为rxn
r =3; % 猜测r
x0 = randi(10,m+n,r);
% 非线性最小二乘法
fun = @(x)fmatrix( x, m , n ,Abar);
x = lsqnonlin(fun,x0);
AbarRecover =round( x(1:m ,:) * x(m+1:n+m ,:)')
Abar(Abar == Inf) = AbarRecover(Abar == Inf)
function y = fmatrix(x, m , n , Abar)
y = Abar - x(1:m ,:) * x(m+1:n+m ,:)';
y(y == inf) = 0;
end
4.灰度图像恢复

选择图像

恢复图像

代码:
clear,clc;
A = double( imread('rc.jpg'));
A = A(:,:,2);
imshow(A,[0,255])
disp('原图秩:')
rank(A)
[m , n] = size(A);
p = 200000;
a = A(:);
I = randperm(length(a));
a(I(p+1:end)) = inf;
A = reshape(a,m,n);
imshow(A,[0,255]);
% A为mxn,B为mxr, C为rxn
r = 10; % 猜测r
x0 = randi(16,m+n,r);
% 非线性最小二乘法
fun = @(x)f_matrix( x, m , n ,A);
x = lsqnonlin(fun,x0);
ARecover = round( x(1:m ,:) * x(m+1:n+m ,:)');
A(A == Inf) = ARecover(A == Inf);
imshow(ARecover,[0,255])
imshow(A,[0,255])
function y = f_matrix(x, m , n ,Abar)
y = Abar - x(1:m ,:) * x(m+1:n+m ,:)';
y(y == inf) = 0;
end