1.梯度下降的方式
| 区别 | 梯度下降 | 随机梯度下降(SGD) |
|---|---|---|
| 特点 | 一大块数据一起操作 | 小块数据分开操作 |
| 性能(越高越好) | 低 | 高 |
| 时间复杂度(越低越好) | 低 | 高 |
2.朴素梯度下降
# -*- coding:utf-8 -8-
"""
Author: Leung
Date: 2021--08--01
"""
import matplotlib.pyplot as plt
import numpy as np
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1 # 初始化
a = 0.01 # 学习速率
def forward(x):
return w * x
def cost(xs, ys):
cost_sum = 0
assert (len(xs) == len(ys)); # 确定长度相等
for x_val, y_val in zip(xs, ys):
y_pred = forward(x_val)
cost_sum += (y_pred - y_val) * (y_pred - y_val)
return cost_sum / len(ys)
def back_prog(xs, ys):
sum_grad = 0
assert (len(xs) == len(ys))
for x_val, y_val in zip(xs, ys):
y_pred = forward(x_val)
sum_grad += 2 * x_val * (y_pred - y_val)
delta_w = a * sum_grad / len(ys)
return delta_w
print("Gradient decent begins...")
cost_vector = []
w_vector = []
for epoch in range(100):
w_vector.append(w)
# 计算此时的损失函数
cost_val = cost(x_data, y_data)
cost_vector.append(cost_val)
# 更新w
delta_w = back_prog(x_data, y_data)
w = w - delta_w
print("\t 第", epoch, "次迭代 ", " cost_val = ", cost_val);
x_ax = np.arange(1,101)
# print(x_ax[0])
plt.plot(x_ax, cost_vector)
plt.xlabel("epoch")
plt.ylabel('value_y')
plt.show()
print("the final w: ",w_vector[len(w_vector)-1])
运行结果
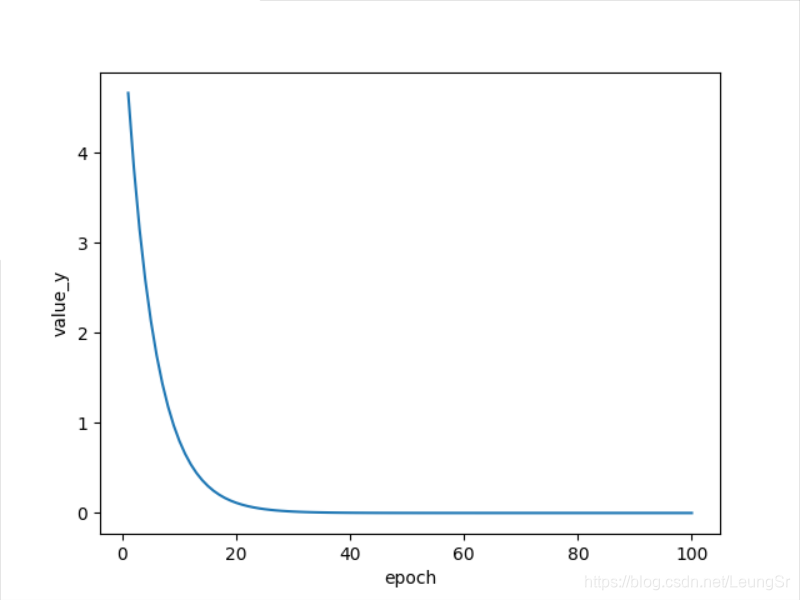
3.随机梯度下降(SGD)
随机梯度下降(Stochastic Gradient Decent)可以在下降的过程中随机地加入一些白噪声,使得我们的在遇到鞍点的情况下仍然能够继续迭代前进(鞍点处的梯度为零,可以类比于 y = x 3 , x = 0 y=x^3,x=0 y=x3,x=0处的导数)
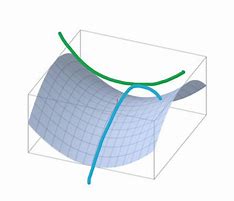
上图为鞍点示意图
# -*- coding:utf-8 -8-
"""
Author: Leung
Date: 2021--08--01
"""
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1 # 初始化
a = 0.01 # 学习速率
def forward(x):
return w * x
def loss(xs, ys):
y_pred = forward(xs)
return (y_pred - ys) * (y_pred - ys)
def grad(xs, ys):
y_pred = forward(xs)
return 2 * xs * (y_pred - ys)
loss_vector =[]
for loop in range(100):
for x_val,y_val in zip(x_data,y_data):
loss_vector.append(loss(x_val,y_val))
w = w-a*grad(x_val,y_val)
x_vector = np.arange(1,301)
plt.plot(x_vector,loss_vector)
plt.show()
运行结果
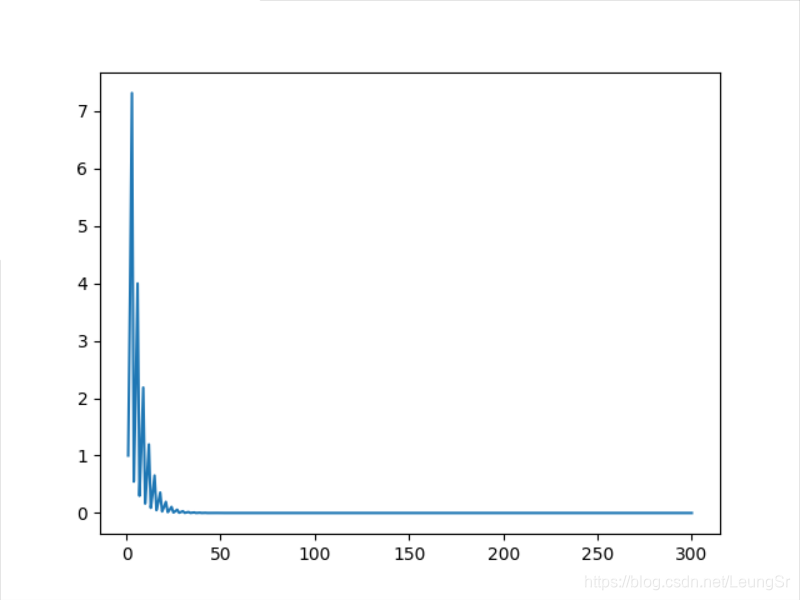
写在最后
本文章为《PyTorch深度学习实践》完结合集课程对应的一些课后习题解答,仅为各位同志学习参考之用
各位看官,都看到这里了,麻烦动动手指头给博主来个点赞8,您的支持作者最大的创作动力哟! <(^-^)>
才疏学浅,若有纰漏,恳请斧正
本文章仅用于各位同志作为学习交流之用,不作任何商业用途,若涉及版权问题请速与作者联系,望悉知