文章目录
1. 基本概念
1.1 集成学习概述
之前我有总结过分类树,回归树的基本流程和分类树类似,不过属性划分的原则存在一点差异,对于连续属性而言,考虑的是划分子区域的方差:
意思就是通过阈值1基于属性1进行划分成两个子集,两个子集内方差越小越好,最终回归预测结果为每个子树预测结果求均值。
集成学习(Esemble Learning)的思想就是构建并结合多个学习器完成学习任务:
{
学
习
器
1
:
f
1
(
X
)
学
习
器
2
:
f
2
(
X
)
.
.
.
学
习
器
n
:
f
n
(
X
)
}
结
合
多
个
学
习
器
\begin{Bmatrix} 学习器1: & f_1(X) \\ 学习器2: & f_2(X)\\ ...\\ 学习器n: & f_n(X) \end{Bmatrix}结合多个学习器
????????学习器1:学习器2:...学习器n:?f1?(X)f2?(X)fn?(X)?????????结合多个学习器
对这种集成的策略做一个总结,集成学习(Esemble Learning)分为三种:
- Bagging:bootstrap aggregating的缩写,bootstrap也称为自助法,它是一种有放回的抽样方法,在Bagging方法中,利用bootstrap方法从整体数据集中采取有放回抽样得到N个数据集,在每个数据集上学习出一个模型,最后的预测结果利用N个模型的输出得到,具体地:分类问题采用N个模型预测投票的方式,回归问题采用N个模型预测平均的方式。比较典型的就是随机森林;
- Boosting:提升方法(Boosting)是一种可以用来减小监督学习中偏差的机器学习算法。主要也是学习一系列弱分类器,并将其组合为一个强分类器。比较典型的是Adaboost、GBDT、XGBoost;
- Stacking:Stacking方法是指训练一个模型用于组合其他各个模型。首先我们先训练多个不同的模型,然后把之前训练的各个模型的输出为输入来训练一个模型,以得到一个最终的输出。理论上,Stacking可以表示上面提到的两种Ensemble方法,只要我们采用合适的模型组合策略即可。但在实际中,我们通常使用logistic回归作为组合策略。
1.2 Boosting相关算法
这一小节就概述一下Boosting相关模型,总结不到位,欢迎大佬们批评指正,多多交流。
Boosting的基本思想是用下一个学习器拟合上一个学习器的残差:
初始学习器输入为特征 X X X,预测目标是真实值 Y Y Y,对于下一个学习器,其预测目标则为上一个学习器学习得到的残差: y ^ ? y \hat y-y y^??y。
1.2.2 BDT
BDT(Boosting Decision Tree)的核心思想如下:
- 加法模型:提升树中M个树的和 f M ( x ) = ∑ m = 1 M T ( x , θ m ) f_M(x)=\sum_{m=1}^{M}T(x,\theta_m) fM?(x)=m=1∑M?T(x,θm?)
- 前向分布算法: L ( y i , f M ( x ) ) = > L [ y i , f M ? 1 ( x ) + T ( x , θ M ) ] L(y_i,f_M(x))=>L[y_i,f_{M-1}(x)+T(x,\theta_M)] L(yi?,fM?(x))=>L[yi?,fM?1?(x)+T(x,θM?)]
- f m ( x ) = f m ? 1 ( x ) + T ( x , θ m ) , f 0 ( x ) = 0 f_m(x)=f_{m-1}(x)+T(x,\theta_m),f_0(x)=0 fm?(x)=fm?1?(x)+T(x,θm?),f0?(x)=0
1.2.3 AdaBoost
AdaBoost基本思想:
将关注的点放在被错误分类的样本上。
- 初始化样本的权重分布矩阵 D m D_m Dm?;
- 使用具有权重分布 D m D_m Dm?的数据集进行学习,得到弱分类器 G m ( x ) G_m(x) Gm?(x);
- 计算 G m ( x ) G_m(x) Gm?(x)在训练数据集上的分类误差率: e m = ∑ i = 1 N w m , i ( 样 本 权 重 ) I ( G m ( x i ) ≠ y i ) e_m=\sum_{i=1}^Nw_{m,i}(样本权重)I(G_m(x_i)\neq y_i) em?=i=1∑N?wm,i?(样本权重)I(Gm?(xi?)?=yi?)
- 计算 G m ( x ) G_m(x) Gm?(x)在强分类器中的比例: α m = 1 2 l o g 1 ? e m e m \alpha_m=\frac {1}{2}log\frac {1-e_m}{e_m} αm?=21?logem?1?em??
- 更新训练集的权重分布: w m + 1 , i = w m , i z m e x p ( ? α m y i G m ( x i ) ) , i = 1 , 2 , . . . , N w_{m+1,i}=\frac{w_{m,i}}{z_m}exp(-\alpha_my_iG_m(x_i)),i=1,2,...,N wm+1,i?=zm?wm,i??exp(?αm?yi?Gm?(xi?)),i=1,2,...,N z m = ∑ i = 1 N w m , i e x p ( ? α m y i G m ( x i ) ) z_m=\sum_{i=1}^{N}w_{m,i}exp(-\alpha_my_iG_m(x_i)) zm?=i=1∑N?wm,i?exp(?αm?yi?Gm?(xi?))
- 重复1-5的步骤构建弱分类器;
- 最终分类器: F ( x ) = s i g n ( ∑ i = 1 N α m G m ( x ) ) F(x)=sign(\sum_{i=1}^N\alpha_mG_m(x)) F(x)=sign(i=1∑N?αm?Gm?(x))
损失函数: L o s s = ∑ i = 1 N e x p ( ? y i F m ( x i ) ) Loss=\sum_{i=1}^Nexp(-y_iF_m(x_i)) Loss=i=1∑N?exp(?yi?Fm?(xi?)) = ∑ i = 1 N e x p ( ? y i F m ? 1 ( x i ) + α m G m ( x i ) ) =\sum_{i=1}^Nexp(-y_iF_{m-1}(x_i)+ \alpha_mG_m(x_i)) =i=1∑N?exp(?yi?Fm?1?(xi?)+αm?Gm?(xi?))
1.2.4 GBDT
GBDT(Gradient Boosting Decision Tree)梯度提升树基本思想:
损失函数(如均方误差)对Y求偏导可以替换之前BDT中拟合残差的思想:
- 加法模型: h ( x ) = ∑ m = 1 M β m f m ( x ) h(x)=\sum_{m=1}^M\beta_mf_m(x) h(x)=m=1∑M?βm?fm?(x)
- 损失函数:
∑
i
=
1
M
L
(
y
i
,
∑
m
=
1
M
f
m
(
x
)
)
\sum_{i=1}^ML(y_i, \sum_{m=1}^Mf_m(x))
i=1∑M?L(yi?,m=1∑M?fm?(x))
∑
m
=
1
M
L
(
y
i
,
h
m
?
1
+
f
m
(
x
)
)
\sum_{m=1}^ML(y_i,h_{m-1}+f_m(x))
m=1∑M?L(yi?,hm?1?+fm?(x))
求解损失函数时采用一阶泰勒展开,从而使得后一个学习器基于前一个学习器的梯度进行学习。
1.2.5 XGBoost
具体见下面内容。
参考博文:
集成学习(Esemble Learning)
2. XGboost详解
基本库的安装与出参数详情
xgbbost库的安装:
# windows
pip install xgboost
pip install --upgrade xgboost
# mac
brew install gcc@7
pip3 install xgboost
使用xgboost库:
import xgboost as xgb
# 读取数据
xgb.DMatrix()
# 设置参数
param = {}
# 训练模型
bst = xgb.train(param)
# 预测结果
bst.predict()
xgboost的参数一览:


sklearn中的xgboost的API参数一览:

2.1 梯度提升树
2.1.1 重要参数:n_estimators
对于梯度提升树而言,分类和回归的结果通过以下方式决定:
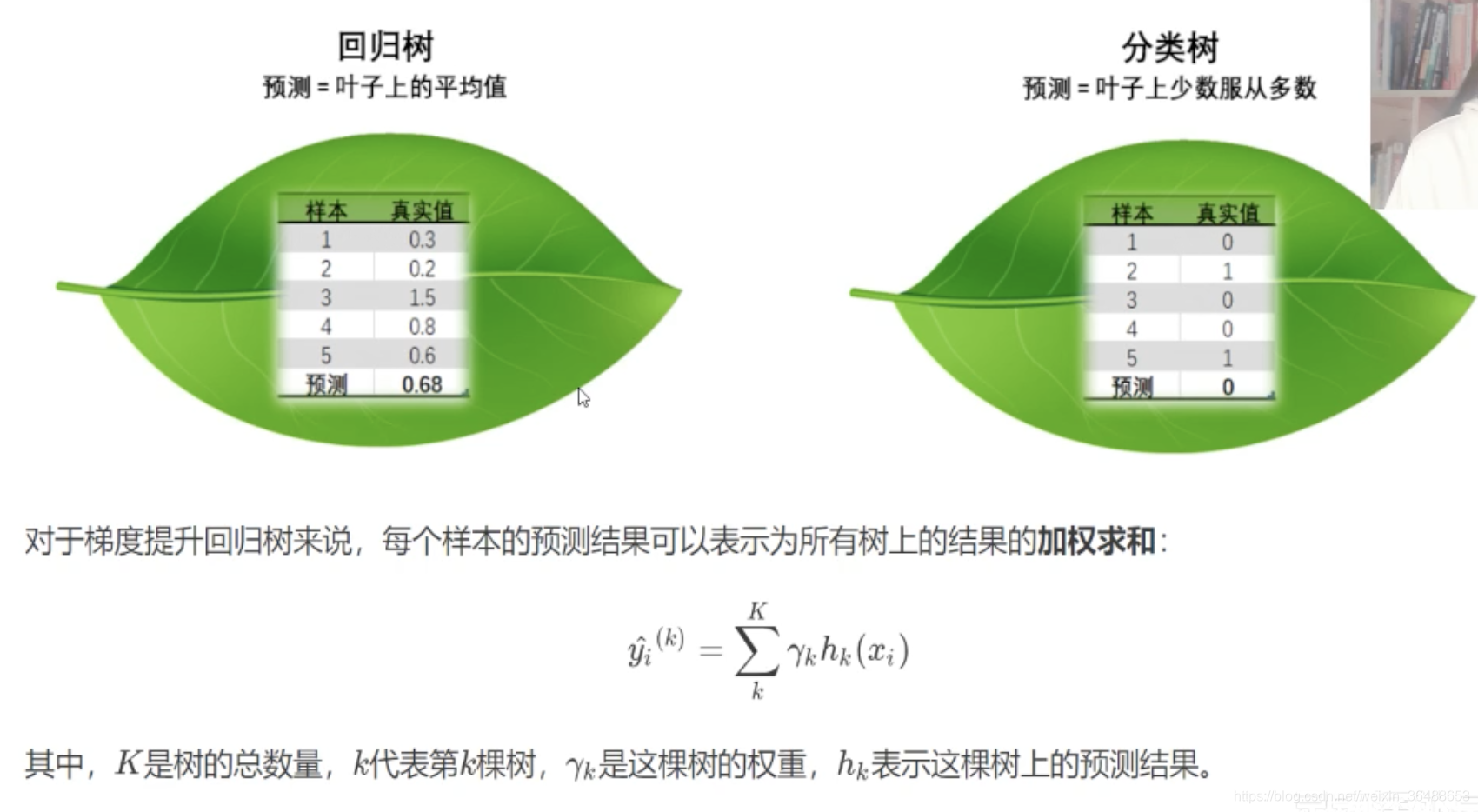
对于XGBoost而言,每个叶子结点上会有一个预测分数,也被称为叶子权重,用
f
k
(
x
i
)
f_k(x_i)
fk?(xi?)或者
ω
\omega
ω来表示,其中
f
k
f_k
fk?表示第
k
k
k棵决策树,
x
i
x_i
xi?表示样本
i
i
i对应的特征向量。假设这个集成模型中共有
K
K
K棵决策树,则整个模型在这个样本
i
i
i上的预测结果为:
y
^
i
k
=
∑
k
K
f
k
(
x
i
)
\hat y_i^k=\sum_k^{K}f_k(x_i)
y^?ik?=k∑K?fk?(xi?)
xgboost和sklearn中API决定树的数量的超参数:
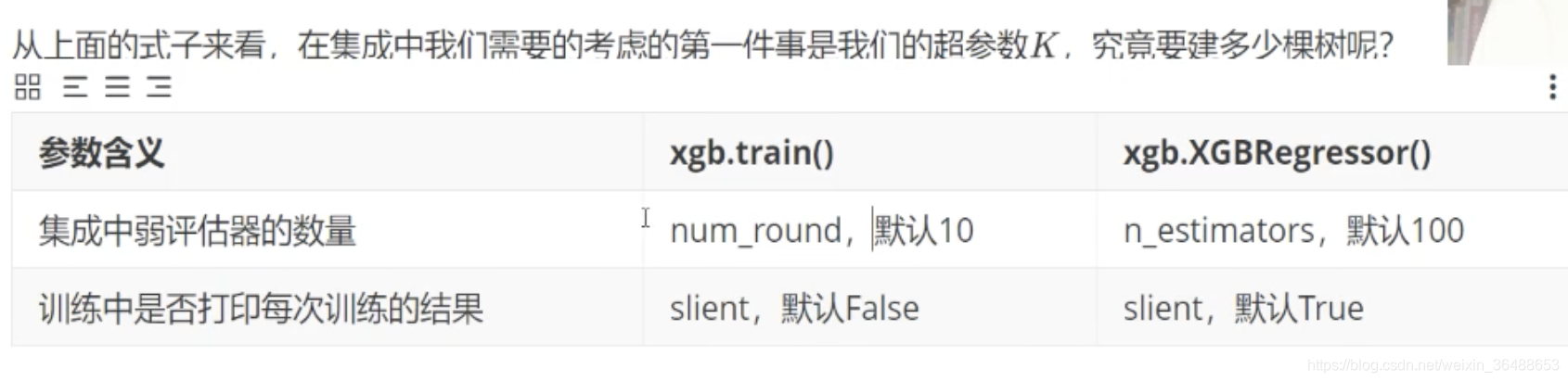
简单使用:
from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LinearR
from sklearn.datasets import load_boston
from sklearn.model_selection import KFold, cross_val_score as CVS, train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime
data = load_boston()
X = data.data
y = data.target
Xtrain, Xtest, Ytrain, Ytest = TTS(X, y, test_size=0.3, random_state=420)
# 不同模型的对比
reg = XGBR(n_estimators=100).fit(Xtrain, Ytrain)
reg.predict(Xtest)
print(reg.score(Xtest, Ytest))
print(MSE(Ytest, reg.predict(Xtest)))
# 查看模型重要性分数(树模型的优势)
print(reg.feature_importances_)
reg = XGBR(n_estimators=100)
print(CVS(reg, Xtrain, Ytrain, cv=5).mean())
print(CVS(reg, Xtrain, Ytrain, cv=5, scoring="neg_mean_aquares_score").mean())
print(sorted(sklearn.metrics.SCORERS.keys()))
rfr = RFR(n_estimators=100)
print(CVS(rfr, Xtrain, Ytrain, cv=5).mean())
print(CVS(rfr, Xtrain, Ytrain, cv=5, scoring="neg_mean_aquares_score").mean())
lr = LinearR()
print(CVS(lr, Xtrain, Ytrain, cv=5).mean())
print(CVS(lr, Xtrain, Ytrain, cv=5, scoring="neg_mean_aquares_score").mean())
# 查看建树的过程,打印进度
reg = XGBR(n_estimators=100, silent=False).fit(Xtrain, Ytrain)
print(CVS(reg, Xtrain, Ytrain, cv=5, scoring="neg_mean_aquares_score").mean())
# 绘制学习曲线函数
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as plt
import numpy as np
def plot_learning_curve(estimator, title, X, y, ax=None, ylim=None, cv=None, n_jobs=None):
train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, shuffle=True, cv=cv,
random_state=420, n_jobs=n_jobs)
if ax == None:
ax = plt.gca()
else:
ax = plt.figure()
ax.set_title(title)
if ylim:
ax.set_ylim(*ylim)
ax.set_xlabel("Training examples")
ax.set_ylabel("Score")
ax.grid()
ax.plot(train_sizes, np.mean(train_scores, axis=1), "o-", color='r', label="Training score")
ax.plot(train_sizes, np.mean(test_scores, axis=1), "o-", color='g', label="Test score")
ax.legend(loc="best")
return ax
cv = KFold(n_splits=5, shuffle=True, random_state=42)
plot_learning_curve(XGBR(n_estimators=100, random_state=420), "XGB", Xtrain, Ytrain, ax=None, cv=cv)
plt.show()
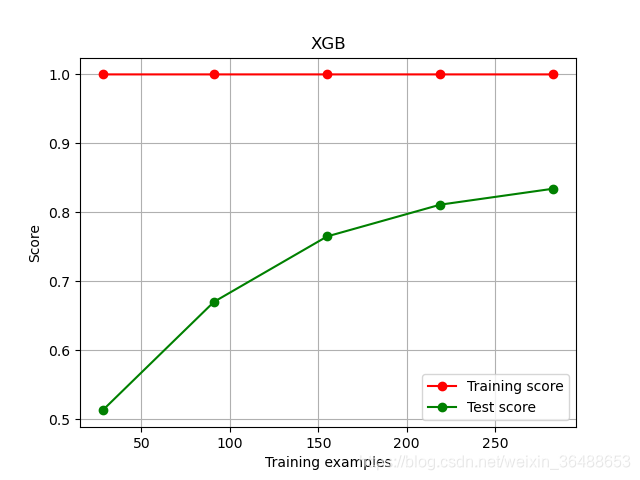
# 使用学习曲线观察n_estimators对模型的影响
# 绘制学习曲线
cv = KFold(n_splits=5, shuffle=True, random_state=42)
axisx = range(10, 1010, 50)
rs = []
for i in axisx:
reg = XGBR(n_estimators=i, random_state=420)
rs.append(CVS(reg, Xtrain, Ytrain, cv=cv).mean())
print(axisx[rs.index(max(rs))], max(rs)) # 160 0.8320776498992342
plt.figure(figsize=(20, 5))
plt.plot(axisx, rs, c="red", label="XGB")
plt.legend()
plt.show()
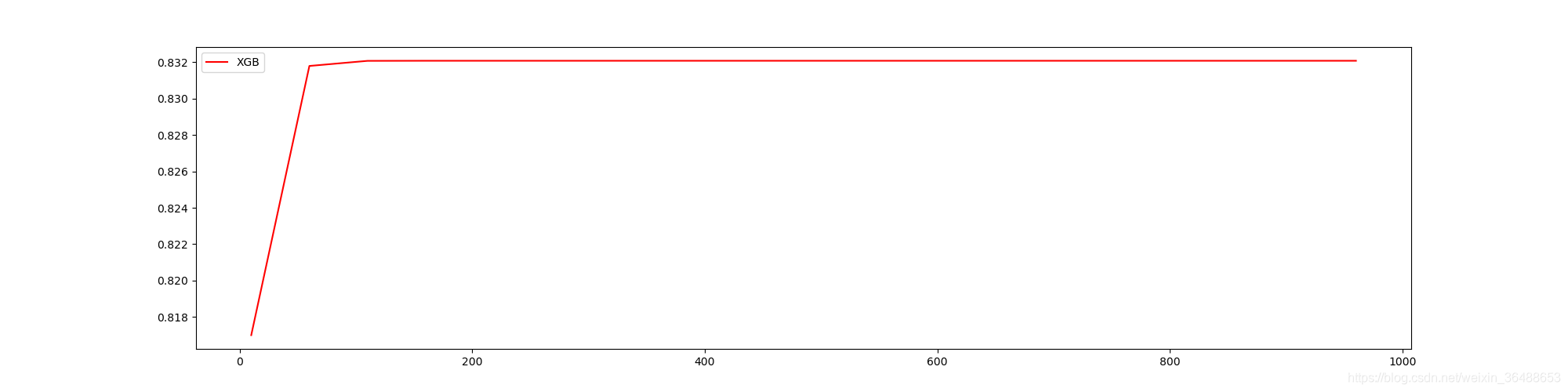
# 进化的学习曲线:方差与泛化误差
axisx = range(50, 1050, 50)
# 细化范围range(100, 300, 10)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=i, random_state=420)
cvresult = CVS(reg, Xtrain, Ytrain, cv=cv)
# 记录偏差
rs.append(cvresult.mean())
# 记录方差
var.append(cvresult.var())
# 计算泛化误差的可控部分
ge.append(1 - cvresult.mean() ** 2 + cvresult.var())
# 打印R2最高所对应的参数取值, 并打印这个参数下的防擦好
print(axisx[rs.index(max(rs))], max(rs), var[rs.index(max(rs))])
# 打印方差最低时对应的参数取值, 并打印这个参数下的R2
print(axisx[var.index(min(var))], rs[var.index(min(var))], min(var))
# 打印泛化误差可控部分的参数取值,并打印这个参数下的R2,方差以及泛化误差的可控部分
print(axisx[ge.index(min(ge))], rs[ge.index(min(ge))], var[ge.index(min(ge))], min(ge))
# 增加方差线的绘制
rs = np.array(rs)
var = np.array(var) * 0.01
plt.figure(figsize=(20, 5))
plt.plot(axisx, rs, c="black", label="XGB")
plt.plot(axisx, rs+var, c="red", linestyle="-.")
plt.plot(axisx, rs-var, c="red", linestyle="-.")
plt.legend()
plt.show()
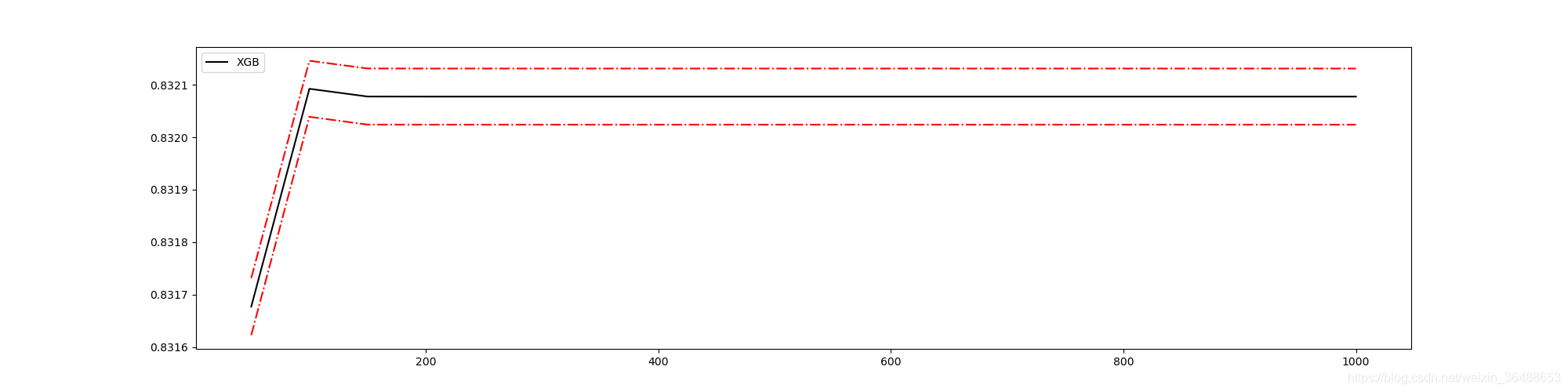
验证模型效果:
time0 = time()
print(XGBR(n_estimators=100, random_state=420).fit(Xtrain, Ytrain).score(Xtest, Ytest))
print(time()-time0)
# 0.9050988968414799
# 0.13734769821166992
time0 = time()
print(XGBR(n_estimators=660, random_state=420).fit(Xtrain, Ytrain).score(Xtest, Ytest))
print(time()-time0)
# 0.9050526026617368
# 0.38094520568847656
time0 = time()
print(XGBR(n_estimators=180, random_state=420).fit(Xtrain, Ytrain).score(Xtest, Ytest))
print(time()-time0)
# 0.9050526026617368
# 0.18987488746643066
2.1.2 重要参数:subsample
对于大样本数据集(小样本就不随机采样),如果每次构建树都用全数据会导致运行时间过长,因此采取有放回抽样的方式来抽取样本构建树,每一棵树结束训练后会反馈预测错误的样本结果,因此在构建下一棵树时,会加重上一棵树被预测错误样本的权重,以此类推直到最后。
参数一览(抽取样本的比例):

# 绘制参数学习曲线
axisx = np.linspace(0, 1, 20)
# 细化:axisx = np.linspace(0.05, 1, 20)
rs = []
for i in axisx:
reg = XGBR(n_estimators=100, subsample=i, random_state=420)
rs.append(CVS(reg, Xtrain, Ytrain, cv=cv).mean())
print(axisx[rs.index(max(rs))], max(rs))
# 1.0 0.8320924293483107
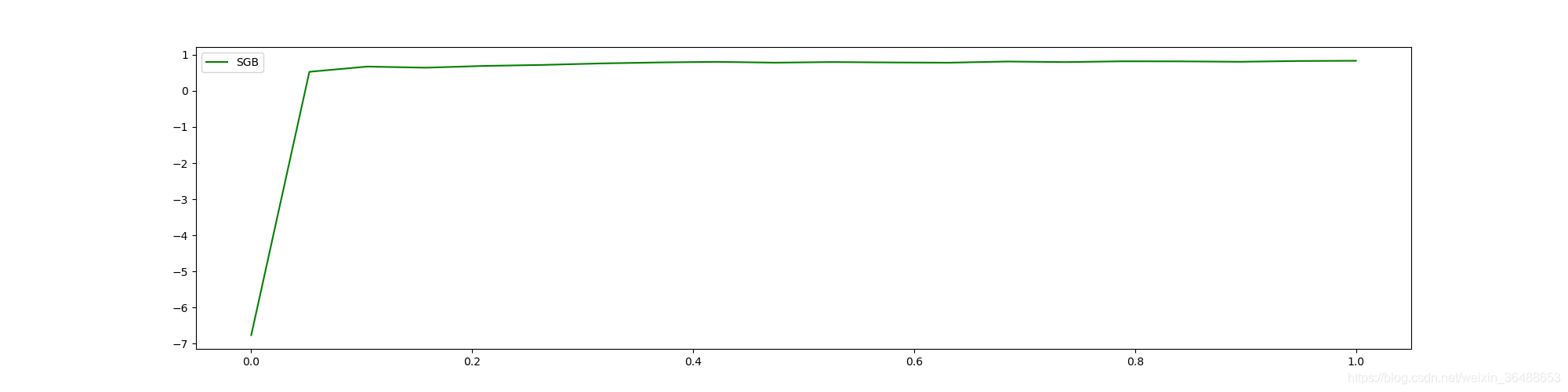
plt.figure(figsize=(20, 5))
plt.plot(axisx, rs, c="green", label="SGB")
plt.legend()
plt.show()
# 也可以考虑方差偏差进一步细化,如上就不写了
reg = XGBR(n_estimators=180, subsample=0.770833333333334, random_state=420).fit(Xtrain, Ytrain)
print(reg.score(Xtest, Ytest))
print(MSE(Ytest, reg.predict(Xtest)))
2.1.3 重要参数:eta
在XGBoost中,完整的迭代决策树的公式:
y
^
i
(
k
+
1
)
=
y
^
i
(
k
)
+
η
f
k
+
1
(
x
i
)
\hat y_i^{(k+1)}=\hat y_i^{(k)}+\eta f_{k+1}(x_i)
y^?i(k+1)?=y^?i(k)?+ηfk+1?(xi?)
其中
η
\eta
η读作eta,是迭代决策树的步长,又叫学习率。

# 定义一个评分函数,直接打印Xtrain上交叉验证的结果
def regassess(reg, Xtrain, Ytrain, cv, scoring=["r2"], show=True):
score = []
for i in range(len(scoring)):
if show:
print("{}:{:.2f}".format(scoring[i], CVS(reg, Xtrain, Ytrain, cv=cv, scoring=scoring[i]).mean()))
score.append(CVS(reg, Xtrain, Ytrain, cv=cv, scoring=scoring[i]).mean())
return score
# 查看learning_rate的影响
for i in [0, 0.2, 0.5, 1]:
time0 = time()
reg = XGBR(n_estimators=180, random_state=420, learning_rate=i)
print("learning_rate = {}".format(i))
regassess(reg, Xtrain, Ytrain, cv, scoring=["r2", "neg_mean_squared_error"])
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
print("\t")
"""
learning_rate = 0
r2:-6.76
neg_mean_squared_error:-567.55
00:03:225483
learning_rate = 0.2
r2:0.83
neg_mean_squared_error:-12.30
00:04:164096
learning_rate = 0.5
r2:0.82
neg_mean_squared_error:-12.48
00:02:290789
learning_rate = 1
r2:0.71
neg_mean_squared_error:-20.06
00:01:632761
"""
# 可以根据上述步骤绘制方差等复杂的学习曲线
2.2 XGBoost进阶
2.2.1 选择弱评估器:重要参数booster

for booster in ["gbtree", "gblinear", "dart"]:
reg = XGBR(n_estimators=180, learning_rate=0.1, random_state=420, booster=booster).fit(Xtrain, Ytrain)
print(booster)
print(reg.score(Xtest, Ytest))
"""
gbtree
0.9260984369386971
gblinear
0.6521127945547635
dart
0.9260984459922119
"""
2.2.2 目标函数:重要参数objective
XGBoost引入了模型复杂度来衡量算法的运算效率,目标函数被写作:
O
b
j
=
∑
i
=
1
m
l
(
y
i
,
y
^
i
)
+
∑
k
=
1
K
Ω
(
f
k
)
Obj=\sum_{i=1}^{m}l(y_i,\hat y_i)+\sum_{k=1}^{K}\Omega(f_k)
Obj=i=1∑m?l(yi?,y^?i?)+k=1∑K?Ω(fk?)
其中
i
i
i代表数据集中的第
i
i
i个样本,
m
m
m表示导入第
k
k
k棵树的数据总量,
K
K
K代表所有树的总数,当只建立了
t
t
t棵树时,式子应当为
∑
k
=
1
t
Ω
(
f
k
)
\sum_{k=1}^{t}\Omega(f_k)
∑k=1t?Ω(fk?)。第一项是常用的损失项如RMSE。第二项代表模型复杂度。

采用xgboost本身的库(样本更大,效果更好且速度更快):
import xgboost as xgb
# 使用Dmatrix读取数据
dtrain = xgb.DMatrix(Xtrain, Ytrain)
dtest = xgb.DMatrix(Xtest, Ytest)
# 写明参数
param = {"silent":False, "objective": "reg:linear", "eta": 0.1}
num_round = 180
# 类train
bst = xgb.train(param, dtrain, num_round)
preds = bst.predict(dtest)
r2_score(Ytest, preds)
MSE(Ytest, preds)
2.2.3 求解XGB目标函数
在求解XGB目标函数的过程中,可以将目标函数转化为更为简单的形式。已知:
y
^
i
(
t
)
=
∑
k
t
f
k
(
x
i
)
=
∑
k
t
?
1
f
k
(
x
i
)
+
f
t
(
x
i
)
=
y
^
i
t
?
1
+
f
t
(
x
i
)
\hat y_i^{(t)}=\sum_k^{t}f_k(x_i) =\sum_k^{t-1}f_k(x_i) + f_t(x_i)=\hat y_i^{t-1}+ f_t(x_i)
y^?i(t)?=k∑t?fk?(xi?)=k∑t?1?fk?(xi?)+ft?(xi?)=y^?it?1?+ft?(xi?)
目标函数可以看作两部分:
O
b
j
=
∑
i
=
1
m
l
(
y
i
,
y
^
i
)
+
∑
k
=
1
K
Ω
(
f
k
)
Obj=\sum_{i=1}^{m}l(y_i,\hat y_i)+\sum_{k=1}^{K}\Omega(f_k)
Obj=i=1∑m?l(yi?,y^?i?)+k=1∑K?Ω(fk?)
拆开进行简化。
首先第一个部分:
在第t次迭代中,有上述已知式子可得:
∑
i
=
1
m
l
(
y
i
,
y
^
i
)
\sum_{i=1}^{m}l(y_i,\hat y_i)
i=1∑m?l(yi?,y^?i?)
=
∑
i
=
1
m
l
(
y
i
t
,
y
^
i
t
?
1
+
f
t
(
x
i
)
)
=\sum_{i=1}^ml(y_i^t,\hat y_i^{t-1}+ f_t(x_i))
=i=1∑m?l(yit?,y^?it?1?+ft?(xi?))
由于
y
i
t
y_i^t
yit?是一个已知项,则可以表示成:
=
F
(
y
^
i
(
t
?
1
)
+
f
t
(
x
i
)
)
=F(\hat y_i^{(t-1)}+f_t(x_i))
=F(y^?i(t?1)?+ft?(xi?))
由泰勒公式二阶展开,该表达式可以简化:
f
(
x
1
+
x
2
)
≈
f
(
x
1
)
+
x
2
?
f
′
(
x
1
)
+
1
2
(
x
2
)
2
?
f
′
′
(
x
1
)
f(x_1+x_2)\approx f(x_1)+x_2*f'(x_1)+\frac {1}{2}(x_2)^2*f''(x_1)
f(x1?+x2?)≈f(x1?)+x2??f′(x1?)+21?(x2?)2?f′′(x1?)
F
(
y
^
i
(
t
?
1
)
+
f
t
(
x
i
)
)
≈
F
(
y
^
i
(
t
?
1
)
)
+
f
t
(
x
i
)
?
?
F
(
y
^
i
(
t
?
1
)
)
?
y
^
i
(
t
?
1
)
+
1
2
(
(
f
t
(
x
i
)
)
2
)
?
?
2
F
(
y
^
i
(
t
?
1
)
)
?
y
^
i
(
t
?
1
)
F(\hat y_i^{(t-1)}+f_t(x_i))\approx F(\hat y_i(t-1))+f_t(x_i)*\frac {\partial F(\hat y_i^{(t-1)})}{\partial \hat y_i^{(t-1)}}+\frac {1}{2}((f_t(x_i))^2)*\frac {\partial ^2F(\hat y_i^{(t-1)})}{\partial \hat y_i^{(t-1)}}
F(y^?i(t?1)?+ft?(xi?))≈F(y^?i?(t?1))+ft?(xi?)??y^?i(t?1)??F(y^?i(t?1)?)?+21?((ft?(xi?))2)??y^?i(t?1)??2F(y^?i(t?1)?)?
≈
l
(
y
i
t
,
y
^
i
(
t
?
1
)
)
+
f
t
(
x
i
)
?
g
i
+
1
2
(
f
t
(
x
i
)
)
2
?
h
i
\approx l(y_i^t,\hat y_i^(t-1))+f_t(x_i)*g_i+\frac {1}{2}(f_t(x_i))^2*h_i
≈l(yit?,y^?i(?t?1))+ft?(xi?)?gi?+21?(ft?(xi?))2?hi?
=
∑
i
=
1
m
[
l
(
y
i
t
,
y
^
i
(
t
?
1
)
)
+
f
t
(
x
i
)
g
i
+
1
2
(
f
t
(
x
i
)
)
2
h
i
]
=\sum_{i=1}^{m}[l(y_i^t,\hat y_i^{(t-1)})+f_t(x_i)g_i+\frac {1}{2}(f_t(x_i))^2h_i]
=i=1∑m?[l(yit?,y^?i(t?1)?)+ft?(xi?)gi?+21?(ft?(xi?))2hi?]
第二个部分:
∑
k
=
1
K
Ω
(
f
k
)
\sum_{k=1}^{K}\Omega (f_k)
k=1∑K?Ω(fk?)
=
∑
k
=
1
t
?
1
Ω
(
f
k
)
+
Ω
(
f
t
)
=\sum_{k=1}^{t-1}\Omega (f_k)+\Omega (f_t)
=k=1∑t?1?Ω(fk?)+Ω(ft?)
则目标函数最终可以被简化成:
∑
i
=
1
m
[
f
t
(
x
i
)
g
i
+
1
2
(
f
t
(
x
i
)
)
2
h
i
)
]
+
Ω
(
f
t
)
\sum_{i=1}^{m}[f_t(x_i)g_i+\frac {1}{2}(f_t(x_i))^2h_i)]+\Omega (f_t)
i=1∑m?[ft?(xi?)gi?+21?(ft?(xi?))2hi?)]+Ω(ft?)
在GBDT中求解一阶导数是为了求解极值,XGBoost采用二阶导数是为了简化公式,两个过程是不可类比的,并且在XGBoost中求解极值也是求解一阶导数。
2.2.4 参数化决策树:参数alpha、lambda
若使用
q
(
x
i
)
q(x_i)
q(xi?)表示样本
x
i
x_i
xi?所在的叶子节点,并且使用
w
q
(
x
i
)
w_{q(x_i)}
wq(xi?)?来表示这个样本落到第
k
k
k棵树上的第
q
(
x
i
)
q(x_i)
q(xi?)个叶子节点中所获得的分数,于是有:
f
k
(
x
i
)
=
w
q
(
x
i
)
f_k(x_i)=w_{q(x_i)}
fk?(xi?)=wq(xi?)?
树的复杂度可以表示为(叶子数可以反推出深度):
Ω
(
f
)
=
γ
T
+
正
则
项
(
L
1
或
L
2
或
两
个
一
起
)
\Omega(f)=\gamma T+正则项(L1或L2或两个一起)
Ω(f)=γT+正则项(L1或L2或两个一起)
XGBoost和GBDT的一个核心区别就在于XGBoost引入了正则项来控制过拟合。

分类型的模型一般不考虑正则项。
from sklearn.model_selection import GridSearchCV
# 使用网格搜索来寻找参数最佳组合
param = {"reg_alpha": np.arange(0, 5, 0.05), "reg_lambda":np.arange(0, 2, 0.05)}
reg = XGBR(n_estimators=180, learning_rate=0.1, random_state=420)
gscv = GridSearchCV(reg, param_grid=param, scoring="neg_mean_aquared_error", cv=cv)
time0 = time()
gscv.fit(Xtrain, Ytrain)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%s:%f"))
print(gscv.best_params_)
print(gscv.best_score_)
preds = gscv.predict(Xtest)
print(r2_score(Ytest, preds))
print(MSE(Ytest, preds))
2.2.5 寻找最佳树结构:求解 ω \omega ω与 T T T
根据上一节的基础,目标函数可以进一步进行修改,所有结构都转换成同叶子节点数相关:
∑
i
=
1
m
[
f
t
(
x
i
)
g
i
+
1
2
(
f
t
(
x
i
)
)
2
h
i
)
]
+
Ω
(
f
t
)
\sum_{i=1}^{m}[f_t(x_i)g_i+\frac {1}{2}(f_t(x_i))^2h_i)]+\Omega (f_t)
i=1∑m?[ft?(xi?)gi?+21?(ft?(xi?))2hi?)]+Ω(ft?)
=
∑
i
=
1
m
[
w
q
(
x
i
)
+
1
2
w
q
(
x
i
)
2
h
i
]
+
γ
T
+
1
2
∑
j
=
1
T
w
j
2
=\sum_{i=1}^m[w_{q(x_i)}+\frac {1}{2}w_{q(x_i)}^2h_i]+\gamma T+\frac {1}{2}\sum_{j=1}^Tw_j^2
=i=1∑m?[wq(xi?)?+21?wq(xi?)2?hi?]+γT+21?j=1∑T?wj2?
由于每个叶子只有一个权重值,有差别的是每个样本对应的一阶导
g
i
g_i
gi?,则可以进一步转换:
∑
j
=
1
T
(
w
j
?
∑
i
∈
I
j
+
1
2
∑
j
=
1
T
(
w
j
2
?
∑
i
∈
I
j
h
i
)
)
+
γ
T
+
1
2
∑
j
=
1
T
w
j
2
\sum_{j=1}^T(w_j*\sum_{i\in I_j}+\frac{1}{2}\sum_{j=1}^T(w_j^2*\sum_{i\in I_j}h_i))+\gamma T+\frac {1}{2}\sum_{j=1}^Tw_j^2
j=1∑T?(wj??i∈Ij?∑?+21?j=1∑T?(wj2??i∈Ij?∑?hi?))+γT+21?j=1∑T?wj2?
=
∑
j
=
1
T
[
w
j
∑
i
∈
I
j
g
i
+
1
2
w
j
2
(
∑
i
∈
I
j
h
i
+
λ
)
]
+
γ
T
=\sum_{j=1}^T[w_j\sum_{i\in I_j}g_i+\frac {1}{2}w_j^2(\sum_{i\in I_j}h_i+\lambda)]+\gamma T
=j=1∑T?[wj?i∈Ij?∑?gi?+21?wj2?(i∈Ij?∑?hi?+λ)]+γT
用
G
i
G_i
Gi?和
H
j
H_j
Hj?分别表示一阶导和二阶导的加和,则有:
o
b
j
(
t
)
=
∑
j
=
1
T
[
w
j
G
j
+
1
2
w
j
2
(
H
j
+
λ
)
]
obj^{(t)}=\sum_{j=1}^T[w_jG_j+\frac{1}{2}w_j^2(H_j+\lambda)]
obj(t)=j=1∑T?[wj?Gj?+21?wj2?(Hj?+λ)]
F
?
(
w
j
)
=
w
j
G
j
+
1
2
w
j
2
=
(
H
j
+
λ
)
F^*(w_j)=w_jG_j+\frac{1}{2}w_j^2=(H_j+\lambda)
F?(wj?)=wj?Gj?+21?wj2?=(Hj?+λ)
为了使得目标函数最小,则可以基于
F
?
(
w
j
)
F^*(w_j)
F?(wj?)对
w
j
w_j
wj?求解一阶导数,则有:
w
j
=
?
G
j
H
j
+
λ
w_j=-\frac {G_j}{H_j+\lambda}
wj?=?Hj?+λGj??
将该式子带入原式中可得:
O
b
j
(
t
)
=
?
1
2
∑
j
=
1
T
G
j
2
H
j
+
λ
+
γ
T
Obj^{(t)}=-\frac{1}{2}\sum_{j=1}^T\frac {G_j^2}{H_j+\lambda}+\gamma T
Obj(t)=?21?j=1∑T?Hj?+λGj2??+γT
此时目标函数被简化成“结构分数”,只和叶子节点个数有关。
根据决策树选取叶子节点时根据信息增益的原则,在构建XGBoost树时也可以采用这样的策略,根据目标函数减小的最大的方向来构建我们的树,进行分支,达到局部最优。
2.2.5 让树停止生长:重要参数gamma

调整gamma可以调整模型的泛化能力,通过简化后的公式可以看出gamma可以调整树的深度:
# gamma学习曲线
axisx = np.arange(0, 5, 0.05)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=180, random_state=420, gamma=i)
result = CVS(reg, Xtrain, Ytrain, cv=cv)
rs.append(result.mean())
var.append(result.var())
ge.append((1 - result.mean()) ** 2 + result.var())
rs = np.array(rs)
var = np.array(var) * 0.1
plt.figure(figsize=(20, 5))
plt.plot(axisx, rs, c="black", label="XGB")
plt.plot(axisx, rs + var, c="red", linestyle="-.")
plt.plot(axisx, rs - var, c="red", linestyle="-.")
plt.legend()
plt.show()
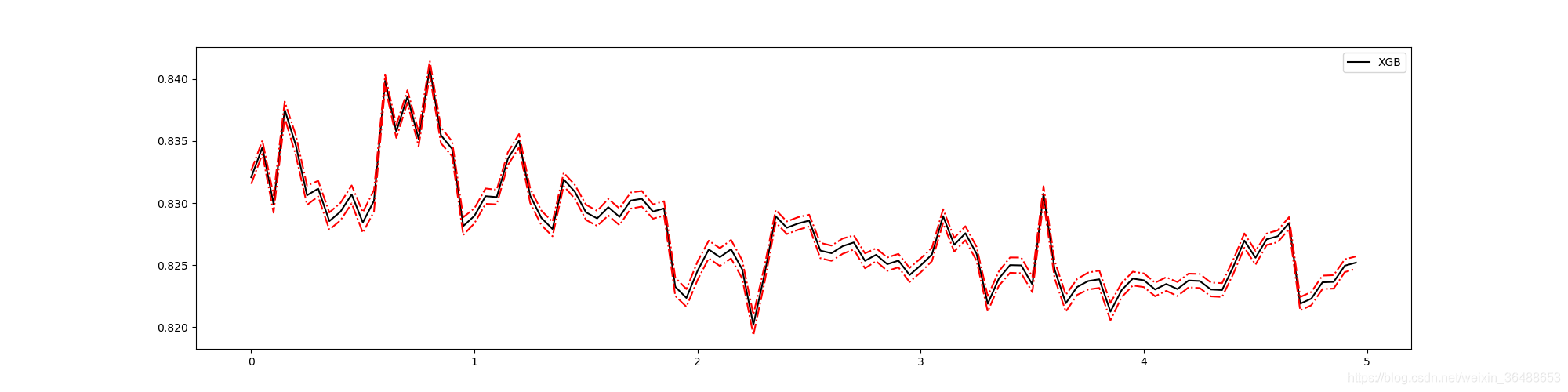
xgboost.cv的使用(更好地查看参数对模型的影响):
import xgboost as xgb
#xgb.cv的使用
dfull = xgboost.DMatrix(X, y)
# "eval_metric":[rmse, mae, logloss, mlogloss, error, auc]
param1 = {"silent": True, "objective": "reg:linear", "gamma": 0}
num_round = 180
n_fold = 5
time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round, n_fold)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%s:%f"))
print(cvresult1)
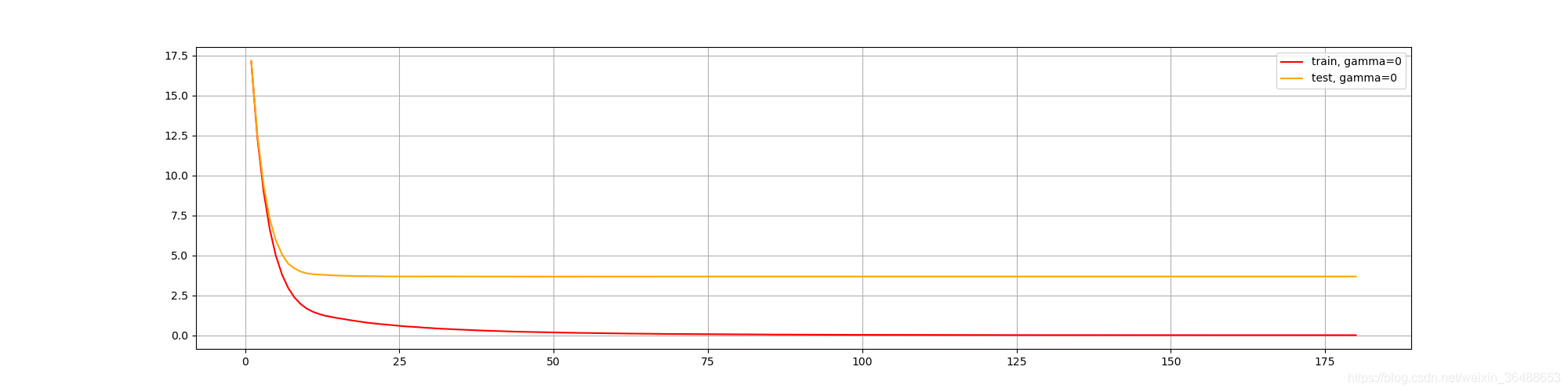
plt.figure(figsize=(20, 5))
plt.grid()
plt.plot(range(1, 181), cvresult1.iloc[:, 0], c="red", label="train, gamma=0")
plt.plot(range(1, 181), cvresult1.iloc[:, 2], c="orange", label="test, gamma=0")
plt.legend()
plt.show()
2.3 XGBoost应用扩展
2.3.1 过拟合:剪枝参数
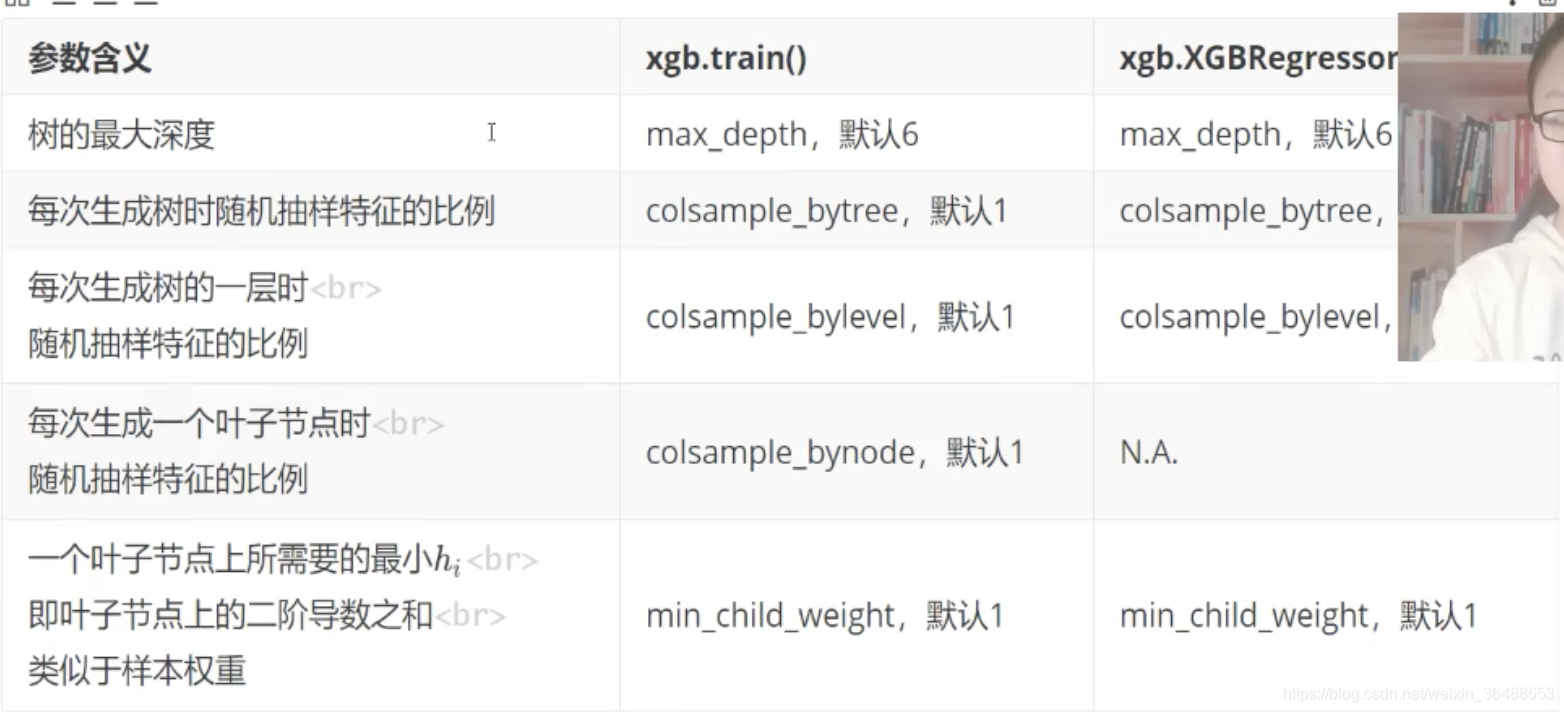
观察默认参数表现:
dfull = xgb.Dmatrix(X,y)
param1 = {"silent": True
, "obj": "reg:linear"
, "subsample": 1
, "max_depth": 6
, "eta": 0.3
, "gamma": 0
, "lambda": 1
, "alpha": 0
, "colsample_bytree": 1
, "colsapmle_bylevel": 1
, "colsample_bynode": 1
, "nfold": 5}
num_round = 200
# 观察默认参数表现
time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%F"))
fig, ax = plt.subplots(1, figsize=(15, 10))
ax.grid()
ax.plot(range(1, 201), cvresult1.iloc[:, 0], c="red", label="train,original")
ax.plot(range(1, 201), cvresult1.iloc[:, 2], c="orange", label="test,original")
ax.legend(fontsize="xx-large")
plt.show()
# 直接通过修改param来调整参数
# 保存和加载模型
from joblib import dump
bst = xgb.train(param1, dfull, num_round)
dump(bst, "模型命名")
bst = joblib.load("模型命名")
# or
import pickle
pickle.dump(bst, open("xgboost.dat", "wb"))
bst = pickle.load(open("xgboost.dat", "rb"))
2.3.2 XGBoost分类样本不均衡

参数是:负样本数/正样本数。
查看该参数的作用:
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split as TTS
from xgboost import XGBClassifier as XGBC
from sklearn.metrics import confusion_matrix as cm, recall_score as recall, roc_auc_score as auc
# 人为创造不均衡样本
class_1 = 500
class_2 = 50
# 设定两个类别的中心
centers = [[0.0, 0.0], [2.0, 2.0]]
# 设定两个类别的方差
clusters_std = [1.5, 0.5]
X, y = make_blobs(n_samples=[class_1, class_2],
centers=centers,
clusters_std=clusters_std,
random_state=0,
shuffle=False)
Xtrain, Xtest, Ytrain, Ytest = TTS(X, y, test_size=0.3, random_state=420)
clf_ = XGBC(scale_pos_weight=10).fit(Xtrain)
ypred = clf_.predict(Xtest)
clf_.score(Xtest, Ytest)
cm(Ytest, ypred, labels=[1, 0])
recall(Ytest, ypred)
auc(Ytest, clf_.predict_proba(Xtest)[:, 1])
for i in [1, 5, 10, 20, 30]:
clf_ = XGBC(scale_pos_weight=i).fit(Xtrain, Ytrain)
ypred_ = clf_.predict(Xtest)
print(i)
print("\tAccuracy:{}".format(clf_.score(Xtest, Ytest)))
print("\tRecall:{}".format(recall(Xtest, ypred_)))
print("\tAccuracy:{}".format(Ytest, clf_.predict_proba(Xtest)[:, 1]))
使用XGBoost本身:
dtrain = xgb.Dmatrix(Xtrain, Ytrain)
dtest = xgb.Dmatrix(Xtest, Ytest)
param = {"silent":True, "objective": "binary:logistic", "eta": 0.1, "scale_pos_weight":1}
num_round = 100
bst = xgb.trian(param, dtrain, num_round)
preds = bst.predict(dtest)
ypred = preds.copy()
# 可以自己设定阈值
ypreds[preds > 0.5] = 1
ypreds[preds != 1] = 0
# 写明参数
scale_pos_weight = [1, 5, 10]
names = ["negative vs positive: 1", "negative vs positive: 5", "negative vs positive: 10"]
for name, i in zip(names, scale_pos_weight):
param = {"silent":True, "objective": "binary:logistic", "eta": 0.1, "scale_pos_weight":i}
clf = xgb.train(param, dtrain, num_round)
preds = clf.predict(dtest)
ypred = preds.copy()
ypred[preds > 0.5] = 1
ypred[ypred != 1] = 0
print(name)
print("\tAccuracy:{}".format(clf_.score(Xtest, Ytest)))
print("\tRecall:{}".format(recall(Xtest, ypred_)))
print("\tAccuracy:{}".format(Ytest, clf_.predict_proba(Xtest)[:, 1]))