写在前面
经过周末的休息,脑子得到了足够的休息,所以今天调程序的时候就特别顺利,完成了标准BP神经网络的程序搭建,并且开始了参数的调整,那么今天这篇博客主要分析程序实现以及模型调优的尝试过程。
神经网络
最终我确定下来的神经网络长这样:

相较于之前的模型,我将神经网络的输入层增加到了2个神经元,一个是图像的熵率,一个是图像的颜色距离,两者的计算方法如下图所示:
def calcuEntImagedist(x):
x_out = np.zeros(((1, 2)), dtype=float)
gray_temp = np.zeros((1, 256), dtype=float)
for i in range(0, 784):
temp = int(x[i])
gray_temp[0][temp] = gray_temp[0][temp] + 1
sum_tmp = float(0)
for i in range(0, 256):
gray_temp[0][i] = gray_temp[0][i] / 784
result = float(0)
for i in range(0, 256):
if(gray_temp[0][i] > 0):
result = result - gray_temp[0][i] * np.log2(gray_temp[0][i])
# print(result)
for i in range(0, 784):
sum_tmp = sum_tmp + x[i]
sum_tmp = sum_tmp / 784
temp_s = float(0)
for i in range(0 ,784):
temp_s = temp_s + pow((x[i] - sum_tmp), 3)
temp_s = pow((temp_s/784),(1/3))
# print(temp_s)
x_out[0][0] = result
x_out[0][1] = temp_s
# print("x_out:", x_out)
return x_out
熵率的计算方法是先遍历整张图,求出每个像素点的数值,然后计算256个像素点出现的概率,最后计算熵率。图像间像素的距离就是先求像素均值,再求各像素点与均值的距离。
公式推导
修改之后的神经网络公式如下图所示,首先是输入层到输出层的传递公式:

下面是输出层到输入层的梯度表示:

输入层到输出层的程序实现如下图所示,主要通过矩阵乘法实现:
m = np.dot(input_x, w) - theta_1
# print(m)
for i in range(0, 4):
m[0][i] = sigmoid(m[0][i])
n = np.dot(m, v) - theta_2
for i in range(0, 4):
n[0][i] = sigmoid(n[0][i])
y_out = np.dot(n, gamma) - theta_3
y_out = sigmoid(y_out)
输出层到输入层的梯度求导公式的程序实现如下图所示,之前尝试换了一个激励函数ReLU,但是后来发现激励函数换了的话整个梯度求导公式都要换,太麻烦了,所以我还是用回了sigmoid(x):
# update dw,dv,dgama,dtheta_1,dtheta_2,dtheta_3
dtheta_3 = -1 * (y_out - y) * (y_out * (1 - y_out))
for i in range(0, 4):
dtheta_2[0][i] = -1 * (y_out - y) * (y_out * (1 - y_out)) * gamma[i] * \
(n[0][i] * (1 - n[0][i]))
dgamma[i] = (y_out - y) * (y_out * (1 - y_out)) * n[0][i]
for i in range(0, 4):
for j in range(0, 4):
dv[i][j] = (y_out - y) * (y_out * (1 - y_out)) * (n[0][j] * (1 - n[0][j])) * \
gamma[j] * m[0][i]
dtheta_1[0][i] = -1 * (y_out - y) * (y_out * (1 - y_out)) * gamma[j] * \
(n[0][j] * (1 - n[0][j])) * v[i][j] * (m[0][i] * (1 - m[0][i])) + dtheta_1[0][i]
for i in range(0, 2):
for j in range(0, 4):
for k in range(0, 4):
dw[i][j] = dw[i][j] + (y_out - y) * (y_out * (1 - y_out)) * gamma[k] * \
(n[0][i] * (1 - n[0][i])) * v[j][k] * (m[0][i] * (1 - m[0][i])) * input_x[0][i]
# update w,v,gama,theta_1,theta_2,theta_3
for i in range(0, 4):
for j in range(0, 2):
w[j][i] = w[j][i] - study_step * dw[j][i]
# print(w)
for i in range(0, 4):
theta_2[0][i] = theta_2[0][i] + study_step * dtheta_2[0][i]
theta_1[0][i] = theta_1[0][i] + study_step * dtheta_1[0][i]
gamma[i] = gamma[i] - study_step * dgamma[i]
for i in range(0, 4):
for j in range(0, 4):
v[i][j] = v[i][j] - study_step * dv[i][j]
theta_3 = theta_3 + study_step * dtheta_3
程序结果以及参数调优
先放上我的初始化参数和模型结果,我是针对一张图片进行多次循环求参数:
total_n = 60000
# train_aside_n = 48000 #set aside ,0.8-0.2
train_aside_n = 1
study_step = 0.8
epoch = 200
start_rand_max = 0.4
w = np.zeros(((2,4)), dtype=float)#(()) is used to confirm line and row
gamma = np.zeros((4,1), dtype=float)
v = np.zeros((4,4), dtype=float)
theta_1 = np.zeros(((1,4)), dtype=float)
theta_2 = np.zeros(((1,4)), dtype=float)
theta_3 = random.uniform(0,start_rand_max)
m = np.ones(((1,4)), dtype=float)
n = np.ones(((1,4)), dtype=float)
input_x = np.zeros(((1, 2)), dtype=float)
y_out = float(0)
# init para
for i in range(0, 4): # [1,4]
gamma[i] = random.uniform(0,start_rand_max)
theta_1[0][i] = random.uniform(0,start_rand_max)
theta_2[0][i] = random.uniform(0,start_rand_max)
for j in range(0, 4):
v[i][j] = random.uniform(0,start_rand_max)
for k in range(0, 2):
w[k][i] = random.uniform(0, start_rand_max)
模型结果:
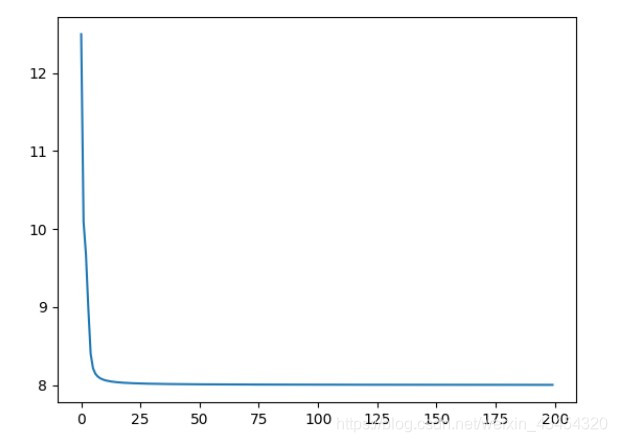
模型下降的结果还不是很满意,明天继续调参,探索参数对于神经网络的影响。我还发现调整了初始化的随机数值对于模型结果的影响很大。

