定义无向网络
An undirected net is a tuple G = ( V , w ) G=\left(\textbf{V},w\right) G=(V,w), where V \textbf{V} V is the set of nodes, and w : V × V → R w: \textbf{V} \times \textbf{V} \to \mathbb{R} w:V×V→R is the weight function where w ( v i , v j ) = w ( v j , v i ) w(v_i,v_j) = w(v_j, v_i) w(vi?,vj?)=w(vj?,vi?) is the weight of the edge ( v i , v j ) (v_i,v_j) (vi?,vj?).
树
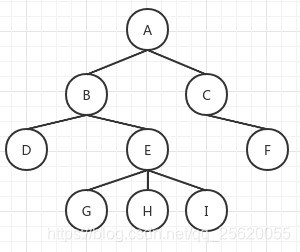
其中
V
=
{
A
,
B
,
C
,
D
,
E
,
F
,
G
,
H
,
I
}
\textbf{V}=\{A,B,C,D,E,F,G,H,I\}
V={A,B,C,D,E,F,G,H,I},
r
=
A
r = A
r=A,
p
(
A
)
=
?
,
p
(
B
)
=
A
,
p
(
C
)
=
A
,
p
(
D
)
=
B
,
p
(
E
)
=
B
,
p
(
F
)
=
C
,
p
(
G
)
=
E
,
p
(
H
)
=
E
,
p
(
I
)
=
E
p(A)=\phi,p(B)=A,p(C)=A,p(D)=B,p(E)=B,p(F)=C,p(G)=E,p(H)=E,p(I)=E
p(A)=?,p(B)=A,p(C)=A,p(D)=B,p(E)=B,p(F)=C,p(G)=E,p(H)=E,p(I)=E
int n = 9;
int root = 0;
int[] parent = {-1, 0, 0, 1, 1, 2, 4, 4, 4};
m m m叉树

int[][] child = {{1,2,3},{-1,4,5},{-1,-1,-1},{-1,6,7},{8,9,-1},{-1,-1,-1},{-1,-1,-1},{-1,-1,-1},{-1,-1,-1},{-1,-1,-1}};
树的字母表定义
Let ? \phi ? be the empty node, a tree is a triple T = ( V , r , Σ , p ) T=(\textbf{V},r,\Sigma,p) T=(V,r,Σ,p) where
- V ≠ ? \textbf{V} \ne \emptyset V?=? is the set of nodes;
- r ∈ V r\in \textbf{V} r∈V is the root node;
- Σ \Sigma Σ is the alphabet with one element;
-
p
:
V
×
Σ
?
→
V
∪
{
?
}
p: \textbf{V} \times \Sigma^* \to \textbf{V} \cup \{\phi\}
p:V×Σ?→V∪{?} is the parent mapping satisfying
- ? s ∈ Σ , st. ? p ( r , s ) = ? ; \forall s \in \Sigma, \text{st.}\, p(r, s) = \phi; ?s∈Σ,st.p(r,s)=?;
- ? v ∈ V , ? 1 s ∈ Σ ? , st. ? p ( v , s ) = r \forall v \in \textbf{V}, \exists1 s \in \Sigma^*,\text{st.}\,p(v,s)=r ?v∈V,?1s∈Σ?,st.p(v,s)=r.
对元祖的理解
元组就是若干个元素的有限有序列表,也代表着元素之间存在某种关系。在图、树、 m m m叉树中定义中都用到了元组,使用元组将点集,顶点等元素结合起来形成新的关系,即数据结构中的逻辑关系。同时,和 Python 中的元组一样,定义中的元组可以包含任意类型的元素,并在定义后不可改变(不能像集合一样进行运算)。