ͼ�������ֱ��ͼ
�������
g = f ? h g=f\otimes h g=f?h
����Ϊ:
g
(
i
,
j
)
=
��
k
,
l
f
(
i
+
k
,
j
+
l
)
h
(
k
,
l
)
g(i,j)=\sum_{k,l}f(i+k,j+l)h(k,l)
g(i,j)=k,l��?f(i+k,j+l)h(k,l)
��3*3��h����Ϊ��,���ê���ھ�������Ļ�,��
(
i
?
1
��
k
��
i
+
1
,
j
?
1
��
l
��
j
+
1
)
(i-1\le k\le i+1,j-1\le l\le j+1)
(i?1��k��i+1,j?1��l��j+1)�����ê�������ϽǵĻ�,��
(
i
��
k
��
i
+
2
,
j
��
l
��
j
+
2
)
(i\le k\le i+2,j\le l\le j+2)
(i��k��i+2,j��l��j+2)��
��������
g = f ? h g=f\ast h g=f?h
����Ϊ:
g
(
i
,
j
)
=
��
k
,
l
f
(
i
?
k
,
j
?
l
)
h
(
k
,
l
)
g(i,j)=\sum_{k,l}f(i-k,j-l)h(k,l)
g(i,j)=k,l��?f(i?k,j?l)h(k,l)
��Ȼ
f
?
h
=
f
?
r
o
t
180
(
h
)
f\ast h=f\otimes rot180(h)
f?h=f?rot180(h)
rotN��ʾ������Ԫ����������ʱ����תN�ȡ�
�ҶȻ�
��RGB��ʽ�IJ�ͼΪ��,ͨ���ҶȻ����õķ�����Ҫ��:
- G r a y = ( R + G + B ) / 3 Gray=(R+G+B)/3 Gray=(R+G+B)/3;
- G r a y = max ? ( R , G , B ) Gray=\max(R,G,B) Gray=max(R,G,B);
- G r a y = 0.299 R + 0.587 G + 0.114 B Gray=0.299R+0.587G+0.114B Gray=0.299R+0.587G+0.114B.
�Ҷ�ֱ��ͼ
�Ҷ�ֱ��ͼ�ǻҶȼ��ĺ���,����ͼ���иûҶȼ������ظ���(��ûҶȼ����س��ֵ�Ƶ��):��������ǻҶȼ�,�������ʾͼ���иûҶȼ����ֵĸ���(Ƶ��)��
һάֱ��ͼ�Ľṹ��ʾΪ:
N
(
P
)
=
[
n
1
,
n
2
,
��
,
n
L
?
1
]
N
=
��
i
=
0
L
?
1
n
i
,
p
i
=
n
i
N
N(P)=[n_1,n_2,\dots,n_{L-1}] \\ N=\sum_{i=0}^{L-1}n_i,p_i=\frac{n_i}{N}
N(P)=[n1?,n2?,��,nL?1?]N=i=0��L?1?ni?,pi?=Nni??
����,LΪ�Ҷȼ��ĸ���,
n
i
n_i
ni?Ϊÿ���Ҷȵ����ظ���,��Ƶ��Ϊ
p
i
p_i
pi?��
ֱ��ͼ���⻯
ֱ��ͼ���⻯��Ҫ�����عⲻ�����ع���ȵ�ͼ��,�������ͼƬ�ĶԱȶȡ�
�㷨����:
-
����ͼ��Ҷ�ֱ��ͼ��
-
�����ۻ��ֲ����� P ( k ) P(k) P(k):
P ( k ) = �� i = 0 k p i P(k)=\sum_{i=0}^k p_i P(k)=i=0��k?pi? -
�����µĻҶȺ;ɵĻҶȵĶ�Ӧ��ϵ����:
T ( i ) = P ( i ) ? L T(i)=P(i)*L T(i)=P(i)?L
���� T ( i ) T(i) T(i)��ʾ�»Ҷ�ֵ�� -
���µĻҶ�ֵ����ɵĻҶ�ֵ��
ͼ�α任

-
ƽ��
���ɶ�Ϊ2.
x �� = [ I t ] x o r x �� = [ I t 0 T 1 ] x \bold{x}'= \begin{bmatrix}\bold{I} & \bold{t} \end{bmatrix} \bold{x} \quad or \quad \bold{x}'= \begin{bmatrix}\bold{I} & \bold{t} \\ \bold{0}^T & 1\end{bmatrix} \bold{x} x��=[I?t?]xorx��=[I0T?t1?]x -
�����˶�(��ת+ƽ��)
���ɶ�Ϊ3��
x �� = [ R t ] x \bold{x}'= \begin{bmatrix}\bold{R} & \bold{t} \end{bmatrix} \bold{x} x��=[R?t?]x
����
R = [ cos ? �� ? sin ? �� sin ? �� cos ? �� ] \bold{R}=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} R=[cos��sin��??sin��cos��?] -
���Ʊ任(������ת+ƽ��)
���ɶ�Ϊ4.
x �� = [ s R t ] x = [ a ? b t x b a t y ] x \bold{x}'= \begin{bmatrix}s\bold{R} & \bold{t} \end{bmatrix} \bold{x}= \begin{bmatrix}a & -b & t_x \\ b & a & t_y \end{bmatrix} \bold{x} x��=[sR?t?]x=[ab??ba?tx?ty??]x -
����任
���ɶ�Ϊ6,����任���ƽ������Ȼ����ƽ�С�
x �� = A x = [ a 00 a 01 a 02 a 10 a 11 a 12 ] x \bold{x}'= \bold{A} \bold{x}= \begin{bmatrix}a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \end{bmatrix} \bold{x} x��=Ax=[a00?a10??a01?a11??a02?a12??]x// ����Point2f[] srcPts��dstPts�������任����,warp_matΪ2x3�ľ��� Mat warp_mat = getAffineTransform(srcPts, dstPts); // ��ͼ����з���任 Mat warp_dst = Mat::zeros(src.rows, src.cols, src.type()); // ����ͼ�����ͼ����任�������ͼ��ijߴ� warpAffine(src, warp_dst, warp_mat, warp_dst.size()); -
��/��Ӧ�Ա任
���ɶ�Ϊ8.
x 3 �� 1 �� = H 3 �� 3 x 3 �� 1 \bold{x}'_{3\times1}= \bold{H}_{3\times3} \bold{x}_{3\times1} x3��1��?=H3��3?x3��1?
������� x 3 �� 1 �� \bold{x}'_{3\times1} x3��1��?���뾭����һ���Եõ����������,��
x �� = h 00 x + h 01 y + h 02 h 20 x + h 21 y + h 22 , y �� = h 10 x + h 11 y + h 12 h 20 x + h 21 y + h 22 x'=\frac{h_{00}x+h_{01}y+h_{02}}{h_{20}x+h_{21}y+h_{22}},\quad y'=\frac{h_{10}x+h_{11}y+h_{12}}{h_{20}x+h_{21}y+h_{22}} x��=h20?x+h21?y+h22?h00?x+h01?y+h02??,y��=h20?x+h21?y+h22?h10?x+h11?y+h12??
��Ӧ�Ա任������ֱ�ߡ�
ģ��ƥ��
ƥ�䷽����ƽ����TM_SQDIFF����һ��ƽ����TM_SQDIFF_NORMED�������TM_CCORR����һ�������TM_CCORR_NORMED��Э����TM_CCOEFF����һ��Э����TM_CCOEFF_NORMED��
// ����ͼ��I��ģ��T��ƥ����R��ƥ�䷽��������ͼ��M
matchTemplate(img, temp1, result, match_method=TM_SQDIFF, mask);
// ��λ���R�е�������Сֵ
double minVal; double maxVal; Point minLoc; Point maxLoc;
minMaxLoc(result, &minVal, &maxVal, &minLoc, &maxLoc, Mat());
// ����ƽ��������ƥ����R����Сֵ,���������������ƥ����R�����ֵ
Point matchLoc;
if (match_method == TM_SQDIFF || match_method == TM_SQDIFF_NORMED) {
matchLoc = minLoc;
} else {
matchLoc = maxLoc;
}
ͼ���˲��ͱ任

��ͨ�˲�
��ͨ�˲���(HPF)�Ǽ��ͼ���ij������,Ȼ�������������Χ���ص����Ȳ�ֵ�����������ص����ȵ��˲�����������ȱ仯�ܴ�,�������ص����Ȼ�����,��֮�ᡣ��Ҫ���ڱ�Ե��⡣
# ��ͨ�˲���
kernel_3x3 = np.array([[-1,-1,-1],[-1,8,-1],[-1,-1,-1]])
# ��������
k3 = ndimage.convolve(img, kernel_3x3)
��Ե���
�ݶ�����
-
Sobel����
G x = [ ? 1 0 + 1 ? 2 0 + 2 ? 1 0 + 1 ] ? I , G y = [ ? 1 ? 2 ? 1 0 0 0 + 1 + 2 + 1 ] ? I �� �� �� �� �� ģ G = G x 2 + G y 2 �� �� �� �� �� = a r c t a n ( G y G x ) G_{x} = \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{bmatrix} * I, G_{y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix} * I \\ �ݶ�������ģG=\sqrt{G_x^2+G_y^2}\\ �ݶȷ���\theta=arctan(\frac{G_y}{G_x}) Gx?=????1?2?1?000?+1+2+1?????I,Gy?=????10+1??20+2??10+1?????I����������ģG=Gx2?+Gy2??����������=arctan(Gx?Gy??)Mat grad_x, grad_y; int ddepth = CV_16S; int ksize = 3; double scale = 1; double delta = 0; // ����ͼ�����ͼ�����ͼ�����ȡ�x�������Ľ�����y�������Ľ������˳ߴ硢... Sobel(src_gray, grad_x, ddepth, 1, 0, ksize, scale, delta, BORDER_DEFAULT); // x�����ݶ� Sobel(src_gray, grad_y, ddepth, 0, 1, ksize, scale, delta, BORDER_DEFAULT); // y�����ݶ� // �����ת��ΪCV_8Uͼ�� Mat abs_grad_x, abs_grad_y; convertScaleAbs(grad_x, abs_grad_x); convertScaleAbs(grad_y, abs_grad_y); // �ϲ��ݶ�:��x��y������ݶȽ��м�Ȩ Mat grad; addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad); imshow("sobel gradient", grad); -
Laplace����
������˹������һ�ֶ���������,���,��һ���ö����ַ��� ? 2 f ?^2f ?2f����ʾ���䳣�õ���غ���:
h 1 = [ 0 ? 1 0 ? 1 4 ? 1 0 ? 1 0 ] , h 2 = [ ? 1 ? 1 ? 1 ? 1 8 ? 1 ? 1 ? 1 ? 1 ] h_1=\left[\begin{array}{ccc} 0&-1&0\\ -1&4&-1 \\ 0&-1&0\end{array} \right],h_2=\left[\begin{array}{ccc} -1&-1&-1\\ -1&8&-1 \\ -1&-1&-1\end{array} \right] h1?=???0?10??14?1?0?10????,h2?=????1?1?1??18?1??1?1?1????Mat dst, abs_dst; // ���롢��������ͼ�����(ӦΪCV_16S��ֹ���)���˳ߴ硢... Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT ); // �����ת��ΪCV_8U convertScaleAbs(dst, abs_dst); imshow("Laplace gradient", abs_dst);
Canny��Ե
Canny��Ե����㷨�dz�����,����Ҳ����Ȥ,����5������,��ʹ�ø�˹�˲�����ͼ�����ȥ��,�����ݶ�,�ڱ�Ե��ʹ�÷��������,�ڼ��ı�Ե��ʹ��˫��ֵȥ��������,���������еı�Ե����֮�������,�Ա��������ı�Ե�����������Եı�Ե��
�㷨����
-
ʹ�ø�˹�˲�ȥ��:
K = 1 159 [ 2 4 5 4 2 4 9 12 9 4 5 12 15 12 5 4 9 12 9 4 2 4 5 4 2 ] K = \dfrac{1}{159}\begin{bmatrix} 2 & 4 & 5 & 4 & 2 \\ 4 & 9 & 12 & 9 & 4 \\ 5 & 12 & 15 & 12 & 5 \\ 4 & 9 & 12 & 9 & 4 \\ 2 & 4 & 5 & 4 & 2 \end{bmatrix} K=1591????????24542?491294?51215125?491294?24542???????? -
ʹ��Sobel���Ӽ����ݶ�,�ݶȷ�����ɢ��Ϊ4������
-
�����ֵ����,��������졣
-
˫��ֵ:�������ݶȴ����Ͻ�,��Ϊ������Ϊ��Ե;�������ݶ�С���½�,��ȥ��;�������ݶ�λ���м�,����������غ�һ���ݶȴ����Ͻ����������ʱ,����Ϊ������Ϊ��Ե�����½��ͨ��Ϊ2:1��3:1��
cv2.Canny�������ֲ�������:
- ��һ����������Ҫ������ԭͼ��,��ͼ������ǵ�ͨ���ĻҶ�ͼ;
- �ڶ�����������ֵ1��
- ��������������ֵ2.
���нϴ����ֵ2���ڼ��ͼ�������Եı�Ե,����һ������¼���Ч��������ô����,��Ե�������Ƕ϶������ġ�������ʱ���С�ĵ�һ����ֵ���ڽ���Щ�����ı�Ե����������
Mat img_gray, canny_output;
// ���롢���(��ֵ��Cannyͼ��)���½硢�Ͻ硢Sobel���ӵĺ˳ߴ�
Canny(img_gray, canny_output, lowThresh, highThresh, kernel_size);
������ȡ
����ȡ��Canny��Ե��,����ͨ��findContours������һ����ȡͼ�������,����ǩ������:
/*
image: ��ͨ������ͼ��,ͨ���þ���Canny��Laplace�ȱ�Ե������Ӵ������Ķ�ֵ��ͼ��
contours: ��һ����������,������ÿ��Ԫ�ش�����һ��Point�㼯���ɵ�һ������
hierarchy: Ҳ��һ������,��Ԫ�غ�contours�ڵ�����һһ��Ӧ,���ڲ���4��intֵ�ֱ��ʾ�����ĺ�һ��������ǰһ������������������Ƕ������������
mode: �����ļ���ģʽ,����:
CV_RETR_EXTERNAL ֻ�������Χ����
CV_RETR_LIST �����������,���Ǽ��������������ȼ���ϵ(û�и�����Ƕ����),�˴˶���
CV_RETR_CCOMP �����������,��������ֻ���������ȼ���ϵ,��ΧΪ���㡣
CV_RETR_TREE �����������,����һ���ȼ����ṹ,������������ڲ�������
method: �������Ʒ���,����:
CV_CHAIN_APPROX_NONE ��������߽�������������������
CV_CHAIN_APPROX_SIMPLW �����������Ĺյ���Ϣ
offset: ����������Ϣ�����ԭͼ��Ӧ���ƫ����,�൱�����������ϼ�һ��ƫ��
*/
findContours(InputOutputArray image, vector<vector<Point>> contours, vector<Vec4i> hierarchy,
int mode, int method, Point offset=Point());
// ʵ������
Canny(img_gray, img_canny, 100, 250);
vector<vector<Point>> contours;
vector<Vec4i> hierarchy;
findContours(img_canny, contours, hierarchy, RETR_TREE, CHAIN_APPORX_SIMPLE);
// ��������
Mat drawing = Mat::zeros(canny_output.size(), CV_8UC3);
for (size_t i = 0; i < contours.size(); i++) {
Scalar color = Scalar(rng.uniform(0, 256), rng.uniform(0, 256), rng.uniform(0, 256));
drawContours(drawing, contours, (int)i, color, 2, 8, hierarchy, 0);
}
��ͨ�˲�
��ͨ�˲���(LPF)������������Χ���ص����Ȳ�ֵС��һ������ֵ,ƽ�������ص����ȡ�����Ҫ����ȥ���ģ����,����˵,��˹ģ������õ�ģ���˲���(ƽ���˲���)֮һ,����������Ƶ�ź�ǿ�ȵĵ�ͨ�˲�����
- �����˲�
g = f ? h , h = �� [ 1 1 1 ? 1 1 1 1 ? 1 ? ? ? ? ? 1 1 1 ? 1 ] , �� = { 1 S U M ( h ) , normalize=true 1 , normalize=false g=f\otimes h,h=\alpha \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & 1 & 1 & \cdots & 1 \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & 1 & 1 & \cdots & 1 \end{bmatrix} ,\alpha = \begin{cases} \frac{1}{SUM(h)}, & \text{normalize=true} \\ 1, & \text{normalize=false} \\ \end{cases} g=f?h,h=��?????11?1?11?1?11?1??????11?1??????,��={SUM(h)1?,1,?normalize=truenormalize=false?
��normalize=trueʱ�����˲���Ϊ��ֵ�˲���
// ����ͼ�����ͼ���˲����ߴ硢anchor��λ��(Ĭ��Ϊ������)
blur(src, dst, Size(i, i), Point(-1, -1));
- ��ֵ�˲�
// ���롢������˳ߴ�
medianBlur(src, dst, i);
- ��˹�˲�
G 0 ( x , y ) = A e ? ( x ? �� x ) 2 2 �� x 2 + ? ( y ? �� y ) 2 2 �� y 2 G_{0}(x, y) = A e^{ \dfrac{ -(x - \mu_{x})^{2} }{ 2\sigma^{2}_{x} } + \dfrac{ -(y - \mu_{y})^{2} }{ 2\sigma^{2}_{y} } } G0?(x,y)=Ae2��x2??(x?��x?)2?+2��y2??(y?��y?)2?
��õ�3x3��˹�˲���Ϊ:
[
0.0625
0.125
0.0625
0.125
0.25
0.125
0.0625
0.125
0.0625
]
\left[\begin{array}{ccc} 0.0625&0.125&0.0625\\ 0.125&0.25&0.125 \\ 0.0625&0.125&0.0625\end{array}\right]
???0.06250.1250.0625?0.1250.250.125?0.06250.1250.0625????
// ���롢������˳ߴ硢X����ĸ�˹�˱��Y����ı���
GaussianBlur(src, dst, Size(i, i), 0, 0);
-
����(���ֵ�˲�)
g ( i , j ) = m a x k , l f ( i , j ) g(i,j)=max_{k,l}f(i,j) g(i,j)=maxk,l?f(i,j)// ���νṹԪ���ṹԪ�ߴ硢anchorλ�� Mat element = getStructuringElement(MORPH_RECT, Size(3, 3), Point(-1, -1)); // ���롢������ṹԪ dilate(src, dst, element); -
��ʴ(��Сֵ�˲�)
g ( i , j ) = m i n k , l f ( i , j ) g(i,j)=min_{k,l}f(i,j) g(i,j)=mink,l?f(i,j)// ʮ�ֽṹԪ���ṹԪ�ߴ硢anchorλ�� Mat element = getStructuringElement(MORPH_CROSS, Size(3, 3), Point(-1, -1)); // ���롢������ṹԪ erode(src, dst, element); -
˫���˲�
���ڱ���ȥ��,�����ա������������������������ֵ�ļ�Ȩ���
g ( i , j ) = �� k , l f ( k , l ) w ( i , j , k , l ) �� k , l w ( i , j , k , l ) g(i,j)=\frac{\sum_{k,l}f(k,l)w(i,j,k,l)}{\sum_{k,l}w(i,j,k,l)} g(i,j)=��k,l?w(i,j,k,l)��k,l?f(k,l)w(i,j,k,l)?
����,
w ( i , j , k , l ) = d ( i , j , k , l ) ? r ( i , j , k , l ) = exp ? ( ? ( i ? k ) 2 + ( j ? l ) 2 2 �� d 2 ) ? exp ? ( ? �� f ( i , j ) ? f ( k , l ) �� 2 2 �� r 2 ) w(i,j,k,l)=d(i,j,k,l)\cdot r(i,j,k,l)=\exp\left(-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2}\right)\cdot \exp\left(-\frac{\|f(i,j)-f(k,l)\|^2}{2\sigma_r^2}\right) w(i,j,k,l)=d(i,j,k,l)?r(i,j,k,l)=exp(?2��d2?(i?k)2+(j?l)2?)?exp(?2��r2?��f(i,j)?f(k,l)��2?)
��̬ѧ����
-
������
������������(���)
o p e n ( s r c ) = d i l a t e ( e r o d e ( s r c ) ) open(src)=dilate(erode(src)) open(src)=dilate(erode(src)) -
�ղ���
��������С�ĺڶ�
d s t = c l o s e ( s r c , e l e m e n t ) = e r o d e ( d i l a t e ( s r c , e l e m e n t ) ) dst = close( src, element ) = erode( dilate( src, element ) ) dst=close(src,element)=erode(dilate(src,element)) -
��̬ѧ�ݶ�
�Զ�ֵͼ�������һ�������Խ��ſ�(blob)�ı�Եͻ�����������ǿ�������̬ѧ�ݶ�����������ı�Ե������
m o r p h g r a d ( s r c ) = d i l a t e ( s r c ) ? e r o d e ( s r c ) morphgrad(src)=dilate(src)-erode(src) morphgrad(src)=dilate(src)?erode(src)
����ʵ��
// operationΪ��̬ѧ����,����:
// ��=MORPH_OPEN,��=MORPH_CLOSE,�ݶ�=MORPH_GRADIENT
morphologyEx(src, dst, operation, element);
ͼ�������
-
��˹������(����ͼ���²���)
�²���:��˹�˲�,Ȼ���Ƴ�ͼ���ż���к���(ȡ1/4)���ϲ���:��ͼ����ÿ����������Ϊԭ����2��,������ֵ��0���;ʹ����ǰͬ���ĺ�(����4)��Ŵ���ͼ�����,��á���ֵ���ء��Ľ���ֵ��
// ���롢���������ߴ� pyrDown( src, src, Size( src.cols/2, src.rows/2 ) ); pyrUp(src, src, Size(src.cols*2, src.rows*2)); -
������˹������(�����²�ͼ����ؽ��ϲ���)
Ϊʹ�ϲ������²�������,������˹����������Ϊ:
L i = G i ? P y r U p ( P y r D o w n ( G i ) ) = G i ? U p ( P y r D o w n ( G i ) ) ? H 5 �� 5 L_i=G_i-PyrUp(PyrDown(G_i))=G_i-Up(PyrDown(G_i))\otimes H_{5\times 5} Li?=Gi??PyrUp(PyrDown(Gi?))=Gi??Up(PyrDown(Gi?))?H5��5?
����Up�����ǽ�Դͼ����λ��Ϊ(x,y)������ӳ�䵽Ŀ��ͼ���(2x+1,2y+1)λ��, H 5 �� 5 H_{5��5} H5��5?��ʾ5x5�ĸ�˹�ˡ�
Mat src; // ԭͼ
Mat laplace_pyramid, temp; // ������ͼ���ݴ�ԭͼ
pyrDown(src, src, Size(src.cols / 2, src.rows / 2));
pyrUp(src, src, Size(src.cols * 2, src.rows * 2));
laplace_pyr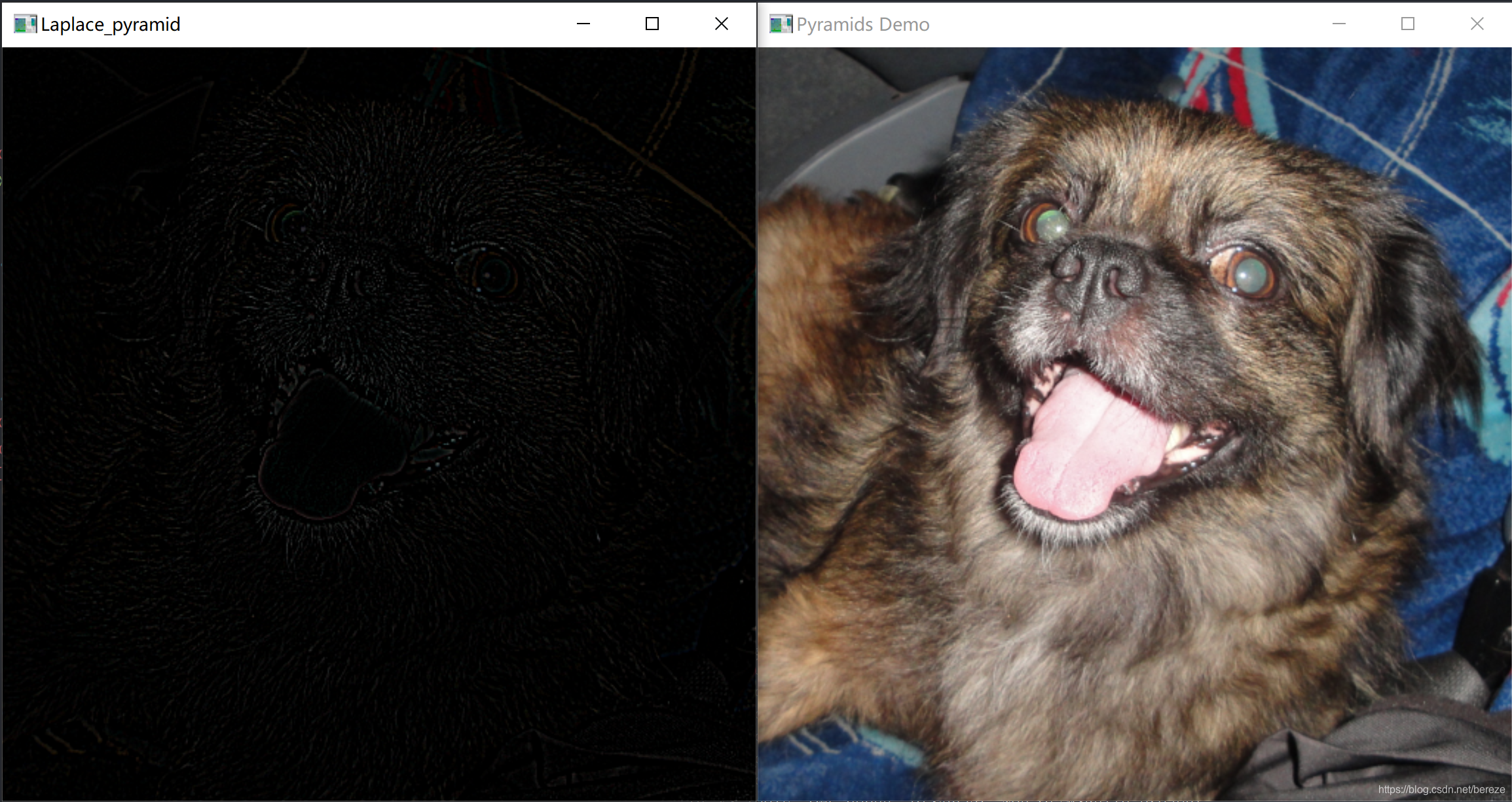
amid = temp - src;
imshow("Laplace_pyramid", laplace_pyramid);

Hough�任
Hough�任���ڼ��ֱ��,��ʹ��ǰ��Ҫ�Ⱦ�����Ե����Ԥ������
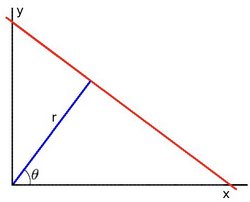
����һ��ֱ��,����ʹ�ü�������ʽ����:
y
=
(
?
cos
?
��
sin
?
��
)
x
+
(
r
sin
?
��
)
y = (-\frac{\cos \theta}{\sin \theta})x+(\frac{r}{\sin \theta})
y=(?sin��cos��?)x+(sin��r?)
-
����ÿ���� ( x 0 , y 0 ) (x_0,y_0) (x0?,y0?),���Զ��崩���õ��ֱ�ߴ�:
r �� = x 0 cos ? �� + y 0 sin ? �� r_{\theta}=x_0\cos\theta+y_0\sin\theta r��?=x0?cos��+y0?sin��
һ�� ( r �� , �� ) (r_{\theta},\theta) (r��?,��)�ʹ���һ������ ( x 0 , y 0 ) (x_0,y_0) (x0?,y0?)��ֱ�ߡ� -
���ڸ�����һ���� ( x 0 , y 0 ) (x_0,y_0) (x0?,y0?),���Ի��� ( r , �� ) (r,\theta) (r,��)������,��Ϊһ����������:(ֻ���� r > 0 r>0 r>0�� 0 < �� < 2 �� 0<\theta<2\pi 0<��<2��)

-
���Ƕ�ͼ���е����е㶼�������������ߡ����������ͬ��������ཻ��һ�� ( r , �� ) (r,\theta) (r,��),������������㶼������ֱ���ϡ�

-
�ɴ�,���Զ���һ��������ֵ�����һ��ֱ��,�����������������ֵʱ,�����ý��� ( r , �� ) (r,\theta) (r,��)��������һ��ֱ�ߡ������Hough�߱任��
// ԭͼ����Ե�������Ķ�ֵ��ͼ����Hough�任�����������Hough�任�����
Mat src, img_canny, cdst, cdst_p;
// step 1��Ե���Ԥ����
Canny(src, img_canny, 50, 200, 3);
// ����Եͼ���ΪBGRͼ��,�Ա������ӻ�
cvtColor(img_canny, cdst, COLOR_GRAY2BGR);
cdst_p = cdst.clone();
// step 2 Standard Hough line transform
vector<Vec2f> lines; // �洢����ֱ�ߵ�����,����ÿ��Ԫ�ر�ʾһ��ֱ��(rho, theta)
// ����ͼ��ֱ��������������Ϊ��λ�ľ��뾫�ȡ��Ի���Ϊ��λ�ĽǶȾ��ȡ������ֵ��(...)
HoughLines(img_canny, lines, 1, CV_PI/180, 150, 0, 0);
// Draw the lines
for (size_t i = 0; i < lines.size(); i++) {
float rho = lines[i][0], theta = lines[i][1];
Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a * rho, y0 = b * rho;
pt1.x = cvRound(x0 + 1000 * (-b));
pt1.y = cvRound(y0 + 1000 * a);
pt2.x = cvRound(x0 + 1000 * b);
pt2.y = cvRound(y0 + 1000 * (-a));
line(cdst, pt1, pt2, Scalar(0, 0, 255), 3, LINE_AA);
}
// step 3 Probabilistic Hough transform �ۼƸ��ʻ���任(��ȱ�����任Ч������)
vector<Vec4i> lines_p; // ÿ��ֱ�����ĸ�intֵ(x1, y1, x2, y2)��ʾ,(x1, y1)��(x2, y2)Ϊ�߶εĶ˵�
// ����ͼ��ֱ�����������뾫�ȡ��ǶȾ��ȡ������ֵ������߶γ��ȡ�ͬһֱ��������֮��������
HoughLinesP(img_canny, lines_p, 1, CV_PI/180, 50, 50, 10);
// Draw the lines
for (size_t i = 0; i < lines_p.size(); i++) {
Vec4i l = lines_p[i];
line(cdst_p, Point(l[0], l[1]), Point(l[2],l[3]), Scalar(0, 0, 255), 3, LINE_AA);
}
// Show results
imshow("Source", src);
imshow("Detected Lines (in red) - Standard", cdst);
imshow("Detected Lines (in red) - Probabilistic", cdst_p);

�����ֹ�����
Harris�ǵ�
Harris�ǵ������ת������,�������г߶Ȳ����ԡ�
����˼��
ʹ��һ���̶�������ͼ���Ͻ������ⷽ���ϵĻ���,�Ƚϻ���ǰ�������ػҶȱ仯,����������ⷽ���ϵĻ���,ʹ�ûҶȱ仯���ϴ�,����Ϊ�ô����д��ڽǵ㡣
�㷨����
-
����ͼ�� I ( x , y ) I(x,y) I(x,y)�� x x x�� y y y�����ϵ��ݶ� I x , I y I_x,I_y Ix?,Iy?:
I x = ? I ? x = I �� [ ? 1 0 1 ] I y = ? I ? y = I �� [ ? 1 0 1 ] T I_x=\frac{?I}{?x}=I��\begin{bmatrix} -1 & 0 & 1 \end{bmatrix} \\ I_y=\frac{?I}{?y}=I��\begin{bmatrix} -1 & 0 & 1 \end{bmatrix}^T Ix?=?x?I?=I��[?1?0?1?]Iy?=?y?I?=I��[?1?0?1?]T -
����ͼ�����������ݶȵij˻�:
I x 2 = I x ? I x I y 2 = I y ? I y I x I y = I x ? I y I_x^2 =I_x*I_x \\ I_y^2 =I_y*I_y \\ I_xI_y =I_x*I_y Ix2?=Ix??Ix?Iy2?=Iy??Iy?Ix?Iy?=Ix??Iy? -
ʹ�ø�˹������ I x 2 I_x^2 Ix2?�� I y 2 I_y^2 Iy2?�� I x I y I_xI_y Ix?Iy?���и�˹��Ȩ(ȡ �� = 2 ��=2 ��=2, k s i z e = 3 ksize=3 ksize=3),�������ĵ�Ϊ ( x , y ) (x,y) (x,y)�Ĵ��� W W W��Ӧ�ľ��� M M M:
A = �� ( x , y ) � W g ( I x 2 ) = �� ( x , y ) � W I x 2 ? w ( x , y ) B = �� ( x , y ) � W g ( I y 2 ) = �� ( x , y ) � W I y 2 ? w ( x , y ) C = �� ( x , y ) � W g ( I x I y ) = �� ( x , y ) � W I x I y ? w ( x , y ) A=\sum\limits_{(x,y)�W}g(I_x^2)=\sum\limits_{(x,y)�W}I_x^2*w(x,y)\\ B=\sum\limits_{(x,y)�W}g(I_y^2)=\sum\limits_{(x,y)�W}I_y^2*w(x,y)\\ C=\sum\limits_{(x,y)�W}g(I_xI_y)=\sum\limits_{(x,y)�W}I_xI_y*w(x,y)\\ A=(x,y)�W��?g(Ix2?)=(x,y)�W��?Ix2??w(x,y)B=(x,y)�W��?g(Iy2?)=(x,y)�W��?Iy2??w(x,y)C=(x,y)�W��?g(Ix?Iy?)=(x,y)�W��?Ix?Iy??w(x,y)
���� M = [ A C C B ] = �� ( x , y ) � W w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] M=\begin{bmatrix} A & C \\C & B\end{bmatrix}=\sum\limits_{(x,y)�W}w(x,y)\begin{bmatrix} I_x^2 & I_xIy \\I_xI_y & I_y^2\end{bmatrix} M=[AC?CB?]=(x,y)�W��?w(x,y)[Ix2?Ix?Iy??Ix?IyIy2??], w ( x , y ) w(x,y) w(x,y)��ʾ��˹�������ڡ� -
����ÿ�����ص� ( x , y ) (x,y) (x,y)����Harris��Ӧֵ R R R:
R = d e t ( M ) ? k ( t r a c e ( M ) ) 2 d e t ( M ) = �� 1 �� 2 t r a c e ( M ) = �� 1 + �� 2 R=det(M)-k(trace(M))^2 \\ det(M)=��_1��_2 \\ trace(M)=��_1+��_2 R=det(M)?k(trace(M))2det(M)=��1?��2?trace(M)=��1?+��2?
���� �� 1 , �� 2 ��_1,��_2 ��1?,��2?�Ǿ��� M M M��2������ֵ, k k k��һ��ָ��ֵ,����һ���������,��Ҫʵ��ȷ�����ĺ��ʴ�С,ͨ������ֵ��0.04��0.06֮��,���Ĵ���ֻ�ǵ��ں�������״���ѡ�R R Rȡ���� M M M������ֵ,���ڽǵ� �O R �O |R| �OR�O�ܴ�,ƽ̹������ �O R �O |R| �OR�O��С,��Ե�� R R RΪ��ֵ��
-
�˳�С����ֵ t t t�� R R Rֵ:
R = { R : d e t ( M ) ? k ( t r a c e ( M ) ) 2 > t } R=\{R:det(M)-k(trace(M))^2 \gt t \} R={R:det(M)?k(trace(M))2>t}
�����3��3����5��5��������з����ֵ����,��ֲ����ֵ�㼴Ϊͼ���еĽǵ㡣
����ʵ��
Mat dst = Mat::zeros(src.size(), CV_32FC1); // ���ͼ��(�洢�ǵ���ӦR)
int block_size = 2; // ���ڴ�С
int aperture_size = 3; // �����ݶ�ʱSobel���ӵĺ˳ߴ�
double k = 0.04; // �ǵ���Ӧ�����е�kֵ,����k��ֵ����ٱ����ǵ������
cornerHarris(src_gray, dst, block_size, aperture_size, k);
Mat dst_norm, dst_norm_scaled;
// ���ǵ���Ӧ��һ����[0, 255]
normalize(dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat());
// ת��Ϊ��ͨ��CV_8UC1
converScaleAbs(dst_norm, dst_norm_scaled);
// ����������ֵ�����Ľǵ�
int thresh = 200;
for (int i = 0; i < dst_norm.rows; i++) {
for (int j = 0; j < dst_norm.cols; j++) {
if ((int) dst_norm.at<float>(i,j) > thresh) {
circle(dst_norm_scaled, Point(j, i), 5, Scalar(0), 2, 8, 0);
}
}
}
imshow("harris corner", dst_norm_scaled);

Shi-Tomasi�ǵ�(GFFT)
Shi-Tomasi�ǵ���ԭ����Harris�ǵ�����ͬ,ֻ��������б�ʽ��ѡȡ�ϲ�ͬ,Shi-Tomasi�ǵ���ѡȡ�����е���С���Ǹ����б𡣼��ǵ���Ӧ��Ϊ
R
=
min
?
(
��
1
,
��
2
)
R=\min(\lambda_1,\lambda_2)
R=min(��1?,��2?)
vector<Point2f> corners; // �ǵ�����,ÿ��Ԫ��Ϊһ���ǵ�
int max_corners = 23; // ���Ľǵ���Ŀ���ֵ,���и���Ľǵ�,����Ӧֵ���
double quality_level = 0.01; // �ɽ��ܵ���С��Ӧֵ,����Ӧ���ֵΪ1500,quality_level=0.01,��С��15����Ӧ�����ܾ�
double min_distance = 10; // �ǵ�֮�����Сŷʽ����
int block_size = 3, gradient_size = 3; // ����M����Ĵ��ڴ�С���ݶ����ӵĺ˳ߴ�
bool use_harris_detector = false; // �Ƿ�ʹ��harris�ǵ�����
double k = 0.04; // harris�ǵ����kֵ
goodFeaturesToTrack(src_gray,
corners,
max_corners,
quality_level,
min_distance,
Mat(), // ROI mask
block_size,
gradient_size,
use_harris_detector,
k);
// ���ƽǵ�
for (size_t i = 0; i < corners.size(); i++) {
circle(src, corners[i], 3, Scalar(0,0,255), FILLED);
}
imshow("Image", src);

SIFT����
SIFT������ת���߶ȡ����Ȳ����ԡ�
����˼��
�߶Ȳ��������任(Scale-Invariant Feature Transform),ʹ��DoG(��ָ�˹)����ȡ������,DoG���ò�ͬ�ij߶ȿռ�����(��˹�ֲ��ı��� �� \sigma ��)��ͼ�����ƽ��,Ȼ��Ƚ�ƽ����ͼ�������,��������ؾͿ����������㡣�Եõ�������������,��һЩ���õ�,SIFT���ӻ��ʣ�µ�ÿ����������һ��128ά����������������
�㷨����
-
DoG�߶ȿռ�ļ�ֵ���:
���ȹ���DoG�߶ȿռ�,��SIFT��ʹ�ò�ͬ�����ĸ�˹ģ������ʾ��ͬ�ij߶ȿռ䡣������߶ȿռ���Ϊ�˼���ڲ�ͬ�߶��¶����ڵ�������,������ļ��ʹ��DoG(���ò�ִ�����)�����Ƽ���LoG(ͼ��Ķ�����)�� -
ɾ�����ȶ��ļ�ֵ��:
��Ҫɾ������:�ͶԱȶȵļ�ֵ��Ͳ��ȶ��ı�Ե��Ӧ�㡣
-
ȷ���������������:
�������������Ϊ���ġ��� 3 �� 1.5 �� 3\times1.5\sigma 3��1.5��Ϊ�뾶�������ڼ���������ص���ݶȵķ�ֵ�ͷ���,Ȼ��ʹ��ֱ��ͼ���ݶȵķ��ǽ���ͳ�ơ�ֱ��ͼ�ĺ���Ϊ�ݶȵķ���,����Ϊ�ݶȷ����Ӧ�ݶȷ�ֵ���ۺ�,ֱ��ͼ�е���߷�����Ӧ�ķ���Ϊ�������������
-
�����������������
���Ƚ���������תΪ������ķ���,��������Ϊ���ĵ� 16 �� 16 16\times16 16��16���ڵ����ص��ݶȷ�ֵ�ͷ���,�������ڵ����طֳ� 4 �� 4 4\times4 4��4�Ŀ�,ÿ�������ڲ�16�����ص�8�������ֱ��ͼͳ��,����һ��������,���γ� 4 �� 4 �� 8 = 128 4\times4\times8=128 4��4��8=128ά������������

����ʵ��
int numFeatures = 400; // ��ȡ����������Ŀ
Ptr<SIFT> detector = SIFT::create(numFeatures);
// step 1 detect the keypoints
vector<KeyPoint> keypoints;
detector->detect(src_gray, keypoints);
// draw keypoints
Mat img_keypoints;
drawKeypoints(src, keypoints, img_keypoints);
// show detected keypoints
imshow("SIFT", img_keypoints);
waitKey(0);
// detect the keypoints and descriptors
vector<KeyPoint> kp1, kp2;
Mat desc1, desc2;
detector->detectAndCompute(img1, Mat(), kp1, desc1);
detector->detectAndCompute(img2, Mat(), kp2, desc2);
// match,ʹ��flann����ƥ��
vector<vector<DMatch>> nn_matches;
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create(DescriptorMatcher::FLANNBASED);
matcher->knnMatch(desc1, desc2, nn_matches, 2);
// ѡ��õ�ƥ��
const float match_ratio = 0.8f;
vector<DMatch> good_matches;
for (size_t i = 0; i < nn_matches.size(); i++) {
if (nn_matches[i][0].distance < match_ratio * nn_matches[i][1].distance) {
good_matches.push_back(nn_matches[i][0]);
}
}
ORB����
����ԭ��
ORB�㷨��FAST������ļ�ⷽ����BRIEF���������ӽ������,�����иĽ����Ż���
�㷨����
-
����FAST���������,Ȼ������Harris�ǵ�Ķ�������,��FAST����������ѡ��Harris�ǵ���Ӧֵ����N�������㡣������Ӧ����Ϊ
R = d e t ( M ) ? k ( t r a c e ( M ) ) 2 R=det(M)-k(trace(M))^2 R=det(M)?k(trace(M))2
ORB����NMS��ɸѡ�ؼ���,ֻ������������ǰn���ؼ��㡣����FAST�ؼ��㲻�߱��߶Ȳ�����,���ORB������ͼ���������ʵ�ֳ߶Ȳ�����,ͨ��������˹������,Ȼ����ÿһ�������ͼ���ϼ��ǵ㡣 -
���ûҶ����ķ�ʵ��BRIEF�����ӵ���ת�����ԡ�
�Ҷ����ķ���Ϊ�ǵ�ĻҶȺ�����֮�����һ��ƫ��,��������������ڱ�ʾ����������������p,p���������صľض���Ϊ:
m i j = �� x = ? r r �� y = ? r r x i y j I ( x , y ) m_{ij}=\sum\limits_{x=-r}^{r}\sum\limits_{y=-r}^{r}x^iy^jI(x,y) mij?=x=?r��r?y=?r��r?xiyjI(x,y)
���� I ( x , y ) I(x,y) I(x,y)Ϊ�� ( x , y ) (x,y) (x,y)���ĻҶ�ֵ, q q qΪ����, i , j = 0 , 1 i,j=0,1 i,j=0,1����ô���ǿ��Եõ�ͼ�������Ϊ:
C = ( m 10 m 00 , m 01 m 00 ) C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}}) C=(m00?m10??,m00?m01??)
��ô�����������ĵļнǶ���ΪFAST������ķ���:
�� = a r c t a n ( m 01 , m 10 ) \theta=arctan(m_{01},m_{10}) ��=arctan(m01?,m10?)
BRIEF��������ͨ���Ƚ��������ص�p�����������ڵ�256�����ؼ�IJ�ֵ�����ɶ�����������,������һ������Ϊ256�Ķ�ֵ�봮,�������������ڵ�256��������,�� 2 �� 256 2\times256 2��256���� ( x i , y i ) , i = 1 , 2 , . . . . . , 2 n (x_i,y_i),i=1,2,.....,2n (xi?,yi?),i=1,2,.....,2n���һ������ S S S:
S = [ x 1 x 2 . . . x 2 n y 1 y 2 . . . y 2 n ] S=\begin{bmatrix} x_1 & x_2 & ... &x_{2n} \\ y_1 & y_2 & ... & y_{2n} \end{bmatrix} S=[x1?y1??x2?y2??......?x2n?y2n??]
ORBʹ�������� �� \theta ���Ͷ�Ӧ����ת���� R �� R_{\theta} R��?,���� S S S��У���汾 S �� S_{\theta} S��?:
S �� = R �� S S_{\theta}=R_{\theta}S S��?=R��?S
����,
R �� = [ c o s �� s i n �� ? s i n �� c o s �� ] R_{\theta}=\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix} R��?=[cos��?sin��?sin��cos��?]
�� \theta ������������õ�FAST������ķ�����������һ�����ص� x i , y i x_i,y_i xi?,yi?,�� x i < y i x_i<y_i xi?<yi?,���λ�õ�������Ϊ1,����Ϊ0��
-
rBRIEF��������ӵ������ԡ�
����ʵ��
Ptr<ORB> detector = ORB::create();
vector<KeyPoint> keypoints1, keypoints2;
Mat descriptors1, descriptors2;
// step 1: Detect the keypoints using ORB detector, compute the descriptors
detector->detectAndCompute(img_gray1, Mat(), keypoints1, descriptors1); // �ڶ�������ΪROI mask
detector->detectAndCompute(img_gray2, Mat(), keypoints2, descriptors2);
// step 2: Matching descriptor vectors with a brute force matcher
// ����ORB����������uchar���͵�,���ֻ����BFƥ�䷨
// Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
Ptr<DescriptorMatcher> matcher =
DescriptorMatcher::create(DescriptorMatcher::BRUTEFORCE_HAMMING);
// ��һƥ��
// vector<DMatch> matches;
// matcher->match(descriptors1, decriptors2, matches);
// knnƥ��,knn_matches[i]����k�Ժ�ѡƥ��
vector<vector<DMatch>> knn_matches;
matcher->knnMatch(descriptors1, decriptors2, knn_matches, 2); // ���һ������Ϊk���ڵ�kֵ
// step 3: Filter matches using the Lowe's ratio test
const float ratio_thresh = 0.7f;
vector<DMatch> good_matches;
for (size_t i = 0; i < knn_matches.size(); i++) {
// ��[i]����õ�ƥ��[i][0]С�ڵڶ��õ�ƥ��[i][1]�ľ����0.7,����Ϊ�Ǻõ�ƥ���
if (knn_matches[i][0].distance < ratio_thresh * knn_matches[i][1].distance) {
good_matches.push_back(knn_matches[i][0]);
}
}
// step 4: Draw matches
Mat img_matches;
drawMatches(img1, keypoints1, img2, keypoints2, good_matches, img_matches,
// ����Ĭ�ϲ���
Scalar::all(-1), // ƥ�����ɫ
Scalar::all(-1), // �ؼ������ɫ
vector<char>(), // ƥ������
DrawMatchesFlags::NOT_DRAW_SINGLE_POINTS);
imshow("Good matches", img_matches);
waitKey(0);
����Optical flow
�����ǿռ��˶������ڹ۲����ƽ���ϵ������˶���˲ʱ�ٶ�,������ͼ��������������ʱ�����ϵı仯������֮֡�����������ҵ���һ֡�͵�ǰ֮֡��Ķ�Ӧ��ϵ,�Ӷ����������֮֡����˶���Ϣ��һ�ַ�����
����ͨ����ͬĿ��Ĺ����˶��ٶ��ж����������ǵľ��롣һЩ��Զ��Ŀ��,����,�˶��ú���;��һЩ�Ͻ���Ŀ��,���š��˶��ýϿ졣
����Լ������
��������������������:
- �ں̵ܶ�ʱ����Ŀ�������ֵ����仯;
- �ڽ������ؾ������Ƶ��˶���
��
I
(
x
,
y
,
t
)
I(x,y,t)
I(x,y,t)��ʾtʱ�̵����ص�
(
x
,
y
)
(x,y)
(x,y)�ĻҶ�ֵ,��������Ⱥ㶨����,������:
I
(
x
,
y
,
t
)
=
I
(
x
+
��
x
,
y
+
��
y
,
t
+
��
t
)
I(x,y,t) = I(x + \Delta x, y + \Delta y, t + \Delta t)
I(x,y,t)=I(x+��x,y+��y,t+��t)
���Ƕ���ʽ�Ҳ����һ��Taylorչ��,�ɵ�:
I
(
x
+
��
x
,
y
+
��
y
,
t
+
��
t
)
��
I
(
x
,
y
,
t
)
+
?
I
?
x
��
x
+
?
I
?
y
��
y
+
?
I
?
t
��
t
I(x + \Delta x, y + \Delta y, t + \Delta t) \approx I(x,y,t) + \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t
I(x+��x,y+��y,t+��t)��I(x,y,t)+?x?I?��x+?y?I?��y+?t?I?��t
���õ�����Լ������:
?
I
?
x
��
x
+
?
I
?
y
��
y
+
?
I
?
t
��
t
=
0
\frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t = 0
?x?I?��x+?y?I?��y+?t?I?��t=0
�����������������δ֪��
(
��
x
,
��
y
)
(\Delta x,\Delta y)
(��x,��y),����û��Ψһ�⡣Ϊ�˵õ�Ψһ��,�ͱ�������Լ�������,���Ҳ�����˲�ͬ���㷨��
Lucas-Kanade�㷨
Lucas-Kanade�㷨����ֲ������㶨,��ʹ��һ��3x3��patch,patch�ڵ�9�����ض�����ͬ�����˶������,�����Ϊ��:9������,���2��δ֪�����㷨ʹ����С���˷����:
[
��
x
��
y
]
=
[
��
i
f
x
i
2
��
i
f
x
i
f
y
i
��
i
f
x
i
f
y
i
��
i
f
y
i
2
]
?
1
[
?
��
i
f
x
i
f
t
i
?
��
i
f
y
i
f
t
i
]
\begin{bmatrix} \Delta x \\ \Delta y \end{bmatrix} = \begin{bmatrix} \sum_{i}{f_{x_i}}^2 & \sum_{i}{f_{x_i} f_{y_i} } \\ \sum_{i}{f_{x_i} f_{y_i}} & \sum_{i}{f_{y_i}}^2 \end{bmatrix}^{-1} \begin{bmatrix} - \sum_{i}{f_{x_i} f_{t_i}} \\ - \sum_{i}{f_{y_i} f_{t_i}} \end{bmatrix}
[��x��y?]=[��i?fxi??2��i?fxi??fyi???��i?fxi??fyi??��i?fyi??2?]?1[?��i?fxi??fti???��i?fyi??fti???]
����
f
x
=
?
I
?
x
??
;
??
f
y
=
?
I
?
y
;
??
f
t
=
?
I
?
t
f_x = \frac{\partial I}{\partial x} \; ; \; f_y = \frac{\partial I}{\partial y}; \;f_t= \frac{\partial I}{\partial t}\\
fx?=?x?I?;fy?=?y?I?;ft?=?t?I?
ע��,ʽ�е�������Harris�ǵ����е�M����,������ǵ���ʺϸ��١�
Ϊ�˽���ϴ��˶�ʱ�����ٵ�����,�㷨ʹ��ͼ�������,��ͼ������ϲ���ʱ,���˶������С�˶�,С�˶���ȥ���ˡ�
����ʵ��
vector<Point2f> prevPts, currPts;
// ����ͼ������ǵ㡢�ǵ���Ŀ���ֵ���ǵ��������ǵ�֮�����Сŷʽ���롢ROI�����㻥��غ����Ĵ��ڳߴ硢�Ƿ�ʹ��Harris�ǵ㡢Harris�ǵ��kֵ
goodFeaturesToTrack(prevImg, prevPts, 100, 0.3, 7, Mat(), 7, false, 0.04);
vector<uchar> status;
vector<float> err;
TermCriteria criteria = TermCriteria((TermCriteria::COUNT) + (TermCriteria::EPS), 10, 0.03);
// ǰһ֡ͼ��һ֡ͼ��ǰһ֡���ٵ㡢��һ֡���ٵ㡢�Ƿ��ҵ�����(�Ƿ���ٳɹ�)�����������Ĵ��ڳߴ硢�������IJ���-1��������ֹ����
calcOpticalFlowPyrLK(prevImg, currImg, prevPts, currPts, status, err, Size(15,15), 2, criteria);
// ѡ��õ�
vector<Point2f> good_new;
for (uint i = 0; i < prevPts.size(); i++) {
if (status[i] == 1) {
good_new.push_back(currPts[i]);
// draw the tracks
line(prevImg, currPts[i], prevPts[i], color, thickness);
}
}
ͼ���ֵ
����ڲ�ֵ

��ʵ��Ӧ����,ֱ�������и���,�����и��ơ�
˫���Բ�ֵ
��֪
Q
11
(
x
1
,
y
1
)
��
Q
12
(
x
1
,
y
2
)
��
Q
21
(
x
2
,
y
1
)
��
Q
22
(
x
2
,
y
2
)
Q11(x1,y1)��Q12(x1,y2)��Q21(x2,y1)��Q22(x2,y2)
Q11(x1,y1)��Q12(x1,y2)��Q21(x2,y1)��Q22(x2,y2),�����е�P(x,y)��ֵ��

˫���Բ�ֵ�Ƿֱ���������������˹�3�ε����Բ�ֵ,��ͼ��ʾ,����x������2�ε����Բ�ֵ,���R1(x, y1)��R2(x, y2)������ʱ��,����y�������1�ε����Բ�ֵ�ó�P(x, y)(ʵ���ϵ���2����ķ�����y��xҲ��һ���Ľ��)��
-
�������ĵ��غ϶�Ӧ
s r c x = ( d s t x + 0.5 ) ? s r c w / d s t w ? 0.5 s r c y = ( d s t y + 0.5 ) ? s r c h / d s t h ? 0.5 src_x=(dst_x+0.5)*src_w/dst_w-0.5 \\src_y=(dst_y+0.5)*src_h/dst_h-0.5 srcx?=(dstx?+0.5)?srcw?/dstw??0.5srcy?=(dsty?+0.5)?srch?/dsth??0.5
���ڼ�������� s r c x , s r c y src_x, src_y srcx?,srcy?,����һ���Ǹ�����,��Ҫ�ҵ����ڽ����ĸ�ʵ�ʴ��ڵ����ص㡣
���� s r c = ( 1.2 , 3.4 ) src = (1.2, 3.4) src=(1.2,3.4),���ҵ��ڽ�����(1, 3) (2, 3) (1, 4) (2, 4), -
x�������Բ�ֵ
f ( R 1 ) = x 2 ? x x 2 ? x 1 f ( Q 11 ) + x ? x 1 x 2 ? x 1 f ( Q 21 ) f ( R 2 ) = x 2 ? x x 2 ? x 1 f ( Q 12 ) + x ? x 1 x 2 ? x 1 f ( Q 22 ) f(R_1)=\frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21}) \\ f(R_2)=\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22}) f(R1?)=x2??x1?x2??x?f(Q11?)+x2??x1?x?x1??f(Q21?)f(R2?)=x2??x1?x2??x?f(Q12?)+x2??x1?x?x1??f(Q22?) -
y�������Բ�ֵ
f ( P ) = y 2 ? y y 2 ? y 1 f ( R 1 ) + y ? y 1 y 2 ? y 1 f ( R 2 ) f(P) =\frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2) f(P)=y2??y1?y2??y?f(R1?)+y2??y1?y?y1??f(R2?)
-
����ʽ������
f ( x , y ) = ( x 2 ? x ) ( y 2 ? y ) ( x 2 ? x 1 ) ( y 2 ? y 1 ) f ( Q 11 ) + ( x ? x 1 ) ( y 2 ? y ) ( x 2 ? x 1 ) ( y 2 ? y 1 ) f ( Q 21 ) + ( x 2 ? x ) ( y ? y 1 ) ( x 2 ? x 1 ) ( y 2 ? y 1 ) f ( Q 12 ) f(x,y) =\frac{(x_2-x)(y_2-y)}{(x_2-x_1)(y_2-y_1)}f(Q_{11})+\frac{(x-x_1)(y_2-y)}{(x_2-x_1)(y_2-y_1)}f(Q_{21})+\frac{(x_2-x)(y-y_1)}{(x_2-x_1)(y_2-y_1)}f(Q_{12}) f(x,y)=(x2??x1?)(y2??y1?)(x2??x)(y2??y)?f(Q11?)+(x2??x1?)(y2??y1?)(x?x1?)(y2??y)?f(Q21?)+(x2??x1?)(y2??y1?)(x2??x)(y?y1?)?f(Q12?)���� x 2 = x 1 + 1 , y 2 = y 1 + 1 x_2=x_1+1, y_2=y_1+1 x2?=x1?+1,y2?=y1?+1,�����
f ( x , y ) = f ( Q 11 ) ( x 2 ? x ) ( y 2 ? y ) + f ( Q 21 ) ( x ? x 1 ) ( y 2 ? y ) + f ( Q 12 ) ( x 2 ? x ) ( y ? y 1 ) + f ( Q 22 ) ( x ? x 1 ) ( y ? y 1 ) \begin{aligned}f(x,y) = &f(Q_{11})(x_2-x)(y_2-y)+f(Q_{21})(x-x_1)(y_2-y)+ \\&f(Q_{12})(x_2-x)(y-y_1)+f(Q_{22})(x-x_1)(y-y_1) \end{aligned} f(x,y)=?f(Q11?)(x2??x)(y2??y)+f(Q21?)(x?x1?)(y2??y)+f(Q12?)(x2??x)(y?y1?)+f(Q22?)(x?x1?)(y?y1?)?
����궨
����
����һ��3D��
P
(
X
,
Y
,
Z
)
P(X,Y,Z)
P(X,Y,Z),���Ӧ���ͼ������Ϊ
p
(
u
,
v
)
p(u,v)
p(u,v),���Խ�������ͶӰ��ϵ:
s
[
u
v
1
]
=
[
a
r
u
0
0
b
v
0
0
0
1
]
[
r
1
r
2
r
3
t
]
[
X
Y
Z
1
]
=
K
T
P
s\left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \left[ \begin{matrix} a & r & u_0 \\ 0 & b & v_0 \\ 0 & 0 & 1 \end{matrix} \right] \begin{bmatrix} \bold{r}_1 & \bold{r}_2 & \bold{r}_3 & \bold{t} \end{bmatrix} \left[ \begin{matrix} X \\ Y \\ Z \\ 1\end{matrix} \right] = \bold{K} \bold{T} \bold{P}
s???uv1????=???a00?rb0?u0?v0?1????[r1??r2??r3??t?]?????XYZ1??????=KTP
����KΪ����ڲξ���,[R, t]Ϊ�����Ρ����������������:
{
x
d
i
s
t
o
r
t
e
d
=
x
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
+
2
p
1
x
y
+
p
2
(
r
2
+
2
x
2
)
y
d
i
s
t
o
r
t
e
d
=
y
(
1
+
k
1
r
2
+
k
2
r
4
+
k
3
r
6
)
+
p
1
(
r
2
+
2
y
2
)
+
2
p
2
x
y
\left \{ \begin{aligned}x_{distorted}=x(1+k_1r^2+k_2r_4+k_3r^6)+2p_1xy+p_2(r^2+2x^2) \\y_{distorted}=y(1+k_1r^2+k_2r_4+k_3r^6)+p_1(r^2+2y^2)+2p_2xy\end{aligned}\right.
{xdistorted?=x(1+k1?r2+k2?r4?+k3?r6)+2p1?xy+p2?(r2+2x2)ydistorted?=y(1+k1?r2+k2?r4?+k3?r6)+p1?(r2+2y2)+2p2?xy?
(x, y)Ϊ�����һ��ƽ�����ꡣ����궨��Ŀ�ľ������������Щ������
��ʽ��(�����ǻ���)
����ʹ�ñ궨�������б궨,�����������㶼����,���Լ����ƽ��ΪZ=0,�Ӷ�ȥ�� r 3 r_3 r3?,����ͶӰ��ϵ����дΪ:
s [ u v 1 ] = [ a r u 0 0 b v 0 0 0 1 ] [ r 1 r 2 t ] [ X Y 1 ] s\left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = \left[ \begin{matrix} a & r & u_0 \\ 0 & b & v_0 \\ 0 & 0 & 1 \end{matrix} \right] \begin{bmatrix} \bold{r}_1 & \bold{r}_2 & \bold{t} \end{bmatrix} \left[ \begin{matrix} X \\ Y \\ 1\end{matrix} \right] s???uv1????=???a00?rb0?u0?v0?1????[r1??r2??t?]???XY1????
�м����� K [ r 1 , r 2 , t ] \bold{K}[\bold{r}_1 , \bold{r}_2 , \bold{t}] K[r1?,r2?,t]�ʹ���3D�����ͼ�������ĵ�ӦH,�����:
H = [ h 1 h 2 h 3 ] = �� K [ r 1 r 2 t ] \bold{H}= \begin{bmatrix} \bold{h}_1 & \bold{h}_2 & \bold{h}_3 \end{bmatrix} =\lambda \bold{K} \begin{bmatrix} \bold{r}_1 & \bold{r}_2 & \bold{t} \end{bmatrix} H=[h1??h2??h3??]=��K[r1??r2??t?]
��
\lambda
��Ϊ����(��������Ϊ1/s),�����������Ԫ��չ����
{
r
1
=
K
?
1
h
1
r
2
=
K
?
1
h
2
\left \{ \begin{aligned} \bold{r}_1=\bold{K}^{-1}\bold{h}_1 \\ \bold{r}_2=\bold{K}^{-1}\bold{h}_2 \end{aligned}\right.
{r1?=K?1h1?r2?=K?1h2??
��������ת�����������Ժ͵�λ��,���������
{
r
1
T
r
2
=
0
��
h
1
T
K
?
T
K
?
1
h
2
=
0
�O
�O
r
1
�O
�O
=
�O
�O
r
2
�O
�O
��
h
1
T
K
?
T
K
?
1
h
1
=
h
2
T
K
?
T
K
?
1
h
2
\left \{ \begin{aligned} \bold{r}_1^T\bold{r}_2 &= 0 \rightarrow \bold{h}_1^T\bold{K}^{-T}\bold{K}^{-1} \bold{h}_2 = 0 \\ ||\bold{r}_1||&=||\bold{r}_2|| \rightarrow \bold{h}_1^T\bold{K}^{-T}\bold{K}^{-1} \bold{h}_1= \bold{h}_2^T\bold{K}^{-T}\bold{K}^{-1} \bold{h}_2 \end{aligned}\right.
{r1T?r2?�O�Or1?�O�O?=0��h1T?K?TK?1h2?=0=�O�Or2?�O�O��h1T?K?TK?1h1?=h2T?K?TK?1h2??
������
B
=
K
?
T
K
?
1
\bold{B}=\bold{K}^{-T}\bold{K}^{-1}
B=K?TK?1,����
B
=
K
?
T
K
?
1
=
[
B
11
B
12
B
13
B
21
B
22
B
23
B
31
B
32
B
33
]
=
[
1
a
2
?
r
a
2
b
v
0
r
?
u
0
b
a
2
b
?
r
a
2
b
r
a
2
b
+
1
b
2
?
r
(
v
0
r
?
u
0
b
)
a
2
b
2
?
v
0
b
2
v
0
r
?
u
0
b
a
2
b
?
r
(
v
0
r
?
u
0
b
)
a
2
b
2
?
v
0
b
2
(
v
0
r
?
u
0
b
)
2
a
2
b
2
+
v
0
2
b
2
+
1
]
\bold{B}=\bold{K}^{-T}\bold{K}^{-1}= \begin{bmatrix} B_{11} & B_{12} &B_{13}\\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \end{bmatrix} = \\ \begin{bmatrix} \frac{1}{a^2} & -\frac{r}{a^2b} & \frac{v_0r-u_0b}{a^2b} \\ -\frac{r}{a^2b} & \frac{r}{a^2b}+\frac{1}{b^2} & -\frac{r(v_0r-u_0b)}{a^2b^2}-\frac{v_0}{b^2} \\ \frac{v_0r-u_0b}{a^2b} & -\frac{r(v_0r-u_0b)}{a^2b^2}-\frac{v_0}{b^2} & \frac{(v_0r-u_0b)^2}{a^2b^2}+\frac{v_0^2}{b^2}+1 \end{bmatrix}
B=K?TK?1=???B11?B21?B31??B12?B22?B32??B13?B23?B33?????=????a21??a2br?a2bv0?r?u0?b???a2br?a2br?+b21??a2b2r(v0?r?u0?b)??b2v0???a2bv0?r?u0?b??a2b2r(v0?r?u0?b)??b2v0??a2b2(v0?r?u0?b)2?+b2v02??+1?????
��ΪB�ǶԳƾ���,��˲���������
b
\bold{b}
bΪ:
b
=
[
B
11
,
B
12
,
B
22
,
B
13
,
B
23
,
B
33
]
T
\bold{b}=\begin{bmatrix} B_{11},B_{12},B_{22},B_{13},B_{23},B_{33} \end{bmatrix}^T
b=[B11?,B12?,B22?,B13?,B23?,B33??]T
���ڵ�Ӧ����H��������
h
i
\bold{h}_i
hi?,��:
h
i
=
[
h
i
1
,
h
i
2
,
h
i
3
]
T
\bold{h}_i=[h_{i1},h_{i2},h_{i3}]^T
hi?=[hi1?,hi2?,hi3?]T
��
b
b
b��
h
i
h_i
hi?���뵽��ת���������Լ����ȥ,�õ�:
h
i
T
B
h
j
=
m
i
j
T
b
=
0
\bold{h}_i^T\bold{B}\bold{h}_j=\bold{m}_{ij}^T\bold{b}=0
hiT?Bhj?=mijT?b=0
����,
m
i
j
=
[
h
i
1
h
j
1
,
h
i
1
h
j
2
+
h
i
2
h
j
1
,
h
i
2
h
j
2
,
h
i
3
h
j
1
+
h
i
1
h
j
3
,
h
i
3
h
j
2
+
h
i
2
h
j
3
,
h
i
3
h
j
3
]
T
\bold{m}_{ij}=[h_{i1}h_{j1},h_{i1}h_{j2}+h_{i2}h_{j1},h_{i2}h_{j2},h_{i3}h_{j1}+h_{i1}h_{j3},h_{i3}h_{j2}+h_{i2}h_{j3},h_{i3}h_{j3}]^T
mij?=[hi1?hj1?,hi1?hj2?+hi2?hj1?,hi2?hj2?,hi3?hj1?+hi1?hj3?,hi3?hj2?+hi2?hj3?,hi3?hj3?]T��
����,����Լ������дΪ��η���:
[
m
12
T
(
m
11
?
m
22
)
T
]
b
=
M
2
��
6
b
=
0
\begin{bmatrix} \bold{m}_{12}^T \\ (\bold{m}_{11}-\bold{m}_{22})^T \end{bmatrix} \bold{b}=\bold{M}_{2\times6}\bold{b}= \bold{0}
[m12T?(m11??m22?)T?]b=M2��6?b=0
M���ɵ�ӦH��������֪��,���ֻҪ����������̼��ɵõ�b������һ��ͼ��Ϳ��Եõ�2��Լ��,������÷���������Ҫ�ɼ�3��ͼ��,ʵ����,ͨ����ɼ�15-20�����ҡ�
�÷��̿���ʹ��SVD�������,�� M = U D V 6 �� 6 T \bold{M}=\bold{U}\bold{D}\bold{V}_{6\times6}^T M=UDV6��6T?,��V��D������ֵ�Ľ�������,ȡV�����һ�е���������Ϊ����b��
�����b�;���B��,���ɰ�(55)������
B
=
K
?
T
K
?
1
\bold{B}=\bold{K}^{-T}\bold{K}^{-1}
B=K?TK?1����ڲ�K:
v
0
=
(
B
12
B
13
?
B
11
B
23
)
/
(
B
11
B
22
?
B
12
2
)
��
=
B
33
?
[
B
13
2
+
v
0
(
B
12
B
13
?
B
11
B
23
)
]
/
B
11
a
=
��
/
B
11
b
=
��
B
11
/
(
B
11
B
22
?
B
12
2
)
r
=
?
B
12
a
2
b
/
��
u
0
=
r
v
0
/
a
?
B
13
a
2
/
��
\begin{aligned} v_0&=(B_{12}B_{13}-B_{11}B_{23})/(B_{11}B_{22}-B_{12}^2) \\ \lambda&=B_{33}-[B_{13}^2+v_0(B_{12}B_{13}-B_{11}B_{23})]/B_{11} \\ a&=\sqrt{\lambda/B_{11}} \\ b&=\sqrt{\lambda B_{11}/(B_{11}B_{22}-B_{12}^2)} \\ r&=-B_{12}a^2b/\lambda \\ u_0&=rv_0/a-B_{13}a^2/\lambda \end{aligned}
v0?��abru0??=(B12?B13??B11?B23?)/(B11?B22??B122?)=B33??[B132?+v0?(B12?B13??B11?B23?)]/B11?=��/B11??=��B11?/(B11?B22??B122?)?=?B12?a2b/��=rv0?/a?B13?a2/��?
��ο������ڲκ͵�Ӧ���:
r
1
=
��
K
?
1
h
1
r
2
=
��
K
?
1
h
2
r
1
=
r
1
��
r
2
t
=
��
K
?
1
h
3
\begin{aligned} \bold{r}_1=\lambda \bold{K}^{-1}\bold{h}_1 \\ \bold{r}_2=\lambda \bold{K}^{-1}\bold{h}_2 \\ \bold{r}_1=\bold{r}_{1}\times\bold{r}_2 \\ \bold{t}=\lambda \bold{K}^{-1}\bold{h}_3 \end{aligned}
r1?=��K?1h1?r2?=��K?1h2?r1?=r1?��r2?t=��K?1h3??
����,
��
=
1
/
�O
�O
K
?
1
h
1
�O
�O
=
1
/
�O
�O
K
?
1
h
2
�O
�O
\lambda=1/||\bold{K}^{-1}\bold{h}_1||=1/||\bold{K}^{-1}\bold{h}_2||
��=1/�O�OK?1h1?�O�O=1/�O�OK?1h2?�O�O,������������,�����������ת����R����һ�����㵥λ����������,��˿�����QR�ֽ�,���߽�����Ӿ���ռ���ͶӰ��SE(3)������:
R
=
(
R
R
T
)
?
1
/
2
R
\bold{R}=(\bold{R}\bold{R}^T)^{-1/2}\bold{R}
R=(RRT)?1/2R
�Ż���(���ǻ���)
֮ǰ�ı�ʽ�����û�п��ǻ���,������ǻ���Ҫ�Ա�ʽ���һ���Ż������Ƕ��忼���˻������ͶӰ���Ŀ�꺯��:
��
i
=
1
n
��
j
=
1
m
�O
�O
p
i
j
?
p
^
(
K
,
k
1
,
k
2
,
k
3
,
p
1
,
p
2
,
R
i
,
t
i
,
P
j
)
�O
�O
\sum_{i=1}^n\sum_{j=1}^m ||\bold{p}_{ij}-\bold{\hat{p}}(\bold{K},k_1,k_2,k_3,p_1,p_2,\bold{R_i},\bold{t_i},\bold{P}_j)||
i=1��n?j=1��m?�O�Opij??p^?(K,k1?,k2?,k3?,p1?,p2?,Ri?,ti?,Pj?)�O�O
����,��n��ͼ��,m��3D�㡣ͨ����С����Ŀ�꺯��,�������������ڲΡ����䡢��Ρ�
�����趨����εij�ʼֵ��Ϊ��ǰ��ñ�ʽ��,���������ʼΪ0������LM�㷨�����Ż�,����������IJ���,�������ı궨��