Dynamic Graph Convolutional Recurrent Network for Traffic Prediction: Benchmark and Solution
1. 文章概述
1.1 当前不足
- 交通图拓扑的动态特性需要进一步建模。预定义邻接矩阵和自适应邻接矩阵都是随时间变化的静态矩阵,不足以反映现实中路网拓扑的动态特性。
- 静态的基于距离的图和动态的基于属性的图从不同的角度描述了交通网络的拓扑结构,因此将它们结合起来可以为模型提供更大的范围来捕捉空间依赖关系。然而,大多数作品未能在保持效率和避免过度平滑的同时将它们融合在一起。
- 尽管在时间序列预测中得到广泛应用,但 RNN 及其变体的训练速度受到内部递归运算的限制,这阻碍了序列对序列等结构在流量预测任务中的应用
- 随着交通预测领域的快速发展,所提出的模型和交通数据集的数量也在不断增加,其中模型是在具有相应实验设置的不同数据集上进行评估的。这使得在模型之间进行公平的比较变得棘手,阻碍了该领域的发展。
1.2 主要贡献:
- 我们提出了一个基于GNN和RNN的模型,其中动态邻接矩阵被设计成从一个超网络逐步生成,与RNN迭代同步。
- 为了克服神经网络在效率和资源占用方面的不足,本文对基于RNN的模型采用了一种通用的训练方法,不仅有效地提高了性能,而且大大减少了训练时间消耗。
- 本文在三个公共数据集上进行了充分的比较实验,以获得各种复杂模型的公平比较结果,并得出一个可复制的标准化基准。该基准由15种代表性方法在3个数据集上的对比预测性能组成,可为研究者提供参考价值,促进相关问题的进一步研究。
1.3 相关研究
本文作者将相关工作按照空间拓扑构建、空间依赖建模、时间依赖建模和外部特征四个部分进行分类,如下表所示:
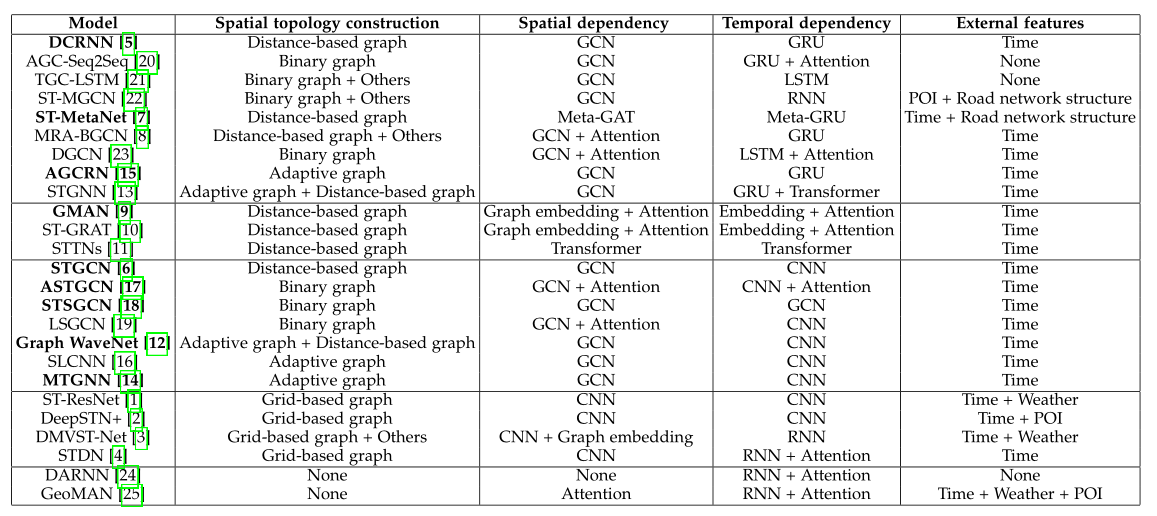
1.3.1 空间拓扑构建
预定义图:预定义的邻接矩阵是静态的,构造方法是有限的,这是描述复杂道路网络的天然缺陷
- 用阈值化的高斯核函数通过距离度量计算节点对之间的相似度,得到加权邻接矩阵或者仅仅使用连通性来导出一个简单的二进制邻接矩阵
- 多视图构图:像POI相似性,DTW相似性,自由流可达矩阵,边向图
自适应图:自适应图邻接矩阵的参数可以通过训练过程来学习,一些工作直接使邻接矩阵可学习,另一些工作计算可学习节点嵌入之间的相似性。然而,静态自适应邻接矩阵仍然很难建模道路网络的动态特性
1.3.2 空间相关性构建
- CNN被用于从欧式距离中获取空间相关性
- GCN在捕捉非欧几里德数据中的空间相关性方面是强大而灵活的
- 空间注意力
1.3.3 时间相关性构建
- RNN具有强大的捕捉时间相关性的能力,但是时间和内存的消耗大
- GRU、LSTM进一步提高了模型捕捉时间关系的能力且避免了梯度消失问题
- 注意力机制在序列依赖建模中也很强大
注意力机制存在问题:
1)受到内存消耗大和对计算资源要求高的限制
2)位置编码简单,不足以表示复杂的序列信息,自注意力只能导出重要性权重,因此捕捉局部(短期)序列相关性比RNNs更难。
1.3.4 外部特征
交通状况会受到天气,和POI,等外部因素的显著影响或推断,这些因素需要额外的收集和预处理。其他一些特征,如时间信息,DTW相似性,道路结构和连通性,可以从原始时间序列或邻接矩阵中生成
2.模型介绍
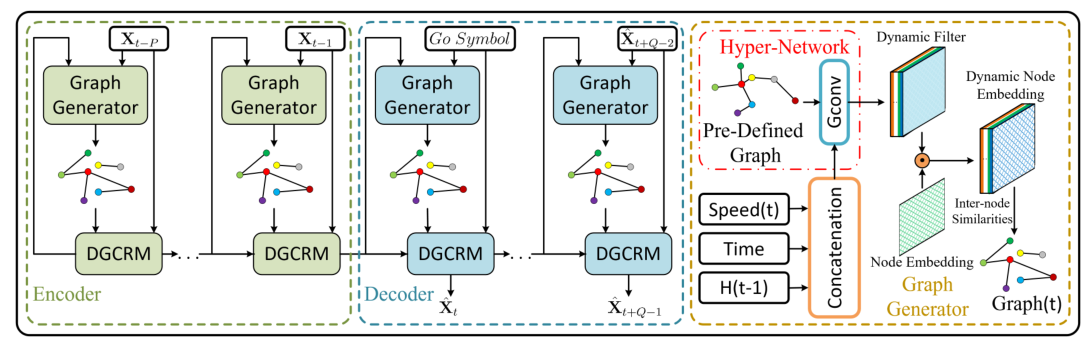
DGCRNN由两个主要部分组成:
- Graph generator:使用编码器和解码器的两个超网络来捕获动态信息并生成动态滤波器,然后将其与随机发起的节点嵌入向量相结合并生成动态节点嵌入。最后计算动态节点嵌入之间的成对相似度,并导出动态邻接矩阵
- Dynamic graph convolutional recurrent module:高效地集成动态图和静态图
| 变量 | 定义 |
|---|---|
| V t V_t Vt? | t时刻交通网络的速度 |
| T t T_t Tt? | 一天中的时刻t |
| H t H_{t} Ht??? | t时刻的隐藏状态 |
| A A A | 基于距离的邻接矩阵 |
2.1 Graph Generator
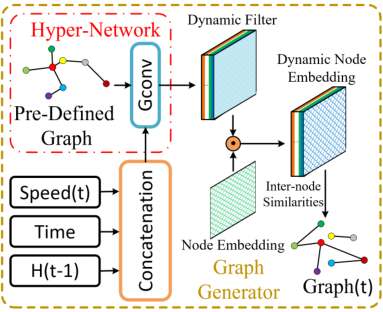
输入定义为:
I
t
=
V
t
∥
T
t
∥
H
t
?
1
I_t=V_t\|T_t\|H_{t-1}
It?=Vt?∥Tt?∥Ht?1?
其中
∥
\|
∥ 代表连接操作,对速度、时间、和隐藏状态的拼接作为图生成器的输入。本文使用hyper-network图卷积,通过基于距离的邻接矩阵A进行消息传递挖掘节点间的内在联系:
D
F
t
=
Θ
?
G
(
I
t
)
\mathbf{D F}^{t}=\Theta_{\star G}\left(\mathbf{I}_{t}\right)
DFt=Θ?G?(It?)
其输出为一个动态滤波器张量,在实际应用中本文作者使用了两个hyper-networks 去分别为源节点嵌入和目标节点嵌入生成两个动态过滤器,以此表达源节点的嵌入向量以及目标节点的嵌入向量,表示如下:
D
E
1
t
=
tanh
?
(
α
(
D
F
1
t
⊙
E
1
)
,
D
E
2
t
=
tanh
?
(
α
(
D
F
2
t
⊙
E
2
)
.
\mathbf{D E}_{1}^{t}=\tanh(\alpha(\mathbf{D F}_{1}^{t} \odot \mathbf{E}_{1}), \\ \mathbf{D E}_{2}^{t}=\tanh (\alpha(\mathbf{D F}_{2}^{t} \odot \mathbf{E}_{2}).
DE1t?=tanh(α(DF1t?⊙E1?),DE2t?=tanh(α(DF2t?⊙E2?).
其中
⊙
\odot
⊙表示哈达玛乘积,
α
\alpha
α为控制激活函数饱和速率的超参数。最后本文使用节点之间的相似性来计算动态邻接矩阵,如下所示
D
A
t
=
ReLU
?
(
tanh
?
(
α
(
D
E
1
t
D
E
2
t
T
?
D
E
2
t
D
E
1
t
T
)
)
)
\mathbf{D A}^{t}=\operatorname{ReLU}\left(\tanh \left(\alpha\left(\mathbf{D E}_{1}^{t} \mathbf{D} \mathbf{E}_{2}^{t^{T}}-\mathbf{D E}_{2}^{t} \mathbf{D} \mathbf{E}_{1}^{t^{T}}\right)\right)\right)
DAt=ReLU(tanh(α(DE1t?DE2tT??DE2t?DE1tT?)))
D
A
t
DA^t
DAt?为时间步长 t 的动态邻接矩阵。
? 总的来说,本文通过将RNN的隐藏状态添加到图生成的过程,并且在图生成过程中应用图卷积,使图生成变得更加有效,动态图的生成是对基于距离的静态邻接矩阵的补充。
2.2 Dynamic Graph Convolutional Recurrent Module
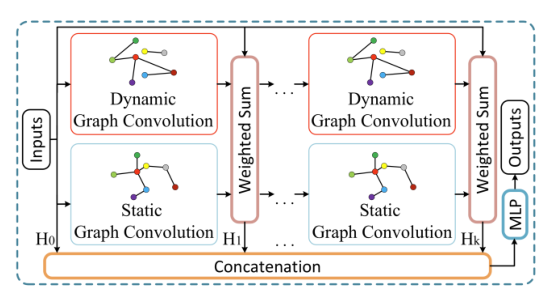
静态的基于距离的图和动态的基于节点属性的图从不同的角度反映了节间的相关性。本文在每个图卷积层上采用输入图信号、预定义静态图和动态图的图卷积结果的加权求和,k-hop动态图卷积模块可以表示如下:
H
(
k
)
=
α
H
i
n
+
β
H
(
k
?
1
)
D
A
t
+
γ
H
(
k
?
1
)
A
~
,
H
o
u
t
=
∑
i
=
0
K
H
(
k
)
W
(
k
)
,
H
(
0
)
=
H
i
n
D
A
t
=
D
~
t
?
1
(
D
A
t
+
I
)
D
~
:
,
i
,
i
t
=
1
+
∑
j
D
A
:
,
i
,
j
t
,
A
~
=
D
~
?
1
A
,
D
~
i
,
i
=
∑
j
A
i
,
j
\begin{aligned} &\mathbf{H}^{(k)}=\alpha \mathbf{H}_{i n}+\beta \mathbf{H}^{(k-1)} \mathbf{D} \mathbf{A}^{t}+\gamma \mathbf{H}^{(k-1)} \tilde{\mathbf{A}}, \\ &\mathbf{H}_{o u t}=\sum_{i=0}^{K} \mathbf{H}^{(k)} \mathbf{W}^{(k)}, \mathbf{H}^{(0)}=\mathbf{H}_{i n} \\ &\mathbf{D \mathbf { A }}^{t}=\tilde{\mathbf{D}}^{t^{-1}\left(\mathbf{D} \mathbf{A}^{t}+\mathbf{I}\right)} \\ &\tilde{\mathbf{D}}_{:, i, i}^{t}=1+\sum_{j} \mathbf{D} \mathbf{A}_{:, i, j}^{t}, \\ &\tilde{\mathbf{A}}=\tilde{\mathbf{D}}^{-1} \mathbf{A}, \tilde{\mathbf{D}}_{i, i}=\sum_{j} \mathbf{A}_{i, j} \end{aligned}
?H(k)=αHin?+βH(k?1)DAt+γH(k?1)A~,Hout?=i=0∑K?H(k)W(k),H(0)=Hin?DAt=D~t?1(DAt+I)D~:,i,it?=1+j∑?DA:,i,jt?,A~=D~?1A,D~i,i?=j∑?Ai,j??
本文采用双向图卷积来更好地利用有向图
H
o
=
Θ
1
?
G
(
H
i
n
,
D
A
t
,
A
)
+
Θ
2
?
G
(
H
i
n
,
D
A
t
T
,
A
T
)
\mathbf{H}_{o}=\Theta_{1 \star G}\left(\mathbf{H}_{i n}, \mathbf{D} \mathbf{A}^{t}, \mathbf{A}\right)+\Theta_{2 \star G}\left(\mathbf{H}_{i n}, \mathbf{D} \mathbf{A}^{t^{T}}, \mathbf{A}^{T}\right)
Ho?=Θ1?G?(Hin?,DAt,A)+Θ2?G?(Hin?,DAtT,AT)
RNN在建模顺序依赖方面很强大,GRU进一步提高了RNN在长期时间建模和避免梯度消失方面的能力。本文用动态图卷积模块代替GRU矩阵乘法,得到DGCRM,表示如下:
z
(
t
)
=
σ
(
Θ
z
?
G
(
X
t
∥
H
t
?
1
)
)
r
(
t
)
=
σ
(
Θ
r
?
G
(
X
t
∥
H
t
?
1
)
)
h
(
t
)
=
tanh
?
(
Θ
h
?
G
(
X
t
∥
(
r
(
t
)
⊙
H
t
?
1
)
)
)
H
t
=
z
(
t
)
⊙
H
t
?
1
+
(
1
?
z
(
t
)
)
⊙
h
(
t
)
\begin{aligned} z^{(t)} &=\sigma\left(\Theta_{z \star G}\left(\mathbf{X}_{t} \| \mathbf{H}_{t-1}\right)\right) \\ r^{(t)} &=\sigma\left(\Theta_{r \star G}\left(\mathbf{X}_{t} \| \mathbf{H}_{t-1}\right)\right) \\ h^{(t)} &=\tanh \left(\Theta_{h \star G}\left(\mathbf{X}_{t} \|\left(r^{(t)} \odot \mathbf{H}_{t-1}\right)\right)\right) \\ \mathbf{H}_{t} &=z^{(t)} \odot \mathbf{H}_{t-1}+\left(1-z^{(t)}\right) \odot h^{(t)} \end{aligned}
z(t)r(t)h(t)Ht??=σ(Θz?G?(Xt?∥Ht?1?))=σ(Θr?G?(Xt?∥Ht?1?))=tanh(Θh?G?(Xt?∥(r(t)⊙Ht?1?)))=z(t)⊙Ht?1?+(1?z(t))⊙h(t)?
2.3 训练策略
本文在RNN正向传播过程中,并不是直接计算解码器的所有步骤,而只计算前i个步骤。随着训练过程的进行,不断增加,直到它达到最大值,也就是预测序列的长度。这样,模型就不需要在训练过程中一直采用前向和后向传播,这可以显著减少时间消耗,并在早期节省GPU内存。更重要的是,由于早期时间步骤的良好基础,绩效也可以从策略中受益。