数据分为训练数据/监督数据(优化)和测试数据(评价泛化能力)。
(1)优化(optimization):用模型拟合观测数据的过程;
(2)泛化(generalization):数学原理和实践者的智慧,能够指导我们生成出有效性超出用于训练的数据集本身的模型。
损失函数(loss function) yk,tk(one-hot:正解1 其余0)
均方误差(mean squared error)
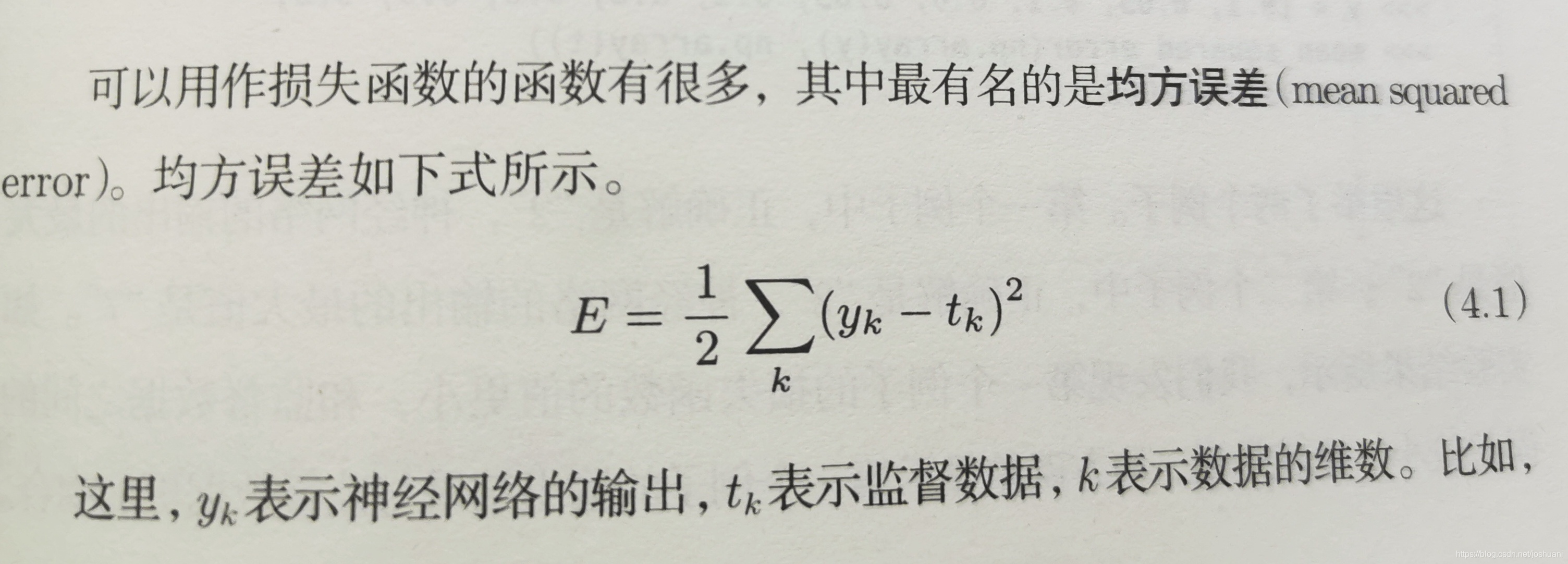


交叉熵误差(cross entropy error)


mini-batch学习 和chapter3 batch区分
1.在学习过程中,要对所有数据求损失函数,并求平均值。
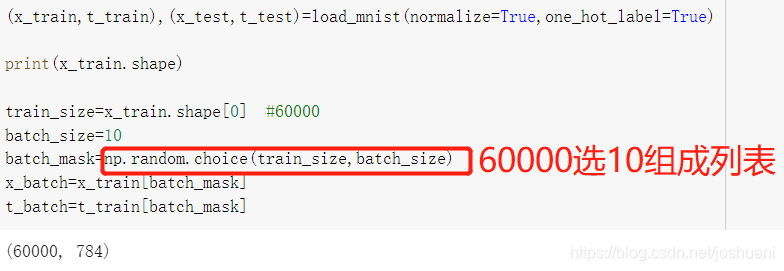
2.但数据量可能很大,所以选一个mini-batch代表所有数据,求其损失函数。
3.Chapter3中的batch是优化过程中把所有训练数据分批训练,强调分批比一个一个更快。
而本章的mini-batch学习是直接抽一部分学,强调如果全学损失函数计算太复杂。
mini-batch版交叉熵误差的实现
适用于单个数据+批量数据

数值微分(numerical differentiation)
利用微小的差分求导数的过程叫数值微分。
导数的定义式是前向差分
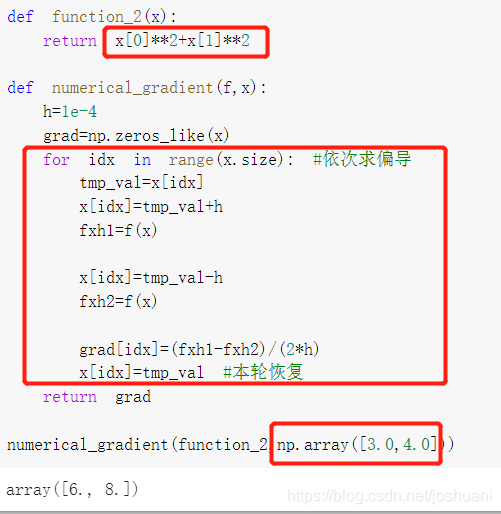
而编程实现采用中心差分

偏导数 略
梯度下降法
方法
求梯度->沿着梯度走一段距离(更新参数)->求新梯度->再沿新梯度走一段距离…
性质
梯度下降法寻找的是梯度为0的点。
负梯度指向函数值减小最快的方向,但并非指向最小值处。
梯度为0的点:极小值、最小值、鞍点(某个方向看是最大值,另个方向看是极小值)
鞍点:

梯度的实现
参数x是Numpy数组
数学式 学习率(learning rate)η

学习率过大或者过小都不能得到好的结果
学习率这样的超参数需要人工设定
实现
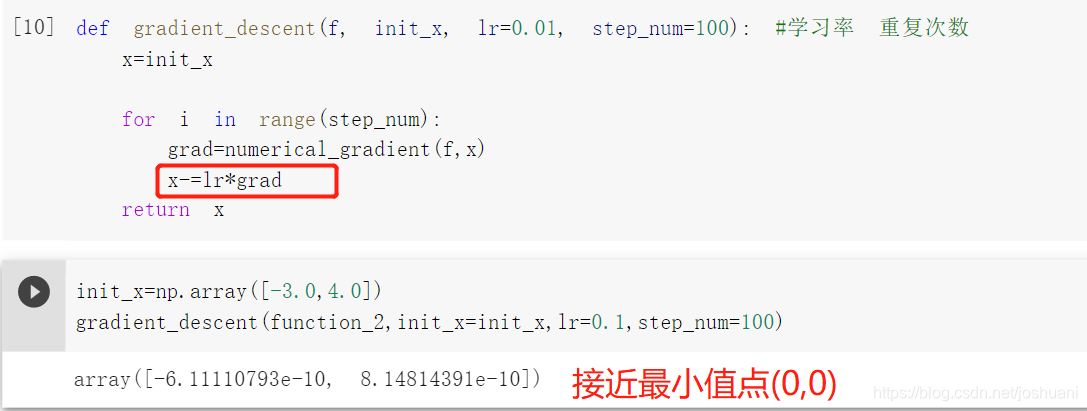
神经网络的梯度

学习算法的实现
以两层神经网络,使用MNIST学习。
步骤:
1.mini-batch
2.计算梯度
3.更新参数
4.重复
因为mini-batch,所以称为随机梯度下降法(SGD:stochastic graident descent)
λ表达式
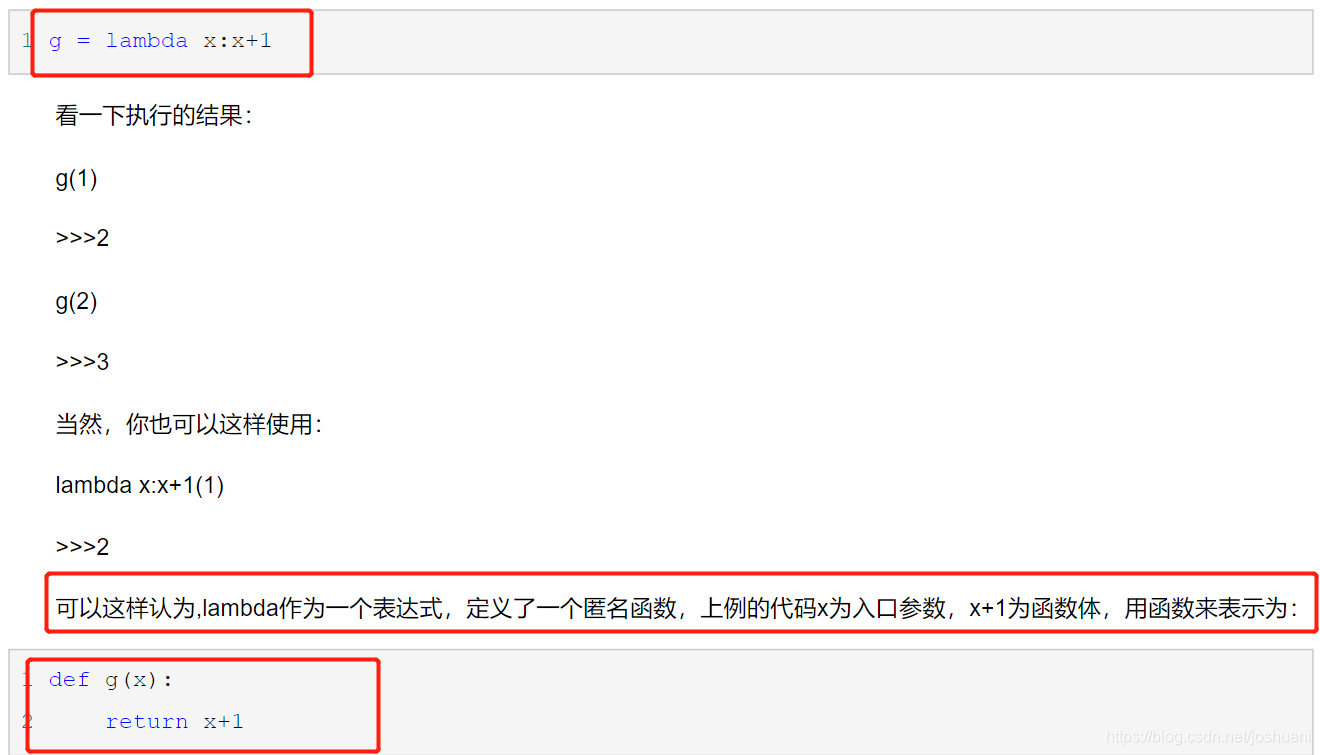
实现:两层神经网络的类


实现:mini-batch学习
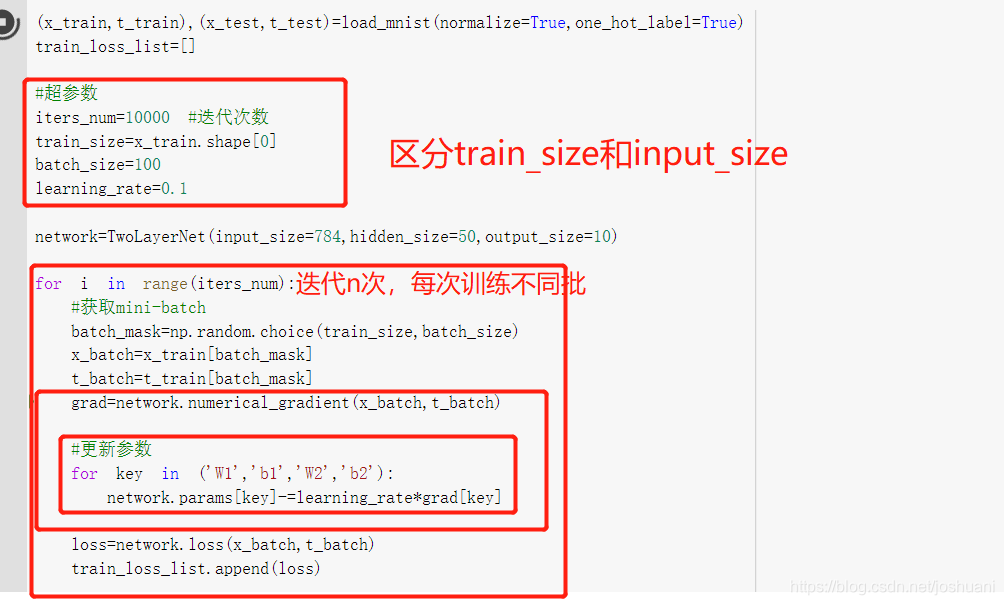
进一步优化:基于测试数据的评价
需确认是否发生过拟合
过拟合(overfitting):训练数据中的数字图像能被辨别,但不在训练数据中的图像无法被辨别。即泛化能力差。
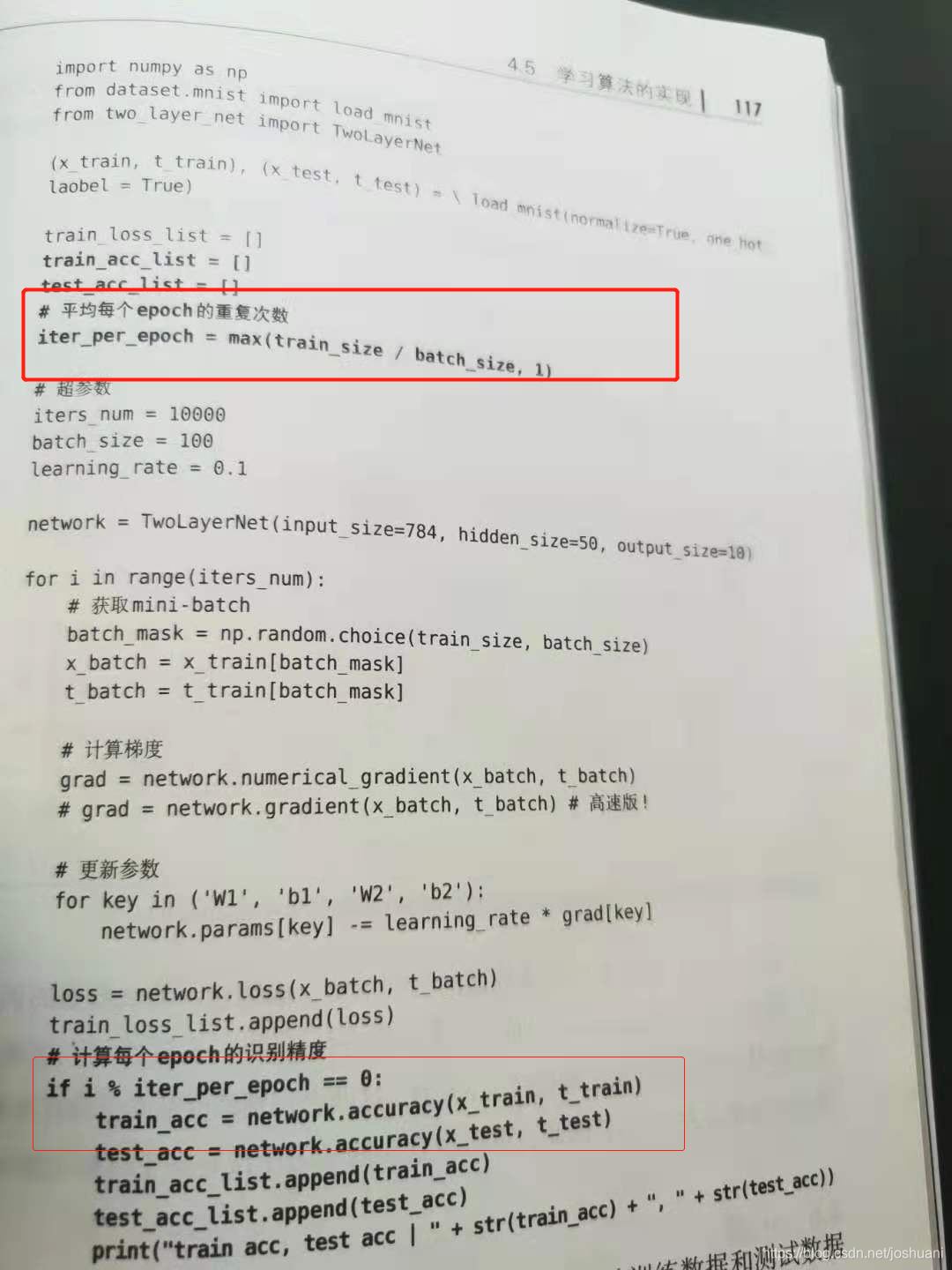
评价方法:每一个epoch记录下训练数据和测试数据的识别精度
epoch:一个epoch表示所有训练数据都被使用过一次时的更新次数。
10000笔训练数据,随机打乱后按100/批依次分,则训练100次即可训练所有数据,100次就是一个epoch。