Pytorch CIFAR10图像分类 LeNet5篇
文章目录
这里贴一下汇总篇: 汇总篇
4.定义网络(LeNet5)
手写字体识别模型LeNet5诞生于1994年,是最早的卷积神经网络之一。LeNet5通过巧妙的设计,利用卷积、参数共享、池化等操作提取特征,避免了大量的计算成本,最后再使用全连接神经网络进行分类识别,这个网络也是最近大量神经网络架构的起点。
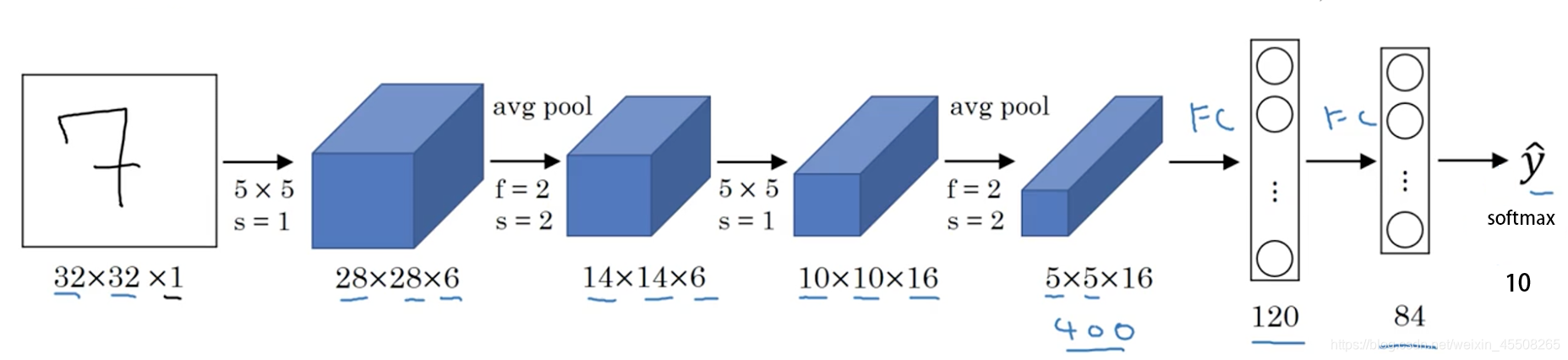
LeNet-5 一些性质:
-
如果输入层不算神经网络的层数,那么 LeNet-5 是一个 7 层的网络。(有些地方也可能把 卷积和池化 当作一个 layer)(LeNet-5 名字中的“5”也可以理解为整个网络中含可训练参数的层数为 5。)
-
LeNet-5 大约有 60,000 个参数。
-
随着网络越来越深,图像的高度和宽度在缩小,与此同时,图像的 channel 数量一直在增加。
-
现在常用的 LeNet-5 结构和 Yann LeCun 教授在 1998 年论文中提出的结构在某些地方有区别,比如激活函数的使用,现在一般使用 ReLU 作为激活函数,输出层一般选择 softmax。
首先我们还是得判断是否可以利用GPU,因为GPU的速度可能会比我们用CPU的速度快20-50倍左右,特别是对卷积神经网络来说,更是提升特别明显。
device = 'cuda' if torch.cuda.is_available() else 'cpu'
#定义网络
class LeNet5(nn.Module):# nn.Module是所有神经网络的基类,我们自己定义任何神经网络,都要继承nn.Module
def __init__(self):
super(LeNet5,self).__init__()
self.conv1 = nn.Sequential(
# 卷积层1,3通道输入,6个卷积核,核大小5*5
# 经过该层图像大小变为32-5+1,28*28
nn.Conv2d(in_channels=3,out_channels=6,kernel_size=5,stride=1, padding=0),
#激活函数
nn.ReLU(),
# 经2*2最大池化,图像变为14*14
nn.MaxPool2d(kernel_size=2,stride=2,padding=0),
)
self.conv2 = nn.Sequential(
# 卷积层2,6输入通道,16个卷积核,核大小5*5
# 经过该层图像变为14-5+1,10*10
nn.Conv2d(in_channels=6,out_channels=16,kernel_size=5,stride=1, padding=0),
nn.ReLU(),
# 经2*2最大池化,图像变为5*5
nn.MaxPool2d(kernel_size=2,stride=2,padding=0),
)
self.fc = nn.Sequential(
# 接着三个全连接层
nn.Linear(16*5*5,120),
nn.ReLU(),
nn.Linear(120,84),
nn.ReLU(),
nn.Linear(84,10),
)
# 定义前向传播过程,输入为
def forward(self,x):
x = self.conv1(x)
x = self.conv2(x)
# nn.Linear()的输入输出都是维度为一的值,所以要把多维度的tensor展平成一维
x = x.view(x.size()[0],-1)
x = self.fc(x)
return x
net = LeNet5().cuda()
summary(net,(3,32,32))
---------------------------------------------------------------- Layer (type) Output Shape Param # ================================================================ Conv2d-1 [-1, 6, 28, 28] 456 ReLU-2 [-1, 6, 28, 28] 0 MaxPool2d-3 [-1, 6, 14, 14] 0 Conv2d-4 [-1, 16, 10, 10] 2,416 ReLU-5 [-1, 16, 10, 10] 0 MaxPool2d-6 [-1, 16, 5, 5] 0 Linear-7 [-1, 120] 48,120 ReLU-8 [-1, 120] 0 Linear-9 [-1, 84] 10,164 ReLU-10 [-1, 84] 0 Linear-11 [-1, 10] 850 ================================================================ Total params: 62,006 Trainable params: 62,006 Non-trainable params: 0 ---------------------------------------------------------------- Input size (MB): 0.01 Forward/backward pass size (MB): 0.11 Params size (MB): 0.24 Estimated Total Size (MB): 0.36 ----------------------------------------------------------------
首先从我们summary可以看到,我们定义的模型的参数大概是62 thousands,我们输入的是(batch,3,32,32)的张量,并且这里也能看到每一层后我们的图像输出大小的变化,最后输出10个参数,再通过softmax函数就可以得到我们每个类别的概率了。
我们也可以打印出我们的模型观察一下
LeNet5(
(conv1): Sequential(
(0): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(conv2): Sequential(
(0): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(fc): Sequential(
(0): Linear(in_features=400, out_features=120, bias=True)
(1): ReLU()
(2): Linear(in_features=120, out_features=84, bias=True)
(3): ReLU()
(4): Linear(in_features=84, out_features=10, bias=True)
)
)
如果你的电脑有多个GPU,这段代码可以利用GPU进行并行计算,加快运算速度
net =LeNet5().to(device)
if device == 'cuda':
net = nn.DataParallel(net)
# 当计算图不会改变的时候(每次输入形状相同,模型不改变)的情况下可以提高性能,反之则降低性能
torch.backends.cudnn.benchmark = True
5. 定义损失函数和优化器
pytorch将深度学习中常用的优化方法全部封装在torch.optim之中,所有的优化方法都是继承基类optim.Optimizier
损失函数是封装在神经网络工具箱nn中的,包含很多损失函数
这里我使用的是SGD + momentum算法,并且我们损失函数定义为交叉熵函数,除此之外学习策略定义为动态更新学习率,如果5次迭代后,训练的损失并没有下降,那么我们便会更改学习率,会变为原来的0.5倍,最小降低到0.00001
如果想更加了解优化器和学习率策略的话,可以参考以下资料
- Pytorch Note15 优化算法1 梯度下降(Gradient descent varients)
- Pytorch Note16 优化算法2 动量法(Momentum)
- Pytorch Note34 学习率衰减
这里决定迭代20次
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=1e-1, momentum=0.9, weight_decay=5e-4)
criterion = nn.CrossEntropyLoss()
scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', factor=0.5 ,patience = 5,min_lr = 0.000001) # 动态更新学习率
# scheduler = optim.lr_scheduler.MultiStepLR(optimizer, milestones=[75, 150], gamma=0.5)
import time
epoch = 20
6. 训练
首先定义模型保存的位置
import os
if not os.path.exists('./model'):
os.makedirs('./model')
else:
print('文件已存在')
save_path = './model/LeNet5.pth'
我定义了一个train函数,在train函数中进行一个训练,并保存我们训练后的模型
from utils import trainfrom utils import plot_historyAcc, Loss, Lr = train(net, trainloader, testloader, epoch, optimizer, criterion, scheduler, save_path, verbose = True)
Epoch [ 1/ 20] Train Loss:1.918313 Train Acc:28.19% Test Loss:1.647650 Test Acc:39.23% Learning Rate:0.100000 Time 00:29Epoch [ 2/ 20] Train Loss:1.574629 Train Acc:42.00% Test Loss:1.521759 Test Acc:44.59% Learning Rate:0.100000 Time 00:21Epoch [ 3/ 20] Train Loss:1.476749 Train Acc:46.23% Test Loss:1.438898 Test Acc:48.56% Learning Rate:0.100000 Time 00:21Epoch [ 4/ 20] Train Loss:1.415963 Train Acc:49.10% Test Loss:1.378597 Test Acc:50.25% Learning Rate:0.100000 Time 00:21Epoch [ 5/ 20] Train Loss:1.384430 Train Acc:50.69% Test Loss:1.350369 Test Acc:51.81% Learning Rate:0.100000 Time 00:20Epoch [ 6/ 20] Train Loss:1.331118 Train Acc:52.49% Test Loss:1.384710 Test Acc:49.62% Learning Rate:0.100000 Time 00:20Epoch [ 7/ 20] Train Loss:1.323763 Train Acc:53.08% Test Loss:1.348911 Test Acc:52.59% Learning Rate:0.100000 Time 00:21Epoch [ 8/ 20] Train Loss:1.291410 Train Acc:54.19% Test Loss:1.273263 Test Acc:55.00% Learning Rate:0.100000 Time 00:20Epoch [ 9/ 20] Train Loss:1.261590 Train Acc:55.36% Test Loss:1.295092 Test Acc:54.50% Learning Rate:0.100000 Time 00:20Epoch [ 10/ 20] Train Loss:1.239585 Train Acc:56.45% Test Loss:1.349028 Test Acc:52.57% Learning Rate:0.100000 Time 00:21Epoch [ 11/ 20] Train Loss:1.225227 Train Acc:56.81% Test Loss:1.293521 Test Acc:53.87% Learning Rate:0.100000 Time 00:22Epoch [ 12/ 20] Train Loss:1.221355 Train Acc:56.86% Test Loss:1.255155 Test Acc:56.13% Learning Rate:0.100000 Time 00:21Epoch [ 13/ 20] Train Loss:1.207748 Train Acc:57.59% Test Loss:1.238375 Test Acc:57.10% Learning Rate:0.100000 Time 00:21Epoch [ 14/ 20] Train Loss:1.195587 Train Acc:58.01% Test Loss:1.185524 Test Acc:58.56% Learning Rate:0.100000 Time 00:20Epoch [ 15/ 20] Train Loss:1.183456 Train Acc:58.50% Test Loss:1.192770 Test Acc:58.04% Learning Rate:0.100000 Time 00:21Epoch [ 16/ 20] Train Loss:1.168697 Train Acc:59.13% Test Loss:1.272912 Test Acc:55.85% Learning Rate:0.100000 Time 00:20Epoch [ 17/ 20] Train Loss:1.167685 Train Acc:59.23% Test Loss:1.195087 Test Acc:58.33% Learning Rate:0.100000 Time 00:20Epoch [ 18/ 20] Train Loss:1.162324 Train Acc:59.37% Test Loss:1.242964 Test Acc:56.62% Learning Rate:0.100000 Time 00:21Epoch [ 19/ 20] Train Loss:1.154494 Train Acc:59.72% Test Loss:1.274993 Test Acc:54.90% Learning Rate:0.100000 Time 00:21Epoch [ 20/ 20] Train Loss:1.163650 Train Acc:59.45% Test Loss:1.182077 Test Acc:59.00% Learning Rate:0.100000 Time 00:20
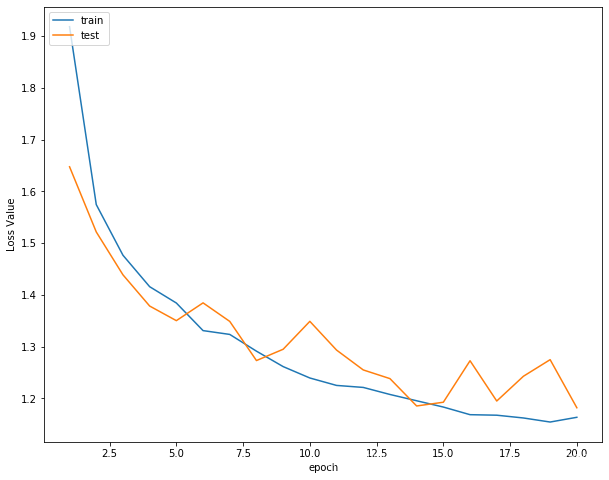
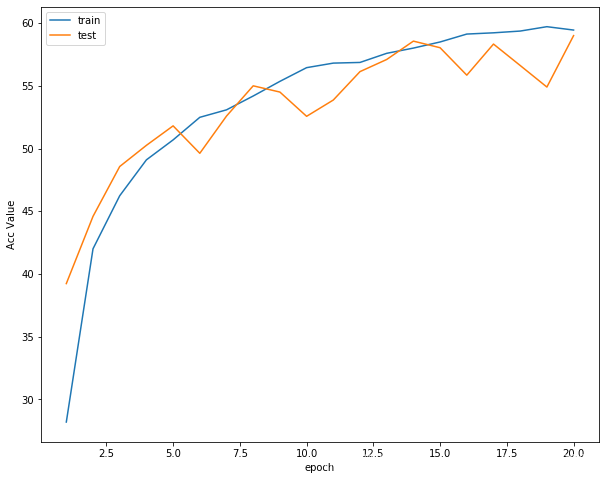
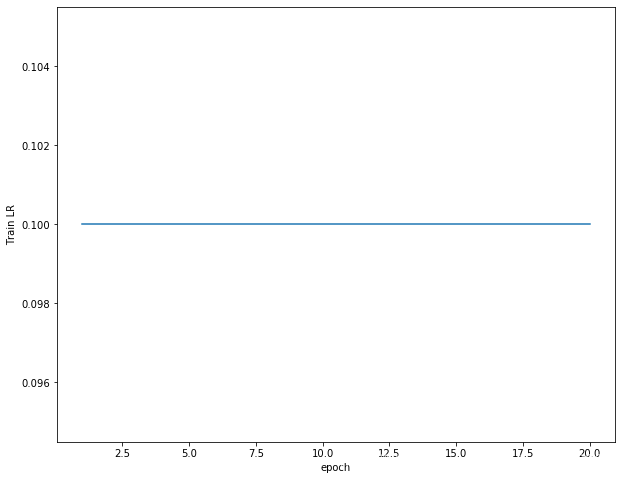
接着可以分别打印,损失函数曲线,准确率曲线和学习率曲线
plot_history(epoch ,Acc, Loss, Lr)
损失函数曲线
准确率曲线
学习率曲线
7.测试
查看准确率
correct = 0 # 定义预测正确的图片数,初始化为0
total = 0 # 总共参与测试的图片数,也初始化为0
# testloader = torch.utils.data.DataLoader(testset, batch_size=32,shuffle=True, num_workers=2)
for data in testloader: # 循环每一个batch
images, labels = data
images = images.to(device)
labels = labels.to(device)
net.eval() # 把模型转为test模式
if hasattr(torch.cuda, 'empty_cache'):
torch.cuda.empty_cache()
outputs = net(images) # 输入网络进行测试
# outputs.data是一个4x10张量,将每一行的最大的那一列的值和序号各自组成一个一维张量返回,第一个是值的张量,第二个是序号的张量。
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0) # 更新测试图片的数量
correct += (predicted == labels).sum() # 更新正确分类的图片的数量
print('Accuracy of the network on the 10000 test images: %.2f %%' % (100 * correct / total))
Accuracy of the network on the 10000 test images: 59.31 %
可以看到自定义网络的模型在测试集中准确率达到59.31%
程序中的 torch.max(outputs.data, 1) ,返回一个tuple (元组)
而这里很明显,这个返回的元组的第一个元素是image data,即是最大的 值,第二个元素是label, 即是最大的值 的 索引!我们只需要label(最大值的索引),所以就会有_,predicted这样的赋值语句,表示忽略第一个返回值,把它赋值给_, 就是舍弃它的意思;
查看每一类的准确率
# 定义2个存储每类中测试正确的个数的 列表,初始化为0
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
# testloader = torch.utils.data.DataLoader(testset, batch_size=64,shuffle=True, num_workers=2)
net.eval()
with torch.no_grad():
for data in testloader:
images, labels = data
images = images.to(device)
labels = labels.to(device)
if hasattr(torch.cuda, 'empty_cache'):
torch.cuda.empty_cache()
outputs = net(images)
_, predicted = torch.max(outputs.data, 1)
#4组(batch_size)数据中,输出于label相同的,标记为1,否则为0
c = (predicted == labels).squeeze()
for i in range(len(images)): # 因为每个batch都有4张图片,所以还需要一个4的小循环
label = labels[i] # 对各个类的进行各自累加
class_correct[label] += c[i]
class_total[label] += 1
for i in range(10):
print('Accuracy of %5s : %.2f %%' % (classes[i], 100 * class_correct[i] / class_total[i]))
Accuracy of airplane : 70.80 % Accuracy of automobile : 68.30 % Accuracy of bird : 36.70 % Accuracy of cat : 35.80 % Accuracy of deer : 56.90 % Accuracy of dog : 40.00 % Accuracy of frog : 79.70 % Accuracy of horse : 66.30 % Accuracy of ship : 58.10 % Accuracy of truck : 80.10 %
抽样测试并可视化一部分结果
dataiter = iter(testloader)
images, labels = dataiter.next()
images_ = images
#images_ = images_.view(images.shape[0], -1)
images_ = images_.to(device)
labels = labels.to(device)
val_output = net(images_)
_, val_preds = torch.max(val_output, 1)
fig = plt.figure(figsize=(25,4))
correct = torch.sum(val_preds == labels.data).item()
val_preds = val_preds.cpu()
labels = labels.cpu()
print("Accuracy Rate = {}%".format(correct/len(images) * 100))
fig = plt.figure(figsize=(25,25))
for idx in np.arange(64):
ax = fig.add_subplot(8, 8, idx+1, xticks=[], yticks=[])
#fig.tight_layout()
# plt.imshow(im_convert(images[idx]))
imshow(images[idx])
ax.set_title("{}, ({})".format(classes[val_preds[idx].item()], classes[labels[idx].item()]),
color = ("green" if val_preds[idx].item()==labels[idx].item() else "red"))
Accuracy Rate = 58.59375% <Figure size 1800x288 with 0 Axes>

8. 保存模型
torch.save(net,save_path[:-4]+'_'+str(epoch)+'.pth')
# torch.save(net, './model/MyNet.pth')
9. 预测
读取本地图片进行预测
import torch
from PIL import Image
from torch.autograd import Variable
import torch.nn.functional as F
from torchvision import datasets, transforms
import numpy as np
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Mynet()
model = torch.load(save_path) # 加载模型
# model = model.to('cuda')
model.eval() # 把模型转为test模式
# 读取要预测的图片
img = Image.open("./airplane.jpg").convert('RGB') # 读取图像
img

接着我们就进行预测图片,不过这里有一个点,我们需要对我们的图片也进行transforms,因为我们的训练的时候,对每个图像也是进行了transforms的,所以我们需要保持一致
trans = transforms.Compose([transforms.Scale((32,32)),
transforms.ToTensor(),
transforms.Normalize(mean=(0.5, 0.5, 0.5),
std=(0.5, 0.5, 0.5)),
])
img = trans(img)
img = img.to(device)
# 图片扩展多一维,因为输入到保存的模型中是4维的[batch_size,通道,长,宽],而普通图片只有三维,[通道,长,宽]
img = img.unsqueeze(0)
# 扩展后,为[1,3,32,32]
output = model(img)
prob = F.softmax(output,dim=1) #prob是10个分类的概率
print("概率",prob)
value, predicted = torch.max(output.data, 1)
print("类别",predicted.item())
print(value)
pred_class = classes[predicted.item()]
print("分类",pred_class)
概率 tensor([[8.6320e-01, 1.7801e-04, 3.6034e-03, 3.1733e-04, 2.0015e-03, 6.3802e-05, 6.5461e-05, 2.0457e-04, 1.2603e-01, 4.3343e-03]], device='cuda:0', grad_fn=<SoftmaxBackward>) 类别 0 tensor([6.2719], device='cuda:0') 分类 plane
这里就可以看到,我们最后的结果,分类为plane,我们的置信率大概是86.32%
读取图片地址进行预测
我们也可以通过读取图片的url地址进行预测,这里我找了多个不同的图片进行预测
import requests
from PIL import Image
url = 'https://dss2.bdstatic.com/70cFvnSh_Q1YnxGkpoWK1HF6hhy/it/u=947072664,3925280208&fm=26&gp=0.jpg'
url = 'https://ss0.bdstatic.com/70cFuHSh_Q1YnxGkpoWK1HF6hhy/it/u=2952045457,215279295&fm=26&gp=0.jpg'
url = 'https://ss0.bdstatic.com/70cFvHSh_Q1YnxGkpoWK1HF6hhy/it/u=2838383012,1815030248&fm=26&gp=0.jpg'
url = 'https://gimg2.baidu.com/image_search/src=http%3A%2F%2Fwww.goupuzi.com%2Fnewatt%2FMon_1809%2F1_179223_7463b117c8a2c76.jpg&refer=http%3A%2F%2Fwww.goupuzi.com&app=2002&size=f9999,10000&q=a80&n=0&g=0n&fmt=jpeg?sec=1624346733&t=36ba18326a1e010737f530976201326d'
url = 'https://ss3.bdstatic.com/70cFv8Sh_Q1YnxGkpoWK1HF6hhy/it/u=2799543344,3604342295&fm=224&gp=0.jpg'
# url = 'https://ss1.bdstatic.com/70cFuXSh_Q1YnxGkpoWK1HF6hhy/it/u=2032505694,2851387785&fm=26&gp=0.jpg'
response = requests.get(url, stream=True)
print (response)
img = Image.open(response.raw)
img

这里和前面是一样的
trans = transforms.Compose([transforms.Scale((32,32)),
transforms.ToTensor(),
transforms.Normalize(mean=(0.5, 0.5, 0.5),
std=(0.5, 0.5, 0.5)),
])
img = trans(img)
img = img.to(device)
# 图片扩展多一维,因为输入到保存的模型中是4维的[batch_size,通道,长,宽],而普通图片只有三维,[通道,长,宽]
img = img.unsqueeze(0)
# 扩展后,为[1,3,32,32]
output = model(img)
prob = F.softmax(output,dim=1) #prob是10个分类的概率
print("概率",prob)
value, predicted = torch.max(output.data, 1)
print("类别",predicted.item())
print(value)
pred_class = classes[predicted.item()]
print("分类",pred_class)
概率 tensor([[0.7491, 0.0015, 0.0962, 0.0186, 0.0605, 0.0155, 0.0025, 0.0150, 0.0380, 0.0031]], device='cuda:0', grad_fn=<SoftmaxBackward>) 类别 0 tensor([3.6723], device='cuda:0') 分类 plane
可以看到,我们分类的结果是plane,而真正的分类是cat,所以这个模型还不是特别完美,还需要不断完善
10.总结
其实对于我们的LeNet5来说,这个模型最先出现是在MINST数据集上达到了很高的准确率,最早使用邮票上的数字识别。从实验结果可以看得出来,他其实对CIFAR10的分类并没有表现的很好,所以如果想用LeNet5进行图像识别,要多考虑一下
顺带提一句,我们的数据和代码都在我的汇总篇里有说明,如果需要,可以自取
这里再贴一下汇总篇:汇总篇
